On a Constitutive Material Model to Capture Time Dependent Behavior of Cortical Bone ()
1. Introduction
The main function of bone is to carry load. An external load applied to bone induces strains of different magnitudes, depending on loading condition, geometry and material behavior of the bone. Numerous investigations have been conducted to examine the behavior of bone under loading [1] - [14] . Research has found that when cor- tical bone is loaded below yield load, the initial mechanical response is linear and can be described by Hooke’s law. Bone constitutes a hierarchical structure, where all structural levels determine the macro material properties [15] [16] and contains of three major components, collagen, mineral and body fluid, that contribute to the me- chanical behavior. Currey [17] finds that Young’s modulus is correlated to the amount of hydroxyapatite, where increased content of the mineral results in higher Young’s modulus. If the load is increased, the bone reaches a yield point with an associated yield strain. Currey [17] further finds that bone seems to yield at a particular strain level of 0.0036 - 0.012 rather than at a particular stress level, with lower strain values for high Young’s modulus and high mineral content. Several researchers have found that bone exhibits viscoelastic properties both in tension and compression [1] [2] [4] [18] - [21] . In these studies the material stiffness represented by Young’s modulus increased with increased strain rate but for the yield strain the results were not coherent. The results of Crowninshield and Pope [4] indicate that higher strain rate gives higher yield strain in tension. Similar findings were obtained by Currey [22] and Melnis and Knets [18] . However the results of compression test by McElhaney [1] indicate that for low strain rate, the yield strain level is independent of strain rate but decreases for high strain rates. Hansen et al. [20] reported decreased yield strain levels for increased strain rate in tension. This contradiction in results may reflect different species, specimen sampling, specimen preparation and testing procedures. Currey [23] finds that the homogenized bone properties are species specific. Melnis and Knets [18] conclude that the mechanical properties and viscoelastic behavior of bone material are significantly dependent on moisture content. It has also been found that the age of the bone affects its porosity which in turn affects the mechanical properties such as ultimate stress, ultimate strain, and yield stress [24] . Beyond the yield strain, post yield strain occurs in the bone. Post yield strain reflects damage of the material caused by micro cracks and/or internal slip between the mineral and collagen that degrades the material until failure [13] [25] . Studies have demonstrated that the strain rate affects the evolution of post yield strain, where lower strain rate exhibits an in- crease of post yield strain before failure [1] [4] [25] . Beyond yield strain, bone may withstand increased loading due to hardening before failure [1] [4] [18] . It has also been found that bone demonstrates relaxation over time [26] . According to Iyo et al. [26] the relaxation phenomena consists of two different processes: one fast process (relaxation time in order of 102 s) explained by relaxation of the collagen matrix and one slower relaxation (re- laxation time in order of 106 s) related to the higher order structure of the bone. Several studies have shown that bone exhibits creep phenomena including a viscoelastic creep that recovers after unloading and a creep that re- mains after unloading [27] - [30] . Bone is a living material and it is difficult to perform strength tests in vivo. Therefore most studies have been performed in vitro on dead bone. However a few in vivo tests exist that can be used to extract the mechanical properties of bone [8] [31] [32] . Perren et al. [8] installed compression plates in sheep tibia in vivo and measured the development of longitudinal forces over time. They concluded that an ini- tial decrease in axial force is related to the viscoelastic properties of bone and that a subsequent linear decrease in pressure is related to remodeling. Similar findings have been reported by Cordey et al. [32] and by Blumlein et al. [31] . Generally the remodeling rate is species dependent [33] . To capture the behavior of cortical bone subjected to various loading rate it is essential to have a constitutive material model that captures the stress- strain relationship for different strain rates. Johnson et al. [11] developed a viscoelastic-viscoplastic constitutive model that describes the stress-strain relationship for different strain rates. Their model demonstrates excellent agreement with published experimental tests results. However the Johnson et al. [11] model does not contain a remodeling term for biological reduction of the initiated pre-stress over time. In addition it does neither model relaxation nor creep. Furthermore, it does not reflect the hardening effect implying that the stress may increase during post yield strain. When an oversized implant is inserted into bone it induces static strains that create static stresses in the bone that gradually decline due to relaxation and remodeling. In addition, if a constant load is ap- plied strains increase in time due to creep. The objective of the present study is to develop a constitutive model for cortical bone that captures the mechanical behavior of the bone subjected to a longitudinal load. The pro- posed constitutive model with calibrated model parameters should predict the stress strain, relaxation and creep behavior observed in the in vivo and in vitro experiments.
2. Theory
This work proposes a viscoelastic-viscoplastic material model with a remodeling term to describe the relationship between stress and strain in vivo. This model has similarities to that of Johnson et al. [11] but also captures hardening, relaxation, creep and remodeling behavior. The model is illustrated by the rheological model according to Figure 1.
It consists of three different components: one viscoelastic, one viscoplastic, and one remodeling component. The individual components might contain several parts, contributing to the specific behavior of bone.
The total strain according to Figure 1 can be defined as follows:
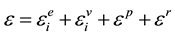 (1)
(1)
The parameters describing the material model (Table 1) are calibrated by use of experimental results, representing homogenized bone, found in the literature (Table 2).
The relationship between stress and strain for each component, respectively, is derived by the use of the dissipation inequality according to the second law of thermodynamics.
2.1. Viscoelastic component
During function, short term loads with different loading rates are applied which affect the bone differently due to the viscoelastic properties. To predict viscoelastic creep, relaxation and stiffness for different strain rates the proposed model consists of one spring element and four Maxwell elements in parallel (Figure 1).
The strain rate 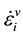 in the individual dashpot
in the individual dashpot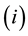 , of the Maxwell element, with associated viscosity
, of the Maxwell element, with associated viscosity 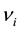 is defined as:
is defined as:
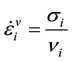 (2)
(2)
2.2. Viscoplastic component
The viscoplastic component contains a plastic pad, a dashpot and a spring in parallel. The plastic pad is activated by stresses beyond a triggering stress resulting in permanent strain. The dashpot captures the increase of stress with an increase in strain rate [1] and the spring mimics hardening of the material causing an increase in stress at post yield strain [1] [4] [18] . The viscoplastic component has similarities with the one in Garcia’s model [12] but does not include a damage criterion. However a further development, including Garcia’s [12] damage criterion to the spring in the viscoplastic component, may be possible. The constitutive equations for the viscoplastic- component originate from Perzyna [34] [35] and are further described in Ottosen and Ristinmaa [36] .
![]()
Figure 1. Illustration of the rheological model for the proposed constitutive material model of vital cortical bone in longitudinal direction. The model consists of three different components (viscoelastic, viscoplastic and remodeling) to capture stress- strain relationship, relaxation, remodeling and creep behavior.
![]()
Table 1. Symbols used in the modeling and definitions.
![]()
Table 2. Overview of experimental studies referred to in the present study.
The yield function , according to Ottosen and Ristinmaa [36] , is defined as
, according to Ottosen and Ristinmaa [36] , is defined as
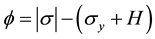 (3)
(3)
where the yield evolves when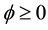 .
.
The plastic strain rate is defined as
 (4)
(4)
where
 (5)
(5)
An overstress function 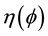 is defined according to the Norton creep power law [37] :
is defined according to the Norton creep power law [37] :
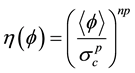 (6)
(6)
The stress 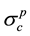 is an arbitrary reference stress. It is postulated that:
is an arbitrary reference stress. It is postulated that:![]() .
.
2.3. Remodeling component
The linear decrease in force in Perren’s et al. [8] in vivo experiment is interpreted as a reduction in stress due to remodeling of bone. In the present study the reduction of stress is modeled as a constant reduction of strain over time and the remodeling component is therefore expressed in terms of a constant strain rate:
![]() (7)
(7)
In the proposed model we define a remodeling parameter ![]() to:
to:
![]() (8)
(8)
2.4. Differential equation for the proposed bone model
By adding the different components into the rheological model, the differential equation for each spring-dash- pot-combination is derived.
Spring 1
![]() (9)
(9)
Spring 2- 4
![]() (10)
(10)
2.5. Calibration of model parameters
The magnitude of the viscoelastic, viscoplastic, relaxation, creep and remodeling parameters were obtained by fitting the model simulations to experimental results [1] [4] [8] [18] [27] by minimizing the error. The minimized error was found by using the constrained nonlinear optimization function (FMINSEARCHCON) available in MATLAB.
2.6. Viscoelastic and viscoplastic stress-strain behavior
The viscoelastic and viscoplasticstress-strain behavior of cortical bone is reported in Crowninshield and Pope [4] , McElhaney [1] and Melnis and Knets [18] . The simulations, by use of the proposed constitutive model with the calibrated parameter values, mimic the stress strain curves in these in vitro experimental studies.
2.7. Relaxation and remodeling behavior
The relaxation and remodeling behavior of cortical bone was identified using three in vivo data sets of reduction in force with time obtained from Perren et al. [8] . The proposed model presents relaxation as a reduction of stress with time. Therefore the axial force was converted to stress by assuming a cross sectional area of 160 mm2 for one sheep tibia. The other two sheep tibiae cross sectional areas were thereafter set to 186 and 290 mm2 respectively resulting in the same remodeling rate for the different sheep. The measurements in Perren et al. [8] started 3 h after the initiation of bone compression. Therefore the initial (at 0 s) strain level was adjusted to fit the measurements at 3 h in Perren et al. [8] .
2.8. Reversible and irreversible creep behavior
Creep behavior was identified using creep curves from the experiments of Melnis et al. [27] . Four different magnitudes of constant stress for the individual stress-strain tests were used (20%, 30%, 40% and 50% of ultimate stress![]() ). The ultimate stress (in Melnis and Knets [18]
). The ultimate stress (in Melnis and Knets [18] ![]() = 112 MPa, in McElhaney [1]
= 112 MPa, in McElhaney [1] ![]() = 144 MPa and Crowninshield and Pope [4]
= 144 MPa and Crowninshield and Pope [4] ![]() = 141 MPa) was determined by use of stress-strain curves at strain rates of 0.001 s−1 respectively. The constant stress was applied during 12,000 s and then released. For simulation purposes the stress was ramped up to a constant level during 1 s and ramped down during 1 s.
= 141 MPa) was determined by use of stress-strain curves at strain rates of 0.001 s−1 respectively. The constant stress was applied during 12,000 s and then released. For simulation purposes the stress was ramped up to a constant level during 1 s and ramped down during 1 s.
3. Results
Applying appropriate parameters values the predictions of the mechanical behavior of the bone agrees well with the results in experimental tests according to Figures 2-5.
![]()
Figure 2. Stress-strain curves predicted by the proposed model with corresponding experimental data for (a) Melnis and Knets [18] (b) McElhaney [1] and (c) Crowninshield and Pope [4] .
![]()
Figure 3. Prediction of creep behavior by the proposed model for the stress-strain tests of (a) Melnis and Knets [18] (b) Mc Elhaney [1] and (c) Crowninshield and Pope [4] with corres- ponding experimental data from Melnis et al. [27] .
The parameters for the viscoelastic component are presented in Table 3.
It seems that individual spring stiffness E1, E2, E3, E4, and E5, are 25% - 28%, 11% - 12%, 3% - 5%, 9% - 10% and 48% - 50%, respectively of total Young’s modulus (sum (E1 to E5)) regardless of stress strain test (Table 4).
The values obtained for the viscosity parameter u2 are in the same range when fitting the model to the experimental results of Melnis and Knets [18] , McElhaney [1] and Crowninshield and Pope [4] , representing relaxation times t2 of 3.3, 3.9 and 4.1 days respectively (Table 3). The viscosity parameter u3 represents fast relaxation with relaxation times t3 in the range of 1200 - 1330 s (Table 3). The viscosity parameters u4 and u5 represent even faster relaxation with relaxation times t4 and t5 in the range of 100 - 400 ms and 1 - 20 µs respectively
![]()
Figure 4. Prediction of reverse creep behavior by the proposed model for the stress-strain tests of (a) Melnis and Knets [18] (b) Mc Elhaney [1] and (c) Crowninshield and Pope [4] with corres- ponding experimental data from Melnis et al. [27] .
(Table 3). The values of the individual parameters obtained for the viscoplastic component, when fitting the model to the experimental results of Melnis and Knets [18] , McElhaney [1] and Crowninshield and Pope [4] , clearly differ (Table 5).
To capture the stress strain behavior for all strain rate experiments ![]() must be in the range of the yield point for the stress strain curve for the lowest strain rate. In the present model the value of
must be in the range of the yield point for the stress strain curve for the lowest strain rate. In the present model the value of ![]() shall be seen as a triggering value for the viscoplastic behavior for all strain rates. However to significantly evolve plastic strain
shall be seen as a triggering value for the viscoplastic behavior for all strain rates. However to significantly evolve plastic strain
![]()
Figure 5. Prediction of relaxation and remodeling behavior by the proposed model for the stress-strain tests of (a) Melnis and Knets [18] (b) McElhaney [1] and (c) Crowninshield and Pope [4] with corresponding experimental data from Perren et al. [8] .
(representing material yield) for increased strain rate increased stress is required. The stress-strain test (Figure 2(a)) of Melnis and Knets [18] resulted in a higher value of the hardening coefficient ![]() compared to the other stress-strain tests (Figure 2(b), Figure 2(c)) [1] [4] . In addition the magnitude of the yield stress value is higher for McElhaney’s [1] compressive test compared to those of the tensile tests [4] [18] . The parameter value obtained for the remodeling
compared to the other stress-strain tests (Figure 2(b), Figure 2(c)) [1] [4] . In addition the magnitude of the yield stress value is higher for McElhaney’s [1] compressive test compared to those of the tensile tests [4] [18] . The parameter value obtained for the remodeling ![]() component is presented in Table 6.
component is presented in Table 6.
![]()
Table 3. Parameters, for the individual stress-strain tests, of the viscoelastic component according to Figure 1 with time constants t. The parameters are calibrated by means of the least square method to fit stress-strain, relaxation, remodeling and creep experimental data..
![]()
Table 4. Contributions in % to the total Young’s modulus of the springs in the viscoelastic component, for the individual stress-strain tests, indicating the same distribution independent of test.
![]()
Table 5. Parameters for the stress-strain tests of the viscoplastic component according to Figure 1.
![]()
Table 6. Parameters for the stress-strain tests of the remodeling component according to Figure 1.
4. Discussion
Based on the results of the present study it can be concluded that the proposed model, with a suitable choice of model parameters reflecting the properties of the bone, is capable to predict the mechanical behavior of the bone. Simulations of the mechanical response, with the proposed model and calibrated model parameters, capture with good agreement the experimental stress-strain results obtained by Melnis and Knets [18] , McElhaney [1] , Crowninshield and Pope [4] , Perren et al. [8] and Melnis et al. [27] (Figures 3-5). Bone behaves differently in tension and compression [38] . Both tension and compression can be simulated by the present model. To capture compressive or tensile behavior the model parameters have to be determined by use of compressive or tensile test respectively. In addition the proposed model, with calibrated parameters, seems to be able to capture the creep and relaxation behavior. Bone is a complex material and the diversity of the measured bone material properties might reflect the quality, porosity, and testing condition of the bone specimen. In the proposed model the individual phenomena (viscoelasticity, plasticity, relaxation, creep and remodeling) are represented with three components reflecting the behavior of bone. The viscoelastic component contains four Maxwell elements (spring- dashpot combinations) that capture the strain rate dependency in the stress strain tests and the viscoelastic behavior found in relaxation and creep tests. The dashpots in Maxwell elements two and three have low viscosity and do not significantly influence the stress-strain curve. The increased Young’s modulus with increased strain rate is modeled, with Maxwell elements four and five. The sums of spring stiffness one to three for the individual tests [1] [4] [18] are similar to the Young’s modulus presented by Johnson et al. [11] . In the proposed model the plasticity component, with Norton creep, predicts the evolution of plastic strain at different yield stress levels for different strain rates observed in experiments (Figure 2). In the prediction of stress strain behavior the plastic pad in the proposed model has one triggering stress independent of strain rate. The triggering stress is lower than the physical yield stress observed in experiments in order to capture the stress-strain at low strain rates. This might reflect the observation that bone exhibits small irreversible strain, at quite low stress levels, due to sliding between the mineral and collagen as described by Mercer et al. [13] .
Iyo et al. [3] found that bone exhibits a slow relaxation in the order of 106 - 107 s and a fast relaxation in the order of 102 s. In the present model the slow relaxation is governed by the Maxwell element number two in the viscoelastic component (Figure 1) and the parameter values were derived from the in vivo experiment by Perren et al. [8] , resulting in a shorter relaxation time than that found by Iyo et al. [3] . The parameter values obtained from the data of Perren et al. [8] originate from in vivo tests and bone properties in live animals is probably different from those of Iyo et al. [3] investigating bone samples in vitro. Many factors, such as species, specimen type, storing and testing conditions, affect the material properties of bone [17] [18] [24] [39] . The initial drop in compression force within 14 days found by Perren et al. [8] can be explained by slow relaxation phenomena since the first registration of Perren´s et al. [8] was recorded 3 h after the initiated loading excluding the fast relaxation. The slow relaxation has been explained by Iyo et al. [26] to be related to the structural anisotropy of bone. In the studies by Halldin et al. [40] [41] , where an oversized implant was inserted in rabbit tibiae, a decrease in removal torque with longer implantation times was found. This decrease can be explained by the slow relaxation of bone. In the proposed model the parameter values in Maxwell element number three in the viscoelastic component (Figure 1) were obtained from the creep experiment of Melnis et al. [27] . The dashpot in Maxwell element three has a relaxation time of 1200 - 1300 s and differs one order of magnitude from those obtained by Iyo et al. [26] . The fast relaxation has been suggested by Iyo et al. [26] to be caused by relaxation of the collagen. Maxwell elements four and five have even shorter relaxation times of 1.4 - 3.3 ms and 1.4 - 21 µs respectively and model the Young’s modulus dependence of strain rate. The decrease in force after 14 days found by Perren et al. [8] and Blumlein et al. [31] was explained as a consequence of bone remodeling and seems to be linear over time. Therefore, in the suggested model, the remodeling component is expressed in terms of a constant strain rate reducing the stress over time. The proposed model, with calibrated parameter values, predicts with good agreement the slow relaxation and remodeling phenomena published by Perren et al. [8] (Figure 5). The total creep strain consists of two parts, one viscoelastic part that recovers when load is removed and one non-reversible viscoplastic part (Figure 1). The creep and reverse creep behavior of the proposed model, with calibrated parameters from the three different stress-strain tests [1] [4] [18] , are similar to those of the creep tests performed by Melnis et al. [27] (Figure 3, Figure 4). In a constant load situation the low viscosity of the dashpots four and five makes the viscous strain occur instantly. Thus they do not contribute to creep or reversed creep strains. The high viscosity of dashpot two, with a relaxation time in the range of 3.3 - 4.1 days, does not contribute significantly to the creep strain within the test time of 3.3 h (12,000 s) applied by Melnis et al. [27] . Thus the viscoelastic creep observed in Melnis et al. [27] is mainly captured by Maxwell element three as earlier discussed. The permanent deformation of bone has been suggested as a consequence of sliding between collagen and mineral that does not recover during unloading [13] . Non-recoverable creep strain in the viscoplastic component occurs when the yield condition is satisfied according to Equation (3). In the experiments of Melnis and Knets [27] non-recoverable creep strains occurred at stress levels below 40% of the ultimate stress, which is below the triggering stress of the plastic pad in the present study (Table 5). Therefore the present model is not able to capture the low non-recoverable creep strain behavior at low stress found by Melnis and Knets [27] . Melnis and Knets [27] indicated that a stress level around 50% of the ultimate stress may result in constant strain rate (secondary creep). In the simulations with the present model a constant strain rate was only obtained with parameter values derived from the stress-strain tests of Melnis and Knets [18] and a constant load corresponding to 50% of ultimate strength (Figure 3(a)). This secondary creep originates from an increase in strain of the viscoplastic component, which was not obtained for the other simulations. However with an increased stress level, simulations of the other tests [1] [4] (Figure 3(b), Figure 3(c)) would have exhibited similar creep behavior as Figure 3(a).
5. Conclusions
Analyzing the mechanical behavior of cortical bone during different longitudinal loading situations i.e. in vitro stress-strain relationship, in vivo relaxation, in vitro creep and in vivo remodeling has led to a proposed constitutive material model with associated rheological model that consists of four different components:.
1) A viscoelastic component modeling: a) the strain rate effect on Young’s modulus; b) the viscoelastic creep and c) the fast and slow relaxation. The viscoelastic component comprises 5 parts that can be tuned individually to achieve a desired model behavior.
2) A viscoplastic component triggering a) evolution of plastic strain and b) material hardening developed at different strain rates. In addition the viscoplastic component captures the secondary creep behavior.
3) A remodeling component modeling the decrease in prestress found in in vivo experiments. The decrease in prestress is interpreted as an effect of bone remodeling.
Depending on the simulation purpose the individual parts and/or components of the model may be included or excluded. The values of associated parameters should be determined by use of relevant experimental tests of bone.
Acknowledgements
This work was supported by the Swedish Research Council (621-2010-4760).
NOTES
*Corresponding author.