A Two-Stage Approach for Large-Scale Cascaded Hydropower System Operations ()
1. Introduction
Over the past twenty years, China has put much effort on hydropower development [1] . The total installed ca- pacity of hydropower has reached about 280 GW by the end of 2013, ranking first in the world. A number of large-scale cascaded hydropower systems with tens of plants have been put into operation or will be completed in future years, such as Hongshuihe River (10 plants), Wujiang River (11 plants), Lancangjiang River (14 plants), Jinshajiang River (13 plants), Daduhe River (16 plants), Yalongjiang River (21 plants). These large- scale cascaded hydropower systems are usually installed with the huge generating unit, whose capacity reaches 700 MW, 770 MW, even 800 MW. Correspondingly, the total capacity of single hydropower plant or cascaded hydropower system is also big. Different from conventional small cascaded hydropower plants, these large-scale hydropower systems play a more important role in the operation and management of electrical power systems and also need to face more complex operation requirements and limitations. The operational complexity and dif- ficulty are greatly increased with the increase in the number and total capacity of hydro plants in the power sys- tems. In fact, the basic and main requirement of the large-scale hydropower systems is to maximize their gener- ation and secure a stable supply of electric power to meet firm load demands while meeting the complex system physical and operational constraints. It is very urgent to find an effective and practical method for efficiently solving the optimization problem of large-scale hydropower system operations according to the features of China’s hydropower system.
Optimization of large-scale cascaded hydropower systems has been well known as a challenging practical and theoretical problem, which motivates strong demands for optimization techniques [2] . Many optimization me- thods are accordingly proposed and developed over the past several decades [3] -[5] . In general, these methods and models are classified into two types, mathematical programming techniques and heuristic programming methods. The former includes linear programming [6] [7] , quadratic programming [8] , nonlinear programming [7] , dynamic programming [9] , progressive optimal algorithms (POA) [10] -[12] , discrete differential dynamic programming (DDDP) [13] , dynamic programming successive approximation (DPSA) [14] , Lagrangian relaxa- tion [15] , network flow [16] , decomposition coordination method [17] , etc. The latter consists of artificial neural networks [18] , genetic algorithms [19] , simulated annealing algorithm [20] , ant colony algorithms [21] , particle swarm algorithm [22] , which were applied to optimal operation of hydropower systems after the 1990s.
Among the above optimization methods, POA is usually used to solve the long-term optimal operation of cascaded hydropower plants. The significant advantages of POA are that it not only avoids resolving the nonli- near objective functions and constraints in the solution procedure, but reduces dimensionality difficulties by decomposing a multi-state decision problem into a series of non-linear programming two-stage problems. However, POA easily converges to a local optimum for complex problems with complex nonlinear relationship and spatial coupling constraints. To enhance the quality of the optimization solutions, it may be a feasible way to develop a hybrid method by incorporating POA with other global search algorithms.
The paper presents a two-stage approach to cope with the long-term optimal operation of cascaded hydropower systems. This approach combines POA with QP to improve the optimization results. POA is used at the first stage to generate a local optimal result, which will be selected as the initial feasible solution of QP method employed at the second stage. Around the initial solution, a rational local search range for QP method is then determined, where the nonlinear water level function and tailrace level function can be linearized nearly with high accuracy. The simplified optimization problem is formulated as a QP model with a quadratic generation function and a linear set of constraints, and solved using the available mathematic optimization software package. Simulation is performed on the long term operation of Hongshuihe River hydropower system which is located in southwest China and consists of 9 built hydropower plants. Results obtained from the proposed approach show a significant increase in the total energy production compared to the results from POA.
2. Problem Formulation
2.1. Objective
This paper uses the objective of maximizing total energy production which is a classic objective for hydropower systems [23] . The total energy produced during the studied horizon is defined as the objective value. Here it can be formulated as following:
 (1)
(1)
where m = the reservoir index; M = the total number of reservoirs; t = the period index; T = the previous time index under consideration; pm,t = average generation of plant m in period t, in MW; Δt = time step in period t, in seconds.
2.2. Constraints
Equation (1) is subjected to the following constraints:
1) Water balance:
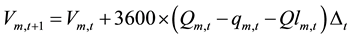 (2)
(2)
This equation ensures the inflow and outflow balance between interconnected plants. Where Vm,t = storage in reservoir m in period t, in m3; Qm,t = inflow into reservoir m in period t, in m3/s; qm,t = turbine discharge of plant
m in period t, in m3/s; Qlm,t = spill flow of reservoir m in period t, in m3/s. ; K is the total
; K is the total
number of immediate upstream plants of the mth plant; Qnm,t = local inflow into reservoir m in period t, in m3/s;  = flow from the upstream reservoir k into reservoir m in period t, in m3/s;
= flow from the upstream reservoir k into reservoir m in period t, in m3/s;
2) Specified target demand for single reservoir:
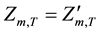 (3)
(3)
where 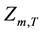 and
and 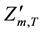 are final forebay elevation and specified forebay elevation target of reservoir m at the ending of period T, in m.
are final forebay elevation and specified forebay elevation target of reservoir m at the ending of period T, in m.
3) Turbine discharge capacity for single plant:
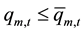 (4)
(4)
where  maximum turbine discharge of plant m in period t, in m3/s.
maximum turbine discharge of plant m in period t, in m3/s.
4) Discharge capacity for single reservoir:
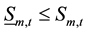 (5)
(5)
where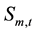 ,
, 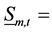 total discharge and minimum discharge from reservoir m in period t, in m3/s.
total discharge and minimum discharge from reservoir m in period t, in m3/s.
5) Minimum and maximum forebay elevation:
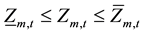 (6)
(6)
where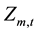 ,
,  ,
, 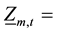 forebay level of reservoir m, its maximum and minimum forebay level, in period t, in m.
forebay level of reservoir m, its maximum and minimum forebay level, in period t, in m.
6) Generation capacity for single plant:
![]() (7)
(7)
where![]() ,
, ![]() maximum and minimum average generation from plant m in period t, in MW.
maximum and minimum average generation from plant m in period t, in MW.
7) System generation capacity for cascaded hydropower system:
![]() (8)
(8)
where![]() ,
, ![]() maximum and minimum generation of hydropower system in period t, in MW.
maximum and minimum generation of hydropower system in period t, in MW.
3. Model Solution
The paper solves the above optimization problem using the developed two-stage approach which combines the progressive optimality algorithm (POA) with quadratic programming (QP). In this approach, the first stage determines the initial feasible solution using POA, and the second stage improves the obtained solution by using QP method. The following two sections describe the solution process at each stage, respectively.
3.1. Determine the Initial Solution Using POA
POA has been shown to have great advantages as an effective method for solving large-scale hydropower system operations. This method has some merits, such as no need for discretizing the state variables, no resolving or linearization of nonlinear objective functions and constrains, etc. Basically, POA solves this kind of long- term hydropower system operations by repeatedly resolving a two-stage subproblem from time-step 1 to T. For each subproblem, the goal is to determine optimal state variables ![]() by fixing values of
by fixing values of![]() ,
,![]() . Our previous work has given an elaboration about the detailed solution procedure of POA for solving the hydropower system operations. The readers can refer to [12] .
. Our previous work has given an elaboration about the detailed solution procedure of POA for solving the hydropower system operations. The readers can refer to [12] .
3.2. Improve the Solution Using QP
Around the initial solution obtained at the first stage, a rational local search range for QP method is determined, where the nonlinear water level function and tailrace level function can be linearized nearly without losing accuracy. The simplified optimization problem is then formulated as a QP model with a quadratic generation function and a linear set of constraints, and solved using the general mathematic optimization software package.
First of all, the decision variables should be chosen to formulate the problem as a QP one. In this study, the forebay level, turbine discharge, and spill at all periods are used as the decision variables, i.e.![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Obviously, Equations (3)-(6) are the linear equa- lity and inequality constraints. Equations (2), (7), (8) are nonlinear constraints, and need to be linearized. Moreover, Equation (1) needs to be converted to a quadratic objective function of decision variables.
. Obviously, Equations (3)-(6) are the linear equa- lity and inequality constraints. Equations (2), (7), (8) are nonlinear constraints, and need to be linearized. Moreover, Equation (1) needs to be converted to a quadratic objective function of decision variables.
For each reservoir m, the storage at period t can be expressed as the linear function of the forebay level.
![]() (9)
(9)
where k = the section index within the bounds of level.![]() ,
, ![]() are constants.
are constants.
For each plant m, the tailrace elevation ![]() at period t can be described as a linear function of turbine dis- charge, as well as spill. We can express the tailrace elevation by the following relationship:
at period t can be described as a linear function of turbine dis- charge, as well as spill. We can express the tailrace elevation by the following relationship:
![]() (10)
(10)
where![]() ,
, ![]() are also constants.
are also constants.
For each plant m, the head losses in the penstock at period t are expressed as a linear function of turbine dis- charge, shown in Equation (11). Thus the net head is obtained by subtracting head losses from the gross head, shown in Equation (12).
![]() (11)
(11)
![]() (12)
(12)
where![]() ,
, ![]() are also constants.
are also constants.
Based on the above linear relationships of decision variables, the original objective function can be reformulated as a quadratic function of decision variables.
![]() (13)
(13)
Inserting Equation (9) into Equation (2) gives
![]() (14)
(14)
where k1, k2 are the section indexs within the bounds of level.
For each plant m, water rate ![]() at period t can be expressed as a linear function of net head
at period t can be expressed as a linear function of net head![]() , seen in Equation (15).
, seen in Equation (15).
![]() (15)
(15)
where![]() ,
, ![]() are also constants.
are also constants.
By inserting ![]() into Equation (15), the upper bound of power generation can be reformulated as
into Equation (15), the upper bound of power generation can be reformulated as
![]() (16)
(16)
In a similar way, the lower bound of power generation can be reformulated as
![]() (17)
(17)
For the system constraint (8), we use the new multipliers to convert the generation limitation into equivalent discharge limitation. The new system constraints are
![]() (18)
(18)
where![]() ,
, ![]() are conversion multipliers, which are updated during the calculation process.
are conversion multipliers, which are updated during the calculation process.
Consequently, the original optimization problem is described as a QP model with a quadratic objective function (13) and linear constraints (3)-(6), (14), (16)-(18). The QP model can be easily solved using the existing standard algorithm provided in some mathematic optimization software such as MATLAB and LINGO.
4. Case Study
The developed approach is implemented to the cascaded hydropower plants in the main stream of Hongshuihe River operated by SCPG and Guangxi Power Grid (GXPG). Hongshuihe River is located in southwest China, and flows from northwest to southeast with about 1050 km stretch, a drainage area of 190,000 km2 as well as annual mean precipitation of 1200 mm. The River originates from Nanpanjiang River in Yunnan Province, later known as Hongshuihe by the confluence with Beipanjiang River in Guizhou Province. There are also two main tributaries in the down reach of Hongshuihe River, Yujiang River and Liujiang River. Correspondingly, 10 cas- caded hydropower plants are under planning stage in the main stream, 9 of which have been put into operation from upstream First Reservoir of Tianshengqiao (FROTSQ) to downstream Qiaogong plant, with an installed capacity of 10,739 MW. Figure 1 shows the hydropower systems consisting of 10 plants included in the main stream. In this case study, five main hydropower plants from upstream FROTSQ to downstream Yantan are in- cluded. Among these plants, FROTSQ, Longtan, and Yantan have large storage capacity, and Second Plant of Tianshengqiao and Pingban have little storage capacity.
To test the proposed approach, two different schemes with different flow are given. The first flow scheme uses 25% frequency to determine the local inflow, and the second scheme uses 50%. Table 1 compares the op- timization results and computation times between our approach and POA for each flow scheme. Meanwhile, to demonstrate the feasibility of the optimization results, Figure 2 illustrates the entire generation schedules and forebay elevation trajectory obtained from our approach for the second scheme.
![]()
Figure 1. Distribution map of Hongshuihe river.
![]() (a)
(a)![]() (b)
(b)![]() (c)
(c)
Figure 2. The optimization generations and levels obtained from our approach for the second flow scheme. (a) FROTSQ; (b) Longtan plant; (c) Yantan plant.
![]()
Table 1. Optimization results obtained from two approaches.
As can be seen from Figure 2, three reservoirs work at available levels during the operational horizon. The forebay elevation in FROTSQ decreased closely to the dead level before flood season so that more storage ca- pacity is left for the later floods. Moreover, by making full use of the large storage capacity of Longtan reservoir, Yantan always operates at the maximum level during the whole time horizon and enhance the generation effi- ciency.
It is easily seen from Table 1, that our approach provides better results than POA. An average increase of to- tal energy of 542 million kWh during one year is provided by our approach, showing efficient search ability of this approach. We can give a rational explanation about the optimization results from two aspects. One is that using the optimized solution from POA as the initial solution improves the search efficiency of this approach to some extent. The other is that the problem is further optimized by solving a sequence of QP subproblems based on different conversion multipliers. QP method avoids two-stage search procedure of POA and thus improves the quality of optimal solutions. Although our approach costs more computation time than POA, 31 s or 28 s is also very short for real-world engineering.
5. Conclusion
With the rapid development of China’s hydropower, there has been a pressing need for efficient and feasible optimization methods to enhance the production benefit of large-scale hydropower systems. This study proposes a two-stage approach and implements it to the Hongshuihe hydropower system. The simulation results from a case study demonstrate that the proposed approach can enhance the energy production of cascaded hydropower plants. It is also concluded that integrating multiple typical optimization algorithms maybe a feasible way to ef- ficiently solve the complex optimization problem of large-scale hydropower system operations.
Acknowledgements
This research was supported by National Natural Science Foundation of China (No. 51209031) and the Funda- mental Research Funds for the Central Universities (No. DUT14RC(3)089), and “Xinghai Scholar” talents training plan of Dalian University of Technology.