Nitrogen Distribution Model: A Farmer and Farm-Centred Model to Monitor N Movement in the Soil ()
1. Introduction
Nitrogen (N) is the most important determinant of plant growth and crop yield. Plants lacking N show stunted growth and yellowish leaves. Plant growth and crop yield usually increase when N is added [1] . However, too much N can also cause problems which may extend to plants, humans, animals, and the environment. For exam- ple, in plants, too much N will lead to weak stems in grain crops (lodging), reduce quality in fruit such as peaches and apples, lower sugar content in sugar beets, and may lead to an accumulation of nitrate in the edible foliage of plants such as spinach and forage crops [2] . N can contaminate groundwater to a point at which it may become a health hazard (10 ppm). Matching N availability in soil solution and crop uptake needs is critical to improving maize production. [3] reported that best nitrogen and water management practices can reduce the probability of nitrate leaching into groundwater and maintain profitable yields. The big question in the manage- ment of nitrogen has been how much nitrogen is enough in crop production for give desirable crop yields with low cost while avoiding excess N-induced problems. Owing to the complexity of soil and crop systems, it is dif- ficult to account for the observed N responses, and to ascertain that specified output is the result of a specified N input [4] . The behavior of N in the soil system is complex, yet an understanding of basic processes is essential for a more efficient N management program [5] . The basic processes of Nitrogen in soil are leaching, denitri- fication, volatilization, crop removal, and soil erosion and runoff. Leaching is the loss of soluble 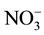 as it moves with soil water below the root zone. Nitrate can be leached from any soil applied water exceeds the water holding capacity of the soil leaving additional water to freely move down through the soil profile with soluble nitrogen. Understanding of movement of water with solute in soil can help to reduce nitrogen losses through leaching and maximize economic returns of smallholder farmers. The movement of N in the soil is influenced by leaching and crop removal. Leaching which is due to movement of nitrogen is governed by advection and dispersion equations while crop removal is governed by rate of plant uptake. The majority of nitrate ions
as it moves with soil water below the root zone. Nitrate can be leached from any soil applied water exceeds the water holding capacity of the soil leaving additional water to freely move down through the soil profile with soluble nitrogen. Understanding of movement of water with solute in soil can help to reduce nitrogen losses through leaching and maximize economic returns of smallholder farmers. The movement of N in the soil is influenced by leaching and crop removal. Leaching which is due to movement of nitrogen is governed by advection and dispersion equations while crop removal is governed by rate of plant uptake. The majority of nitrate ions  do not bind to the soil solids because they carry negative charges and are greatly influenced by advec- tion (defined as the flux of solute due to the movement of water containing the solute). The movement of any solute including nitrogen in the soil where maize is growing is given as follows [6] :
do not bind to the soil solids because they carry negative charges and are greatly influenced by advec- tion (defined as the flux of solute due to the movement of water containing the solute). The movement of any solute including nitrogen in the soil where maize is growing is given as follows [6] :
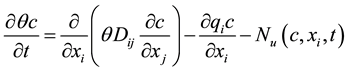 (1)
(1)
This mathematical expression has all three factors that influence the movement of nitrogen in the soil and these are advection, dispersion and plant nitrogen uptake.
This paper presents the work and steps used to develop NDM. NDM has been developed to ensure that it re- sponds to increasing need of managing nitrogen in agricultural systems characterized by smallholder farmers who do not have adequate resources to collect intensive data for modeling. NDM has parameters that are explicit and mostly intuitive and maintains good balance of simplicity and robustness.
2. Methodology
2.1. Advection-Dispersion Equation
The modes of nitrogen transport in soil are predominantly governed by advection and dispersion [6] -[8] . The mathematical expression of Advection-Dispersion Equation is given as follows:
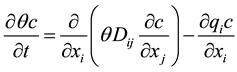 (2)
(2)
where, t is time, c is the N concentration in the liquid phase, xi and 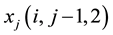 are spatial coordinates, Dij are components of dispersion coefficient tensor, qi is the ith component of the volumetric flux density. The volume- tric flux density
are spatial coordinates, Dij are components of dispersion coefficient tensor, qi is the ith component of the volumetric flux density. The volume- tric flux density 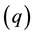 to be employed in the above equation determines the nature of transport of dissolved N with flowing water. Thus, use of the flow equation is required to calculate the volumetric flux density.
to be employed in the above equation determines the nature of transport of dissolved N with flowing water. Thus, use of the flow equation is required to calculate the volumetric flux density.
2.1.1. Advection Equation
Advection is defined as the flux of solute due to flow of water containing the solute. It is a product of water flux and the solute concentration  and can simply be expressed as [9] :
and can simply be expressed as [9] :
 (3)
(3)
1) Determination of N concentration of solute in the soil
The following equation was used to calculate concentration of nitrogen in the soil.
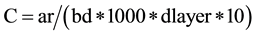 (4)
(4)
where:
・ C is concentration of solute (kg/L3 of soil);
・ ar is N application per hectare (kg/ha);
・ bd is bulk density (g/m3);
・ dlayer is depth of layer (mm).
Solute is substance dissolved in a liquid. Concentration is measured in [mass/length3] (mg/L). Concentration is function of time, directions,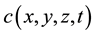 .
.
2) Determination of water flux 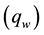
Triscan Sensor was used to collect soil water content in (d) depth of water in each layer (L of water/L of soil). This water depth was multiplied by row spacing (r) and planting spacing (s) to have (q) volume of water availa- ble within each layer of maize root zone as presented in below equation:
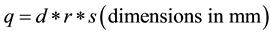 (5)
(5)
The water flux qw was determined by considering volume of water (q) crossing the cross-section area of maize rootzone (mm3), lateral conductivity (Kh in mm/day), and ground surface slope (m/m) as presented in equation below:
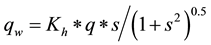 (6)
(6)
where:
Kh = horizontal conductivity (mm/day);
q = soil volumetric water content;
s = surface slope (m/m).
2.1.2. Dispersion Equation
Dispersion is the spreading out of solute due to variations in water velocity within individual pores, across pores with differing sizes and shapes, and across interconnected pore pathways with different geometries. It allows solute to come to an equilibrium concentration within the soil solution and between regions where the soil solu- tion is mobile or immobile [10] :
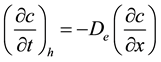 (7)
(7)
where  is the solute flux due to dispersion;
is the solute flux due to dispersion;
 is the dispersion coefficient, estimated as follows [11] [12] :
is the dispersion coefficient, estimated as follows [11] [12] :
![]() (8)
(8)
where:
・ D is the diffusion coefficient in water filling the pores (for N in water is 1.88 × 10−5 m2∙s−1);
・ τ is the tortuosity of soil (dimensionless), values are between 0.21 to 0.35 for unsaturated sandy loam soils, and between 0.59 to 0.84 for saturated sandy loam soil by [13] ;
・ θ is soil volumetric moisture content.
2.2. Plant Nitrogen Uptake
Another influence that will determine nitrogen movement in the soil is plant uptake. The uptake of water and nutrients by plant roots will create a gradient in regions surrounding the roots. With the general principle of hy- draulic gradient influencing water movement, then water and nitrogen will move towards plant roots where there is a negative gradient. Plant nitrogen uptake, Nu, is the function of time and coordinates. It is related to water uptake in that the nutrient gets taken up by the plants with the water. The Nu is governed by the following equa- tion:
![]() (9)
(9)
![]() (10)
(10)
where ![]() is a prescribed dimensionless function of the soil pressure head ranging between 0 and 1. Soil pressure is a function of soil moisture content in the soil. At saturation point, soil pressure is 0 and soil pressure head is 1. At wilting point soil pressure is at maximum and is 1 while soil pressure head is 0; i.e. At SAT,
is a prescribed dimensionless function of the soil pressure head ranging between 0 and 1. Soil pressure is a function of soil moisture content in the soil. At saturation point, soil pressure is 0 and soil pressure head is 1. At wilting point soil pressure is at maximum and is 1 while soil pressure head is 0; i.e. At SAT, ![]() , at LL15,
, at LL15, ![]() (Boundary).
(Boundary).
Smax is the potential water uptake rate which equal to crop evapotransipiration (Smax = ETc).
3. Development of NDM
The left graph of Figure 1 shows that concentration of solute in soil decreases with time. For example, before application of nitrogen fertilizer, the concentration of nitrogen was low but when nitrogen fertilizer was applied, the concentration of nitrogen increased. Due to leaching and uptake by maize, nitrogen concentration decreased. The right graph of Figure 1 shows that at point where nitrogen fertilizer has been applied, the concentration of nitrogen is high compared to the surroundings.
The following assumptions have been drawn from Figure 1 and have been used in development of the model.
1) At the time of fertilizer application, the soil where fertilizer is applied has highest concentration of nitrogen than the surroundings;
2) Movement of nitrogen is from the point of application to the surrounding;
3) Concentration is mass of nitrogen/volume of soil (to be calculated by bulk density);
4) All NH4-N in fertilizer is converted to NO3-N immediately upon fertilizer application, and is completely dissolved in applied water;
5) There is no capillary rise, and water table lies far below the surface.
3.1. Input and Output Variables of the Model
NDM has been developed by including all three factors that influence solute transport in the soil and these are advection, dispersion and plant uptake. It would have been difficult to use the model if the input parameters were soil moisture content, rate of nitrogen uptake by maize plant, concentration of nitrogen in the soil because cost associated with equipment need to capture such type of data. In order to simplify the model, the input pa- rameters have been simplified to volume of water applied in m3 and the model is then generating the depth of water in mm. The depth of applied water in the soil is linked to calculation of soil moisture content. The input parameter of the model is quantity of fertilizer applied in kg/ha and the model is generating quantity of nitrogen applied presented in N kg/ha. This input parameter is linked to the nitrogen concentration in the soil, which is an integral component of both advection and dispersion equations present in Equation (1). The other input parame- ter that has been used in the model is maize growth stage. The maize growth stage such as emergence, develop- ment, mid- and late-stages is generating crop coefficient (Kc) which is being used to calculate actual crop evapo- transpiration (ETc). The ETc has been assumed as potential water uptake rate (Smax) in the uptake component of the equation.
The model has included two other input parameters of farmer and farm. The input parameters under farmer consists of name of a farmer, district, Traditional Authority (TA), village and his/her mobile number. The farm
![]()
Figure 1. It shows behaviors of concentration with respect to time and distance.
input parameters consists of land under cultivation, general slope of the farm, general soil type, irrigation me- thod, and district where the farm is ( here the model has assumed that some farmers might have two or more farms in different districts). These input parameters have been included to ensure that the model is farmer-center- ed that will enable them to have specific recommendations as per their specific agricultural production require- ments. Figure 2 shows a schematic diagram of NDM with input and output information.
3.2. The Input Data Files of the Model
The NDM has five input data files namely Farmer Date file, Farm Data file, Water Data file, Fertilizer Data file, and Crop Data file. Within each data file, there are more than three input parameters that need to be entered in the model. These input parameters have been designed in such way that they are not difficult for users to collect and input them in the model. If the data input requires sophisticated equipment to collect them in the field, it may limit the wider application of the model [14] .
The NDM is written in programming language of C++. The model used this programming language because NDM was developed so that it can be incorporated in the Soil Water Module of APSIM model as subroutine. The programming language of APSIM is C++; hence to ensure compatibility, the NDM had to be developed in the same programming language. Figure 3 shows the flow chart of the model.
3.3. The Nitrogen Distribution Model Interface
Figure 4 presents the interface of the NDM. The interface has four main input data sets namely Farmers and Farms under general information category, and Water and Fertilizer under inputs category. The last category of processes has Simulation and Set up.
When clicked on Farmer file, the four operations will appear and these are New farmer, Update Farmer De- tails, Delete Farmer or Add Farm. The user will select the operation that he/she want to operate. Another advan- tage of this model is that it also acts as database to keep information of farmers and their farms; hence it is easy to track and give advice to farmers.
![]()
Figure 2. Schematic diagram of NDM with input and output information.
After data is entered under farmer file, the next step is to enter details of the farm. The model has assumed that one farmer might have different farms with different characteristics. In fact, the agricultural production sys- tem of most of the smallholder farmers is that they have several patches of land which they for crop production. This model has taken this agricultural production system into consideration. The model would provide informa- tion to farm specific.
4. Conclusion
The conceptual framework, design, structure and key algorithms of the NDM have been described to highlight the distinctive features and peculiarities of the model. The model requires low number of parameters and input data to simulate movement and distribution of nitrogen in the soil under irrigation. Unlike other previous similar models, the strength of this model is that input parameters are very minimum and easy to capture and enter in the interface. To capture the input parameters of water and nitrogen does not sophiscated equipment and hence smallholder farmers. The parameters of the model are explicit and maintain good balance of accuracy, simplicity and to some extent robustness. The model is aimed at ensuring that informed decisions are made on proper management of water and nitrogen resources on a farm. Another important application of the model is that it can be used as database for smallholder farmers so that they easily be tracked be advised on good agricultural practices. The model is still under development but will be tested under different soil types and crops so that it can be widely used by users.
NOTES
*Corresponding author.