Flywheel Energy Storage with Mechanical Input-Output for Regenerative Braking ()
1. Introduction
Flywheel energy storage is an appealing and much studied concept that has failed to compete with battery storage in hybrid vehicles. One obstacle is the complexity involved in adequately controlling the energy flow from flywheel to propulsion system and vice-versa. An approach is to interpose a generator-motor between the two, resulting in the conversion of energy from kinetic to electrical and back to kinetic. The design requirements of such a system in a hybrid vehicle are examined in [1] . This idea is also incorporated in [2] . A theoretical and experimental evaluation of an advanced concept in which the motor-generator rotor is also the flywheel energy storage element capable of operating at speeds up to 60,000 rpm is presented in [3] . A conceptually simple means of transferring the kinetic energy due to a vehicle’s motion to a flywheel and then transferring it back to accelerate the vehicle, is based on a continuously variable transmission (CVT) whose speed ratio is varied to impose a deceleration of the power input shaft and an acceleration of the power output shaft. To bring the system into operation, clutches are used. However, the range of speed ratios of a CVT is rather limited and may not permit matching the ratio required when engaging the clutches causing slip and power loss. To solve this problem, gear shifts may be introduced [4] . An elaborate scheme is to introduce means to accelerate or decelerate the flywheel prior to engaging the clutches to bring the speed ratio required of the CVT to within its capability [5] resulting in the addition of a secondary energy storage, such as batteries, and the need for conversion of energy from one form to another. In principle, energy may be extracted from or added to a flywheel by varying its moment of inertia, as in the concept described in [6] ; however the practicality of this method with respect to weight and space requirements seems questionable. A mechanical arrangement intended for the storage of a modest amount of energy as is the case in regenerative braking, is proposed in this paper. Because the transfer of kinetic energy both ways between the vehicle and the flywheel takes place directly without conversion to another form of energy, high efficiency is anticipated. The system proposed is based on a transmission that is continuously variable but does not fit the usual concept of a CVT. Although it lacks flexibility with respect to torque control, it has the virtue of simplicity.
2. Concept Description
The means for transferring the kinetic energy of the vehicle’s motion to the flywheel in the proposed arrangement is a cable that winds onto a pulley geared to the vehicle’s propulsion driveshaft as it unwinds from another pulley geared to the flywheel and then operates in reverse for the transfer of energy in the opposite direction. Figure 1 is a schematic diagram of the system. The cable windings are in one plane resulting in an effective pulley radius that increases when the cable is winding onto it and decreases when unwinding from it. Thus, an increasing driven-to-driving pulley velocity ratio is obtained during a period of energy transfer in either direction, corresponding to vehicle braking or acceleration. These periods are limited by the length of the cable, which must stop unwinding from a pulley before the point of attachment to it is exposed. Speed reduction means, not shown in Figure 1, would obviously be required between the flywheel and gear Gf.
Referring to Figure 1, two identical mechanisms, one on the vehicle’s propulsion side and one on the flywheel side, are used to control the system. The subscripts “p” and “f” will be used to denote their respective components. In each of these mechanisms, the double bevel gear A, B may slide on the pulley’s splined shaft allowing either A or B to mesh with gear G or, as depicted in Figure 1, to remain in a neutral mid position. Also, overruning clutches, R, are provided between each pulley and gear B. They allow power to flow from gear B to the pulley only when their shaft is decelerating and only in the opposite direction when accelerating. Additionally, a small servo motor, M, whose function will be explained below, is coupled to each pulley.
To activate the system for braking, with clutches Cp, Cf, disengaged, the double gears A, B are displaced in the downward direction until each gear B meshes with the corresponding gear G. Engaging then both clutches simultaneously causes the pulley Pp to start rotating in a direction to wind up the cable on it and drive pulley Pf in
![]()
Figure 1. Schematic diagram of flywheel energy storage system.
a direction to accelerate the flywheel. Operation of the system for acceleration is similar, except that the double gears A, B must first be displaced in the upward direction until each gear A meshes with the corresponding gear G.
Each servo motor, M, can apply a small torque in the direction to tighten the cable. A control system monitoring the pulleys’ speed and angular position, activates one of these motors if the pulleys’ speed ratio deviates from the ratio dictated by their instantaneous angular positions, and thus, instantaneous radii. The motor which is activated is the one corresponding to the pulley that is lagging behind and provoking therefore a slack in the cable. This action corrects the error. Because of the overrunning clutch, the servo motor only transmits torque to the pulley. The control system operates continuously even when the clutches Cp, Cf, are disengaged. Thus, when energy transfer in either the braking or accelerating mode is initiated, the pulleys angular positions are consistent with their speed ratio, avoiding clutch sliding or cable shock loading.
The control system also blocks the transfer of energy for braking if the pulley radius on the flywheel side is less than a specified lower limit, and also blocks the transfer of energy for accelerating if that radius exceeds an upper limit.
As mentioned earlier, the proposed concept lacks flexibility in that the torque for braking or accelerating follows a variation dependent on fixed design parameters. This same situation is encountered in the hydropneumatic system for brake energy recovery which uses a fixed displacement pump-motor [7] . As in that case, a dissipative brake can complement the regenerative brake. The latter is used only when the torque required is equal or greater than what it can provide, the excess needed being supplied by the dissipative brake. Below that torque, braking is entirely dissipative. When using the stored energy to accelerate the vehicle, a similar approach would be used; that is, the vehicle’s power plant is used exclusively for light acceleration, or to provide torque in addition to that provided by the flywheel system. A guiding consideration in the design of the flywheel recovery system is the maximization of the energy recovered on the basis of a suitable drive cycle.
3. Dynamic Analysis
In order to obtain relations between the effective radii of the pulleys, rf, rp, and between their angular displacements, consider an infinitesimal counterclockwise rotation dθf of pulley Pf causing a rotation dθp of pulley Pp. Then,
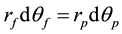 (1)
(1)
Setting θf = θp = 0 when rf has the minimum value r1, and rp has the maximum value, r2,
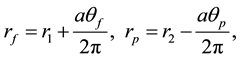 (2)
(2)
where a represents the cable diameter.
From the above equations, it is found that the total rotation of either pulley between its extreme r values is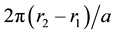 .
.
An expression for the required length of cable will now be obtained. Consider a differential rotation θf of the flywheel pulley causing an increased ds in the length of cable wound on said pulley. Then, from the first of Equation (2):
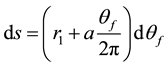
Integrating the above equation between the limits 0 and 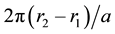 yields, after simplification:
yields, after simplification:
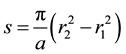 (3)
(3)
Substituting the expressions for rf, rp given by Equation (2) in Equation (1) yields the following equation:
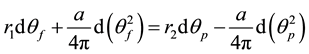
Integrating, applying the condition that θp = 0 when θf = 0, and rearranging, yields the following equation:
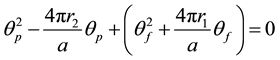
The solution of the above quadratic equation for θp consistent with the initial conditions is:
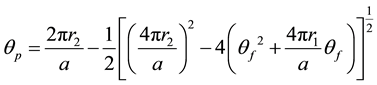 (4)
(4)
Differentiating Equation (4) and setting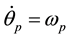 ,
,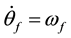 :
:
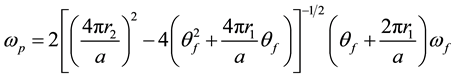 (5)
(5)
For convenience, define
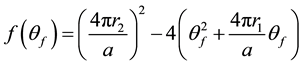 (6)
(6)
Then θp may be written as:
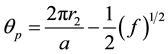 (7)
(7)
and, from the second of Equation (2) and Equation (7),
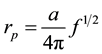 (8)
(8)
Also,
![]() (9)
(9)
and
![]() (10)
(10)
Let F be the cable tension, Ip the reflected moment of inertia of the vehicle on the shaft of pulley Pp, and If that of the flywheel on the shaft of pulley Pf. Then
![]() (11)
(11)
Dividing the first of Equation (11) by the second one, and rearranging:
![]() (12)
(12)
But![]() , and
, and![]() , which substituted in Equation (12) results, after some manipulation, in
, which substituted in Equation (12) results, after some manipulation, in
![]() (13)
(13)
The RHS of Equation (13) is considered to be a function of θf and ωf in view of Equation (2), Equation (4), Equations (7)-(10). Thus, Equation (13) together with
![]() (14)
(14)
constitute a set of differential equations for θf and ωf.
4. Illustrative Example
The previously developed analysis will now be applied assuming Ip = If and the following values of a, r1, and r2, made dimensionless by dividing by “a”:
![]()
Then, from Equation (2), the total rotation of either pulley when r goes from r1 to r2 or vice-versa is 40π = 125.66 rad. Also, from Equation (3), the required length of cable is 2513a.
The differential Equation (13), Equation (14) were solved numerically with the following initial conditions:
![]()
From Equation (2), the first of the above conditions implies rf = r1 initially. Thus, the solution represents a deceleration of the flywheel and acceleration of the vehicle.
Figure 2 shows how θf and θp vary during the process lasting 8.75 seconds and ending when rf reaches the value r2. Figure 3 shows the corresponding variations of rf and rp and Figure 4 those of ωf and ωp. The speed reduction ratio, ![]() , is plotted as function of time in Figure 5. As seen, it starts as 3.0 and has a final value of 0.333. The acceleration, αp , of the propulsion driveshaft is shown in Figure 6.
, is plotted as function of time in Figure 5. As seen, it starts as 3.0 and has a final value of 0.333. The acceleration, αp , of the propulsion driveshaft is shown in Figure 6.
![]()
Figure 3. Variation of pulleys’ radii in non-dimensional units.
![]()
Figure 4. Variation of pulleys’ angular velocities.
![]()
Figure 5. Variation of speed reduction ratio,![]() .
.
An estimate of the energy losses for this process will now be made assuming a = 6.4 mm (1/4” dia. cable) a vehicle with a mass, m, of 1300 kg, 0.6 m diameter tires, and a velocity ratio![]() , where ωw is the tire angular velocity. With these values, the vehicle’s kinetic energy would increase from 10.8 kJ to 93.6 kJ during the process considered. Also, Ip, the reflected vehicle inertia on the shaft of pulley Pp, is
, where ωw is the tire angular velocity. With these values, the vehicle’s kinetic energy would increase from 10.8 kJ to 93.6 kJ during the process considered. Also, Ip, the reflected vehicle inertia on the shaft of pulley Pp, is![]() . Thus, the torque
. Thus, the torque![]() . This torque, as well as the cable tension, F, may be found at any time using the values of αp given by the graph of Figure 6. In particular, the initial and final values are found to be respectively: for Tp, 1034 N×m and 337 N×m, and for F, 5386 N, and 5074 N. Also, the average values of these, obtained from the increase in the vehicles kinetic energy, the pulley’s total angular rotation and the length of cable transferred, are 658.9 N×m and 5148 N respectively.
. This torque, as well as the cable tension, F, may be found at any time using the values of αp given by the graph of Figure 6. In particular, the initial and final values are found to be respectively: for Tp, 1034 N×m and 337 N×m, and for F, 5386 N, and 5074 N. Also, the average values of these, obtained from the increase in the vehicles kinetic energy, the pulley’s total angular rotation and the length of cable transferred, are 658.9 N×m and 5148 N respectively.
The main energy losses are considered to occur at the gear meshes. Two of these correspond to bevel gears, which will be assumed to be of the spiral type. Also, two gear speed reducers would be required, one on the flywheel side of the mechanism and one on the propulsion side. These are assumed to use helical gears. From [8] , the efficiencies of spiral bevel gears range from 95% to 99%, and those of helical gears, from 94% to 98%. Average values of 97% and 96% respectively will be assumed. Much smaller losses are associated with the bearings which would, most appropriately, be cylindrical open roller bearings with a cage. From [9] , the coefficient of friction expected would be 0.0011, that is, the resisting torque would be this value times the radial load times the shaft radius. Thus, if a reasonable value of the pulleys’ shafts diameter of 24 mm is assumed and the average transmitted torque of 658.9 N×m considered, the bearing resisting torques of both pulleys add up to only 0.136 N×m. It is obviously valid to neglect bearing losses in this estimate. Then, the overall efficiency of the system in a one way transfer of energy is estimated as the product of the efficiencies of the gear meshes involved, which include two bevel gear meshes and two helical meshes, or (0.97)2 ´ (0.96)2 = 0.867. It must be emphasized that this result, based on the presentation of a concept, is meaningful insofar as it provides support to the contention that a high efficiency is to be expected in the operation of the proposed system. A more refined calculation of efficiency based on a detailed simulation would be justified on the basis of a detailed design.
5. An Alternative Pulley Arrangement
In order to reduce the space requirements of the proposed system, an alternative more compact arrangement, depicted in Figure 7, was conceived. In this arrangement, the pulleys, instead of lying in one plane, are stacked,
![]()
Figure 7. Alternative pulley arrangement.
and the portion of cable between the pulleys winds around three small idler pulleys as shown schematically in Figure 7. Which arrangement option is more appropriate would depend on considerations pertaining to a particular design.
6. Conclusions
The proposed system offers a simple, direct method for transferring a vehicle’s kinetic energy to a flywheel and vice-versa. Although the concept has not yet been tested experimentally, a high efficiency, estimated at 86.7% for one way transfer of energy in an illustrative example, is to be anticipated on the basis of the well established performance levels of the mechanical components employed. One obvious limitation is that the vehicle’s acceleration/deceleration provided by the system at any moment depends only on the vehicle’s velocity and flywheel speed and cannot be varied at will. Thus, if the demand for acceleration is less than the acceleration that the system would provide at that moment, the flywheel system is not brought into operation. On the other hand, if the demand is higher, the system is activated and the additional acceleration required is provided by the engine. Likewise, if the demand for deceleration is less than what the system would provide, the dissipative brake is used exclusively, and if greater, the system is activated and complemented by the dissipative brake.
The dynamic analysis presented establishes the differential equations governing the transfer of energy from flywheel to vehicle and vice-versa, and may be used as a basic tool in the design of a working prototype.
Acknowledgements
The author is indebted to German Carmona, Francisco Godinez and Francisco I. Lopez for their valuable assistance in preparing the paper.