1. Introduction
Piperazine-N,N′-bis-2-hydroxypropanesulfonic acid (POPSO sesquisodium salt) is a water soluble solid of considerable interest as a physiological buffer [1] for the control of pH between (7.0 and 8.5). Very recently, we have reported the values of the second dissociation constant (pK2) of 2,2-bis(hydroxymethyl)-2,2′,2″-nitrilotri- ethanol (BIS-TRIS) [2] , N-(2-acetamino)-iminodiacetic acid monosodium (ADA) [3] and monosodium 1,4-pi- perazinediethanesulfonate [4] from (278.15 to 328.15) K. Hetzer et al. [5] have determined pK2 values of PIPERAZINE, the parent compound of (POPSO), from (273.15 to 323.15) K. Thiel et al. [6] did not provide any pK2 value for (POPSO) but they did study the effect of pH on the variation of enzyme activity and growth of bacterial strain with some zwitterionic buffers including Good Buffer (POPSO) [1] [7] . Goldberg et al. [8] , in their comprehensive review article, reported that no accurate thermodynamic data of pK2 and related thermodynamic quantities for POPSO sesquisodium salt are available in literature. They also recommended (POPSO) buffer for use in the physiological pH range of 7.0 - 8.5.
We have now studied to report the values of the second thermodynamic dissociation constants of (POPSO) and the associated thermodynamic functions from (278.15 to 328.15) K. The dissociation process of POPSO sesquisodium salt is represented by
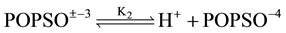 (1)
(1)
where K2 is the thermodynamic equilibrium constant. The structure of POPSO sesquisodium salt is given below:

The pK2 value of (PIPERAZINE) [5] is 9.731 and for (PIPES) it is 7.140 [4] . From the preliminary titration of POPSO sesquisodium salt with NaOH [1] , the approximate pK2 value of (POPSO) at 298.15 K is 7.785; whereas, our value from a comprehensive study is 7.803.
In order to get very accurate and reproducible pH values required for biomedical research and the calibration of the pH meter assembly with glass electrode, highly reliable pK2 values are prerequisites. The main purpose of this paper is to establish (POPSO) as a pH buffer standard for physiological use. We have undertaken to determine the pK2 values of (POPSO) at 12 different temperatures in the range (278.15 to 328.15) K employing the following galvanic cell for the electromotive-force measurements (e.m.f):
 [A]
[A]
where, for the cell A, there is no liquid junction; m1, m2, m3 indicate the molalities of the respective species; and two electrodes (hydrogen gas electrode and the silver-silver chloride) are used.
2. Experimental
Materials―POPSO sesquisodium salt was obtained from Sigma-Aldrich (St. Louis, Missouri) and was used as received. Its assay was ≥98%. The molecular formula is C20H41N4Na3O16S4 and the molecular mass is 790.79 g/mol. It is highly soluble in water. The buffer solutions were prepared from weighted amounts of CO2-free redistilled water, dried samples of NaCl, POPSO sesquisodium salt, and CO2-free standard solution of NaOH. Usually, all buffer solutions were prepared a day before the e.m.f measurements were made. Vacuum corrections were made to all masses. The ionic strength (I) range for all experimental buffer solutions was from I = 0.0354 to 0.101 mol・kg−1. The uncertainty in the concentration (molality) is estimated to be within ±0.03%.
3. Methods and Results
The method of making e.m.f measurements over the temperature range was essentially the same as that used in the study of (PIPES) [4] . At 298.15 K, the standard deviation between the initial and the middle e.m.f reading was ±0.04 mV. The preparation of the thermal electrolytic type Ag-AgCl electrode, the hydrogen electrode, the design of cells [3] [4] , and other experimental details have been described in previous publications [9] -[11] . The e.m.f values have been corrected, as usual, to the partial pressure of one atmosphere of dry hydrogen. These cell voltage values are listed in Table 1.
![]()
![]()
Table 1. Electromotive-force (e.m.f) of cell A (in volts): Pt(s); H2(g), 1 atm|Na3POPSO (m1) + Na4POPSOate (m2) + NaCl (m3)|AgCl(s), Ag(s).
The general equation for calculating the thermodynamic acidic dissociation constant, pK2, is obtained by combining the e.m.f equations (the Nernst equation for the cell) with the dissociation step (mass-law expression) of Equation (1) and with the extended form of the Debye-Hückel equation for the molal activity coefficients (γ) of all ions present in the buffer solution. The resulting equation is given below:
 (2)
(2)
whereas the last term of Equation (2) is equal to
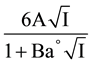 (3)
(3)
In this equation, E is the corrected e.m.f from Table 1, E° is the standard electrode potential of the cell, I is the ionic strength of the buffer solution, A and B are the Debye-Hückel constants [12] and Ba° is 1.38 kg1/2×mol−1/2 [12] for all experimental temperatures corresponding to an “ion-size parameter” a° of 4.2 A°.
In Equation (2), the “apparent” thermodynamic dissociation constant,  , becomes equal to the true pK2 (intercept) at an ionic strength (I) of zero from the linear plot of the following equation:
, becomes equal to the true pK2 (intercept) at an ionic strength (I) of zero from the linear plot of the following equation:
 (4)
(4)
in which:
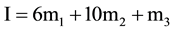 (5)
(5)
and ß is the slope parameter. The terms m1, m2, m3 correspond to the molalities of species indicated in cell A and Equation (2). The values of pK2, together with standard deviation of the intercept and also the values ß with the standard deviation of the least squares fit, are listed in Table 2.
In order to calculate the associated thermodynamic quantities for the dissociation process, the values of pK2 for 12 experimental temperatures (278.15 to 328.15) K were fitted to the following Ives-Moseley equation [13] :
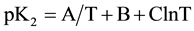 (6)
(6)
The resulting equation is:
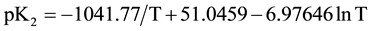 (7)
(7)
and the standard deviation of the fit is 0.0008.
By application of the customary thermodynamic relations to the constants of Equation (7), the values of the standard changes of Gibbs energy (∆G°), enthalpy (∆H°), entropy (∆S°) and heat capacity (∆Cp°) for the dissociation of one mole of POPSO±−3 in the standard state were derived. The uncertainties of these quantities were computed by the method of Please [14] . These values of the thermodynamic quantities with the standard deviations of regression are entered in Table 3. The estimated standard errors of these thermodynamic quantities are as follows: ∆G°, 5 J・mol−1; ∆H°, 34 J・mol−1; ∆S°, 0.11 J・K−1・mol−1; and ∆Cp°, 4 J・K−1・mol−1.
4. Discussion
There does not appear to be any accurate thermodynamic data in the literature for the dissociation of (POPSO). Only very preliminary data from a simple titration method [1] is available, with no mention of the ionic strength. At 298.15 K the value was reported to be 7.785 (calculated from the temperature derivative). From the precise and rigorous experimental measurements, our values of pK2 at 298.15 K from Table 2 are 7.8029 ± 0.0008. Thus, there is a significant difference between these two measurements. Also Azab et al. [15] reported the pK2 value of (POPSO) from the simple titration of (POPSO) buffer solution against KOH. Their value is 7.60 ± 0.02. This significant difference is explained. The titration method involves ion-selective electrode with a calomel reference causing a greater uncertainty in e.m.f value due to the liquid junction potential. Our method involves precise measurement using hydrogen and Ag-AgCl electrodes without liquid junction.
![]()
Table 2. Second dissociation constant of Na3POPSO from (278.15 to 328.15) K.
aStandard deviation of pK2; bSlope parameter.
![]()
Table 3. Thermodynamic quantities for the dissociation of Na3POPSO from (278.15 - 328.15) K.
Units: ∆G°, ∆H°, J・mol−1; ∆S°, ∆Cp°, J・K−1・mol−1.
It is interesting to mention that at the human body temperature of 310.15 K, our pK2 value is 7.6628. The pH of blood at this temperature is equal to 7.407. Thus, the (POPSO) buffer can be used as pH primary standard for physiological use. Moreover, the usefulness of (POPSO) and other Good Buffers [7] [9] [11] for pH control in the range of physiological interest, in the aggregation of peptides [16] and surface active behavior [17] , have been reported.
It is interesting to compare the values of the thermodynamic quantities of some structurally related zwitterio- nic buffer compounds with that of (POPSO). Such a comparison of the values at 298.15 K is summarized in Table 4. Examples of structurally similar compounds are; N-substituted amino sulfonic acids, (TABS) [9] , (MOBS)
![]()
Table 4. Comparison of the thermodynamic functions for the second acid dissociation constant of Na3POPSO with structurally related compounds in water at 298.15 K.
Units: ∆H°, J∙mol−1; ∆S°, ∆Cp°, J∙K−1∙mol−1.
[11] and (AMPSO) [10] [18] . These are the parent compounds (TAURINE) [19] , (MORPHOLINE) [20] , and (PIPERAZINE) [5] [21] , respectively. The value of pK2 of (PIPES) [4] at 298.15 K is 7.1399; whereas, that for a similar structure (POPSO) from the present study is 7.8029. It is evident that lengthening of the chain has, as expected, increased the basicity (decreased the acidity) of the NH+ group from (PIPES) to (POPSO) (this study). The enthalpy of dissociation has increased from 11,965 J・mol−1 to 19,877 J・mol−1. The increase in pK2 is usually paralleled by the increase in ∆H°. This trend is consistent with this study.
Also it indicates that there is a significant effect on the entropy of dissociation. From Table 4, the values of ∆S° at 298.15 K for (PIPES) [4] , and (POPSO) [this investigation] are: −96.5 J・K−1・mol−1 and −82.7 J・K−1・mol−1 respectively. These values are generally in qualitative agreement. The slightly less negative value of (POPSO) is consistent with the explanation for the stabilization of the solvent structure (decreased order) in the proximity of the ions H+, Na+, POPSO−4. In addition, this small change (less negative) in ∆S° (entropy of solvation of the NH+ group) is due to the effect of the successive introduction of hydroxyl group and (MORPHOLINE) compound into the ethyl groups of monosodium POPSO.
In Table 4, the values of ∆Cp° at 298.15 K for (PIPES) [4] and (POPSO) [this study] are 124 J・K−1・mol−1 and 134 J・K−1・mol−1 respectively. These results (slight increase in ∆Cp° of POPSO) suggest that the substitution and the presence of an extra monosodium POPSO molecule in POPSO disodium salt apparently have two effects: 1) progressive increasing of hydrophobic characters (tending to increase ∆Cp°), and 2) some changes in the solvation pattern, that is, progressively greater steric hindrance (tending to increase ∆Cp° value by exclusion of solvent) [22] .
It is better to point out that the interactions of NaCl with N-substituted aminosulfonic acid (POPSO) [this study] and (MES) [23] or aminocarboxylacid (TRICINE) [24] , are very complex. Thus, detailed quantitative explanations for these interactions are somewhat difficult.
5. Conclusion
For the 16 buffer solutions of Table 1, the largest difference between the final e.m.f reading at 298.15 K and that collected in the beginning was well within ±0.03 mV. The data is highly accurate and reproducible. The hydrogen and Ag-AgCl electrodes are reversible [25] without any complex formation with N-substituted amino acids. The results of pK2 and related thermodynamic functions are very reliable. Unfortunately, no thermodynamic data of (POPSO) is available in the literature for the purpose of comparison. Since the value of pK2 at 310.15 K (body temperature) of (POPSO) is 7.6628 ± 0.0008, the buffer solution of Na3POPSO and Na4POPSO would be a useful pH primary buffer standard for pH control in the region close to that of blood serum (pH = 7.407 at an ionic strength I = 0.16 mol・kg−1). Manuscript is under preparation, based on the new experimental data, for buffer solutions of Na3POPSO + Na4POPSO with and without the presence of NaCl in the physiological range of pH (7.0 to 8.5) at 12 different temperatures from (278.15 to 328.25) K.
Acknowledgements
The authors are grateful for the funding from the National Institutes of Health (NIH-AREA) under the grant 2R15GM66866-3. The content of this paper is the sole responsibility of the authors and does not necessarily represent the official views of the NIH of the National Institutes of the General Medical Science. R. N. Roy is indebted to the Hoffman Endowment Research Fund.
NOTES
*Corresponding author.