Electrochemical View of the Band Gap of Liquid Water for Any Solution ()
1. Introduction
The electronic properties of liquid water and its solutions have been studied by different research groups [1] -[9] . In particular, a density of states (DOS) in liquid water and its electronic band gap, which separates the molecular orbitals occupied by electrons from the unoccupied ones, have merited the attention for fundamental studying. They are not well understood in comparison with thermodynamics and microstructure of water but are important for understanding water as participant and medium of electrochemical reactions [2] .
The main difficulty in producing reliable theoretical predictions of the electronic properties of liquid water lies in the necessary compromise between the level of accuracy at which the system can be described and the thorough sampling of the phase-space, as required for converged computational quantities [1] . At that, the dominant view is that pure liquid water can be described as an amorphous insulator with a wide band gap, 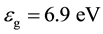 , and an electronic affinity,
, and an electronic affinity, 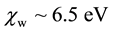 [2] .
[2] .
Several strategies have been considered to simplify the study of disordered systems: use of clusters of increasing size to model the liquid, “mean-field” approaches, use of periodically repeated small unit cells, and hybrid approaches, which use different combinations of quantum and classical methods to describe the two subsystems [1] . From uncorrelated super-molecular structure generated by the Monte-Carlo simulation, quantum mechanical calculations based on Hartree-Fock method [3] , density functional theory (DFT) with a modified functional exchange-correlation functional [4] , and ab initio molecular-dynamic simulation using DFT in the Kohn-Sham formulation with plane wave basis set [5] have been carried out to study the electronic properties of liquid water, in particular DOS and the liquid water band gap. These results [6] [7] give a large band gap as a difference between electron energies at the top of valence band and the bottom of conduction band [2] .
Allowed local electronic states have to be in the band gap of liquid water similar to impurity levels in the band gap of solid insulators occupied and not occupied by electrons [6] [8] . The most interested species of them are the occupied-by-electrons level of hydroxide ions, 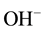 , and the vacant one of hydroxonium ions,
, and the vacant one of hydroxonium ions,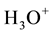 . However, the electrochemical properties of these aqueous ions have not been understood in the frame of electronic band theory so far [8] . Just filling up this gap is the subject of the present paper.
. However, the electrochemical properties of these aqueous ions have not been understood in the frame of electronic band theory so far [8] . Just filling up this gap is the subject of the present paper.
2. The Electronic Levels of Hydroxonium and Hydroxide Ions
The electronic properties of water are extremely interesting since water can influence many electrochemical processes with dissolved constituents of aqueous solution by their actively participating in these processes [1] . Perhaps the most important reaction of water is its reversible self-dissociation by emerging hydroxonium ions, 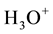 , and the hydroxide ones,
, and the hydroxide ones, 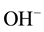 , which is described by the chemical reaction [7] [9] :
, which is described by the chemical reaction [7] [9] :
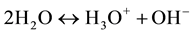 (1)
(1)
In the frame of electronic band theory, these inherent constituents of liquid water can be described as local carriers of vacant 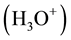 and occupied-by-electrons
and occupied-by-electrons 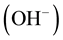 energy levels,
energy levels,  and
and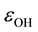 , disposed symmetrically nearby the band-gap middle which is Fermi level,
, disposed symmetrically nearby the band-gap middle which is Fermi level, ![]() , of stoichiometric water,
, of stoichiometric water, ![]() , as shown in Figure 1(a). Generally, Fermi level,
, as shown in Figure 1(a). Generally, Fermi level, ![]() , is a total electrochemical potential of water in any thermodynamic state and composition. It is a precisely defined thermodynamic quantity threshold of 50%-population of the all allowed electronic levels in the band gap of liquid water at any temperature [10] [11] .
, is a total electrochemical potential of water in any thermodynamic state and composition. It is a precisely defined thermodynamic quantity threshold of 50%-population of the all allowed electronic levels in the band gap of liquid water at any temperature [10] [11] .
As seen in Figure 1(a), the bulk electron affinity, ![]() , of stoichiometric water is equal to 6.45 eV which agrees with data [5] [6] [9] but it is considered here only as a specific case. In Figure 1(b), Fermi level,
, of stoichiometric water is equal to 6.45 eV which agrees with data [5] [6] [9] but it is considered here only as a specific case. In Figure 1(b), Fermi level, ![]() , of hypo-stoichiometric water is controlled by the electron population of the energy level,
, of hypo-stoichiometric water is controlled by the electron population of the energy level, ![]() , as a hydroxon-
, as a hydroxon-
ium-radical concentration, ![]() , where
, where ![]() is the constant of hydrated dissociation of hydro-
is the constant of hydrated dissociation of hydro-
gen molecule in water up to![]() . Opposite, Fermi level,
. Opposite, Fermi level, ![]() , of hyper-stoichiometric state of liquid wa-
, of hyper-stoichiometric state of liquid wa-
ter is controlled by hole population of the energy level, ![]() , as a hydroxyl concentration,
, as a hydroxyl concentration, ![]() ,
,
where ![]() is the constant of hydrated dissociation of oxygen molecule in water up to
is the constant of hydrated dissociation of oxygen molecule in water up to![]() . These different electrochemical states of liquid water characterize by the following standard half-reactions [12] .
. These different electrochemical states of liquid water characterize by the following standard half-reactions [12] .
![]() (2)
(2)
![]() (3)
(3)
at![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , T = 298 K [13] . Then, we have
, T = 298 K [13] . Then, we have ![]() for (2) and
for (2) and ![]() for (3) accordingly. It means that the electronic level,
for (3) accordingly. It means that the electronic level, ![]() , is mostly vacant as hydroxonium ions,
, is mostly vacant as hydroxonium ions, ![]() , due to the fixed
, due to the fixed ![]() is below
is below ![]() (see Figure 1(b), left) and the energy level,
(see Figure 1(b), left) and the energy level, ![]() , is occupied by electrons as hydroxide ions since this Fermi level is essentially above
, is occupied by electrons as hydroxide ions since this Fermi level is essentially above![]() .
.
![]()
Figure 1. Electronic band gap of liquid water for a stoichiometric state (a) with Fermi level, ![]() , in the middle of band gap and for the non-stoichiometric ones (b) with Fermi level,
, in the middle of band gap and for the non-stoichiometric ones (b) with Fermi level, ![]() and
and![]() , at confines of water stability defined by the half-reactions (2) and (3) the full blue lines denote occupied-by-electrons energy levels,
, at confines of water stability defined by the half-reactions (2) and (3) the full blue lines denote occupied-by-electrons energy levels, ![]() and
and![]() , as hydroxide ions, OH-, and hydroxonium radicals, H3O; dotted blue lines denote the vacant ones for hydroxonium ions, H3O+, and hydroxyls, OH, accordingly;
, as hydroxide ions, OH-, and hydroxonium radicals, H3O; dotted blue lines denote the vacant ones for hydroxonium ions, H3O+, and hydroxyls, OH, accordingly; ![]() is the bulk electron affinity of liquid.
is the bulk electron affinity of liquid.
The forcedly variable Fermi level, ![]() , in the band gap of liquid water is determined rigorously by the ratio of
, in the band gap of liquid water is determined rigorously by the ratio of
the concentrations: ![]() and
and![]() , as portions of vacant
, as portions of vacant ![]() and occupied by
and occupied by
electrons ![]() energy levels,
energy levels, ![]() and
and![]() , fixed in the band gap of liquid water. These proportions are given by Fermi-Dirac statistics which can be simplified to Maxwell-Boltzmann distribution of electrons and holes in the corresponding energy levels [10] [11] :
, fixed in the band gap of liquid water. These proportions are given by Fermi-Dirac statistics which can be simplified to Maxwell-Boltzmann distribution of electrons and holes in the corresponding energy levels [10] [11] :
![]() (4)
(4)
![]() (5)
(5)
where T is Kelvin temperature, and ![]() is Boltzmann constant equal to 8.62 × 10?5 eV/K.
is Boltzmann constant equal to 8.62 × 10?5 eV/K.
So, we submit the values of![]() ,
, ![]() ,
, ![]() , and
, and ![]() for half-reactions (2) and (3) in these
for half-reactions (2) and (3) in these
Equations and obtain:![]() ,
,![]() . Here, Fermi levels,
. Here, Fermi levels, ![]() ,
, ![]() , for
, for
the non-stoichiometric states of liquid water are the confines of its thermodynamic stability.
From the well known requirement of ![]() [5] , we find:
[5] , we find:![]() , and hence, the electronic energy levels of inherent water constituents:
, and hence, the electronic energy levels of inherent water constituents:
![]() (6)
(6)
![]() (7)
(7)
where ![]() (see Figure 1(a)). In changing
(see Figure 1(a)). In changing ![]() of aqueous solution, the composition deviation, x, of non-stoichiometric water,
of aqueous solution, the composition deviation, x, of non-stoichiometric water, ![]() , will be defined by equation [14] [15]
, will be defined by equation [14] [15]
![]() (8)
(8)
and one can show that the hypo-stoichiometric state, ![]() , at |x| < 10?6 is achieved in acidic solution
, at |x| < 10?6 is achieved in acidic solution
![]() easier than in the basic one
easier than in the basic one ![]() by shifting Fermi level to the conduc-
by shifting Fermi level to the conduc-
tion band.
Opposite, the hyper-stoichiometric one, ![]() , also at |x| < 10?6 is achieved in basic solution
, also at |x| < 10?6 is achieved in basic solution
![]() easier than in the acidic one
easier than in the acidic one ![]() by shifting Fermi level to the valence band.
by shifting Fermi level to the valence band.
At the same time, Fermi level is mostly sensitive to the non-stoichiometry amount, x, in the hypo-stoi- chiometric basic solution and in the hyper-stoichiometric acidic one because the concentrations of hydroxonium and hydroxide ions as inherent water species have to be in the ratio [16]
![]() (9)
(9)
with the dissociation constant Kw = 10?14 M2 at T = 298 K. Reduction-Oxidation (RedOx) potential of an aqueous solution is measured by Standard Hydrogen Electrode (SHE) with the half-reaction [12]
![]() (10)
(10)
Directly identifying this electrode by means of congruous Fermi level, ![]() , in the band gap of liquid water, we can find Fermi level,
, in the band gap of liquid water, we can find Fermi level, ![]() , for each standard aqueous electrodes using only the two fixed electronic energy levels,
, for each standard aqueous electrodes using only the two fixed electronic energy levels, ![]() and
and![]() , in the band gap of water.
, in the band gap of water.
3. Electronic Identifying Some Standard Aqueous Electrodes
For illustrating this identification, we consider the following half-reactions [12] :
![]() (11)
(11)
![]() (12)
(12)
![]() (13)
(13)
in addition to the half-reaction (10) which is characterized by ![]() and
and ![]() as it
as it
is shown above for the half-reaction (2). We obtain ![]() by substituting
by substituting ![]() and
and
![]() in the Equation (4) and find
in the Equation (4) and find ![]() using (6). Then, the RedOx of hydroxonium level is
using (6). Then, the RedOx of hydroxonium level is
![]() , which confines below RedOx variations of any strong acidic solution due to very
, which confines below RedOx variations of any strong acidic solution due to very
limited hydroxonium level population:![]() , that is illustrated by Figure 2.
, that is illustrated by Figure 2.
Similarly, we can find the RedOx of Standard Oxygen Electrode (11). Substituting ![]() and
and
![]() in the Equation (5), we obtain
in the Equation (5), we obtain ![]() and
and ![]() which
which
gives ![]() for the half-reaction (11).
for the half-reaction (11).
For (12), we also have ![]() but
but ![]() which gives
which gives ![]() according to the Equation (9). Substituting the values of
according to the Equation (9). Substituting the values of ![]() and
and ![]() in the Equation (5), we obtain εOH − εF(12) = 0.113 eV and Fermi level equal to
in the Equation (5), we obtain εOH − εF(12) = 0.113 eV and Fermi level equal to ![]() which gives
which gives ![]() for the half- reaction (12).
for the half- reaction (12).
Finally, we can find the RedOx potential of the Electrode (13) in the basic solution with ![]()
and ![]() in accordance with data for the half-reaction (2). From the Equation (9), we obtain
in accordance with data for the half-reaction (2). From the Equation (9), we obtain
![]() and
and ![]() when substitute the values of
when substitute the values of ![]() and
and ![]() in the Equation (4). Then,
in the Equation (4). Then, ![]() which gives
which gives![]() .
.
4. Discussion of Results
The electronic band structure of spatially-separated different aqueous electrodes is essentially differed from the one of an electric contact between them via an ion-exchanging membrane shown in Figure 3.
![]()
Figure 2. Electronic band gap of aqueous solution for standard hydrogen electrode (SHE) with Fermi level, ![]() , or the standard oxygen one with Fermi level,
, or the standard oxygen one with Fermi level, ![]() , as well as for half-reaction (12) and (13) with Fermi levels,
, as well as for half-reaction (12) and (13) with Fermi levels, ![]() and
and![]() , accordingly; the blue box is the valence band and the dotted one is the conduction band; the full blue lines denote occupied-by-electrons energy levels,
, accordingly; the blue box is the valence band and the dotted one is the conduction band; the full blue lines denote occupied-by-electrons energy levels, ![]() and
and![]() , for hydroxide ion, OH-, and hydroxonium radical, H3O; dotted blue lines denote the vacant ones for hydroxonium ion, H3O+, and hydroxyl, OH, accordingly.
, for hydroxide ion, OH-, and hydroxonium radical, H3O; dotted blue lines denote the vacant ones for hydroxonium ion, H3O+, and hydroxyl, OH, accordingly.
![]()
Figure 3. Electronic band-gap diagrams of standard electrodes (12) and (13) macroscopically separated (a) and electrically contacted (b) by the ion-exchanging membrane; the level, ![]() , unoccupied by electrons is denoted by the full line for hydroxide ion, OH-, and the vacant one is denoted by the dotted line for t hydroxyl radical, OH.
, unoccupied by electrons is denoted by the full line for hydroxide ion, OH-, and the vacant one is denoted by the dotted line for t hydroxyl radical, OH.
One can see that, the electrochemical cell generates the negative voltage relative to the standard hydrogen electrode when Fermi levels of these electrodes are equated. Here, in the specific case of Standard Electrodes (10) and (12), the SHE has the positive charge and the band-gap model of liquid water allows visualizing correctly the deformed electronic energy levels of aqueous solutions near the ion-exchanging membrane.
Using this method for identifying the RedOx potentials of the following half-reactions [12] :
![]() (14)
(14)
![]() (15)
(15)
we can assay the effect of ![]() in aqueous solutions. Here,
in aqueous solutions. Here,![]() .
.
From the Equation (9), we obtain![]() . In rating
. In rating ![]() for these half-reactions, we use the
for these half-reactions, we use the
exponential proportion between the values of hydrated dissociation energy of![]() ,
, ![]() , and
, and ![]() in aqueous
in aqueous
solution [13] :![]() ,
, ![]() and
and![]() . Then, we obtain
. Then, we obtain
![]() for Electrode (14). Substituting
for Electrode (14). Substituting ![]() and
and ![]() in Equation (5), it is easy to obtain
in Equation (5), it is easy to obtain
![]() and Fermi level
and Fermi level ![]() which conforms to the RedOx potential of half-
which conforms to the RedOx potential of half-
reaction (14) inasmuch as![]() .
.
Opposite, the Standard Electrode (15) of two oxidants as gaseous oxygen and liquid hydrogen peroxide is characterized by the negative effect of this combination. Indeed, for RedOx = 0.695 V of this electrode, Fermi
level is equal to ![]() that is higher than
that is higher than ![]() and
and ![]() of the
of the
mono-oxidant electrodes (12) and (14) accordingly. It implies that gaseous oxygen and liquid hydrogen peroxide force out each other from water because the actual concentration of hydroxide radicals in it as the electrode (15)
is reduced up to ![]() that is practically equal to zero for liquid water and essentially lesser than
that is practically equal to zero for liquid water and essentially lesser than
![]() for the half-reaction (12) and
for the half-reaction (12) and ![]() for the one (14). Therefore, water actu-
for the one (14). Therefore, water actu-
ally does not involve in the half-reaction (15) and free oxygen is reduced only up to hydrogen peroxide.
5. Conclusions
The liquid water is considered in the frame of electronic band theory with accentuating the guessed energy levels, ![]() and
and![]() , in the band gap for inherent constituents of liquid water as hydroxonium and hydroxide
, in the band gap for inherent constituents of liquid water as hydroxonium and hydroxide
ions![]() . Their radicals
. Their radicals ![]() are interpreted here as electron and hole population of the corresponding levels located symmetrically nearby the middle of the band gap with
are interpreted here as electron and hole population of the corresponding levels located symmetrically nearby the middle of the band gap with![]() .
.
In this model, the specific concentration of hydroxonium radicals, ![]() , in the aqueous solution at the
, in the aqueous solution at the
given ![]() determines uniquely Fermi level,
determines uniquely Fermi level, ![]() , as the electrochemical potential of water by the ratio
, as the electrochemical potential of water by the ratio
![]() or
or ![]() for the dissolved hydroxyls,
for the dissolved hydroxyls, ![]() , at the given
, at the given ![]() in the aqueous
in the aqueous
solution.
It is shown that such the variation of Fermi level allows describing the typical half-reactions and aqueous electrodes. For this, only two allowed electronic levels in the band gap of liquid water, ![]() and
and![]() , unoc-
, unoc-
cupied ![]() and occupied
and occupied ![]() by electrons are quite enough.
by electrons are quite enough.
At the same time, the forced transformation of liquid water in the hypo-stoichiometric state, ![]() for
for
example, by its electric reduction is realized when Fermi level, ![]() , is shifting to the electronic level,
, is shifting to the electronic level, ![]() , and higher. In this process, the pure liquid water is converted simply into solution of the hydrated atoms of hydrogen,
, and higher. In this process, the pure liquid water is converted simply into solution of the hydrated atoms of hydrogen,![]() .
.
Opposite, the hyper-stoichiometric water, ![]() , is characterized by shifting Fermi level to the level,
, is characterized by shifting Fermi level to the level,
![]() , and lower. In this process, the liquid water is simply enriched by dissolved hydroxyl radicals,
, and lower. In this process, the liquid water is simply enriched by dissolved hydroxyl radicals, ![]() , as
, as
dissociated and hydrated oxidants: half-oxygen, ![]() , or half-hydrogen-peroxide,
, or half-hydrogen-peroxide,![]() . It is
. It is
shown that two-oxidant solution of ![]() and
and ![]() is less effective than the mono-oxidant one.
is less effective than the mono-oxidant one.
Such theoretical approach closely relates the electrochemistry of aqueous solutions with the specification of electron population of allowed levels in the band gap of liquid water.
Acknowledgements
Author is pleased to the Russian foundation of basic research (RFBR) for supporting this work (grant # 13-08-00826a).