An Optimization Problem of Boundary Type for Cooperative Hyperbolic Systems Involving Schrödinger Operator ()
1. Introduction
The optimal control problems of distributed systems involving Schrödinger operator have been widely discussed in many papers. One of the first studies was introduced by Serag [1] , which discusses 2 × 2 cooperative systems of elliptic operator. Further research in this area developed the problem by studying different operator types (el- liptic, parabolic, or hyperbolic) or higher system degree as in [2] - [6] . Many boundary control problems have been introduced in [7] - [10] .
In [3] , we discussed distributed control problem for 2 × 2 cooperative hyperbolic systems involving Schrö- dinger operator.
Here, using the theory of [11] , we consider the following 2 × 2 cooperative hyperbolic systems involving Schrö- dinger operator:
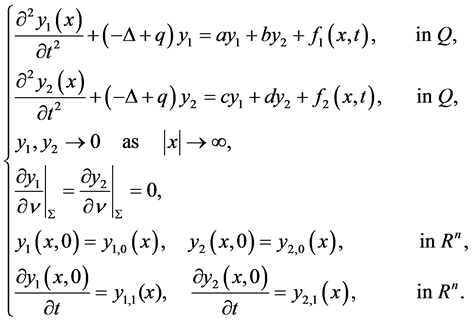 (1)
(1)
with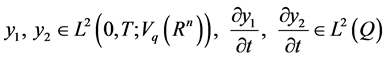 .
.
where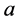 ,
,  ,
, 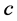 and
and  are given numbers such that
are given numbers such that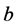 ,
, 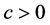 ,
,
i.e. the system (1) is called cooperative (2)
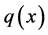 is a positive function and tending to
is a positive function and tending to 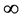 at infinity, (3)
at infinity, (3)
and 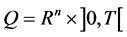 with boundary
with boundary .
.
The model of the system (1) is given by:
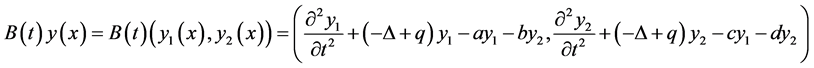
since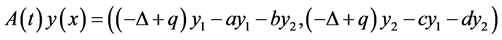 ,
,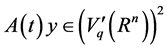 .
.
We first prove the existence and uniqueness of the state for these systems, then we introduce the optimality conditions of boundary control, we also discuss them when the observation is on the boundary.
2. Some Concepts and Results
Here we shall consider some results about the following eigenvalue problem which introduced in [1] and [12] :
![]() (4)
(4)
The associated space is![]() , with respect to the norm:
, with respect to the norm:
![]() (5)
(5)
Since the imbedding of ![]() into
into ![]() is compact, then the operator
is compact, then the operator ![]() considered as an
considered as an
Operator in ![]() is positive self-adjoint with compact inverse. Hence its spectrum consists of an infinite se- quence of positive eigenvalues, tending to infinity; moreover the smallest one which is called the principal ei- genvalue denoted by
is positive self-adjoint with compact inverse. Hence its spectrum consists of an infinite se- quence of positive eigenvalues, tending to infinity; moreover the smallest one which is called the principal ei- genvalue denoted by ![]() is simple and is associated with an eigenfunction which does not change sign in
is simple and is associated with an eigenfunction which does not change sign in![]() . It is characterized by:
. It is characterized by:
![]() (6)
(6)
We have:
![]()
which is continuous and compact.
Let us introduce the space ![]() of measurable function
of measurable function ![]() which is defined on open interval
which is defined on open interval ![]() and the variable
and the variable![]() ,
, ![]() denotes the time.
denotes the time.
On ![]() with Lebesgue measure
with Lebesgue measure ![]() we have the norm:
we have the norm:
![]()
and the scalar product
![]() ,
,
the space ![]() with the scalar product and the norm above is a Hilbert space.
with the scalar product and the norm above is a Hilbert space.
Analogously, we can define the spaces![]() ,
,
with the scalar product:
![]()
then we have:
![]()
3. The Existence and Uniqueness for the State of the System (1)
We have the bilinear form:
![]() (7)
(7)
For all ![]() the function
the function ![]() is measurable on
is measurable on![]() .
.
The coerciveness condition of the bilinear form (7) in ![]() has been proved by Serag [1] , by using the
has been proved by Serag [1] , by using the
conditions for having the maximum principle for cooperative system (1) which have been obtained by Fleckinger [13] , and take the form:
![]() (8)
(8)
that means:
![]() (9)
(9)
Theorem (3.1):
Under the hypotheses (2) and (9), if![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() , then there exists a unique solution:
, then there exists a unique solution: ![]() for system (1).
for system (1).
Proof:
Let ![]() be a continuous linear form defined on
be a continuous linear form defined on ![]() by:
by:
![]() (10)
(10)
then by Lax-Milgram lemma, there exists a unique element ![]() such that:
such that:
![]() (11)
(11)
Now, let us multiply both sides of first equation of system (1) by![]() , and the second equation by:
, and the second equation by: ![]() then integration over
then integration over![]() , we have:
, we have:
![]()
![]()
By applying Green’s formula:
![]()
![]()
By sum the two equations we get:
![]()
by comparing the previous equation with (7), (10) and (11) we deduce that:
![]()
![]()
then the proof is complete.
4. Formulation of the Control Problem
The space ![]() is the space of controls. For a control
is the space of controls. For a control![]() , the state
, the state ![]() of the system is given by the solution of
of the system is given by the solution of
![]() (12)
(12)
with![]() .
.
The observation equation is given by![]() .
.
For a given![]() , the cost function is given by:
, the cost function is given by:
![]() . (13)
. (13)
where ![]() is hermitian positive definite operator:
is hermitian positive definite operator:
![]() (14)
(14)
The control problem then is to find ![]() such that
such that![]() , where
, where ![]() is a closed con-
is a closed con-
vex subset of![]() .
.
Since the cost function (14) can be written as (see [11] ):
![]()
where ![]() is a continuous coercive bilinear form and
is a continuous coercive bilinear form and ![]() is a continuous linear form on
is a continuous linear form on![]() .
.
Then there exists a unique optimal control ![]() such that
such that ![]() for all
for all ![]() by using the general theory of Lions [11] . Moreover, we have the following theorem which gives the necessary and sufficient conditions of optimality:
by using the general theory of Lions [11] . Moreover, we have the following theorem which gives the necessary and sufficient conditions of optimality:
Theorem (4.1):
Assume that (9) and (14) hold. If the cost function is given by (13), the optimal control ![]() is then characterized by the following equations and inequalities:
is then characterized by the following equations and inequalities:
![]() (15)
(15)
with ![]()
![]() (16)
(16)
together with (12) , where ![]() is the adjoint state.
is the adjoint state.
Proof:
The optimal control ![]() is characterized by [11]
is characterized by [11]
![]() ,
,
Which is equivalent to:
![]()
i.e.
![]() (17)
(17)
this inequality can be written as:
![]() (18)
(18)
Now, since:
![]()
where
![]()
by using Green formula and (12), we have:
![]()
then
![]()
and ![]()
since the adjoint equation takes the form [11] : ![]()
and from theorem (3.1), we have a unique solution ![]() which satisfies
which satisfies![]() ,
, ![]() ,
, ![]() ,
,![]() .
.
This proves system (15).
Now, we transform (18) by using (15) as follows:
![]()
Using Green formula, we obtain:
![]()
Using (12), we have:
![]() .
.
Thus the proof is complete.
5. Formulation of the Problem When the Observation Is on the Boundary
The observation equation is given by:
![]()
![]() .
.
This is interpreted as follows [11] : we take the trace of ![]() on
on![]() , which is particular in
, which is particular in![]() . Let this be denoted by
. Let this be denoted by![]() .
.
For a given![]() , the cost function is given by:
, the cost function is given by:
![]() . (19)
. (19)
where ![]() is defined as in (14).
is defined as in (14).
The control problem then is to find ![]() such that
such that![]() , where
, where ![]() is a closed con-
is a closed con-
vex subset of![]() .
.
Since the cost function (19) can be written as [11] :
![]() ,
,
where ![]() is a continuous coercive bilinear form and
is a continuous coercive bilinear form and ![]() is a continuous linear form on
is a continuous linear form on![]() . Then using the general theory of Lions [11] , there exists a unique optimal control
. Then using the general theory of Lions [11] , there exists a unique optimal control ![]() such that
such that ![]() for all
for all![]() . Moreover, we have the following theorem which gives the necessary and suf-
. Moreover, we have the following theorem which gives the necessary and suf-
ficient conditions of optimality:
Theorem (5.1):
Assume that (9) and (14) hold. If the cost function is given by (19), the optimal control ![]()
is then characterized by the following equations and inequalities:
![]() (20)
(20)
with ![]() together with (16) and (12).
together with (16) and (12).
Proof:
The optimal control ![]() is characterized by [11] :
is characterized by [11] :
![]()
Which is equivalent to:
![]()
i.e.
![]() (21)
(21)
this inequality can be written as:
![]() (22)
(22)
since the adjoint system takes the form [11] :
![]()
and from theorem (3.1), we get a unique solution ![]() which satisfies:
which satisfies: ![]() .
.
This proves system (20).
Now, we transform (22) by using (20) as follows:
![]()
Using Green formula, we obtain:
![]()
Using (12), we have:
![]() ,
,
which is equivalent to:
![]() .
.
Thus the proof is complete.
6. Conclusions
In this paper, we have some important results. First of all we proved the existence and uniqueness of the state for system (1), which is (2 ´ 2) cooperative hyperbolic system involving Schrödinger operator defined on ![]() (Theorem 3.1). Then we found the necessary and sufficient conditions of optimality for system (1), that give the characterization of optimal control (Theorem 4.1). Finally, we also find the necessary and sufficient conditions of optimal control when the observation is on the boundary (Theorem 5.1).
(Theorem 3.1). Then we found the necessary and sufficient conditions of optimality for system (1), that give the characterization of optimal control (Theorem 4.1). Finally, we also find the necessary and sufficient conditions of optimal control when the observation is on the boundary (Theorem 5.1).
Also it is evident that by modifying:
-the nature of the control (distributed, boundary(,
-the nature of the observation (distributed, boundary(,
-the initial differential system,
-the type of equation (elliptic, parabolic and hyperbolic),
-the type of system (non-cooperative, cooperative),
-the order of equation,
many of variations on the above problem are possible to study with the help of Lions formalism.