1. Introduction
In this section we review some well-known phenomena in order to motivate subsequent developments and provide a background of the phenomena and terminology.
Volatility smiles. In a nutshell, vanilla options with different maturities and strikes have different volatilities implied by the well-known formula of [1] . Implied volatility is quoted as the market expectation about the average future volatility of the underlying asset over the remaining life of the option. Thus compared to historical volatility it is the forward looking approach.
For many years, practitioners and academics have tried to analyse the volatility smile phenomenon and under- stand its implications for derivatives pricing and risk management. In [2] , their link between the real-world and risk-neutral processes of the underlying would be complete by non-traded sources of risk. [3] found that the dynamics of the risk premium, when volatility is stochastic, is not a traded security. A number of models and extensions of, or alternatives to, the Black-Scholes model, have been proposed in the literature: the local volatility models of [4] [5] ; a jump-diffusion model of [6] ; stochastic volatility models of [7] [8] and others; mixed stochastic jump-diffusion models of [9] and others; universal volatility models of [10] - [13] and others; regime switching models, etc.
From a hedging perspective, traders who use the Black-Scholes model must continuously change the volatility assumption in order to match market prices. Their hedge ratios change accordingly in an uncontrolled way: the models listed above bring some order into this chaos. In the course of time, the general consensus, as advocated by practitioners and academics, is to choose a model that produces hedging strategies for both vanilla and exotic options resulting in profit and loss distributions that are sharply peaked at zero. We argue that a model recovered from option prices by no means explains the phenomenon.
Convexity adjustments. One of many well-known adjustments is the convexity adjustment; the implied yield of a futures and the equivalent forward rate agreement contracts are different. This phenomenon implies that market participants need to be paid more (or less) premium.
The common approach, as used by most practitioners and academics, is to adjust futures quotes such that they can be used as forward rates. Naturally, this approach depends on an model that is used for this purpose. For the extended Vasicek known as [14] and [15] model, explicit formulae can be derived. The situation is different for models whose continuous description gives the short rate a log-normal distribution such as the [16] and [17] models: for these, in their analytical form of continuous evolution, futures prices can be shown to be positively infinite [18] and [19] . In subsequent developments, we shall offer a different approach to this phenomenon.
Parallel derivative markets. In an economic system, a financial market consists of a risk-free money account, primary and parallel markets. Examples of primary markets are stocks and bonds, and examples of parallel markets are derivatives such as forward, futures, vanilla options whose values are derived from the same primary asset. Market makers can trade and make prices for derivatives in a parallel market without references to another.
The framework is as follows: a complete probability space 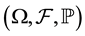 with a filtration
with a filtration 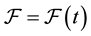 satisfying the usual conditions of right-continuity and completeness.
satisfying the usual conditions of right-continuity and completeness. 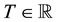 denotes a fixed and finite time horizon; furthermore, we assume that
denotes a fixed and finite time horizon; furthermore, we assume that 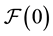 is trivial and that
is trivial and that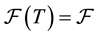 . Let
. Let 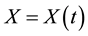 be a continuous semi-
be a continuous semi-
martingale representing the price process of a risky asset.
The absence of arbitrage opportunities implies the existence of a probability measure  equivalent to the probability measure
equivalent to the probability measure 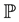 (the real world probability), such that
(the real world probability), such that  is a
is a  -martingale. Denote by
-martingale. Denote by 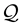 the set of coexistent equivalent measures
the set of coexistent equivalent measures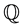 . A financial market is considered such that
. A financial market is considered such that . Uniqueness of the equivalent probability measure
. Uniqueness of the equivalent probability measure 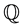 implies that the market is complete. The fundamental theorem of asset pricing establishes the relationship between the absence of arbitrage opportunities and the existence of an equivalent martingale measure and in a basic framework is proved by [20] - [22] . The modern version of this theorem, established by [23] , states that the absence of arbitrage opportunities is “essentially” equivalent to the existence of an equivalent martingale measure under which the discounted (primary asset) price process is a martingale.
implies that the market is complete. The fundamental theorem of asset pricing establishes the relationship between the absence of arbitrage opportunities and the existence of an equivalent martingale measure and in a basic framework is proved by [20] - [22] . The modern version of this theorem, established by [23] , states that the absence of arbitrage opportunities is “essentially” equivalent to the existence of an equivalent martingale measure under which the discounted (primary asset) price process is a martingale.
For simplicity, we consider only one horizon of uncertainty . A contingent claim, or a derivative,
. A contingent claim, or a derivative, 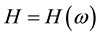 is a payoff at time
is a payoff at time![]() , contingent on the scenario
, contingent on the scenario![]() . The derivative has the special form
. The derivative has the special form ![]() for some function
for some function![]() . Here,
. Here, ![]() is referred to as the primary (or the “underlying”). More
is referred to as the primary (or the “underlying”). More
generally, ![]() depends on the whole evolution of
depends on the whole evolution of ![]() up to time
up to time ![]() and is a random variable
and is a random variable
![]() (1)
(1)
In financial terms, every contingent claim can be replicated by means of a trading strategy (or inter- changeably known as hedging strategy or a replication portfolio) which is a portfolio consisting of the primary asset ![]() and a risk-free money account
and a risk-free money account![]() . Let
. Let ![]() and
and ![]() be a predictable process
be a predictable process
and an adapted process, respectively. ![]() and
and ![]() are the amounts of asset and money account, respec-
are the amounts of asset and money account, respec-
tively, held at time![]() . In this section, for ease of exposition, we assume that
. In this section, for ease of exposition, we assume that ![]() for all
for all![]() . The value of the portfolio at time
. The value of the portfolio at time ![]() is given by
is given by
![]() (2)
(2)
for![]() . It can be shown that the trading strategy
. It can be shown that the trading strategy ![]() is admissible such that the value process
is admissible such that the value process ![]() is square-integrable and has right-continuous paths and is defined by
is square-integrable and has right-continuous paths and is defined by
![]() (3)
(3)
for![]() . For
. For ![]() -almost surely, every contingent claim
-almost surely, every contingent claim ![]() is attainable and admits the following representation
is attainable and admits the following representation
![]() (4)
(4)
where![]() . Moreover, the strategy is self-financing and its cost, namely derivative price, is a constant
. Moreover, the strategy is self-financing and its cost, namely derivative price, is a constant![]() .
.
![]() (5)
(5)
The constant value ![]() represents a perfect replication or a perfect hedge.
represents a perfect replication or a perfect hedge.
Thus far, we have presented the well-known mathematical construction of a hedging strategy in a complete market where every contingent claim is attainable. In a complete market, derivative prices are unique―no arbitrage opportunities exist. Derivatives cannot be valuated in a parallel market at any price other than![]() .
.
From financial and economic point of view, the phenomena imply that the market is incomplete, arbitrage opportunities exist and may not be at all eliminated. A derivative can be valued at different prices and hedged by mutually exclusively trading in risky assets (or derivatives) in parallel markets where market makers engage in market activities: investments, speculative trading, hedging, arbitrage and risk management. In addition, market makers expose themselves to market conditions such as liquidity, see for instance [24] . We argue that exposure to the variability of market activities, market conditions and generally to uncertain future events constitutes a basis of arbitrage opportunity, namely intrinsic risk.
In general, market incompleteness is a principle under which every contingent claim bears intrinsic risks. Let us postulate an assumption as a basis for subsequent reasonings and discussions.
Assumption. The market is incomplete and there exist intrinsic risks inherent in every contingent claim.
While the assumption is theoretical, it is rather realistically a proposition with the phenomena as proof.
In a mathematical context, let ![]() be the set of all intrinsic risks; that is the set of all real valued functions on
be the set of all intrinsic risks; that is the set of all real valued functions on![]() . Denote by
. Denote by ![]() the measure of an intrinsic risk
the measure of an intrinsic risk ![]() on the scenario
on the scenario![]() . As a measure of intrinsic risk,
. As a measure of intrinsic risk, ![]() is a mapping from
is a mapping from ![]() into
into![]() . As a basic object of our study,
. As a basic object of our study, ![]() shall therefore be the random variable on the set of states of nature at a future date
shall therefore be the random variable on the set of states of nature at a future date![]() . Generally,
. Generally, ![]() depends on the evolution of the primary asset up to time
depends on the evolution of the primary asset up to time ![]() and may also depend on the contingent claim:
and may also depend on the contingent claim:
![]() (6)
(6)
The superscript indicates the dependence of a particular contingent claim![]() . This leads to a new representation of
. This leads to a new representation of ![]()
![]() (7)
(7)
We now introduce the Kunita-Watanabe decomposition
![]() (8)
(8)
where ![]() is a square-integrable martingale orthogonal to
is a square-integrable martingale orthogonal to![]() . Thus, we have
. Thus, we have
![]() (9)
(9)
where ![]() and
and![]() . This representation of
. This representation of ![]() has been extensively dealt with, see for
has been extensively dealt with, see for
example [25] . By incompleteness, the derivative value ![]() represents a perfect hedge, which manifests an initial intrinsic value of risk
represents a perfect hedge, which manifests an initial intrinsic value of risk![]() . In relation to the hedging strategy (7), the measure of intrinsic risk shall be considered as the value of all possible future capital which, required to control the risk incurred by the market maker (such as hedger) and invested in the primary asset, makes not only the contingent claim acceptable, but also its valuation fair.
. In relation to the hedging strategy (7), the measure of intrinsic risk shall be considered as the value of all possible future capital which, required to control the risk incurred by the market maker (such as hedger) and invested in the primary asset, makes not only the contingent claim acceptable, but also its valuation fair.
From a mathematical point of view, market incompleteness implies that there exists in the set ![]() an equivalent measure, not necessarily a martingale and/or unique measure, and that is assigned to a parallel market. Thus, intrinsic risk may depend on the derivative and is not necessarily unique, as such its measure takes many forms some of which we shall consider for applications. In the remaining of this paper, we shall not discuss further on the abstract representations (7) and (9), but present them in a more descriptive (down to earth) framework―the continuous time framework.
an equivalent measure, not necessarily a martingale and/or unique measure, and that is assigned to a parallel market. Thus, intrinsic risk may depend on the derivative and is not necessarily unique, as such its measure takes many forms some of which we shall consider for applications. In the remaining of this paper, we shall not discuss further on the abstract representations (7) and (9), but present them in a more descriptive (down to earth) framework―the continuous time framework.
2. Market, Portfolio, Absence of Arbitrage and Intrinsic Price of Risk
In this section we propose a continuous time financial market consisting of a primary price process ![]() and a risk-free money account
and a risk-free money account![]() . We shall define a measure of intrinsic risk and show that perfect hedging strategies can be constructed. We also show that the existence of intrinsic risk provides an internal consistency in pricing and hedging a contingent claim.
. We shall define a measure of intrinsic risk and show that perfect hedging strategies can be constructed. We also show that the existence of intrinsic risk provides an internal consistency in pricing and hedging a contingent claim.
Let ![]() be a Brownian motion on the complete probability space
be a Brownian motion on the complete probability space![]() . The underlying price process of
. The underlying price process of ![]() satisfies the SDE
satisfies the SDE
![]() (10)
(10)
where ![]() and
and ![]() are Lipschitz continuous functions so that a solution exists.
are Lipschitz continuous functions so that a solution exists. ![]() and
and ![]() can be functions of
can be functions of![]() . The price process of
. The price process of ![]() is given by
is given by
![]() (11)
(11)
where ![]() is a Lipschitz continuous function.
is a Lipschitz continuous function.
We expand the portfolio value process (2) as follows:
![]() (12)
(12)
where ![]() is a
is a ![]() -Brownian motion and is defined by
-Brownian motion and is defined by
![]() (13)
(13)
and
![]()
Here, ![]() is some martingale measure. Indeed, the theory of the Girsanov change of measure, see for example [26] , shows that there exists such a martingale measure
is some martingale measure. Indeed, the theory of the Girsanov change of measure, see for example [26] , shows that there exists such a martingale measure ![]() equivalent to
equivalent to ![]() and which excludes arbitrage opportunities. More precisely, there exists a probability measure
and which excludes arbitrage opportunities. More precisely, there exists a probability measure ![]() such that
such that
![]() (14)
(14)
and ![]() is a
is a ![]() -martingale. Such a martingale measure
-martingale. Such a martingale measure ![]() is determined by the right-continuous square- integrable martingale
is determined by the right-continuous square- integrable martingale
![]()
for![]() . And explicitly
. And explicitly
![]()
and ![]() satisfies Novikov’s condition
satisfies Novikov’s condition
![]()
It is not hard to see that the price process ![]() under
under ![]() is given by
is given by
![]() (15)
(15)
Note that the martingale measure ![]() and
and ![]() are, if unique, theoretically and practically well-known as the risk-neutral measure and the market price of risk, respectively. The risk-neutral valuation formula is given by
are, if unique, theoretically and practically well-known as the risk-neutral measure and the market price of risk, respectively. The risk-neutral valuation formula is given by
![]() (16)
(16)
The expectation is taken under the measure![]() .
.
It is important to note that in the risk-neutral world the essential theoretical assumptions are: 1) the true price process (10) is correctly specified and 2) prices of derivatives ![]() are drawn from this price process, that is derivative prices are uniquely determined by Formula (16). These assumptions, if not violated, lead to a com- plete market and the trading strategy (12) and the measure
are drawn from this price process, that is derivative prices are uniquely determined by Formula (16). These assumptions, if not violated, lead to a com- plete market and the trading strategy (12) and the measure ![]() are unique. However, in practice as we argued earlier, these assumptions are strongly violated; as a result market completeness and uniqueness of derivative prices are no longer valid. That is
are unique. However, in practice as we argued earlier, these assumptions are strongly violated; as a result market completeness and uniqueness of derivative prices are no longer valid. That is ![]() is no longer risk-neutral, but only an equivalent measure in the set
is no longer risk-neutral, but only an equivalent measure in the set![]() .
.
We now consider the representation (7) in a continuous time framework where the measure of intrinsic risk (6) can be defined, without loss of generality, in terms of changes in values in a future time interval ![]() as follows.
as follows.
Definition. A measure of intrinsic risk in a time interval ![]() is defined by
is defined by![]() , where
, where ![]() is a continuous adapted process representing a rate of intrinsic risk.
is a continuous adapted process representing a rate of intrinsic risk.
As was represented earlier in (7), the evolution of a trading strategy shall be adaptable to adjust for the measure of intrinsic risk which can be considered an additional/less capital required in a time interval![]() , that is
, that is
![]() (17)
(17)
where ![]() is a
is a ![]() -Brownian motion and is given by
-Brownian motion and is given by
![]() (18)
(18)
and ![]() is a measure equivalent to
is a measure equivalent to![]() . Thus,
. Thus,![]() . Analogously,
. Analogously, ![]() is defined as an intrinsic price of risk.
is defined as an intrinsic price of risk.
Under ![]() measure, the price process of
measure, the price process of ![]() under
under ![]() is given by
is given by
![]() (19)
(19)
Consequently the fair value of a contingent claim is given by the formula
![]() (20)
(20)
From a pragmatic standpoint, what is needed in determining prices of derivatives and managing their risks is to allow sources of uncertainty that are epistemic (or subjective) rather than aleatory in nature. In theory, the value of a derivative can be perfectly replicated by a combination of other derivatives provided that these derivatives are uniquely determined by Formula (16). In practice, prices of derivatives (such as futures, vanilla options) on the same primary asset are not determined by (16) from statistically or econometrically observed model (10), but made by individual market makers who, with little, if not at all, knowledge of the true price process, have used their personal perception of the future. We argue further on this point as follows. If we let ![]() be the price process of a derivative in a derivative market (such as futures in particular,
be the price process of a derivative in a derivative market (such as futures in particular,
![]() , since its contract is not necessarily connected with a physical primary
, since its contract is not necessarily connected with a physical primary
asset), ![]() must have an abstract dynamics and is assumed to satisfy a SDE
must have an abstract dynamics and is assumed to satisfy a SDE
![]() (21)
(21)
where ![]() denotes a fixed time horizon larger than or equal to the maturity of any contingent claim,
denotes a fixed time horizon larger than or equal to the maturity of any contingent claim, ![]() is a Lipschitz continuous function so that a solution exists. We now show that
is a Lipschitz continuous function so that a solution exists. We now show that ![]() is a
is a ![]() -Brownian motion―the source of randomness that drives the derivative price process
-Brownian motion―the source of randomness that drives the derivative price process![]() . We introduce a change of time, see for example [27] . Let
. We introduce a change of time, see for example [27] . Let ![]() be a positive function such that
be a positive function such that
![]()
which is finite for finite time ![]() and increases almost surely. Define
and increases almost surely. Define![]() , let
, let ![]() be a replacement of
be a replacement of![]() , i.e.
, i.e. ![]() whose solution is given by
whose solution is given by
![]()
with![]() . Rearranging the drift term leads to
. Rearranging the drift term leads to
![]() (22)
(22)
where
![]() (23)
(23)
Here, we see the concurrence of the SDEs (19) and (22), the source of randomness ![]() is the very
is the very ![]() - Brownian motion (18). We have just shown that the measure
- Brownian motion (18). We have just shown that the measure ![]() is subjective in the sense that the valuation of a contingent claim is not only subjected to the dynamics of the primary asset price, but also subject to an exogenous measure of risk
is subjective in the sense that the valuation of a contingent claim is not only subjected to the dynamics of the primary asset price, but also subject to an exogenous measure of risk![]() . We shall call the measure
. We shall call the measure ![]() the risk-subjective measure. The connection between the risk-subjective measure and the risk-neutral measure described by (18) is far more precise than that found in [28] .
the risk-subjective measure. The connection between the risk-subjective measure and the risk-neutral measure described by (18) is far more precise than that found in [28] .
An important note here is that the trading strategy (17) is equivalent to the risk-free money account, that is the growth of portfolio value (2) is at the risk-free rate![]() . In terms of pricing and hedging, the presence of intrinsic risk imposes an internal consistency and implies that possible arbitrage exists in the market (the primary market and its associated derivative markets).
. In terms of pricing and hedging, the presence of intrinsic risk imposes an internal consistency and implies that possible arbitrage exists in the market (the primary market and its associated derivative markets).
3. Applications―Pricing and Hedging
In this section, we shall first discuss some problems related to asset models in parallel markets so as to provide some background for subsequent applications.
In the light of intrinsic risk, the SDE (21) in practice may represent a risky asset price process in parallel markets such as: 1) futures price process, or 2) an implied price process recovered from option prices where ![]() is the implied volatility. Attempts of recovering the implied price process were pioneered, for examples, by [29] - [32] and references therein.
is the implied volatility. Attempts of recovering the implied price process were pioneered, for examples, by [29] - [32] and references therein.
Market makers indeed have dispensed with the correct specification (10) and directly use an implied price process as a tool to prescribe the dynamics of the implied volatility surface. A practice of recovering an implied price process from observed derivative prices (such as vanilla option prices) and use it to price derivatives is known as instrumental approach, described in [33] . A practical point that is more pertinent to the instrumental approach is that the prices of exotic derivatives are given by the price dynamics that can take into account or recover the volatility smile. With reference to intrinsic risk, an implied price process is a mis-specification for the primary asset, this was discussed in [34] and was shown that successful hedging depends entirely on the relationship between the mis-specified volatility ![]() and the true local volatility
and the true local volatility![]() , and the total hedging error is given by, assuming zero risk-free rate,
, and the total hedging error is given by, assuming zero risk-free rate,
![]() (24)
(24)
Note that this hedge error resembles the term (23). Clearly, the hedging error is an intrinsic price of risk presented as traded asset in the hedging strategy (17), but not in (12).
Before we illustrate a number of applications for pricing and hedging with specific form of the measure of intrinsic risk, let us state a general result for derivative valuation.
3.1. Risk-Subjective Valuation
We have established the risk-subjective valuation Formula (20) where the risk-subjective price process is given by (19).
Theorem 1. The risk-subjective value ![]() of a contingent claim
of a contingent claim ![]() given by
given by
![]() (25)
(25)
is a unique solution to
![]() (26)
(26)
with ![]() and
and![]() .
.
Proof. The result is obtained by directly applying the Feynman-Kac formula.
We have shown that the trading strategy (17) yields the risk-free rate of return on the value of a derivative, and also the intrinsic risk is perfectly hedged by delta-hedging represented in (9) and (17).
3.2. Specifying Measure of Intrinsic Risk
As unpredictable as a market, prices in a parallel market (such as futures and corresponding vanilla options) may not be driven by the same source of randomness that drives the primary asset (such as stock and bond). Motivated by results (23) and (24), in the present framework it makes sense to formulate ![]() by an abstract form
by an abstract form
![]() (27)
(27)
where ![]() is the volatility of the underlying asset,
is the volatility of the underlying asset, ![]() the volatility of a risky asset in a parallel market. We propose that
the volatility of a risky asset in a parallel market. We propose that ![]() takes a general form of an exponential family
takes a general form of an exponential family
![]() (28)
(28)
the parameter ![]() and
and![]() . As a result, (27) is a special case.
. As a result, (27) is a special case.
Remark. While the diffusion term ![]() accounts for the distributional property of the primary asset price, the exogenous term
accounts for the distributional property of the primary asset price, the exogenous term ![]() accounts for a phenomenon such as volatility smile. The existence of intrinsic risk appears to undermine the true probability distribution of the underlying, however it emphasises its important role in determining the values of derivatives. It ensures maximal consistency in pricing and hedging contingent claims that are path-dependent/independent and particularly derivatives on volatility (such as variance swap, volatility swap). It insists on a realistic dynamics for the underlying asset as far as delta-hedge is concerned.
accounts for a phenomenon such as volatility smile. The existence of intrinsic risk appears to undermine the true probability distribution of the underlying, however it emphasises its important role in determining the values of derivatives. It ensures maximal consistency in pricing and hedging contingent claims that are path-dependent/independent and particularly derivatives on volatility (such as variance swap, volatility swap). It insists on a realistic dynamics for the underlying asset as far as delta-hedge is concerned.
3.3. Valuation of Forward and Futures Contracts
In practice, forward contracts are necessarily associated with the primary asset (such as stock and bond) and therefore their prices are determined by (16) and hedged by (12). As was illustrated in the previous section, can be determined by (20) which includes a measure of intrinsic risk, ![]() , as a convexity adjustment.
, as a convexity adjustment.
3.4. Derivatives on Dividend Paying Assets with Default Risk
Hedgers holding the primary asset in their hedging portfolio would receive dividends which are assumed to be a continuous stream of payments, whereas hedgers holding other hedge instruments (such as futures, vanilla options) do not receive dividends. In this case, ![]() can be considered as dividend yield and
can be considered as dividend yield and ![]() is the amount of dividend received in a time interval
is the amount of dividend received in a time interval![]() .
. ![]() may also be a non-negative function representing the hazard rate of default in a time interval
may also be a non-negative function representing the hazard rate of default in a time interval![]() , this well-known approach was proposed in [35] and references therein.
, this well-known approach was proposed in [35] and references therein.
3.5. Foreign Market Derivatives
Suppose that ![]() is the risk-free rate of return of a foreign money account and
is the risk-free rate of return of a foreign money account and ![]() the measure of risk that accounts for volatility smile, (26) is then a direct application to foreign market derivatives where
the measure of risk that accounts for volatility smile, (26) is then a direct application to foreign market derivatives where![]() . This is indeed the simplest application of risk-subjective valuation.
. This is indeed the simplest application of risk-subjective valuation.
3.6. Interest Rate Derivatives
As an exogenous variable to the risk-subjective price process (19), ![]() of a particular form would become a mean of reversion. This is a desirable feature in a number of well-known interest rate models such as extended model of [14] [17] model.
of a particular form would become a mean of reversion. This is a desirable feature in a number of well-known interest rate models such as extended model of [14] [17] model.
With reference to the liquidity preference theory or the preferred habitat theory of [36] , a term premium for a bond can be represented as a measure of intrinsic risk.
4. Concluding Remarks
It is well-known among both academics and practitioners that the standard complete market framework often fails, see for example [37] . Incomplete market framework becomes crucial in understanding and explaining well-known market anomalies. In this article we have introduced the notion of intrinsic risk and derived the risk- subjective measure ![]() equivalent to the real-world measure
equivalent to the real-world measure![]() , where
, where![]() . At a conceptual level, the theory of Girsanov change of measure allows us to recognise that the crucial role of
. At a conceptual level, the theory of Girsanov change of measure allows us to recognise that the crucial role of ![]() and the expectation
and the expectation
![]() are assigned to the price of a derivative (such as futures, vanilla option). In addition, the intrinsic risk as
are assigned to the price of a derivative (such as futures, vanilla option). In addition, the intrinsic risk as
a structure is what needed to be imposed on the mutual movements of the primary and derivative markets so that, at least, the pricing and hedging derivatives (such as swaps and caplets) can be undertaken on a consistent basis. Apart from such conceptual aspect, the measure ![]() does not undermine the role of the measure
does not undermine the role of the measure![]() , but contains a lot of knowledge about the primary market known at any given time
, but contains a lot of knowledge about the primary market known at any given time![]() . More precisely, the market’s expectation (often identified with prediction) in terms of a measure
. More precisely, the market’s expectation (often identified with prediction) in terms of a measure ![]() at time
at time ![]() is given by the conditional probability distribution
is given by the conditional probability distribution
![]() (29)
(29)
where ![]() is the information available given by the primary market at time
is the information available given by the primary market at time![]() , and
, and ![]() is the information generated by derivatives (such as vanilla options) with maturities
is the information generated by derivatives (such as vanilla options) with maturities![]() .
.
In view of the last financial crises, the market has evolved and there is an apparent need, both among practitioners and in academia, to comprehend the problems caused by an excessive dependence on a specific asset modeling approach, by ambiguous specification of risks and/or by confusions between risks and uncertainties. We approach the problems by presenting a continuous time framework. This framework brings unity, simplicity and consistency to two important aspects: pricing with a correctly specified model for the primary asset, and risks must be correctly understood and specified. In addition, the framework proposed in this article is rigorous in the sense that the true meanings of properties and relationships of intrinsic risk and volatility are self-consistent such that their values are not arbitrarily assigned nor should their properties be misused by ignorance.