Chebyshev Pseudo-Spectral Method for Solving Fractional Advection-Dispersion Equation ()
1. Introduction
Ordinary and partial fractional differential equations (FDEs) have been the focus of many studies due to their frequent appearance in various applications in fluid mechanics, viscoelasticity, biology, physics and engineering [1] [2] . Consequently, considerable attention has been given to the solutions of FDEs of physical interest. Most FDEs do not have exact solutions, so approximate and numerical techniques [3] [4] , must be used. Recently, several numerical methods to solve FDEs have been given such as variational iteration method [5] , homotopy perturbation method [3] [6] , Adomian decomposition method [7] [8] , homotopy analysis method [9] , collocation method [10] [11] and finite difference method [12] - [17] .
We introduce some necessary definitions and mathematical preliminaries of the fractional calculus theory that will be required in the present paper.
Definition 1
The Caputo fractional derivative operator  of order
of order  is defined in the following form
is defined in the following form
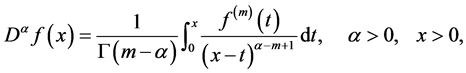
where ,
,  ,
,  is the gamma function.
is the gamma function.
Similar to integer-order differentiation, Caputo fractional derivative operator is a linear operation
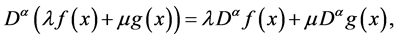
where 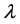 and
and 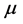 are constants. For the Caputo’s derivative we have [2]
are constants. For the Caputo’s derivative we have [2]
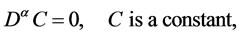 (1)
(1)
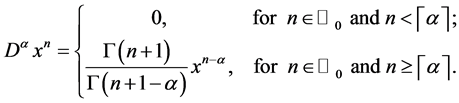 (2)
(2)
We use the ceiling function  to denote the smallest integer greater than or equal to
to denote the smallest integer greater than or equal to  and
and . Recall that for
. Recall that for , the Caputo differential operator coincides with the usual differential operator of integer order.
, the Caputo differential operator coincides with the usual differential operator of integer order.
For more details on fractional derivatives definitions and its properties see [2] .
Anomalous, or non-Fickian, dispersion has been an active area of research in the physics community since the introduction of continuous time random walks (CTRW) by Montroll and Weiss [1965]. These random walks extended the predictive capability of models built on the stochastic process of Brownian motion, which is the basis for the classical advectiondispersion equation (
ADE
).
A fractional
ADE
. is a generalization of the classical
ADE
in which the second-order derivative is replaced with a fractional-order derivative. In contrast to the classical
ADE
, the fractional
ADE
has solutions that resemble the highly skewed and heavy-tailed breakthrough curves observed in field and laboratory studies.
When a fractional Fick’s law replaces the classical Fick’s law in an Eulerian evaluation of solute transport in a porous medium, the result is a fractional ADE.
It describes the spread of solute mass over large distances via a convolutional fractional derivative.
We consider the initial-boundary value problem of the fractional Advection-dispersion equation which is usually written in the following form
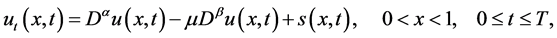 (3)
(3)
where![]() ,
, ![]() ,
, ![]() is the source term,
is the source term, ![]() is a constant and
is a constant and ![]() is the Caputo fractional derivative with respect to
is the Caputo fractional derivative with respect to ![]() and of order
and of order![]() , where
, where![]() .
.
Under the zero boundary conditions
![]() (4)
(4)
and the following initial condition
![]() (5)
(5)
In the last few years appeared many papers to study this model (3)-(5) [1] [18] - [22] , the most of these papers study the ordinary case of such problem but in this paper we study the fractional case.
Our idea is to apply the Chebyshev collocation method to discretize (3) to get a linear system of ODEs thus greatly simplifying the problem, and use FDM [12] to solve the resulting system.
The organization of this paper is as follows. In the next section, we obtain the approximation of fractional derivative![]() . In Section 3, we prove the error analysis of the proposed formula. In Section 4, we implement chebyshev collocation method to the solution of (3). As a result a system of ordinary differential equations is formed and the solution of the considered problem is introduced. In Section 5, we give some numerical results to clarify the proposed method. Also a conclusion is given in Section 6.
. In Section 3, we prove the error analysis of the proposed formula. In Section 4, we implement chebyshev collocation method to the solution of (3). As a result a system of ordinary differential equations is formed and the solution of the considered problem is introduced. In Section 5, we give some numerical results to clarify the proposed method. Also a conclusion is given in Section 6.
2. Derivation of the Approximate Formula
The well known Chebyshev polynomials are defined on the interval ![]() and can be determined with the aid of the following recurrence formula [23]
and can be determined with the aid of the following recurrence formula [23]
![]() .
.
The analytic form of the Chebyshev polynomials ![]() of degree
of degree ![]() is given by
is given by
![]() , (6)
, (6)
where ![]() denotes the integer part of
denotes the integer part of![]() . The orthogonality condition is
. The orthogonality condition is
![]()
In order to use these polynomials on the interval ![]() we define the so called shifted Chebyshev polynomials by introducing the change of variable
we define the so called shifted Chebyshev polynomials by introducing the change of variable![]() . So, the shifted Chebyshev polynomials are defined as
. So, the shifted Chebyshev polynomials are defined as![]() .
.
The analytic form of the shifted Chebyshev polynomials ![]() of degree
of degree ![]() is given by
is given by
![]() . (7)
. (7)
The function![]() , which belongs to the space of square integrable in
, which belongs to the space of square integrable in![]() , may be expressed in terms of shifted Chebyshev polynomials as
, may be expressed in terms of shifted Chebyshev polynomials as
![]() , (8)
, (8)
where the coefficients ![]() are given by
are given by
![]() . (9)
. (9)
In practice, only the first ![]() -terms of shifted Chebyshev polynomials are considered. Then we have
-terms of shifted Chebyshev polynomials are considered. Then we have
![]() (10)
(10)
Khader [24] introduced a new approximate formula of the fractional derivative and used it to solve numerically the fractional diffusion equation.
The main approximate formula of the fractional derivative of ![]() is given in the following theorem.
is given in the following theorem.
Theorem 1 [24]
Let ![]() be approximated by Chebyshev polynomials as in (10) and also suppose
be approximated by Chebyshev polynomials as in (10) and also suppose ![]() then
then
![]() (11)
(11)
where ![]() is given by
is given by
![]() (12)
(12)
Also, in this section, special attention is given to study the convergence analysis and evaluate an upper bound of the error of the proposed approximate formula.
Theorem 2 (Chebyshev truncation theorem) [23]
The error in approximating ![]() by the sum of its first
by the sum of its first ![]() terms is bounded by the sum of the absolute values of all the neglected coefficients. If
terms is bounded by the sum of the absolute values of all the neglected coefficients. If
![]() , (13)
, (13)
then
![]() , (14)
, (14)
for all![]() , all
, all![]() , and all
, and all![]() .
.
Theorem 3 [25]
The Caputo fractional derivative of order ![]() for the shifted Chebyshev polynomials can be expressed in terms of the shifted Chebyshev polynomials themselves in the following form
for the shifted Chebyshev polynomials can be expressed in terms of the shifted Chebyshev polynomials themselves in the following form
![]() , (15)
, (15)
where
![]() .
.
Theorem 4 [11]
The error ![]() in approximating
in approximating ![]() by
by ![]() is bounded by
is bounded by
![]() . (16)
. (16)
3. Procedure Solution of the Fractional Advection-Dispersion Equation
Consider the fractional Advection-dispersion equation of type given in Equation (3). In order to use Chebyshev collocation method, we first approximate ![]() as
as
![]() . (17)
. (17)
From Equations (3), (17) and Theorem 1 we have
![]() . (18)
. (18)
We now collocate Equation (18) at ![]() points
points![]() ,
, ![]() as
as
![]() . (19)
. (19)
For suitable collocation points we use roots of shifted chebyshev polynomial![]() .
.
Also, by substituting Equations (17) in the boundary conditions (4) we can obtain ![]() equations as follows
equations as follows
![]() . (20)
. (20)
Equation (19), together with ![]() equations of the boundary conditions (20), give
equations of the boundary conditions (20), give ![]() of ordinary differential equations which can be solved, for the unknowns
of ordinary differential equations which can be solved, for the unknowns![]() ,
, ![]() , using the finite difference method, as described in the following section.
, using the finite difference method, as described in the following section.
4. Numerical Results
In this section, we present a numerical example to illustrate the efficiency and the validation of the proposed numerical method when applied to solve numerically the fractional Advection-dispersion equation. Consider the ADE (3) with ![]() and the following source term
and the following source term
![]() , (21)
, (21)
and the boundary conditions![]() , with the initial condition
, with the initial condition![]() .
.
The exact solution of Equation (3) in this case is
![]() . (22)
. (22)
We apply the proposed method with![]() , and approximate the solution as follows
, and approximate the solution as follows
![]() . (23)
. (23)
Using Equation (19) we have
![]() , (24)
, (24)
where ![]() are roots of shifted Chebyshev polynomial
are roots of shifted Chebyshev polynomial![]() , i.e.
, i.e.
![]()
By using Equations (20) and (24) we can obtain the following system of ODEs
![]() , (25)
, (25)
![]() , (26)
, (26)
![]() , (27)
, (27)
![]() , (28)
, (28)
where
![]()
Now, to use FDM for solving the system (25)-(28), we will use the following notations: ![]() to be the integration time
to be the integration time ![]()
![]() for
for![]() . Define
. Define![]() ,
,![]() . Then the system (25)-(28), is discretized in time and takes the following form
. Then the system (25)-(28), is discretized in time and takes the following form
![]() , (29)
, (29)
![]() , (30)
, (30)
![]() , (31)
, (31)
![]() . (32)
. (32)
We can write the above system (29)-(32) in the following matrix form as follows
![]() . (33)
. (33)
We use the notation for the above system
![]() , (34)
, (34)
where ![]() and
and ![]()
The obtained numerical results by means of the proposed method are shown in Table 1 and Figures 1-4. In Table 1, the absolute error between the exact solution ![]() and the approximate solution
and the approximate solution ![]() at
at ![]() and
and ![]() with the final time
with the final time ![]() are given. Also, in Figure 1 and Figure 2, comparison between the exact solution and the approximate solution at
are given. Also, in Figure 1 and Figure 2, comparison between the exact solution and the approximate solution at ![]() with time step
with time step![]() ,
, ![]() and
and![]() , are presented, respectively. Also, in Figure 3 and Figure 4, the behavior of the approximate solution at
, are presented, respectively. Also, in Figure 3 and Figure 4, the behavior of the approximate solution at ![]() and
and ![]() with different values of
with different values of ![]() and
and ![]() are presented, respectively. From, these figures, we can see that the behavior of the approximate solution depends on the order of the fractional derivative.
are presented, respectively. From, these figures, we can see that the behavior of the approximate solution depends on the order of the fractional derivative.
5. Conclusion and Remarks
The properties of the Chebyshev polynomials are used to reduce the fractional Advection-dispersion equation to the solution of system of ODEs which solved by using FDM. The fractional derivative is considered in the
![]()
Figure 1. Comparison between the exact solution and the approximate solution at T = 0.5 with ![]() = 0.0025; m = 3.
= 0.0025; m = 3.
![]()
Figure 2. Comparison between the exact solution and the approximate solution at T = 0.5 with ![]() = 0.0025; m = 5.
= 0.0025; m = 5.
![]()
Figure 3. The behavior of the approximate solution at different values of α at β = 0.8.
![]()
Figure 4. The behavior of the approximate solution at different values of β at α = 1.8.
Caputo sense. In this article, special attention is given to studying the convergence analysis and estimating an upper bound of the error for the proposed approximate formula of the fractional derivative. The solution obtained using the suggested method is in excellent agreement with the already existing ones and shows that this approach can be solved the problem effectively. From the resulted numerical solution, we can conclude that the used techniques in this work can be applied to many other problems. It is evident that the overall errors can be made smaller by adding new terms from the series (23). Comparisons are made between the approximate solution and the exact solution to illustrate the validity and the great potential of the technique. All computations in this paper are done using Matlab 8.