1. Introduction
There are times when queueing systems behave like fluid. A good scenario is when customers of a busy bus station experience rush hour. Therein, the scenery looks highly saturated and stable or completely unstable. Either way, the system dynamics resembles a continuous fluid flow rather than discrete. Medhi’s analogy in [1] of fluid flow of people coming out of a subway or an electric train during rush hour is similar to the example above. The wide sense approximate continuity in such traffic flows is created by the heaviness of queueing traffic into the system. Broadly speaking, a heavy traffic queueing system can be defined as a queueing system whose server occupation rate is barely less than unity and this phenomenon as Boxma et al. [2] indicates is a feature in modern communications and computer systems today. Researches have shown that early investigation in this area was carried out by Kingman [3] on a general queue called the G/G/1 and the result is referred to as central limit theorem for1 queueing theory, see Medhi [1] .
Our objective in this paper is to survey works on heavy traffic queueing systems generally in the light of both mathematical and statistical realities with emphasis on those queues supporting the diffusion approximation. This includes their distributions, analyses, modeling and application. It is anticipated that a survey of this kind will provide an excellent background in heavy traffic studies especially in packets and internet traffic prevalent in computers, communications and telecommunications systems. To achieve an optimum survey process as in this case, it is essential that one bears in mind the Poisson traffic controversy now prevalent in telecommuni- cations and computer traffic modeling not because the controversy is relevant or not, but because there are diverse opinions worthy of sharing especially as regards the new traffic models such as the self-similar model. Not only that, recent studies have shown that the Poisson based models are equally relevant and could be used to describe the internet traffic central in this controversy. For instance, Lee and Kim [4] of late have shown that at small time scales, inter-arrival times of computer protocols such as the Simple Mail Transfer Protocol (SMTP) sessions traffic for the internet are exponentially distributed and independent of each other which makes it possible to model this kind of traffic session arrivals as a Poisson process. Before then, Karagiannis et al. [5] have indicated that the observed long-range dependence in the internet traffic does not make the Poisson based models obsolete. That at a sub-second time scales, backbone traffic appears to be well described by Poisson packet arrivals and went further to provide evidence that the ongoing pattern of the internet evolution may potentially affect the future characteristics of its traffic. Similarly, Kos and Bester [6] wrote that for a traffic model to be suitable, it should be able to represent traffic with few parameters devoid of complications and intricacies. This is the point the Poisson based models exceed all other models.
Thus, in agreement with this line of research opined that in addition to self similar models, the Poisson traffic models and their assumptions will conveniently capture the internet traffic at a given time scaling and are equally relevant. The survey is organized as follows: in section 2, we survey the onset of mathematical modeling in stable heavy traffic queues. Here, stability is in the context of Whitt [7] to mean highly saturated stable systems. In section 3, an overview of the diffusion approximation is provided with focus on unstable queues, their relevant distributions and asymptotic behaviors. We also deal with characteristics such as self similarity, long-range behavior etc. that define burstiness in computer and internet traffic giving rise to recent traffic models. Sections 4 and 5 deal with issues on modeling heavy traffic queueing systems as data traffic. Here, we studied the Poisson traffic controversy and provide a summary that best fits all lines of research relative to modern day traffic modeling. In section 6, we study applications of heavy traffic systems and contributions of data traffic science to computer and telecommunication systems development and advancement. The review is concluded in chapter 7 and 8 with open problems and summaries.
2. Heavy Traffic Approximation
Heavy traffic approximation started with the work of Kingman [3] on a one-server model with a general arrival and service time distributions called the G/G/1. Kingman [3] proved that for the G/G/1 queue under heavy traffic, the waiting time distribution could be approximated by an exponential distribution. The result is called the central limit theorem for heavy traffic queuing systems given below:
Theorem 2.1
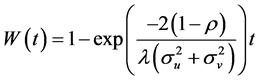 (1)
(1)
where 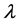 is the arrival rate,
is the arrival rate,  and
and 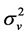 are the variances of the inter-arrival and service time distributions of customers in the system.
are the variances of the inter-arrival and service time distributions of customers in the system.
Medhi [1] noted that in 1964, Kingman made a conjecture for the seemingly more significant G/G/c queue under heavy traffic arising from developments and insights on the G/M/c model. He conjectured that the waiting time distribution in a G/G/c queue equally could be approximated similar to the G/G/1 model. Ten years later in 1974, Kollerstrom [8] proved the conjecture2 affirming that the heavy traffic waiting time distribution is of the form
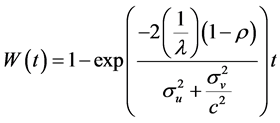 (2)
(2)
Here, 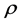 is the occupation rate and c is the number of servers.
is the occupation rate and c is the number of servers.
The two equations above represent remarkable achievements in heavy traffic analysis of modern systems with light tail or short range dependencies. Moreover, they signify outstanding developments and breakthroughs in heavy traffic approximation via classical analysis of Laplace transforms of relevant distributions as far as operations research is concerned. Apart from operational significance, the works leading to the referenced equations boasted similar works notably on the subject of convergence and behaviors of similar systems under different conditions and assumptions. Convergence here refers to convergence in distribution of sequence of stochastic queuing processes such as the arrival or service process, the waiting time or queue length process, etc, see Whitt [7] . On convergence over the years in this area, a lot has been written on queues under heavy traffic. The bulk of these works applies the diffusion approximation technique which will be discussed later in this survey on heavy traffic queuing systems. For saturated stable systems for instance, Whitt [7] noted that Borovkov [9] investigated the asymptotic behavior of a single phase case with Poisson arrival and service time distributions working independently of the service process in heavy traffic. Weak convergence limits and asymptotics for heavy traffic queues are well presented also in Borovkov [9] . Similarly, Abate and Whitt [10] studied a multi-channel queuing system and approximated the asymptotic decay rates of the queue length and the customer service distribution in form of tail probabilities under heavy traffic. The result shows that both the queue length and the service time distributions depend on the first 3 moments of their distributions. The M/G/1 queue with priority classes is an essential model giving its numerous applications. Priorities normally aroused sequel to the realistic nature of services in systems. Abate and Whitt [11] derived limit theorems for the case when the priorities are preemptive and non-preemptive with resumption tendency. They proved that in the low-priority case, the limiting waiting-time distribution is a geometric random sum of independent and identically distributed random variables similar to the M/G/1 first come first served (fcfs) waiting-time distribution. On the asymptotic behavior of tail probabilities for this model, Abate and Whitt [11] added that there is routinely a region such that the tail probabilities have non-exponential asymptotics even if the service time distribution is exponential. In addition, the asymptotics formed tend to be determined by the non-exponential asymptotics for the high-priority busy-pe- riod distribution.
Essentially, heavy traffic approximations in queues under the classical procedures are difficult especially for multi-channel queues that functions as integrated systems. These queues formed the bulk found in present day computers, communications and telecommunication systems. As Whitt [7] posited, it is not easy to work with triple or quadruple transforms and this makes it hard to obtain knitted results. Consequently, we observed two implications out of this limitation. First, attention was like shifted to obtaining other forms of approximations among others; the diffusion approximation which describes a queuing process as a Brownian motion and appears suitable for describing heavy traffic systems, see Medhi [1] . Secondly, asymptotics of similar models for instance the M/G/c and the M/M/c that seemed more realistic were attempted and derived. On the latter for instance, Boxma et al. [2] derived the asymptotics for the heterogeneous server M/G/2 with an exponential and a general server of regular variation and a cumulative service time distribution denoted by B(t). By regular variation, we mean a distribution whose compliment can be approximated by a slowly varying process at infinity index. The M/G/2 model of Boxma et al. [2] is simply the trivial prototype of a discrete channel system with two distinct service processes arising from two servers such that the regularly varying component keeps changing, making its complimentary distribution fatter as time grows large. Boxma et al. [2] have shown that such a model under light traffic is asymptotically similar to the Kingman’s solution distribution (waiting time distribution is semi-exponential distribution). However, under heavy traffic the regularly varying nature of the service time distribution of the general server will have a long tail effect on the complementary waiting time distribution of customers in the system. The Boxma et al. [2] asymptotic result for the model in question under heavy traffic is summarized in the theorem below:
Theorem 2.2
Suppose  and B(t) is the service distribution of customers served by the regularly varying general server at index –v with mean β. If L(t) is a slowly varying function on some neighborhood such that
and B(t) is the service distribution of customers served by the regularly varying general server at index –v with mean β. If L(t) is a slowly varying function on some neighborhood such that

Then the complementary waiting time distribution denoted by 1 − W(t) is given by;
 (3)
(3)
where  is the probability that there are exactly i-customers in the system at a steady time
is the probability that there are exactly i-customers in the system at a steady time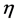 . From the above result, a sufficient condition for defining heavy tail phenomena in the M/G/c model generally under heavy traffic is evident. It is summarized in the lemma below
. From the above result, a sufficient condition for defining heavy tail phenomena in the M/G/c model generally under heavy traffic is evident. It is summarized in the lemma below
Lemma 2.1
A sufficient condition for heavy tail phenomena in a heavy traffic M/G/2 model is that, either/both the arrival or service process of customers in the system is/are significantly regularly varying at a known index as time grows large.
Remark 2.1
It is trivial since regularly varying distributions are subclass of heavy tail or more precisely, sub-exponential distributions. The light proof (by simple argument) of the lemma follows.
Proof
Given that server-1 is exponential and server 2 is general with a regularly varying distribution B(t). Then
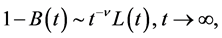 where L(t) is a slowly varying function such that
where L(t) is a slowly varying function such that
 (4)
(4)
If L(t) is undominatedly non-decreasing, we have 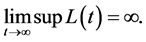 So that the open set of service times on
So that the open set of service times on
server 2 is trivially sub exponential. Similarly if L(t) is dominatedly non-decreasing and , then 1 − B(t) is open in
, then 1 − B(t) is open in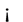 . Though, finite for a given supreme point, may be long-tailed if the supreme value is closely to infinity. This suffices. The other case follows with similar argument.
. Though, finite for a given supreme point, may be long-tailed if the supreme value is closely to infinity. This suffices. The other case follows with similar argument.
Significance here is statistical and implies relativeness with the other component. On the consequence of the former limitation, Medhi [1] indicated that researchers were motivated to seek other approximation techniques. This quest gave birth to the diffusion approximation prevalent in queuing system modeling today. Essentially, the motivation leading to the above results and many others came from the works of Kingman and others on the asymptotic behaviors of queuing systems under heavy traffic.
3. The Diffusion Approximation
The diffusion approximation in heavy traffic queuing systems came to light in the works of Iglehart [12] , Gaver [13] and Newell [14] . It consists basically two conceptually different kinds of approximations; the diffusion limits for queues justified by heavy traffic limit theorems for unstable queues and the diffusion models as continuous approximations for stable queues, see Kimura [15] . The technique involves approximating the limit of a sequence of stochastic queuing variables as a Brownian motion (diffusion). By a Brownian motion we mean a continuous time stochastic process satisfying the Markov and Gaussian properties respectively. Iglehart [12] established the first limit theorem for the palm model via this technique and Gaver [13] considered it on certain congestion problems in 1968; see Guadong et al. [16] and Medhi [1] . Similarly, Newell [14] applied the diffusion approximation on queue length distributions of certain queuing systems under heavy traffic. The idea covering the diffusion approximation is approximating the already randomized and discrete-natured queuing arrivals and departures as continuously non randomized processes analogous to fluid flow in and out of a reservoir. Then the asymptotic behavior of a queue will only involve deriving a functional law of large numbers or a functional central limit theorem.
3.1. Suitability and Robustness
Early works involved providing justifications on the suitability of the diffusion approximation in the light of analytical and numerical considerations of various queuing processes. For instance in 1970, Iglehart and Whitt [17] justified the suitability of the diffusion approximation by establishing a limit theorem for the G/G/c queue. It was proved that both the queue length and the waiting time distributions could be approximated by a Brownian motion. In 1974, Reiser and Kobayashi [18] studied the accuracy of the diffusion approximation on some networks of queuing systems. Network analysis appeared challenging given its complexities especially through classical approaches. The accuracy was considered for wide classes of distributional form of inter arrival and service times for various models. Reiser and Kobayashi [18] concluded similar to Iglehart and Whitt [17] that the diffusion approximation is quite adequate in most cases, more adequate than the exponential server model prevalent in computer system modeling.
The subject of control especially in multi-server queuing systems is a tool for describing suitability on a model resulting from smoothness in behavior either in transient or limiting case. Rami et al. [19] studied a controlled multi server queuing system restricted in the Halfin-Whitt regime, a heavy traffic regime where quality and efficiency are assured. They derived a diffusion model with a singular control term that describes the scaling limit of the queuing model. The singular term constrains the diffusion to adapt to certain subsets for any time t in the neighborhood of![]() . In addition to providing null-controllability conditions for this model, they have shown that an analogous asymptotic result holds for such multi-server systems via the diffusion approximation. Similarly, Lee and Werasinghe [20] analyzed a sequence of single-server queuing systems with impatient customers under heavy traffic. Customer impatience in form of abandonments or reneging is a significant feature of queuing systems arising from long queues upon entry. They proved that the drift coefficient of the limiting diffusion (the mean) is influenced non-linearly by the sequence of patience-time distribution. In addition, both the queue length and the waiting time processes have stable limiting distributions. The relationship between the drift coefficient and the diffusion parameter of a diffusion process is approximately linear. Wagenmakers et al. [21] studies on the mean and the variance of a diffusion model for sojourn times has shown that within the range of plausible values, the relationship between the two is linear.
. In addition to providing null-controllability conditions for this model, they have shown that an analogous asymptotic result holds for such multi-server systems via the diffusion approximation. Similarly, Lee and Werasinghe [20] analyzed a sequence of single-server queuing systems with impatient customers under heavy traffic. Customer impatience in form of abandonments or reneging is a significant feature of queuing systems arising from long queues upon entry. They proved that the drift coefficient of the limiting diffusion (the mean) is influenced non-linearly by the sequence of patience-time distribution. In addition, both the queue length and the waiting time processes have stable limiting distributions. The relationship between the drift coefficient and the diffusion parameter of a diffusion process is approximately linear. Wagenmakers et al. [21] studies on the mean and the variance of a diffusion model for sojourn times has shown that within the range of plausible values, the relationship between the two is linear.
In the 1980’s, with the advent of the facsimile (fax) machine and the internet in the years preceding the facsimile, the nature of system traffic changed tremendously. Data traffic of the internet age replaces the voice traffic of the telephone age. This shift creates most research interest in heavy traffic queuing studies via the diffusion approximation and since then, several models have been developed to approximate performance of systems such as tail probabilities, moments and distributions.
3.2. Limiting distributions
As indicated earlier, recent research focus in heavy traffic queuing systems is in the study of tail behaviors of queues in form of limiting and extreme value distributions for various models. For instance, Glynn and Whitt [22] proved the extreme value limit theorem for heavy traffic queues with general arrival and service time distributions called the G1/G/1. Using strong approximations under regularity conditions, the extreme waiting time among n-sized customers was derived. The number of customers in the system is assumed increasing as time grows large. It was shown that, when the traffic intensity ![]() approaches 1 from the left and n approaches infinity at a suitable rate, the normalized maximum wait among n-customers converges to the Gumbel extreme-value distribution. Also, Glynn and Whitt [22] added that the normalization depends only on the means and the variances of the inter arrival and service time distributions. On the contrary, if
approaches 1 from the left and n approaches infinity at a suitable rate, the normalized maximum wait among n-customers converges to the Gumbel extreme-value distribution. Also, Glynn and Whitt [22] added that the normalization depends only on the means and the variances of the inter arrival and service time distributions. On the contrary, if ![]() is a fixed point, then the maximum waiting time fails to converge to the Gumbel distribution. The General Gumbel probability distribution for a continuous random variable W(t) is given by
is a fixed point, then the maximum waiting time fails to converge to the Gumbel distribution. The General Gumbel probability distribution for a continuous random variable W(t) is given by
![]() (5)
(5)
In addition, the Gumbel extreme value distribution holds for the queue length distribution. The lemma below summarizes the ![]() region of convenience for the Gumbel distribution in the G1/G/1 model.
region of convenience for the Gumbel distribution in the G1/G/1 model.
Lemma 3.1
In a heavy traffic G1/G/1 queue under regularity conditions, if ![]() approaches one from the left origin and n steadily increases to
approaches one from the left origin and n steadily increases to ![]() then, the Gumbel distribution sufficiently model the extreme value limit of the waiting time or the queue length distribution of customers in the system.
then, the Gumbel distribution sufficiently model the extreme value limit of the waiting time or the queue length distribution of customers in the system.
Similarly, Szczotka and Woyczynski [23] studied the G/G/1 queues with service and/or the inter arrival times of heavy tailed probability distributions. Szczotka and Woyczynski [23] obtained that the waiting time distribution is exponential if the tail of the distribution of inter arrival times is heavier than that of the service times and is non-exponential in the opposite case. In other words, if the service times have a heavy-tailed distribution heavier than that of the inter arrival times in the domain of attraction of a Levy process then, the limiting distribution is a Mittag-Leffler distribution. In addition, Szczotka and Woyczynski [23] emphasized that under these modeling conditions, the queue length distribution can be analyzed. Limic [24] studied the heavy traffic behavior of a G/G/1 Last-in-First-Out (LIFO) preemptive resume queue and derived a diffusion approximation for the model. Limic [24] showed that the queue length process exhibits perhaps an unexpected heavy traffic behavior. In addition, the diffusion limit depends on the type of arrivals and services in a fairly intricate way which is related to the Wiener-Hopf factorization for random walks. Earlier in 1999, in their heavy traffic analysis of the G1/G/1 queue with heavy tailed service or arrival distribution of the regularly varying type, Boxma and Cohen [25] have shown that if the traffic intensity of the G/G/1 system approaches unity and the tail of the service distribution is heavier than that of the arrival distribution, the stationary actual waiting time distribution together with a contraption factor is a function of the traffic load and converges to the Kovalenko distribution. In contrast, if the reversed is the case and all other factors kept constant, the stationary actual waiting time distribution will still depend on the traffic load but converge to the negative exponential distribution. Hence, limiting distributions of queuing systems to a large extend depend on the model constructed. Moreover, a slight variation of significant parameters may shift distribution of systems.
Whitt [26] has provided a summary of functional limit theorems for both noisy and non-noisy single server queues. By a noisy queue we mean a queuing system with a measurable diffusion component. Using the open mapping theorem, Whitt [26] indicated that similarly to the convergence of stochastic functions to reflected Brownian motion as captivated by Donsker theorem, a discrete-time queuing model with cumulative net-input process of stationary increments and jumps of infinitesimal variance or mean will converge to a reflected stable process such as the Gaussian or the Lévy process. More explicitly, for a sequence of queuing models (multi-server systems), the limit is strictly a reflected Lévy process. Finally, Whitt [26] established that the functional central limit theorem for the customers in the queue when the input process is a superposition of many independent processes with complex dependence is a Gaussian process. Kruk et al. [27] presented a heavy-traffic analysis of a single-server queue under a scheduling policy called Earliest-Deadline-First (EDF). In this queuing discipline, customers have deadlines and are served until their deadlines elapse. The system performance is measured by the fraction of reneged work shown to be minimized by the service policy. The evolution of the lead time distribution of customers in the queue is described by a measure-valued process. It was shown that, in the heavy traffic regime, the limit of this (properly scaled) process is a deterministic function of the limit of the scaled workload process. In addition, the limit is a doubly reflected Brownian motion. The polling system queue3 where a single server revisits the queuing system in a cyclic order has also been studied and limiting distributions analyzed especially relative to unfinished jobs. For instance, the work of Coffman et al. [28] on polling queues under the exhaustive-service discipline is worthy of mentioning. Coffman et al. [28] showed that under the standard heavy traffic scaling, the total unfinished work in the system tends to Bessel-type diffusion in the heavy-traffic limit. What all these results signify in essence is that, limiting distributions of unstable (random) queuing systems are themselves stable.
4. Modeling in Network Queues
Heavy traffic analysis of network queues especially, multi class networks are gaining grounds recently. This is not unconnected with its numerous importance. Kimura [15] pointed out that multi-dimensional extension of server stations analysis is a natural diffusion model for a network of queues in computer systems. Similarly, Bertsekas and Gallagher [29] wrote that multi class network queues are used in analyzing problems of congestions and delays in computer systems, communication and complex productive systems. Their importance cannot be over emphasized. Unfortunately, several studies for instance have shown that not all multi class networks especially those with feed backs under heavy traffic can be approximated using the reflected Brownian motion see Williams [30] . However, the open multi class type under heavy traffic supports the diffusion approximation. Already, Reiser and Kobayashi [18] in the 70’s have proved that network measurements via the diffusion approximation are quite adequate. Williams [30] studied a multi class open queuing network using the semi martingale Brownian motion process and provides sufficient conditions for which heavy traffic limit theorem holds for such queues, see Williams [30] for details. Similarly, Dai and Dai [31] studied an open queuing network with finite buffers consisting of d-finite server stations. Given that a server stops working when the downstream buffer is full and all customers served at a station are homogeneous in terms of service requirements and routing. They proved that the normalized d-dimensional queue length process converges in distribution to a semi martingale reflecting Brownian motion in a d-dimensional box under a heavy traffic condition. Pekoz and Joglekar [32] considered a ./G/k finite buffer queue with a stationary ergodic arrival process and a general service with delayed feedbacks and obtained that under certain mild conditions, the feedback flow of the class of customers re-entering the queue converges to the Poisson distribution when the delay waiting time distributions is scaled up. Similar studies on the network queues followed these developments especially via the martingale representations for limiting distributions of many server systems. Already, researches have shown that the reflected Ornstein-Uhlenbeck, the geometric Brownian motion, the reflected Levy and the reflected affine diffusion processes could be used to model successfully queuing systems with noisy processes such as reneging, balking and shunting process which are in effect measurable noises4, see Ward and Glynn [33] and [34] . Guodong et al. [16] worked on the Palm model and a finite capacity M/M/N/Mn + M model with reneging via the martingale diffusion approach and provided limit proofs for the heavy traffic approximations of the queue length distribution. The martingale approach applied on the queue length process of customers involves random time changes and random thinings of the stochastic queue length process. They established a key central limit theorem and a key functional weak law of large numbers for the Palm model and the finite capacity M/M/C model respectively. The result shows that the limiting queue length distribution in both models is a reflected Ornstein-Uhlenbeck diffusion process, an adapted stochastic process in which the stochastic variable changes more with time in addition to a finite variation component of the process. It is worthy to note that the shape of the reflected OU-graph to a greater extend depends on the initial customer size at time zero.
5. Modeling Heavy Data Traffic
Modeling in heavy data traffic queuing systems is challenged by two important factors; the nature of data traffic itself and model selection. The former creates a controversy that saddles on the later. Researches on internet and telecommunications traffic processes revealed that data traffic is characterized by properties such as regular variation, long-range dependencies, self-similarity and heavy tail distributions see Leland et al. [35] , Park et al. [36] and Stralka et al. [37] . Long-range dependency and self-similarity in essence are associated with heavy tail distributions. The combination of the two defines how burst a traffic system is. A heavy data traffic process may be bursty or not depending on the time scales it is considered. Though, Medhi [1] wrote that a self-similar process arising from long-range dependent process like the internet traffic decays much slower than the exponential distribution in addition to a hyperbolic decay of autocorrelations, this does not render the Poisson traffic models that is non-bursty inadequate or better still out of the internet domain as some researches tried to portray.
The Poisson Traffic Arguments: The Bouncing Back
Since the pioneering works of Leland et al. [35] , Willinger and Paxson [38] and many others on the new network traffic description that appeared alternatives to the Poisson models, it appears the Poisson distribution has lost its place as a suitable distribution for describing the internet traffic today. Amidst its advantage, history and effectiveness, a lot has been published about its inadequacy without attending to scaling issues in both time and space. For instance in 1994, Leland et al. [35] using long, high resolution traces of Ethernet packets indicates that arrival rates of the Internet Protocol (IP) packets on a Local Area Network (LAN) exhibit not Poisson but self-similar behavior. However, similar studies have shown that within a given time scale, the two traffic networks coexist together. For instance, Boxma and Cohen in [25] observing the plots of Ethernet traffic measurements on LAN of Willinger et al. [39] , WAN of Paxson and Floyd [40] and VBR (Variable-Bit Rate) of Beran et al. [43] , Boxma and Cohen [25] watched that bursty sub periods are alternated by less bursty sub periods in each of these traffic processes indicating the coexistence of the Poisson traffic and self-similar traffic processes. Similarly, Karagianis et al. [5] have shown that there exist a Poisson process and a long range dependence in heavy Internet backbone traffic. Furthermore, Karagianis et al. [5] indicated that the User Datagram Protocol/ Transmission Control Protocol (TCP/UDP) packets obey a Poisson process at sub-second time scales while they are long range dependent at large time scales. This suggests that relatively simple statistical theories of the Poisson process can still be applicable to the design and optimization of the internet. Similarly, Lee and Kim [4] proved that at small time scales, inter-arrival times of protocols such as the simple mail transfer protocol (smtp) is a Poisson process. Finally, Karagiannis et al. [5] have shown that the mighty internet traffic in the center of this controversy at sub-second time scales appears well described by Poisson packet arrivals and evident that, the ongoing pattern of Internet evolution may eventually renewed its Poisson tendencies even for the super second time scale. Time scaling factor appears to be a decisive factor in defining suitability in this modeling case. Consequently, the below lemma follows:
Lemma 5.1
The necessary and sufficient condition for the internet traffic or a similar process to fit in the Poisson process is that, the time scaling is sub-second.
Consequently, modeling in the heavy traffic sense may well be done with the Poisson model at sub-second time interval and at large time scales, modern day data traffic models such as the self-similar model that can capture important features such as traffic burstiness with long tail distributions are effective.
6. Applications
The role heavy traffic analysis plays in the development and advancement of service systems especially computing and telecommunications systems cannot be over emphasized. Initially, even the work of Kingman on the asymptotic waiting time distribution in a G/G/1 queue is a modeling of delay time distribution in a general service system just about to reach its service capacity. In heavy traffic analysis, any limit theorem derived is to provide understanding and approximation of distributions and tail behavior of measures for bettering performance of service systems. The general motive is advancement of corresponding service systems and application depends on the reality of model. For instance, heavy traffic analysis of networks queues of various priorities is for problem analysis of modern systems. As Bertsekas and Gallagher [29] indicated; such models are used in analyzing problems of congestions and delays in computer systems, communications and complex productive systems. Priority queuing analyses and those with service interruptions may be classical models of computer systems. In the context of queuing synthesis, as Kimura [15] indicated; diffusion models are for reliability and control problems in computer and telecommunication systems. Without such analysis, problems such as those mentioned could have down our systems. The processor sharing discipline queues are used in modeling time-sharing protocols in computer systems. High speed wireless networks carrying multimedia applications under long range dependence and heavy tailed properties are troubled by excess usage. Buche et al. [41] indicated that heavy traffic analysis of long range dependence in wireless internet traffic provides relief to troubles such as large file sizes downloads from the internet and multimedia applications for instance streaming a video. The processor sharing models such as those studied in Kleinrock [42] and Ritchie and Thompson [44] in the 70's and more recently, the limited processor model of Zhang and Zwart [45] has been widely used in the analysis of computer systems, network servers and data transmission over the internet. Kruk et al. [27] indicated that in the last decade, substantial attention has been paid to queuing systems in which customers have deadlines for service in heavy traffic (EDF queues). These types of queuing models feature in telecommunication systems carrying digitized voice or video traffic, tracking systems and real-time control systems. In the case of voice or video traffic, the packet information must be received, processed and displayed within stringent timing bounds so that the integrity of the transmission is maintained. Similarly, there are processing requirements for tracking systems that guarantee that a track can be successfully followed. Real-time control systems for instance, those associated with modern avionics systems, manufacturing plants or automobiles also gather data that must be processed within stringent timing requirements in order for the system to maintain stability or react to changes in the operating environment. Another class of heavy traffic queuing models of varied applications is the polling models. Levy and Sidi [46] indicated that these models were first introduced in 1970 precisely when the cyclic queues where used in modeling time allocations in computer systems. In these models, queues are visited by a single server in a cyclic discipline. Such models are applied in the performance analysis of communication systems such as token rings and packet switches, where a single server resource is shared among many traffic stream demands on the resource, see Coffman et al. [28] . In addition, Levy and Sidi [46] provided more areas of applications of polling queues in heavy traffic to include random access protocols of computer systems, robotics and manufacturing systems. In other fields such as transportation, where heavy traffic analysis has several applications, the work of David et al. [47] on the diffusion modeling of an airport queue is an excellent use of modeling via diffusion approximation in the transportation sector. Other relevant areas of application of the heavy traffic modeling in approximations queuing systems include the repairman problem etc. Already, the works of Iglehart [12] in the 60’s has derived a diffusion limit approximations for several server case.
7. Open Problems
In all, one can identify the following areas as open problems for further research in heavy traffic queuing modeling and analysis:
1) On waiting time analysis in multi-server queues of computer and telecommunication systems.
2) Design of new queuing models that captures wide range of service systems with less complicated mode of analysis.
3) Analyzing queuing systems with similar structures as the one discussed in this review with essentially higher degree of control of system processes.
4) Designing new queuing schedules to describe service processes and routings of new or existing models and analyzing the behaviors and performance of models
8. Conclusion
In this article, mathematical modeling in heavy traffic queuing systems is generally surveyed. Initially, the onset of modeling in heavy traffic queues and asymptotic behaviors for different models were reviewed and distributions uncovered. We also looked at the diffusion approximation as a remedy to queuing analysis and approximations. Modeling both in network and heavy traffic data systems and matters arising from the internet and telecommunication traffic modeling via Poisson models and assumptions were studied and a justification on the suitability of the Poisson arrival process in addition to the new network traffic in capturing the internet traffic was supported. Finally, we provide real areas of application of heavy traffic models developed for the benefits of service systems.
Acknowledgements
The authors are grateful to Prof. Sivasamy, R., of the Statistics Department, University of Botswana for his suggestions, corrections and editing this article. Also, to the anonymous reviewer(s) of this article to this stage and to all authors of the literature reviewed in this work.
NOTES
*Corresponding author.
![]()
1This expository paper is a component of a Doctoral research Literature Review process in Queuing Systems with Heterogeneous Servers.
![]()
2Sulaiman Sani is currently a PhD student in the Dept. of Mathematics, University of Botswana-Gaborone. His area of research is in Queuing Systems with Heterogeneous Servers. Onkabetse A. Daman is a Senior Lecturer and the current head of the Dept. of Mathematics, University of Botswana-Gaborone. His field of Interest is stochastic processes, Analysis and Applications. He supervises this research work.
![]()
3Another interesting queue to model under distinct structuring.
![]()
4The two references above are good examples of works on modeling via the O-U and similar processes in queuing systems with noisy structures.