Effect Modeling of Count Data Using Logistic Regression with Qualitative Predictors ()
1. Introduction
When manufacturing high-end goods, there is a trade-off between a high yield rate or lower fraction of nonconforming goods. A slight change in the process can drastically affect the yield rate or fraction of defective products, which results in a considerable increase or decrease in product turnover.
To develop a better process, purposeful changes should be made to the input variables of a process or production system, so that we can identify the reasons for changes in either the continuous or categorical outcomes and improve the manufacturing conditions. For this reason, it is commonplace in industry to analyze fraction data such as yield rates, percentages, and units of conforming or nonconforming product. When the input variables or regression predictors are all qualitative and the responses are countable, the data are often called categorical outcomes. Analysis of variance (ANOVA) has long been a favorite technique for investigating this type of data, as discussed in Rao [1] , Wiener et al. [2] and Toutenburg and Shalabh [3] .
Unfortunately, however, there are many cases where the fraction of nonconforming units of a product is close to zero or the yield rate of conforming units is close to one. In these cases, conventional analysis techniques often result in yield rate estimates exceeding 100%, or negative defective fraction estimates, as noted by many authors.
The drawbacks of using ANOVA for fraction data were noted by Cochran [4] . According to him, even the square-root or arcsine-square-root transformations of ANOVA-type data do not work properly. As Taguchi noted in Ross [5] , the additive property of fraction data does not hold, especially when the fraction is lower than 20% or higher than 80%. He made use of what he called the omega (Ω) transformation for data conversion. Although the omega transformation has its merits, it is not satisfactory in the statistical sense. Jaeger [6] investigated the problem from the point of view of psychological or behavioral sciences, and found that ANOVA can yield spurious results even after applying the arcsine-square-root transformation to proportional data. ANOVAs over proportions can result in hard-to-interpret results, because the confidence intervals can extend beyond the interpretable values (0 and 1). As an alternative, he recommended logistic regression models, which he called the ordinary logit and/or mixed logit models.
In order to avoid above mentioned phenomena, we had better consider the logistic transformation. Dyke and Patterson [7] appear to be the first to use a logistic transformation to analyze ANOVA-type factorial data. Many theoretical backgrounds of logistic regression for categorical data analysis (CDA) are available. Montgomery [8] , Kleinbaum and Klein [9] , and Agresti [10] discussed the theoretical background in some detail. Some dichotomous response data were touched on in Dobson and Barnett [11] and Sloan et al. [12] in relation to contingency table analysis, while some polytomous response data were dealt with in Strokes et al. [13] and Dobson and Barnett [11] .
In most cases, they dealt with quantitative explanatory variables. However, there are many cases when qualitative predictors are appropriate for modeling and analyses. Even in the comprehensive book by Agresti [10] , logistic models with categorical predictors were not fully discussed. He did mention that logistic regression should include qualitative explanatory variables, often called categorical factors. In Agresti [10] , the author touched on the ANOVA-type representation of factors and use of the logistic regression model. But the suggested model is quite limited to the case of one factor, and hence is not informative enough for practitioners who want to extend it to models of multiple factors. In Strokes et al. [13] , the authors briefly introduced model fitting for logistic regression with two quantitative explanatory variables. In our opinion, however, their parameterization is a little confusing, and the ANOVA-model like parameterization is preferable.
Fortunately, modern statistics has presented many ways of extending logistic models. In this study, we consider a binary response variable (i.e., countable or categorical) and explanatory variables or predictors with three or more levels that are qualitative or categorical. The response variable may, for example, represent the units of a product manufactured under a certain condition. When trying to determine an appropriate statistical method for analyzing countable data within categorical settings, we have excluded the ANOVA-type analyses. However, we have used an ANOVA-model like parameterization with logistic regression and qualitative predictors. First, we examined the limitations of ANOVA-type analysis in connection to the defective rate or percentage data. Second, we considered logistic regression modeling of two-way binary count data with categorical variables. Then, we examined the behavior of the logistic regression model when fitted to the two-way count data within the logistic regression framework. We investigated this as an alternative to the ANOVA-type model, in an effort to combine logistic regression and qualitative predictors.
When implementing an experiment and analyzing the results, the optimal condition is sought for by testing the significance of regression parameters, evaluating the existence of interactions, estimating related confidence intervals (CIs), assessing the difference of mean values, and so on. The significance of model parameters and fraction estimates are used by the experimenter to identify and interpret the model.
The objectives of this study can be summarized as follows:
● To extend the ANOVA models with qualitative factors to logistic models with qualitative predictors.
● To estimate the main effects and/or interactions of ANOVA-model like parameterization.
● To estimate the confidence intervals (CIs) for model parameters and fractions.
● To ensure that the CIs for fractions are appropriate (between 0 and 1).
● To discuss the interpretation of the analysis results.
We have used a simple, but real, illustrative example to explain how to test the significance of model parameters, ascertain the existence of interactions, estimate the confidence intervals, and find the difference of the mean values. We have used the SAS in Allison [14] and MINITAB [15] logistic regression program to examine the efficiency of models and demonstrate the usefulness of logistic regression with ANOVA-model like parameterization.
2. Logistic Model with Categorical Predictors
2.1. Logistic Transformation
Let 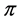 be a fraction representing the probability of the event occurring, then
be a fraction representing the probability of the event occurring, then 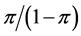 the “odds”. The naturally logged odds
the “odds”. The naturally logged odds 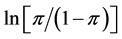 are defined as the logistic transformation and also called “logit” link function. The logit link function converts fractions
are defined as the logistic transformation and also called “logit” link function. The logit link function converts fractions  between 0 and 1 to values between minus and plus infinity. For example, if we let
between 0 and 1 to values between minus and plus infinity. For example, if we let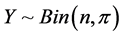 , then the random variable
, then the random variable 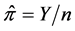 has its own probability mass function, which is discrete, non-negative, and asymmetric. The normal approximation of this random variable might cause aforementioned problems, especially when
has its own probability mass function, which is discrete, non-negative, and asymmetric. The normal approximation of this random variable might cause aforementioned problems, especially when 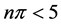 or
or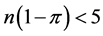 , due to the lack of normality as explained in Montgomery et al. [8] . If we take the sample log-odds
, due to the lack of normality as explained in Montgomery et al. [8] . If we take the sample log-odds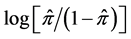 , then the shape of the distribution becomes the logistic function, which is close to the normal distribution function. The cumulative distribution function is a monotonically increasing function. For another example, Ross [5] introduced Taguchi’s omega (Ω) transformation formula in calculating db (decibel) value, which is similar to log-odds. The omega transformation formula is
, then the shape of the distribution becomes the logistic function, which is close to the normal distribution function. The cumulative distribution function is a monotonically increasing function. For another example, Ross [5] introduced Taguchi’s omega (Ω) transformation formula in calculating db (decibel) value, which is similar to log-odds. The omega transformation formula is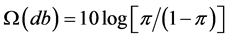 ,
,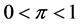 . In this study, however, only the “logit” conversion is going to be considered.
. In this study, however, only the “logit” conversion is going to be considered.
On the other hand, the logistic model is set up to ensure that whatever estimate for success or failure we have, it will always be some number between 0 and 1. Thus, we can never get a success or failure estimate either above 1 or below 0. For the variable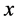 , the standard logistic response function, called
, the standard logistic response function, called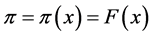 , is given by
, is given by 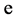 to the
to the 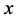 over 1 plus
over 1 plus 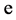 to the
to the ![]() or, alternatively, 1 over 1 plus
or, alternatively, 1 over 1 plus ![]() to minus
to minus![]() .
.
![]() (1)
(1)
For linear variety, ![]() , the logistic response function is:
, the logistic response function is:
![]() (2)
(2)
Let us think of a simple regression analysis where there exist several types of responses such as observations, regression line, confidence interval, and prediction interval. The logistic response function transforms the responses into some number between 0 and 1, which results in S-shaped curves.
Generally, for a linear predictor![]() , the logistic response function
, the logistic response function ![]() is given as:
is given as:
![]() (3)
(3)
Typical response functions with and without interaction term can be depicted as in (b) and (a) of Figure 1. The logit link function called “log-odds” and logistic response function are reciprocal to each other. The logistic model is widely used for binomial data and is implemented in many statistical programs, such as SAS and MINITAB.
2.2. Models for Two-Way Responses
Let us consider two-way ![]() layout data with
layout data with ![]() observations within each subgroup. A typical ANOVA model looks like what follows.
observations within each subgroup. A typical ANOVA model looks like what follows.
![]() (4)
(4)
where ![]() is the effect of the ith level of the row factor and
is the effect of the ith level of the row factor and ![]() the effect of the jth level of the column factor, respectively. The term
the effect of the jth level of the column factor, respectively. The term ![]() represents the effect of the interaction between
represents the effect of the interaction between ![]() and
and![]() . Normally, this model is subject to the following constraints.
. Normally, this model is subject to the following constraints.
![]() (5)
(5)
Such an ANOVA model can be transformed into a regression model. One way of defining the regression model corresponding to this model is as follows:
![]() (6)
(6)
![]()
This model is also subject to the constraints in Equation (5). This type of modeling is often called “effect modeling” or “incremental effect parameterization”.
2.3. Odds Ratio Assessment
The odds ratio (OR) is defined as the ratio of any odds of experimental subgroup to that of the referent one.
![]() (7)
(7)
In this study, we found that if the odds ratio is less than or equal to one; i.e., ![]() , then the following holds:
, then the following holds:
![]() (8)
(8)
If we are sure that the upper and lower limits of ![]() with
with ![]() confidence, then the upper limit of two-sided
confidence, then the upper limit of two-sided ![]() CI corresponds to that of one-sided
CI corresponds to that of one-sided ![]() confidence interval.
confidence interval.
2.4. Interaction Assessment
As defined in Kleinbaum and Klein [9] , an equation for assessing interaction can be identified as follows. We begin with the null hypothesis that:
![]() (9)
(9)
It is interesting to note that the interaction effects can be expressed to be multiplicative. One way to state this null hypothesis, in terms of odds ratios, is that ![]() equals the product of
equals the product of ![]() and
and![]() .
.
![]() (10)
(10)
If the equation of this null hypothesis is satisfied, we say that there is “no interaction on a multiplicative scale.” In contrast, if this expression does not hold, we say that there is “evidence of interaction on a multiplicative scale.”
We can make use of this formula to test the null hypothesis ![]() of no interaction on a multiplicative scale. If null hypothesis is true, then we can interpret the hypothesis in either way.
of no interaction on a multiplicative scale. If null hypothesis is true, then we can interpret the hypothesis in either way.
![]() (11)
(11)
2.5. Estimation of Regression Parameters
We consider generalized linear models in which the outcome variables are measured on a binary scale, as explained in Dobson and Barnett [11] . For example, the responses may be “success” or “failure” or non-conform- ing or conforming. “S” and “F” denoted by 1 or 0 are used as generic terms of the two categories. First, the binary random variable is defined.
![]() (12)
(12)
with probabilities ![]() and
and![]() , which is the Bernoulli distribution. Suppose there are
, which is the Bernoulli distribution. Suppose there are ![]() such random variables
such random variables ![]() which are independent of each other with
which are independent of each other with![]() . In the case where the
. In the case where the![]() ’s are all equal, we can define a new random variable
’s are all equal, we can define a new random variable ![]() so that
so that ![]() is the number of successes in
is the number of successes in ![]() trials. The random variable
trials. The random variable ![]() has the binomial distribution:
has the binomial distribution:
![]() (13)
(13)
In Dobson and Barnett [11] , the one factor case of ![]() independent random variables
independent random variables ![]() corresponding to the number of successes in
corresponding to the number of successes in ![]() different subgroups. If
different subgroups. If![]() , the log-likelihood function is
, the log-likelihood function is
![]() (14)
(14)
In this study, we intend to extend this one-way single factor case to two-way two factor case.
We consider the case of ![]() independent random variables
independent random variables ![]() corresponding to the numbers of successes in
corresponding to the numbers of successes in ![]() two-way subgroups as in Table 1.
two-way subgroups as in Table 1.
If we define![]() , then the likelihood function can be given by:
, then the likelihood function can be given by:
![]() (15)
(15)
Since![]() , the log-likelihood function becomes:
, the log-likelihood function becomes:
![]() (16)
(16)
![]()
Table 1. Frequencies of ![]() binomial distributions.
binomial distributions.
As defined in Equation (7),![]() . It follows that
. It follows that ![]() and
and![]() . The log likelihood function takes the form of:
. The log likelihood function takes the form of:
![]() (17)
(17)
The partial derivative and the Hessian of this likelihood function with respect to ![]() give the score vector and the information matrix
give the score vector and the information matrix![]() , respectively. As explained in Montgomery et al. [8] , numerical search methods could be used to compute the maximum likelihood estimate (MLE)
, respectively. As explained in Montgomery et al. [8] , numerical search methods could be used to compute the maximum likelihood estimate (MLE) ![]() for
for![]() . Alternatively, one can use iteratively reweighted least squares (IRLS) to actually find the MLEs. The MLE
. Alternatively, one can use iteratively reweighted least squares (IRLS) to actually find the MLEs. The MLE ![]() for
for ![]() can be obtained by the following recursive equation.
can be obtained by the following recursive equation.
![]() (18)
(18)
This is usually called generalized estimating equation (GEE). For more details, refer to Montgomery et al. [8]
and Dobson and Barnett [11] . The information matrix corresponds to![]() . The inverse of information
. The inverse of information
matrix ![]() is the estimated variance-covariance matrix for
is the estimated variance-covariance matrix for![]() . If we let
. If we let ![]() be the final estimate vector, then
be the final estimate vector, then
![]() (19)
(19)
where the ![]() is an
is an ![]() diagonal matrix containing the estimated variance on the main diagonal; that is, the ith diagonal element of
diagonal matrix containing the estimated variance on the main diagonal; that is, the ith diagonal element of ![]() is
is![]() . If the model is a good fit of the data, the deviance
. If the model is a good fit of the data, the deviance ![]() should approximately have the distribution
should approximately have the distribution![]() , where
, where ![]() is the different values of
is the different values of ![]() and
and ![]() is the number of parameters in the model.
is the number of parameters in the model.
2.6. Interval Estimation of Fractions
The odds can be estimated by ![]() and the odds ratio can be expressed by the antilog of the corresponding parameter. The fitted fraction estimate for the logistic regression model is written by:
and the odds ratio can be expressed by the antilog of the corresponding parameter. The fitted fraction estimate for the logistic regression model is written by:
![]() (20)
(20)
This is the point estimate for the fraction of each subgroup of outcomes. To obtain the interval estimation, prediction vectors are needed. Let ![]() be the fraction to be estimated and
be the fraction to be estimated and ![]() be a row vector of prediction.
be a row vector of prediction.
![]() (21)
(21)
The expectation and variance can be given by:
![]() (22)
(22)
The ![]() lower and upper limit of
lower and upper limit of ![]() at
at ![]() can be calculated as follows:
can be calculated as follows:
![]() (23)
(23)
By taking the reciprocals, ![]() confidence interval for
confidence interval for ![]() can be calculated by:
can be calculated by:
![]() (24)
(24)
In the estimation process, the precision varies depending on the sample size of each subgroup. The bigger the sample size is, the more accurate the fraction estimates are.
There exist excellent computer programs that implement maximum-likelihood estimation for logistic regression, such as SAS PROC LOGISTIC in Allison [14] and MINITAB [15] . We have only to apply ourselves to modeling and parameterization.
3. Illustrative Example of Qualitative Predictors
3.1. Illustrative Example
A manufacturing company produces touch-screen panels on a massive scale to deliver to a customer company, who produces smart phones and tablet PCs. Currently, resistive touch-screen panels (TSP) are being widely used. The company plans to produce capacitive TSP (CTSP) to minimize the thickness. However, the following problems may be caused during the fabrication of CTSP. For example, after performing the screen printing process, when an Ag paste is cured at a high temperature, cracks may occur in a fine indium tin oxide (ITO) line. Moreover, many defects such as air bubbles, alien substances and scratches, may take places during the interlayer lamination process. The defective items are the major source of failure cost of the product.
An experimenter is seeking a method of fabricating the CTSP that can efficiently reduce the cost of CTSP fabrication, which can be assessed in terms of yield rate or fraction non-conforming. There are four patented methods of fabrication and four types of facilities available for the process operation. The experimenter is concerned with handling with explanatory variables that are qualitative and contain three or more levels.
3.2. Units of Nonconforming
Since the example lends itself to the problem of two-way binary data, let us consider two qualitative factor experiments with ![]() levels of factor
levels of factor ![]() (facility),
(facility), ![]() levels of factor
levels of factor ![]() (manufacturing method), and
(manufacturing method), and ![]() replicates except the current manufacturing condition with
replicates except the current manufacturing condition with ![]() replicates. The units of product data either conforming or nonconforming are given in Table 2. The data are grouped as frequencies for each combination of factor levels. There are sixteen cells within the table, each of which corresponds to a certain manufacturing condition. A fixed effect model seems to be appropriate for the data, since the levels of factors are not randomly chosen.
replicates. The units of product data either conforming or nonconforming are given in Table 2. The data are grouped as frequencies for each combination of factor levels. There are sixteen cells within the table, each of which corresponds to a certain manufacturing condition. A fixed effect model seems to be appropriate for the data, since the levels of factors are not randomly chosen.
Expressed in terms of the combination of factor levels, the subgroup ![]() is the referent cell representing current manufacturing condition. The referent cell, also called the control subgroup
is the referent cell representing current manufacturing condition. The referent cell, also called the control subgroup ![]() of this experiment, consists of the individual Bernoulli trials. The trials belonging to the cells other than the referent cell are members of the corresponding experiment subgroup or experiment cell. Let
of this experiment, consists of the individual Bernoulli trials. The trials belonging to the cells other than the referent cell are members of the corresponding experiment subgroup or experiment cell. Let ![]() denote the fraction of each subgroup where units of product will not conform to specification. The quantity
denote the fraction of each subgroup where units of product will not conform to specification. The quantity ![]() is so called yield rate of each process corresponding to the combination of factor levels.
is so called yield rate of each process corresponding to the combination of factor levels.
The experimenter is concerned about the optimal subgroup and the significance of the fractions of these experimental subgroups, eventually to find out the improved experimental subgroup, if any, which gives the lowest ![]() in the statistical sense.
in the statistical sense.
3.3. ANOVA with Logistic Transformation
The logistically transformed log-odds data shown in Table 3 can be regarded as a two-way layout without
![]()
Table 2. Units of product nonconforming.
![]()
Table 3. Logistically transformed data.
replications.
The following model seems to be relevant as far as the ANOVA is concerned.
![]() (25)
(25)
Since this is a two-way layout without replication, the interactions are not considered in the model. Based on the model, the ANOVA can be conducted as in Table 4.
Factor ![]() looks significant at 95% significance level, factor
looks significant at 95% significance level, factor ![]() does not. The smaller the nonconforming fraction is, the better its performance is. The minimum point estimate for nonconforming fraction can be calculated by:
does not. The smaller the nonconforming fraction is, the better its performance is. The minimum point estimate for nonconforming fraction can be calculated by:
![]() (26)
(26)
Since the number of effective replication is given by:
![]() (27)
(27)
The 95% confidence interval for ![]() can be calculated as:
can be calculated as:
![]() (28)
(28)
The result of Minitab processing can be obtained as in Figure 2.
The point estimate for ![]() can be given by:
can be given by:
![]() (30)
(30)
Likewise, the 95% confidence interval for ![]() can be calculated as:
can be calculated as:
![]() (30)
(30)
The result is quite plausible in that the interval is narrower than before and the lower limit can never be a negative. However, the optimal manufacturing condition of ANOVA is![]() , not
, not![]() . Moreover, we have some misgivings about the fact that since the sample size is ignored. Some of the sample information must be lost during the course of the analyzing process. For this reason, we are encouraged to give a try to logistic regression.
. Moreover, we have some misgivings about the fact that since the sample size is ignored. Some of the sample information must be lost during the course of the analyzing process. For this reason, we are encouraged to give a try to logistic regression.
3.4. Logistic Regression for the Illustrative Example
The data structure for the illustrative example shown in Table 2 is identified as follows:
![]() (31)
(31)
where ![]() and
and ![]() denotes the main effects of factor
denotes the main effects of factor ![]() and
and![]() , respectively. As a preliminary model,
, respectively. As a preliminary model, ![]() is needed to represent potential interaction effect. In a logistic regression, if we adopt the logit link function, then the model for the data in Table 2 can be stated as in the following equation. This is an extension of one predictor model in Agresti [10] and a leverage of two predictor model in Strokes et al. [13] . This is what we call ANOVA-model like parameterization of logistic regression.
is needed to represent potential interaction effect. In a logistic regression, if we adopt the logit link function, then the model for the data in Table 2 can be stated as in the following equation. This is an extension of one predictor model in Agresti [10] and a leverage of two predictor model in Strokes et al. [13] . This is what we call ANOVA-model like parameterization of logistic regression.
![]() (32)
(32)
where ![]() is the column vector of model parameters and
is the column vector of model parameters and ![]() is the row vector of corresponding indicator values. This model is also subject to the following constraints.
is the row vector of corresponding indicator values. This model is also subject to the following constraints.
![]() (33)
(33)
There are several ways of handling these constraints as in Dobson and Barnett [11] . One of those methods is to set to zero the first term of each constraint. That is,
![]() (34)
(34)
If ![]() in the model is so determined, then
in the model is so determined, then ![]() in represents the mean of the referent subgroup
in represents the mean of the referent subgroup![]() . The parameters
. The parameters![]() ,
, ![]() and
and ![]() are the incremental main effects for method 2, 3 and 4, respectively as compared to referent subgroup. Likewise,
are the incremental main effects for method 2, 3 and 4, respectively as compared to referent subgroup. Likewise, ![]() and
and ![]() are the incremental main effects for facility 2 and 3, respectively. The interactions are also incremental. Expressed in terms of matrix and vector notation, the incremental effect parametric logistic regression model is analogous to the conventional model of
are the incremental main effects for facility 2 and 3, respectively. The interactions are also incremental. Expressed in terms of matrix and vector notation, the incremental effect parametric logistic regression model is analogous to the conventional model of![]() .
.
Let ![]() denote the row vector of the design matrix
denote the row vector of the design matrix ![]() corresponding to the combination of factor levels
corresponding to the combination of factor levels![]() . The sample logit vector
. The sample logit vector![]() , the design matrix
, the design matrix![]() , and the parameter vector
, and the parameter vector ![]() are as follows.
are as follows.
![]() (35)
(35)
The explanatory variables are all indicators. Notice that the columns corresponding to![]() ,
, ![]() ,
, ![]() ,
, ![]() and
and ![]() are eliminated to avoid the redundancy of column vectors. Some columns of the matrix are orthogonal to each other and some columns are interrelated. It is interesting to note that the design matrix enjoys a special structure. The adoption of some parameters is a matter of choice. For instance, we can eliminate
are eliminated to avoid the redundancy of column vectors. Some columns of the matrix are orthogonal to each other and some columns are interrelated. It is interesting to note that the design matrix enjoys a special structure. The adoption of some parameters is a matter of choice. For instance, we can eliminate![]() ,
, ![]() and
and ![]() columns and the corresponding rows
columns and the corresponding rows![]() ,
, ![]() and
and ![]() from the design matrix
from the design matrix ![]() simultaneously without affecting the estimates of the rest of the parameters.
simultaneously without affecting the estimates of the rest of the parameters.
3.5. Estimation of Parameters
The full pattern of model 1 is fitted into the data in Table 2. Minitab logistic regression output is displayed in Figure 3.
*: significant at 5% **: significant at 1%
Figure 2. 95% confidence and prediction interval (Minitab).
![]()
Figure 3. Parameter estimates for model 1.
Figure 3. Parameter estimates for model 1.
The p-values and the CI’s of odds ratios can be regarded as measures of the significance tests of regression parameters. Some parameters look significant, but others do not. As a matter of fact, regardless of whether parameters are significant or not, we can eliminate any rows or columns from the table on purpose without affecting the estimation of other parameters, owing to the incremental effect parameterization.
For example, we are interested in comparison of reference subgroup and strong candidate subgroup for optimality. Since the combination ![]() is the strong candidate for optimality, we can eliminate row 2 and 4 and also columns 3 from Table 2. By doing so, we can drastically reduce the data table until it becomes as small as
is the strong candidate for optimality, we can eliminate row 2 and 4 and also columns 3 from Table 2. By doing so, we can drastically reduce the data table until it becomes as small as![]() ,
, ![]() or
or![]() . If we had known the fact, we could have started with the data table of size
. If we had known the fact, we could have started with the data table of size![]() ,
, ![]() or
or![]() . In this case, the resultant table is
. In this case, the resultant table is ![]() as shown in Table 5. Note that the table includes both referent and candidate subgroups.
as shown in Table 5. Note that the table includes both referent and candidate subgroups.
Likewise, the logistic regression model reduces to the following.
![]() (36)
(36)
The design matrix ![]() and the parameter vector
and the parameter vector ![]() are identified as follows.
are identified as follows.
![]() , (37)
, (37)
The parameter estimates are shown in Figure 4. It is worthy to note that the parameter estimates remain the same. We can ensure that the elimination of rows and columns does not affect the parameter estimates. The phenomenon that makes matters simple is the major difference between ANOVA-type and incremental effect modeling.
On the one hand, ![]() seems insignificant because the corresponding p-value 0.234 is greater than 0.10 and the 90% confidence interval for odds ratio (0.83, 3.31) contains one. On the other hand,
seems insignificant because the corresponding p-value 0.234 is greater than 0.10 and the 90% confidence interval for odds ratio (0.83, 3.31) contains one. On the other hand, ![]() is affirmatively significant in that the upper and lower limits of 90% CI are smaller than one. We decide to eliminate the
is affirmatively significant in that the upper and lower limits of 90% CI are smaller than one. We decide to eliminate the ![]() column and the corresponding row from the design matrix for the parsimony of the model. The model becomes
column and the corresponding row from the design matrix for the parsimony of the model. The model becomes
![]() (38)
(38)
The design matrix ![]() and the parameter vector
and the parameter vector ![]() are reduced and identified as follows:
are reduced and identified as follows:
![]() , (39)
, (39)
The parameter estimates are shown in Figure 5.
The estimate for ![]() changes, but still
changes, but still ![]() does not. The estimates for
does not. The estimates for ![]() and
and ![]() seem to be significant at 10%. Note that the equation of model 3 could be the final one, because all parameter estimates are significant at 10%. We can draw a conclusion that the model is appropriate.
seem to be significant at 10%. Note that the equation of model 3 could be the final one, because all parameter estimates are significant at 10%. We can draw a conclusion that the model is appropriate.
3.6. Existence of Interactions
Notice that the estimate for the interaction ![]() is significant at 10%. The last line of Figure 5 gives the information on the point estimate and CI for
is significant at 10%. The last line of Figure 5 gives the information on the point estimate and CI for![]() . The estimate for
. The estimate for ![]() is 0.28, which is the quantity of
is 0.28, which is the quantity of![]() . The 90% CI for
. The 90% CI for ![]() is (0.09, 0.84) as in Figure 5, the upper and lower limits of which are smaller than 1 and hence affirmatively significant. Therefore, it is the evidence that there exists interaction. In this case,
is (0.09, 0.84) as in Figure 5, the upper and lower limits of which are smaller than 1 and hence affirmatively significant. Therefore, it is the evidence that there exists interaction. In this case, ![]() , thus we can make sure that
, thus we can make sure that
![]() (40)
(40)
Usually, equality does not hold, unless![]() . In other words, there is the evidence that interaction exists if and only if
. In other words, there is the evidence that interaction exists if and only if ![]() or the antilog of
or the antilog of ![]() is other than 1. If the interaction does not exist, then
is other than 1. If the interaction does not exist, then
![]() (41)
(41)
3.7. Estimation of Confidence Intervals
We can ensure that the point estimates for each fraction can be obtained as follows:
![]() table_table_table
table_table_table
Figure 4. Parameter estimates for model 2.
![]()
Figure 5. Parameter estimates for model 3.
Figure 5. Parameter estimates for model 3.
![]()
![]()
From a conventional statistical view point, we might like to calculate the confidence intervals. To find confidence intervals, we have to know the standard errors ![]() of the model parameter estimates. The parameter estimates reported in Figure 5 are just the square roots of the main diagonal elements of the variance-covariance
of the model parameter estimates. The parameter estimates reported in Figure 5 are just the square roots of the main diagonal elements of the variance-covariance
matrix![]() . The confidence interval for
. The confidence interval for ![]() can be calculated as follows:
can be calculated as follows:
90% CI for![]() :
: ![]()
90% CI for![]() :
: ![]()
In the same way, we can calculate the confidence intervals for ![]() and
and![]() . By the way, we need to know the information on the variance-covariance of parameter estimates, which can be obtained in the form of variance-covariance matrix. But the calculations are not that simple due to the fact that
. By the way, we need to know the information on the variance-covariance of parameter estimates, which can be obtained in the form of variance-covariance matrix. But the calculations are not that simple due to the fact that
![]() (42)
(42)
![]() (43)
(43)
In general, the standard errors corresponding to![]() ,
, ![]() and
and ![]() can be calculated by
can be calculated by
![]() (44)
(44)
where ![]() is a row vector of
is a row vector of ![]() corresponding to
corresponding to![]() ,
, ![]() or
or![]() . There exists commercialized program such as SAS PROC LOGISTIC and/or MINITAB, which performs those cumbersome calculations for us. Once we have those computer programs at our finger tips and the knack of modeling, it is no big deal to calculate the confidence intervals. The point and interval estimates for fractions can be reported as in Table 6, which is a translation of MINITAB output.
. There exists commercialized program such as SAS PROC LOGISTIC and/or MINITAB, which performs those cumbersome calculations for us. Once we have those computer programs at our finger tips and the knack of modeling, it is no big deal to calculate the confidence intervals. The point and interval estimates for fractions can be reported as in Table 6, which is a translation of MINITAB output.
The confidence intervals can provide us with the information on whether the sample size is large enough or not. For example, the interval estimates for ![]() and
and ![]() in Table 6 overlap considerably and hence the interval estimates are not discriminative, seemingly because of the fact that the number of replication of subgroup
in Table 6 overlap considerably and hence the interval estimates are not discriminative, seemingly because of the fact that the number of replication of subgroup ![]() is not large enough. But we have to bear in mind that this is the conventional way of interpreting the result. We do not have to see the problem in this manner.
is not large enough. But we have to bear in mind that this is the conventional way of interpreting the result. We do not have to see the problem in this manner.
![]()
Table 6. Point and interval estimates for fractions of model 3.
3.8. Collection of More Data
Sometimes we might have to see the problem in another way. In order to make the two subgroups ![]() and
and ![]() contrasting, we construct a
contrasting, we construct a ![]() data table as in Table 7.
data table as in Table 7.
The logistic regression model becomes as simple as the following.
![]() (45)
(45)
The parameter ![]() is adopted as a combination of
is adopted as a combination of ![]() and
and![]() .The following is the corresponding design matrix and parameter vector.
.The following is the corresponding design matrix and parameter vector.
![]() , (46)
, (46)
The parameter estimates are shown in Figure 6.
The interval estimate (0.21, 1.63) for ![]() contains 1, which means
contains 1, which means ![]() is insignificant. We need more replications especially with the
is insignificant. We need more replications especially with the ![]() subgroup. There exist related sample size formulae for comparing proportions in order to calculate the required sample size for a simple logistic regression model in Hsieh et al. [16] .
subgroup. There exist related sample size formulae for comparing proportions in order to calculate the required sample size for a simple logistic regression model in Hsieh et al. [16] .
A simulated data are given in Table 8 where the numbers of replications are increased up to 1000 with the referent subgroup ![]() and up to 500 with the experimental subgroup
and up to 500 with the experimental subgroup![]() , while the fractions remain the same.
, while the fractions remain the same.
Model 4 is fitted into the data. The design matrix ![]() and the parameter vector
and the parameter vector ![]() are the same with model 4. The parameter estimates are shown in Figure 7.
are the same with model 4. The parameter estimates are shown in Figure 7.
The estimate ![]() is significant at 10% and both the lower and upper limits are smaller than 1. We can say with 95% confidence that
is significant at 10% and both the lower and upper limits are smaller than 1. We can say with 95% confidence that ![]() as explained before. Seen from the last line of Figure 7, we can ascertain that the odds ratio is less than one, since we know that if
as explained before. Seen from the last line of Figure 7, we can ascertain that the odds ratio is less than one, since we know that if![]() , then
, then
![]() (47)
(47)
If we are sure that the upper and lower limits of ![]() is smaller than one with 90% confidence, then we can say that the upper limit of two-sided 90% confidence interval corresponds to that of one-sided 95% confidence interval.
is smaller than one with 90% confidence, then we can say that the upper limit of two-sided 90% confidence interval corresponds to that of one-sided 95% confidence interval.
Seen from the conventional view point of statistics, the point and interval estimates for fractions can be given as in Table 9. Since the confidence intervals overlap, the intervals are not discriminative enough.
In this manner, an experimenter can decide on whether parameter estimates are significant, whether the model is appropriate, whether sample size is large enough, and whether the fraction of candidate subgroup is smaller, until he or she is convinced that the candidate subgroup is superior to the current one.
4. Conclusion and Further Study
In reality, there are many cases where an experimenter has to analyze fraction data, usually provided in the form of percentages or yield rates as the outcomes of an experiment. The input variables are quantitative, qualitative, or both. In this study, the case that the two input variables are all qualitative and the responses are countable is considered for study in order to extend the model in Agresti [10] and leverage the logistic model in Strokes et al. [13] . That is to say, an attempt is given to the problem of binary outcomes with two categorical predictors by
![]()
![]()
Table 9. Point and interval estimates for fractions of model 3.
Figure 6. Parameter estimates for model 4.
![]()
Figure 7. Parameter estimates for model 4.
Figure 7. Parameter estimates for model 4.
utilizing logistic regression. In this study, we excluded ANOVA-type analyses, but we adopted ANOVA-model like parameterization, that is, incremental effect modeling.
The optimal manufacturing condition can be ensured, mainly by testing the significance of regression parameters, testing the existence of interactions, estimating related confidence intervals, testing the difference of mean values, and so on. The conventional ANOVA-type analyses are based on the assumption of normality, independence, and equality of variances of experimental observations. For this reason, the ANOVA-type model entails much detrimental to the goodness-of-fit test and the efficient and precise estimation of regression parameters, mainly because the additive property of fraction data is no longer valid, especially when the fractions are close to zero or is near one, as discussed by Jaeger [6] .
As it is always the case with logistic regression, the point estimates are more accurate than those of ANOVA- type modeling. Not only is the lower limit always positive, but also the upper limit is always less than one. The significance test of a parameter can be performed by checking whether the confidence interval of the corresponding odds ratio contains one or not, based on the assumption that the null hypothesis ![]() is true. The interpretation from the viewpoint of logistic regression is not only different from, but also superior to that of ANOVA-type analysis in the statistical sense, as far as the fraction data are concerned. We have to see the model and interpret the result as it is. The model may not be seen from conventional statistical view point.
is true. The interpretation from the viewpoint of logistic regression is not only different from, but also superior to that of ANOVA-type analysis in the statistical sense, as far as the fraction data are concerned. We have to see the model and interpret the result as it is. The model may not be seen from conventional statistical view point.
When dealing with logistic regression with categorical predictors, the generalized estimating equations (GEE) must be utilized to estimate the parameters. These demerits, nevertheless, can be easily overcome by making use of commercialized computer programs such as SAS PROC LOGISTIC and MINITAB. The analyzing process is somewhat different from the conventional statistical analysis method. We might have to abandon our conventional ANOVA-type of way to interpret the analysis result.
The use of logistic regression has its merits: 1) the analyzer can never get a yield rate or defective rate estimate either above 1 or below 0, 2) the estimates for parameters are more efficient and accurate compared to those of the ANOVA-type model since the logistic regression model describes more accurately the intrinsic nature of the count data, and 3) the significance test of regression parameters is easily performed by checking the interval estimates for odds ratios.
There exist other types of transformations, not mentioned in this study, such as probit and complementary log-log transformations, which seems to be worthy of trying. The logistic regression model is sometimes called ordinary logit model to distinguish it from what they call mixed logit model. The mixed logit model could be the next topic of this study.
The analyses method discussed throughout this study can be extended to the case of multiple qualitative predictors for count data, just as there are a variety of models available in the literature, especially in the area of experimental design and regression analysis.
Acknowledgements
This research was supported by Seokyeong University in 2013.
NOTES
*Effect modeling means “incremental effect parameterization”.