The Application and Adaptation of the Two Sources of Code and Natural Encoding Method for Designing a Model of Microprogram Control Unit with Base Structure ()
1. Introduction
Control units are very important parts of digital systems [1] -[6] . Nowadays, complex programmable logic devices (CPLD) are widely used for implementing logic circuits of control units [7] [8] . However, the issue of reducing the size of a control unit is still a subject of current interest. Finding a solution to this issue will make it possible to improve such indicators as the speed of performance and the power consumption of the designed system [9] [10] . CPLDs include macrocells of programmable array logic (PAL) with a limited number of terms. To reduce the amount of hardware in the logic circuit of a control unit, the peculiarities of the CPLD and the features of a control algorithm to be implemented should be taken into account. If a control algorithm is represented by a linear graph-scheme of the algorithm (GSA), then a model of the compositional microprogram control unit (CMCU) can be used for its interpretation [11] . It is assumed by the authors that the control memory (CM) of the CMCU can be implemented as external PROM/ROM memory. Some of the CPLD family devices are equipped with integrated memory. For example, Altera CPLD devices are equipped with user flesh memory (UFM) [12] , whereas Cypress CPLD devices are equipped with cluster memory blocks (CMB) [13] . This article presents a mathematical model and a design algorithm with two sources of code and natural encoding which has been modified and adopted to CMCU model with base structure [14] [15] .
2. Background of the CMCU with Base Structure and Two Sources of Code
It is assumed that the GSA is represented by sets of vertices 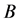 where
where 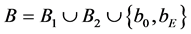 and a set of arcs
and a set of arcs  where
where . It is further assumed that
. It is further assumed that 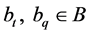 and
and 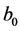 is an initial vertex,
is an initial vertex, 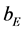 is a final vertex,
is a final vertex,  is a set of operator vertices,
is a set of operator vertices, 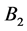 is a set of conditional vertices. A vertex contains a microinstruction
is a set of conditional vertices. A vertex contains a microinstruction 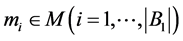 and
and  is a set of data-path microoperations
is a set of data-path microoperations 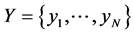 [16] - [18] . Each vertex
[16] - [18] . Each vertex 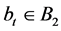 contains a single element
contains a single element  of a set of logical conditions
of a set of logical conditions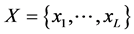 . A set
. A set of operational linear chains (OLC) for the GSA shall be formed, where each OLC is a sequence of operator vertices and each pair of its adjacent components corresponds to an arc of the GSA.
of operational linear chains (OLC) for the GSA shall be formed, where each OLC is a sequence of operator vertices and each pair of its adjacent components corresponds to an arc of the GSA.
![]() . (1)
. (1)
Each OLC ![]() has only one output
has only one output ![]() and an arbitrary number of inputs
and an arbitrary number of inputs![]() . The
. The ![]() elements are under- stood as a state of the system which is identified by
elements are under- stood as a state of the system which is identified by ![]() elements. OLC outputs make up the collection
elements. OLC outputs make up the collection![]() . Formal definitions of OLC, its input and output can be found in [11] . Each vertex from
. Formal definitions of OLC, its input and output can be found in [11] . Each vertex from ![]() corresponds to microinstruction
corresponds to microinstruction ![]() stored in the control memory (CM) of CMCU and it has an address
stored in the control memory (CM) of CMCU and it has an address![]() . The microinstructions can be addressed using
. The microinstructions can be addressed using ![]() bits, where
bits, where
![]() (2)
(2)
and the bits are represented by variables from the set![]() :
:
![]() . (3)
. (3)
Assuming that the ![]() OLC includes
OLC includes ![]() components, the following condition takes place:
components, the following condition takes place:
![]() . (4)
. (4)
In Equation (4) ![]() is the i-th component of OLC. The first source of information about the state of the system is the register RG. The Value of used filp-flops needed for the implementation RG is
is the i-th component of OLC. The first source of information about the state of the system is the register RG. The Value of used filp-flops needed for the implementation RG is![]() , where:
, where:
![]() . (5)
. (5)
The flip-flops outputs are represented by variables from the set![]() :
:
![]() . (6)
. (6)
The second source of information about the state of the system is the unused space of the control memory (CM) [19] [20] . An external PROM chip or memory integrated with the CPLD may be applied to implement the CM. The memory has ![]() outputs, where
outputs, where![]() , 4, 8, 16 [21] . Some information can be implemented using free outputs of the CM. it is assumed that one-hot encoding of microoperations is used [22] - [26] . The CM word has
, 4, 8, 16 [21] . Some information can be implemented using free outputs of the CM. it is assumed that one-hot encoding of microoperations is used [22] - [26] . The CM word has ![]() bits, where
bits, where
![]() . (7)
. (7)
Thus, the number of available unused flip-flops is:
![]() . (8)
. (8)
The ![]() bits are represented by variables from the set
bits are represented by variables from the set![]() :
:
![]() . (9)
. (9)
If the condition
![]() (10)
(10)
takes place, the method can be used. The number of repetitions of each state occurring as the initial state is counted in the transitions of the algorithm. The states of the system are identified through the outputs ![]() of the operational linear chains. The outputs belong to the collection
of the operational linear chains. The outputs belong to the collection![]() . The
. The ![]() most used
most used ![]() items shall be taken. Next, these items shall be moved to a new collection
items shall be taken. Next, these items shall be moved to a new collection![]() . Following the above assumptions, an equation
. Following the above assumptions, an equation
![]() (11)
(11)
takes place. The collection ![]() has been divided into two collections
has been divided into two collections ![]() and
and![]() , where
, where![]() . The control memory CM is a source of the variables
. The control memory CM is a source of the variables ![]() applied to encode
applied to encode ![]() by the code
by the code![]() . The register RG is a source of the variables
. The register RG is a source of the variables ![]() applied to encode
applied to encode ![]() by the code
by the code![]() . Provided that the assumption presented in equation (11) is fulfilled, it is possible to apply the one-hot encoding to the elements from the collection
. Provided that the assumption presented in equation (11) is fulfilled, it is possible to apply the one-hot encoding to the elements from the collection![]() .
.
The combinational circuit (CC) generates data ![]() for the counter (CT) and data
for the counter (CT) and data ![]() for the register (RG):
for the register (RG):
![]() , (12)
, (12)
![]() . (13)
. (13)
The synthesis of the CMCU algorithm includes the following steps:
1) Forming the set of OLCs.
2) Forming the control memory content.
3) Forming the transition table of the CMCU.
4) Counting the occurrence of ![]() on the basis of the transition.
on the basis of the transition.
5) Dividing the collection ![]() into two collections
into two collections ![]() and
and![]() .
.
6) Updating the control memory content.
7) Forming the excitation functions for the CT and RG with using two sources of code.
8) Synthesis of the logic circuit of CMCU.
Figure 1 presents a structural diagram of the CMCU with two sources of code. The pulse Start causes loading of the first microinstruction address into a counter CT and set up of a fetch flip-flop TF. If![]() , then microinstructions can be read out from the control memory CM. If a current microinstruction does not correspond to an OLC output, then a special variable
, then microinstructions can be read out from the control memory CM. If a current microinstruction does not correspond to an OLC output, then a special variable ![]() is formed together with microoperations
is formed together with microoperations![]() . If
. If![]() , then content of the CT is incremented according to the addressing mode. Otherwise, the block of combinational circuit logic (CC) generates functions
, then content of the CT is incremented according to the addressing mode. Otherwise, the block of combinational circuit logic (CC) generates functions ![]() and
and![]() . If
. If![]() , then the CMCU stops and new data from CM is not loaded.
, then the CMCU stops and new data from CM is not loaded.
3. Main Idea behind the Proposed Method
The excitation functions generating data for the counter CT and register RG in Equation (12) and Equation (13)
![]()
Figure 1. Structural diagram of CMCU U1.
are built with the use of logical terms. Let ![]() and
and ![]() be such collections of excitation functions required to realize Equation (12) and Equation (13), that:
be such collections of excitation functions required to realize Equation (12) and Equation (13), that:
![]() , (14)
, (14)
![]() . (15)
. (15)
Functions from the collections ![]() and
and ![]() generate data represented by the variables depicted in Equation (3) and Equation (4). The terms which are used for building the excitation functions are created by joining two parts: the conjunction of conditions
generate data represented by the variables depicted in Equation (3) and Equation (4). The terms which are used for building the excitation functions are created by joining two parts: the conjunction of conditions ![]() and the code
and the code ![]() or
or![]() . The length of the terms has a direct influence on the number of logical gates used in implementing the CMCU model, and the number of the gates used has, in turn, a direct influence on the size of the realized system. For the base method the maximum length of a term built with the use of the information from the collection
. The length of the terms has a direct influence on the number of logical gates used in implementing the CMCU model, and the number of the gates used has, in turn, a direct influence on the size of the realized system. For the base method the maximum length of a term built with the use of the information from the collection ![]() equals:
equals:
![]() . (16)
. (16)
The maximum length of a term built with the use of information from the collection ![]() equals:
equals:
![]() . (17)
. (17)
The second factor which has a direct influence on the size of the designed system is the possibility of minimizing the excitation functions for the counter CT and register RG. As far as the method with two sources of code is concerned, this possibility is degraded under negative conditions, compared to the method with one source of code. For example, having the OLC elements encoded as in Table 1 and the function for the method with one source of code designed in the following way:
![]()
The excitation function ![]() requires 17 logic gates to be implemented. Let us assume that the system CM has
requires 17 logic gates to be implemented. Let us assume that the system CM has ![]() of unused outputs. In the case of the method with two sources of code and one-hot encoding, as in Table 2 the function
of unused outputs. In the case of the method with two sources of code and one-hot encoding, as in Table 2 the function ![]() shall take the form of
shall take the form of ![]() to realize the same task:
to realize the same task:
![]()
For the analyzed example, the excitation function ![]() requires 18 logic gates to be implemented. Provided that the length of the terms has been reduced according to Equation (17), the possibility of minimizing the excitation functions has been degraded. This results from the peculiarity of one-hot encoding. With such encoding, the terms which use elements from the collection
requires 18 logic gates to be implemented. Provided that the length of the terms has been reduced according to Equation (17), the possibility of minimizing the excitation functions has been degraded. This results from the peculiarity of one-hot encoding. With such encoding, the terms which use elements from the collection ![]() do not undergo minimization. Additionally, minimizing two terms which are built on the basis of information from various sources is also impossible, which leads to an increase in the level of degradation of the possibility of minimizing excitation functions. In order to reduce the level of degradation of the possibility of minimization of excitation functions, the mathematical model and design algorithm with natural encoding has been adopted to the CMCU with base structure [14] [15] . First, natural encoding will be used for encoding information about the state from the CM. In such a case we can use
do not undergo minimization. Additionally, minimizing two terms which are built on the basis of information from various sources is also impossible, which leads to an increase in the level of degradation of the possibility of minimizing excitation functions. In order to reduce the level of degradation of the possibility of minimization of excitation functions, the mathematical model and design algorithm with natural encoding has been adopted to the CMCU with base structure [14] [15] . First, natural encoding will be used for encoding information about the state from the CM. In such a case we can use ![]() information from CM, where
information from CM, where
![]() . (18)
. (18)
In Equation (18), 1 is subtracted to take into account the case when microinstruction is not the source of code. This will be marked by code zero. This code will be not used in excitation functions. To encoding ![]()
![]()
Table 1. OLC items with base structure.
![]()
Table 2. OLC items with two sources of code and one-hot encoding.
elements is used natural encoding. In order to reduce the maximum length of the terms built on the basis of the collection ![]() the following limitation is introduced:
the following limitation is introduced:
![]() . (19)
. (19)
In such a case, the maximum length of a term built with the use of information from the collection ![]() equals:
equals:
![]() . (20)
. (20)
In the analyzed example for the method with two sources of code and natural encoding, as in Table 3, the function ![]() shall become
shall become ![]() in order to realize the same task:
in order to realize the same task:
![]()
The excitation function ![]() requires 11 logic gates to be implemented. Applying natural encoding has made it possible to reduce the level of degradation of the possibility of minimizing of excitation functions. Natural encoding applied to the elements from collection
requires 11 logic gates to be implemented. Applying natural encoding has made it possible to reduce the level of degradation of the possibility of minimizing of excitation functions. Natural encoding applied to the elements from collection ![]() makes it possible to minimize the terms built on the
makes it possible to minimize the terms built on the
![]()
Table 3. OLC items two sources of code and natural encoding.
![]()
Figure 2. Reduction in the size of the system due to the participation of the source.
![]()
Figure 3. Reduction in the size of the system by free bits of memory.
basis of data from this collection. Furthermore, using natural encoding enables transferring a greater amount of information to the collection (source)![]() . Fulfilling the criteria of Equation (19) ensures reduction in the maximum length of the terms, in accordance with Equation (20).
. Fulfilling the criteria of Equation (19) ensures reduction in the maximum length of the terms, in accordance with Equation (20).
4. Results and Conclusions
Figure 2 and Figure 3 present the results of the implementation of the model in real hardware. The Altera family MAX II device EPM1270 F256C5 equipped with UFM has been used for tests. The results presented in Figure 2 and Figure 3 have been obtained from research conducted on 200 randomly generated CMCU models with the following properties:![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() . Red points presented in Figure 2 and Figure 3 show the results obtained with the use of the natural method, whereas the blue points refer to the results obtained with the one-hot method. Figure 2 depicts the relationship between the obtained reduction in the size of the system (in percentage) and the participation of the source of data
. Red points presented in Figure 2 and Figure 3 show the results obtained with the use of the natural method, whereas the blue points refer to the results obtained with the one-hot method. Figure 2 depicts the relationship between the obtained reduction in the size of the system (in percentage) and the participation of the source of data ![]() in generating the excitation functions (in percentage). The application of natural encoding made it possible to avoid the effect of degradation of the possibility of minimizing the functions. A linear interrelation between the participation of the source
in generating the excitation functions (in percentage). The application of natural encoding made it possible to avoid the effect of degradation of the possibility of minimizing the functions. A linear interrelation between the participation of the source ![]() and the obtained reduction in the size of the system has been observed. In the analyzed models with a small participation of the source
and the obtained reduction in the size of the system has been observed. In the analyzed models with a small participation of the source![]() ―within the scope of up to 17%, deterioration of the possibility of minimizing the functions has been observed, which results in an increase in the size required for the realization of the designed system.
―within the scope of up to 17%, deterioration of the possibility of minimizing the functions has been observed, which results in an increase in the size required for the realization of the designed system.
Figure 3 presents the relationship between the obtained reduction in the size of the system (in percentage) and the value of free bits used to representation information from the source![]() . As can be seen in Figure 3, in the case of both the methods there occurs degradation of the possibility of minimizing the functions under negative conditions. The results of conducted experiments indicate that the ability to minimize logic terms and the ability to reduce the length of the terms, which follows from Equation (19) and is characteristic of the natural method, makes it possible to obtain better effects of reducing the system than the ability to reduce the length of logic terms following from Equation (17), yet without the possibility of minimizing the terms from the source
. As can be seen in Figure 3, in the case of both the methods there occurs degradation of the possibility of minimizing the functions under negative conditions. The results of conducted experiments indicate that the ability to minimize logic terms and the ability to reduce the length of the terms, which follows from Equation (19) and is characteristic of the natural method, makes it possible to obtain better effects of reducing the system than the ability to reduce the length of logic terms following from Equation (17), yet without the possibility of minimizing the terms from the source ![]() in the case of the one-hot method. The application of natural encoding improves the level of reduction of the system, compared to the one-hot method. The main factor which enables this improvement is the possibility of minimizing such encoded terms and the representation of a larger amount of data by means of the source
in the case of the one-hot method. The application of natural encoding improves the level of reduction of the system, compared to the one-hot method. The main factor which enables this improvement is the possibility of minimizing such encoded terms and the representation of a larger amount of data by means of the source![]() , using the same free CM resources as in the case of the one-hot method.
, using the same free CM resources as in the case of the one-hot method.
Information
Mr. Łukasz Smoliński is a scholar within Sub-measure 8.2.2 Regional Innovation Strategies, Measure 8.2 Transfer of knowledge, Priority VIII Regional human resources for the economy Human Capital Operational Programme co-financed by European Social Fund and state budget.
![]()
NOTES
*Corresponding author.