Probabilistic Model for Wind Speed Variability Encountered by a Vessel ()
1. Introduction
In the literature typically cumulative distribution function (CDF) of wind speed W, say, is understood as the long-term CDF of the wind speeds at some location or region. The distribution can be interpreted as variability of W at a randomly taken time during a year. Weibull distribution gives often a good fit. Limiting time span to, for example, January month affects the W CDF simply because, as it is the case for many geophysical quantities, the variability of W depends on seasons. To avoid ambiguity when discussing the distribution of W, time span and region over which the observations of W are gathered need to be clearly specified. By shrinking the time span to a single moment t and geographical region to a location p, one obtains (in the limit) the distribution of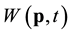 . This is used as the distribution of W in this paper. Obviously the long-term CDF can be retrieved from the “local”
. This is used as the distribution of W in this paper. Obviously the long-term CDF can be retrieved from the “local” 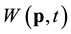 distributions by means of an average of the local distributions, viz for a fixed location p
distributions by means of an average of the local distributions, viz for a fixed location p
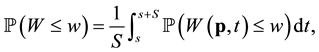 (1)
(1)
where S can be a month, a season or a year. Similarly the long-term CDF over a region A, say, is proportional to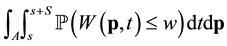 .
.
In order to identify the distributions at all positions p and times t, vast amount of data are needed. Here the reconstruction of W from numerical ocean-atmosphere models based on large-scale meteorological data, called also reanalysis, is utilized to fit a model. The reanalysis does not represent actual measurements of quantities but extrapolations to the grid locations based on simulations from complex dynamical models. It is defined on regular grids in time and space, and hence convenient to use. In this paper, the ERA Interim data [1] produced by European Centre for Medium-Range Weather Forecasts is used to fit the model. However the model can also be fitted to other data sets, e.g. to satellites wind measurements which has also good spatial coverage, see [2] .
Modeling spatial and temporal dependence of wind speed is a very complex problem. Models proposed in the literature are reviewed in [3] . Here we propose to use the transformed Gaussian model, which assumes that there exists a deterministic function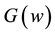 , possibly dependent on location p, such that
, possibly dependent on location p, such that 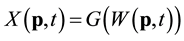 is Gaussian. The
is Gaussian. The 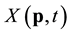 field is defined by the mean
field is defined by the mean 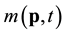 and covariance structure
and covariance structure 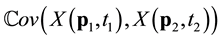 . Obviously for a given transformation G and many years of hind-cast, one could estimate the covariance for any pair
. Obviously for a given transformation G and many years of hind-cast, one could estimate the covariance for any pair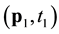 ,
, 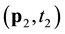 , see, e.g. [4] [5] . However such an approach is limited to relatively small grids in space. Employing the empirical covariances in time and space would result in huge matrices, which limit the applicability of such empirical approach. Consequently, a simple parametric model that catches only some aspects of the wind speed variability, important for a particular application, is of practical interest. The minimal requirements on the model are that it should provide a correct estimates of long-term distributions of the wind speeds, accurate predictions of average durations of the extreme winds conditions and reliable estimates of CDFs of top speeds during storms encountered by a vessel. In order to demonstrate the capability of the proposed model for such minimal requirements, this paper is organized as follows:
, see, e.g. [4] [5] . However such an approach is limited to relatively small grids in space. Employing the empirical covariances in time and space would result in huge matrices, which limit the applicability of such empirical approach. Consequently, a simple parametric model that catches only some aspects of the wind speed variability, important for a particular application, is of practical interest. The minimal requirements on the model are that it should provide a correct estimates of long-term distributions of the wind speeds, accurate predictions of average durations of the extreme winds conditions and reliable estimates of CDFs of top speeds during storms encountered by a vessel. In order to demonstrate the capability of the proposed model for such minimal requirements, this paper is organized as follows:
In Section 2, a general construction of non-stationary model for wind speed variability in time and space is presented. Section 3 presents probabilistic model for the velocity of storms movements. Then statistical properties of some storms characteristics are described in Section 4. The physical interpretations of the introduced parameters are also given in this section and in Appendix 1. In Section 5, on board measured wind speeds are used to validate the proposed model, where the long term CDFs of encountered wind speeds and persistence statistics are used. Total forty routes are used, see Figure 1. The time when routes were sailed are well spread over a year. Finally in Section 6, means to simulate the encountered wind speeds are briefly reviewed. Paper closes with three appendixes containing somewhat more technical matters.
2. Transformed Gaussian Model and Long-Term CDFs
In this section we shall introduce the transformed Gaussian model for the variability of wind speeds. In particular the transformation G making the transformed wind speed data 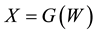 normally distributed will be presented. Seasonal model for the mean and variance of X is given and assumed normality of X validated.
normally distributed will be presented. Seasonal model for the mean and variance of X is given and assumed normality of X validated.
The wind speed 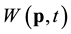 is the ten minutes average of the wind speed measured at position p, defined in degrees of longitude and latitude, while t is the time of the year. We will use the transformation
is the ten minutes average of the wind speed measured at position p, defined in degrees of longitude and latitude, while t is the time of the year. We will use the transformation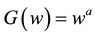 , where a is a fixed constant that depends on the location p, viz
, where a is a fixed constant that depends on the location p, viz
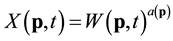 (2)
(2)
The parameter a is nonnegative with convention that the case 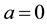 corresponds to the logarithm. We assume that
corresponds to the logarithm. We assume that ![]() is normally distributed.
is normally distributed.
Mean and variance of![]() , denoted by
, denoted by![]() ,
, ![]() , respectively, depend both on position and
, respectively, depend both on position and
![]()
Figure 1. The considered routes in the validation process.
time. The temporal variability of mean and variance is approximated by seasonal components with trends defined as follows
![]() (3)
(3)
![]() (4)
(4)
Here t has units years. This type of model has been used in the literature, see e.g. classical paper [6] .
Remark 1 For a fixed position p, the parameters a and mi in Equation (3) are fitted simultaneously in such a way that the distance between yearly long-term empirical CDF of ![]() and a Gaussian distribution is minimized.
and a Gaussian distribution is minimized.
More precisely for a wind data at fixed position p and parameter ![]() we evaluate
we evaluate ![]() and fit regression Equation (3). Then the residual
and fit regression Equation (3). Then the residual ![]() is evaluated and its empirical CDF estimated. Next a distance between the empirical CDF and the Gaussian CDF (fitted to
is evaluated and its empirical CDF estimated. Next a distance between the empirical CDF and the Gaussian CDF (fitted to![]() ) is evaluated. Finally the parameter a* that minimizes the distance is the estimate of a.
) is evaluated. Finally the parameter a* that minimizes the distance is the estimate of a.
A table of a and mi values as function of the location p is created. As additional parameters of the model will be estimated new columns with parameters estimates will be added to the table. For example, having estimated a and mi the variance![]() , defined in Equation (4), is fitted using an additional assumption that properties of the wind speed changes slowly in time. Then the parameters bi are saved in the table. More details of model estimations are given in Appendix 3.
, defined in Equation (4), is fitted using an additional assumption that properties of the wind speed changes slowly in time. Then the parameters bi are saved in the table. More details of model estimations are given in Appendix 3.
Validation of Gaussianity of ![]()
Ten years of data ![]() were used to estimate parameters a, mi and bi in Equation (3), (4) in North Atlantic on a grid of 0.75 degree. Figure 2 presents the estimates of parameter a. At offshore locations a values vary around 0.8 while close to shore or inlands locations a can be much smaller. Note that small values of a indicate larger departures of the observed wind speeds distribution from the Gaussian one.
were used to estimate parameters a, mi and bi in Equation (3), (4) in North Atlantic on a grid of 0.75 degree. Figure 2 presents the estimates of parameter a. At offshore locations a values vary around 0.8 while close to shore or inlands locations a can be much smaller. Note that small values of a indicate larger departures of the observed wind speeds distribution from the Gaussian one.
Usefulness of the proposed model relies on the accuracy of the approximation of ![]() CDF by Gaussian distribution. The Gaussianity of the process
CDF by Gaussian distribution. The Gaussianity of the process ![]() has been validated for the Northern Atlantic. An example of conducted validations is shown in Figure 3. In the figure the left plot shows ten years of W process limited to two weeks in the middle of February, at locations
has been validated for the Northern Atlantic. An example of conducted validations is shown in Figure 3. In the figure the left plot shows ten years of W process limited to two weeks in the middle of February, at locations![]() ,
, ![]() ,
, ![]() ,
, ![]() , plotted on the normal probability paper. (It is assumed that the winds are stationary for such short period of time.) In the right plot of the figure the transformed data
, plotted on the normal probability paper. (It is assumed that the winds are stationary for such short period of time.) In the right plot of the figure the transformed data ![]() is plotted on normal probability paper. One can see that X CDFs are well approximated by the Gaussian distributions.
is plotted on normal probability paper. One can see that X CDFs are well approximated by the Gaussian distributions.
In the right plots of Figure 4, the standard deviation![]() , defined in Equation (3), is presented for February and August, respectively. One can see that the standard deviation changes considerably with the geographical location but is less dependent on season. We turn next to presentation of variability of the parameter
, defined in Equation (3), is presented for February and August, respectively. One can see that the standard deviation changes considerably with the geographical location but is less dependent on season. We turn next to presentation of variability of the parameter
![]()
Figure 2. Values of parameter a in the transformation Equation (2).
![]()
![]()
Figure 3. Left: Ten years of wind speeds W (t) with t limited to February at the four locations. (−20, 60), (−10, 40), (−40, 50), (−20, 45) plotted on normal probability paper. Right: Transformed wind speeds X (t) limited to February at the four locations plotted on normal probability paper. The values of parameter a in transformation Equation (2) are a = 0.850, 0.675, 0.875, 0.875, respectively.
![]() , i.e. the mean of
, i.e. the mean of ![]() defined in Equation (2). However since units of m are not physical we choo- se to show the variability of the median speed
defined in Equation (2). However since units of m are not physical we choo- se to show the variability of the median speed
![]() (5)
(5)
instead. The values of the median for February and August are presented in two left plots of Figure 4. As expected, wind speeds are higher in winter than in summer.
Finally we check whether the regressions Equations (3) and (4) used to model seasonal variability of m and ![]() leads to accurate estimates of the long-term CDF of W at position p. Employing Gaussianity assumption of X CDF the theoretical long-term CDF of wind speeds at a fixed position p, defined in Equation (1), is given by
leads to accurate estimates of the long-term CDF of W at position p. Employing Gaussianity assumption of X CDF the theoretical long-term CDF of wind speeds at a fixed position p, defined in Equation (1), is given by
![]() (6)
(6)
where ![]() is the CDF of a standard Gaussian (normal) variable. In Figure 5, the yearly probabilities for wind speeds
is the CDF of a standard Gaussian (normal) variable. In Figure 5, the yearly probabilities for wind speeds ![]() computed using Equation (6) at four locations in North Atlantic are compared with the empirical estimates. (The locations are marked by crosses in Figure 2) One can see that the agreement between the estimates is excellent.
computed using Equation (6) at four locations in North Atlantic are compared with the empirical estimates. (The locations are marked by crosses in Figure 2) One can see that the agreement between the estimates is excellent.
![]()
Figure 4. Left top―Median wind speed m [m/s], defined in Equation (5), in February; Left bottom―Median wind speed in August; Right top―Standard deviation of X, computed by means of Equation (4) in February; Right bottom―The standard deviation in August.
![]()
Figure 5. Comparisons of estimates of the long-term probability ![]() for yearly wind speeds variability Equation (1) at four locations defined in degrees of longitude and latitude: (−20, 60), (−10, 40), (−40, 50) and (−20, 45). The solid line is the probability computed using Equation (6) with S = 1 year. Somewhat more irregular lines are the estimated probabilities based on ten years of hind-cast data.
for yearly wind speeds variability Equation (1) at four locations defined in degrees of longitude and latitude: (−20, 60), (−10, 40), (−40, 50) and (−20, 45). The solid line is the probability computed using Equation (6) with S = 1 year. Somewhat more irregular lines are the estimated probabilities based on ten years of hind-cast data.
3. Velocity of a Wind Storm
A storm occurring at time t is a region where![]() , e.g. u =
15 m
/s. The border of a storm is a u-level contour
, e.g. u =
15 m
/s. The border of a storm is a u-level contour![]() . The border changes as storms move, grow or fall. In a classical paper [7] Longuet- Higgins has introduced velocities to study movements of random surfaces. There are several definitions of velocities proposed in the literature, see [8] . Here we will use velocity in a fixed direction θ, say. The direction θ will be called the main azimuth of a storm. It will be defined in Remark 2, see also Example 1. As customary we use the convention that the direction south to north has azimuth θ = 0 while azimuth α = 90˚ for the direction west to east.
. The border changes as storms move, grow or fall. In a classical paper [7] Longuet- Higgins has introduced velocities to study movements of random surfaces. There are several definitions of velocities proposed in the literature, see [8] . Here we will use velocity in a fixed direction θ, say. The direction θ will be called the main azimuth of a storm. It will be defined in Remark 2, see also Example 1. As customary we use the convention that the direction south to north has azimuth θ = 0 while azimuth α = 90˚ for the direction west to east.
Following [8] the velocities in the direction θ and θ − 90˚ are given by
![]() (7)
(7)
where Wt is the time derivative of the wind speed, ![]() and
and ![]() are the directional derivatives having azimuths θ, θ − 90˚, respectively. These are evaluated at a position p on the u-level contour. Note that time t is fixed.
are the directional derivatives having azimuths θ, θ − 90˚, respectively. These are evaluated at a position p on the u-level contour. Note that time t is fixed.
The general assumption of this paper is that parameter a does not depend on time and changes much slower in space than the wind speed W varies, see Figure 2. Hence the gradient ![]() can be approximated as follows,
can be approximated as follows,
![]() (8)
(8)
where ![]() is the gradient of X-field. Hence velocities defined in Equation (7) can be approximated by
is the gradient of X-field. Hence velocities defined in Equation (7) can be approximated by
![]() (9)
(9)
For a homogeneous Gaussian field the velocities have median values equal to
![]() (10)
(10)
see [8] for proof. The speeds in directions θ and θ − 90˚ will be denoted by![]() ,
, ![]() , respectively. The azimuth θ is chosen in such a way that the directional derivatives
, respectively. The azimuth θ is chosen in such a way that the directional derivatives![]() ,
, ![]() are uncorrelated, see Remark 2 for some discussions about the choice of θ.
are uncorrelated, see Remark 2 for some discussions about the choice of θ.
Remark 2 The angle θ depends on properties of the covariance matrix Σ of the gradient![]() . Means to estimate the matrix Σ are given in Appendix 3. For several reasons, see [9] for detailed discussion, it is convenient to rotate the coordinate system so that the partial derivatives Xx and Xy become uncorrelated.
. Means to estimate the matrix Σ are given in Appendix 3. For several reasons, see [9] for detailed discussion, it is convenient to rotate the coordinate system so that the partial derivatives Xx and Xy become uncorrelated.
Let Aθ be the rotation by angle θ around the t-axis matrix making covariance between Xx and Xy zero. Then let denote by ![]() the covariance matrix of the
the covariance matrix of the ![]() in the rotated coordinates viz.
in the rotated coordinates viz.
![]() (11)
(11)
where ![]() is the transpose of
is the transpose of![]() . Now the
. Now the ![]() is the the element having index
11 in
the matrix
is the the element having index
11 in
the matrix ![]() while
while ![]() has index 13. Using the elements the median velocity
has index 13. Using the elements the median velocity ![]() in Equation (10) can be computed once the matrix
in Equation (10) can be computed once the matrix ![]() has been evaluated.
has been evaluated.
Example 1 Let consider the following field
![]() (12)
(12)
where![]() ,
, ![]() and
and![]() ,
, ![]() are independent variables having Rayleigh, uniform CDF, respectively, and hence X is a sum of two independent Gaussian fields. The first component is a harmonic wave moving along the x-axis with velocity L/T while the second term can be interpreted as colored noise.
are independent variables having Rayleigh, uniform CDF, respectively, and hence X is a sum of two independent Gaussian fields. The first component is a harmonic wave moving along the x-axis with velocity L/T while the second term can be interpreted as colored noise.
Obviously Xx is independent of Xy and hence θ = 90˚, see Remark 2. Further
![]()
while ![]() and hence the median velocities Equation (10) are given by
and hence the median velocities Equation (10) are given by
![]()
In this simple example the median velocities agree with the velocity of the harmonic wave moving along the x-axis.
In Figure 6, variability of the median velocities ![]() and
and ![]() in Equation (10) is compared. In the top plots seasonal variability of
in Equation (10) is compared. In the top plots seasonal variability of ![]() is illustrated by showing differences between the velocities in February and August. The maximal mean speed in the top plots is about
45 km/h
while minimal is zero. Similar comparison for the velocity
is illustrated by showing differences between the velocities in February and August. The maximal mean speed in the top plots is about
45 km/h
while minimal is zero. Similar comparison for the velocity ![]() is given in the bottom plots, where the maximal speed is about
19 km/h
. Generally one can say that the storms move faster in winter than in summer, and the angle θ also changes between the seasons. For example, in the North Atlantic the storms move basically in average from west to east while in the summer months the direction is opposite in latitude of around 20 degrees.
is given in the bottom plots, where the maximal speed is about
19 km/h
. Generally one can say that the storms move faster in winter than in summer, and the angle θ also changes between the seasons. For example, in the North Atlantic the storms move basically in average from west to east while in the summer months the direction is opposite in latitude of around 20 degrees.
4. Statistics of Encountered Wind Speeds
Main subject of the paper is development of a simple model describing variability of wind speeds time series encountered by a vessel or at a fixed location. In this section we will define the model and give means to estimate the long-term CDF of encountered winds; expected duration and strength of an encountered storm.
A ship route is a sequence of positions pi, say, a ship intends to follow. We assume that a ship will follow straight lines between the positions having azimuth![]() , say. A voyage starts at time s and will last for S days. Initial position
, say. A voyage starts at time s and will last for S days. Initial position![]() , azimuths
, azimuths ![]() and ship speeds
and ship speeds![]() ,
, ![]() , define its position
, define its position ![]() at any time t during a voyage. Then the encountered wind speeds are given by
at any time t during a voyage. Then the encountered wind speeds are given by
![]() (13)
(13)
A ship sailing along a route![]() ,
, ![]() , has velocity
, has velocity
![]()
Figure 6. Top―Estimates of the median velocities, km/h, the windy field moves in direction θ in February and August. The color corresponds to speed. The highest speed (orange) is
45.1 km/h
while the lowest (blue) is
0 km/h
. Bottom―Comparisons of the median velocities vθ − 90˚ in February and August. The highest speed is
18.6 km/h
.
![]() (14)
(14)
where ![]() is the ship speed at time t. (Recall that the x axis has azimuth 90˚ while the y-axis has azimuth 0˚.) In the following we will use the transformed Gaussian field Equation (2) to model the encountered wind speeds
is the ship speed at time t. (Recall that the x axis has azimuth 90˚ while the y-axis has azimuth 0˚.) In the following we will use the transformed Gaussian field Equation (2) to model the encountered wind speeds![]() , viz
, viz
![]() (15)
(15)
The process ![]() is Gaussian with mean
is Gaussian with mean ![]() and variance
and variance![]() , respectively.
, respectively.
The long-term CDF of encountered wind speeds is defined by
![]() (16)
(16)
The CDF given in Equation (16) could be be estimated by fitting an appropriate distribution to available data. (Weibull distribution is often used.) Alternative approach is to compute the theoretical CDF, viz.
![]() (17)
(17)
4.1. Distributions of Storm Characteristics
Similarly as in Section 3 we will say that a ship encounters stormy conditions at time t if wind speed ![]() exceeds some fixed level u. (In the examples we will use u =
15 m
/s.) Similarly, it encounters windy weather conditions at time t if wind speed is above the median, i.e.
exceeds some fixed level u. (In the examples we will use u =
15 m
/s.) Similarly, it encounters windy weather conditions at time t if wind speed is above the median, i.e.![]() . In Figure 7 wind speeds encountered along a route in October are presented. The upper intervals mark times in storms while the lower intervals show the periods of windy weather encountered by a vessel. The thin line, shown in the lower plot, illustrates variability of the encountered median wind speed.
. In Figure 7 wind speeds encountered along a route in October are presented. The upper intervals mark times in storms while the lower intervals show the periods of windy weather encountered by a vessel. The thin line, shown in the lower plot, illustrates variability of the encountered median wind speed.
The region of stormy conditions consists of time intervals when the wind speed is constantly above threshold u. The intervals will be called storms. Then let Nu denote the number of encountered storms. For example,
![]()
Figure 7. Illustration of the definition of stormy, windy weather regions. Top―A route taken in October; Bottom―Solid thick line shows the on- board measured wind speeds. The thin solid line presents variability of the median wind speed along the route. The intervals plotted at level
15 m
/s represent times when ship encounters the stormy weather while intervals plotted at level zero marks the encountered windy weather regions.
![]() in Figure 7. The durations of storms are denoted by
in Figure 7. The durations of storms are denoted by![]() , while the highest wind speed during a storm by
, while the highest wind speed during a storm by![]() ,
,![]() . The probability distributions of the characteristics will be defined next. In order to efficiently write down the formulas for the CDFs we need some additional notation introduced next.
. The probability distributions of the characteristics will be defined next. In order to efficiently write down the formulas for the CDFs we need some additional notation introduced next.
Let the number of encountered storms for which event (statement) A is true be denoted by![]() . For example,
. For example, ![]() is the number of encountered storms for which wind speeds exceed a threshold w, while
is the number of encountered storms for which wind speeds exceed a threshold w, while ![]() is the number of storms that last longer than t. Obviously
is the number of storms that last longer than t. Obviously![]() , since all
, since all![]() , is the number of upcrossings of level u by the encountered wind speeds. The empirical probability that a storm last longer than t hours can now be written as follows
, is the number of upcrossings of level u by the encountered wind speeds. The empirical probability that a storm last longer than t hours can now be written as follows
![]()
Next the theoretical, based on model, probability of event A, e.g.![]() , will be defined by
, will be defined by
![]() (18)
(18)
The proposed model Equation (15) will be validated by comparing the empirical distribution of storms strength Ast and the average durations of storms with theoretically computed ![]() and
and![]() . More complex storms statistics could also be used to validate the model but it would require a dedicated numerical software, see e.g. [10] and references therein, to evaluate
. More complex storms statistics could also be used to validate the model but it would require a dedicated numerical software, see e.g. [10] and references therein, to evaluate![]() . Hence it will not be used here. In the following only a simple bound
. Hence it will not be used here. In the following only a simple bound
![]() (19)
(19)
introduced in [11] , and the expectations
![]() (20)
(20)
will be used for validation purposes. In Equation (20), Tcl denotes time period when wind speed is uninterruptedly below the threshold u, i.e. a time period between storms. The Equation (20) will be proved in Appendix 2.
In order to evaluate Equation (19) and Equation (20), the formula for ![]() is needed. The expected number of upcrossings of level w by We can be computed using the generalized Rice’s formula [12] , viz.
is needed. The expected number of upcrossings of level w by We can be computed using the generalized Rice’s formula [12] , viz.
![]() (21)
(21)
see also [13] . Here ![]() is the time derivative of
is the time derivative of![]() .
.
Remark 3 Consider a stationary Gaussian process X with mean m and variance![]() . Let Nw be the number of upcrossings of level w by X in time interval of length S then classical result of Rice [12] gives
. Let Nw be the number of upcrossings of level w by X in time interval of length S then classical result of Rice [12] gives
![]() (22)
(22)
Consequently the average distance between upcrossing of the mean level m by X is
![]() (23)
(23)
4.2. Evaluation of ![]()
From definition of the encountered wind speed process We it follows that the number of upcrossings of the level w by ![]() in the interval
in the interval ![]() is equal to the number of upcrossings of the level
is equal to the number of upcrossings of the level ![]() by
by![]() . Since we are primarily interested in modeling wind fields in offshore locations we assume that the field is homogeneous in a region with radius of about
100 km
and stationary for a period of couple of weeks. (The assumptions are likely to fail in close to coast or inland locations.) Under the assumption
. Since we are primarily interested in modeling wind fields in offshore locations we assume that the field is homogeneous in a region with radius of about
100 km
and stationary for a period of couple of weeks. (The assumptions are likely to fail in close to coast or inland locations.) Under the assumption ![]() and
and ![]() and
and ![]() are independent. Consequently the integral in Equation (21) can be written in a more explicit way, viz.
are independent. Consequently the integral in Equation (21) can be written in a more explicit way, viz.
![]() (24)
(24)
In the following we shall use an additional parameter ![]() defined by
defined by
![]() (25)
(25)
and write Equation (24) in an alternative form
![]() (26)
(26)
Note that if Xe is stationary, then![]() , seen Equation (23). Hence
, seen Equation (23). Hence ![]() is the average time period that windy conditions last for. Properties and means to evaluate
is the average time period that windy conditions last for. Properties and means to evaluate ![]() using physically interpretable parameters are discussed in Appendix 1.
using physically interpretable parameters are discussed in Appendix 1.
5. Validation of the Model
The proposed model is validated by investigating the accuracy of the theoretically computed distributions with the empirical distributions estimated from data. Firstly at fixed positions p the theoretical statistics of the storm characteristics Ast, Tst and Tcl will be compared with estimates of the statistics derived using ten years of hind- cast data. Secondly, the long-term wind speed distributions encountered by vessels are compared with the theoretically computed distributions using the model and the estimates derived from the hind-cast. The expected number of encountered upcrossing will also be used in the validations. However statistics of encountered storm characteristics will not be used in the validation process. This is because the wind speeds measured on-board ships are biased by captains’ decisions to avoid sailing in heavy storms, reported also in [14] . Some validations of the model at inland locations was presented in [15] .
5.1. Distributions of Storm Characteristics Ast, Tst and Tcl at a Fixed Position
Consider a buoy at position p then![]() . The parameter
. The parameter![]() , see Equation (25), is then given by
, see Equation (25), is then given by
![]() (27)
(27)
In Figure 8 values of the parameter ![]() evaluated using Equation (27) for February and August are presented. In offshore locations
evaluated using Equation (27) for February and August are presented. In offshore locations ![]() is less than two days, which is much shorter than the stationarity period assumed to be about 3 weeks. Hence the parameter
is less than two days, which is much shorter than the stationarity period assumed to be about 3 weeks. Hence the parameter ![]() is the expected time period the wind speeds exceeds the median and that
is the expected time period the wind speeds exceeds the median and that ![]() is approximately constant for about a month.
is approximately constant for about a month.
The values![]() , presented in Figure 8, will be first used to validate the approximation of probability that a storm observed at position p will have wind speeds exceeding a level w > u =
15 m
/s, i.e. formula Equation (19). Next by combining formulas Equation (20) with Equation (16) and Equation (24) the expected duration of a storm will be computed and then compared with the observed average durations. The expected duration of calmer weather, i.e. time intervals when winds speeds are constantly below the threshold u, will be computed in a similar way and then used in the validation
, presented in Figure 8, will be first used to validate the approximation of probability that a storm observed at position p will have wind speeds exceeding a level w > u =
15 m
/s, i.e. formula Equation (19). Next by combining formulas Equation (20) with Equation (16) and Equation (24) the expected duration of a storm will be computed and then compared with the observed average durations. The expected duration of calmer weather, i.e. time intervals when winds speeds are constantly below the threshold u, will be computed in a similar way and then used in the validation
The probabilities ![]() and expectations
and expectations![]() ,
, ![]() are computed for a period
are computed for a period ![]() year and positions p marked by crosses in Figure 2. The results presented in Figure 9 and Table 1 show very good agreement between the observed storm characteristics at the four locations and the theoretically computed characteristics.
year and positions p marked by crosses in Figure 2. The results presented in Figure 9 and Table 1 show very good agreement between the observed storm characteristics at the four locations and the theoretically computed characteristics.
![]()
Figure 8. Comparison of spatial variability of![]() , defined in Equation (25) for a buoy. (Top) February, (Bottom) August.
, defined in Equation (25) for a buoy. (Top) February, (Bottom) August.
![]()
Table 1. Long-term (one year) expected storm/calm durations in days.
5.2. Validation-Wind Speeds Encountered by Vessels
Measurements of the wind speed over ground, i.e. ten minutes averages, recorded each ten minutes on-board some ships, are used to validate the proposed model. Since the data are recorded much denser than the hind-cast we have removed high frequencies from the signals (periods above 1.5 hour were removed using FFT). The data used in this study is limited to the North Atlantic and western region of Mediterranean Sea. The accuracy of the theoretically computed long-term distribution of encountered wind speed will be investigated.
First a single voyage operated in late August, shown in the top left plot of Figure 10, is considered. In right top plot of the figure, the measured wind speeds, shown as solid line, are compared with the estimated wind speeds using hind-cast, dashed dotted line. One can see that the two signals are reasonably close.
In the left bottom plot of Figure 10, ten thin lines show the empirical long term probabilities ![]() computed for hind-cased based estimates of wind-speeds that would be encountered if the ship were sailing the same route every year. One of the estimates is not visible since it is very close to the
computed for hind-cased based estimates of wind-speeds that would be encountered if the ship were sailing the same route every year. One of the estimates is not visible since it is very close to the ![]() estimated using the on-board measured wind speed, the thick solid line. The ten estimates show large variability between years. The regular solid line is the theoretically computed
estimated using the on-board measured wind speed, the thick solid line. The ten estimates show large variability between years. The regular solid line is the theoretically computed![]() . It is close to the average of the ten estimates derived from the hind-cast (not shown in the figure). We conclude that for the considered route the theoretical long-term distribution of wind describes well long-term variability of winds along the route. Similar conclusions can be drawn from Figure 11 left plot were the combined long-term distributions for all 40 voyages are
. It is close to the average of the ten estimates derived from the hind-cast (not shown in the figure). We conclude that for the considered route the theoretical long-term distribution of wind describes well long-term variability of winds along the route. Similar conclusions can be drawn from Figure 11 left plot were the combined long-term distributions for all 40 voyages are
shown. Based on the results presented in Figure 10 and Figure 11, we conclude that the theoretical long term distribution of wind speeds encountered by a sailing vessels agrees well with the distribution derived using hind- cast; and secondly that the routing systems used in planning a route is successful in selecting routes with calmer wind conditions than average one.
In Figure 10, bottom right plot, and in Figure 11, right plot, estimates of ![]() based on hind-cast (dashed dotted line) and the observed Nw (the solid irregular line) are compared with the theoretical
based on hind-cast (dashed dotted line) and the observed Nw (the solid irregular line) are compared with the theoretical ![]() computed using Equation (24) for routes shown in Figure 1 and Figure 10 top left plot. One can see that the lines are close except for the high wind speeds. The observed crossings of high wind speeds (solid irregular line) are fewer than theoretically predicted. This we attribute to use of routing programs that successfully choose calmer roots than the average one. This claim is also supported by studies of the estimate of
computed using Equation (24) for routes shown in Figure 1 and Figure 10 top left plot. One can see that the lines are close except for the high wind speeds. The observed crossings of high wind speeds (solid irregular line) are fewer than theoretically predicted. This we attribute to use of routing programs that successfully choose calmer roots than the average one. This claim is also supported by studies of the estimate of ![]() derived from 10 years of hind-cast, shown as the dashed line. One can see that these estimates are higher than on-board observed Nw for wind speeds above
12 m
/s.
derived from 10 years of hind-cast, shown as the dashed line. One can see that these estimates are higher than on-board observed Nw for wind speeds above
12 m
/s.
6. Simulation of the Encountered Wind Speeds
Common experience says that wind speeds vary in different time scales, e.g. diurnal patten due to different temperatures at day and night; frequency of depressions and anti-cyclones which usually occur with periods of about 4 days and annual pattern. To follow the claim the transformed observed wind speed field ![]() is decomposed into four parts which contain periods above 40 days, between 40 and 5 days, between 5 and 1 day and the noise. For each field variances
is decomposed into four parts which contain periods above 40 days, between 40 and 5 days, between 5 and 1 day and the noise. For each field variances ![]() and the covariance matrices of the gradient vector
and the covariance matrices of the gradient vector ![]() were estimated, i.e. the transformed Gaussian model fitted.
were estimated, i.e. the transformed Gaussian model fitted.
Now for any voyage one can compute parameters![]() , then independently simulate the encountered four components along a ship route. Adding the components gives simulation of
, then independently simulate the encountered four components along a ship route. Adding the components gives simulation of ![]() and finally transformation
and finally transformation
![]() gives simulated wind speeds that could be encountered along a route.
gives simulated wind speeds that could be encountered along a route.
More precisely, for a ship route![]() ,
, ![]() , one finds parameters
, one finds parameters![]() ,
, ![]() ,
, ![]() and
and![]() ,
, ![]() , then
, then ![]() is simulated by
is simulated by
![]() (28)
(28)
Here ![]() are independent Brownian motions while the kernels
are independent Brownian motions while the kernels ![]() are given by
are given by
![]()
The process ![]() is Gaussian with mean
is Gaussian with mean ![]() and the covariance function given by
and the covariance function given by
![]() (29)
(29)
Obviously the integrals in Equation (28) have to be computed numerically. This is carried out using the following approximation
![]() (30)
(30)
where Zij, ![]() , are independent zero mean variance one Gaussian random variables, while
, are independent zero mean variance one Gaussian random variables, while![]() . Here sj forms an equidistant grid covering the domain of the kernel
. Here sj forms an equidistant grid covering the domain of the kernel![]() . (In the case when wind speeds are simulated on very dense grid then it is recommended to slightly smooth the parameters
. (In the case when wind speeds are simulated on very dense grid then it is recommended to slightly smooth the parameters![]() ,
, ![]() and
and![]() .)
.)
The proposed model gives means for efficient simulation of wind speeds along any ship routes. The parameters![]() ,
, ![]() ,
, ![]() and
and ![]() are specified by means of Equation (28) and Equation (30). Alternatively one can simulate
are specified by means of Equation (28) and Equation (30). Alternatively one can simulate ![]() using covariances defined in Equation (29) and some of many methods to simulate Gaussian vectors. The algorithm based on Equation (30) is preferable when densely sampled wind speeds along a long ship route are needed. For example, for a route defined in Figure 12 top plot that was sailed for 400 hours giving 2400 recorded wind speeds, it took less than 100 seconds on laptop to simulate 100 wind speed profiles along the route. Five of the simulated profiles of
using covariances defined in Equation (29) and some of many methods to simulate Gaussian vectors. The algorithm based on Equation (30) is preferable when densely sampled wind speeds along a long ship route are needed. For example, for a route defined in Figure 12 top plot that was sailed for 400 hours giving 2400 recorded wind speeds, it took less than 100 seconds on laptop to simulate 100 wind speed profiles along the route. Five of the simulated profiles of ![]() are presented as thin solid lines in
are presented as thin solid lines in
![]()
Figure 12. Top―A route sailed in Northern Atlantic in April; Middle―The expected length of encountered windy weather period![]() ; Bottom―Wind speeds measured on-board a vessel (solid thick line) hind-cast prediction (dashed dotted line) and five simulations of the wind speeds by means of Equation (15) and Equation (28) (thin solid lines).
; Bottom―Wind speeds measured on-board a vessel (solid thick line) hind-cast prediction (dashed dotted line) and five simulations of the wind speeds by means of Equation (15) and Equation (28) (thin solid lines).
Figure 12 bottom plot. The measured wind speeds are presented as the solid thick line while dashed dotted line is the hind-cast based estimate of the speeds.
Note that parameters ![]() and
and ![]() are simply computable from the parameters
are simply computable from the parameters![]() ,
, ![]() alone. Hence the theoretical long-term distributions and statistics of storm characteristics can be computed by means of methods discussed in previous sections.
alone. Hence the theoretical long-term distributions and statistics of storm characteristics can be computed by means of methods discussed in previous sections.
7. Conclusion
A statistical model for the wind speed field variability in time and over large geographical region has been proposed. The model was fitted to ERA Interim reanalyzed data. Validation tests show very good match between the distributions estimated from the data and the theoretical computed one from the model. The model was also used to estimate risk of encountering extreme winds and the theoretical estimates agree well with the empirical one. Realistic wind profiles can be simulated using the model.
Acknowledgements
Support of Chalmers Energy Area of Advance is acknowledged. Research was also supported by Swedish Research Council Grant 340-2012-6004 and by
Knut
and
Alice
Wallenberg
Stiftelse
. The authors also would like to thank Wallenius Lines AB for providing us with onboard wind measurement data.
Appendix 1: Computation of ![]()
The parameter ![]() was defined in Equation (25), viz.
was defined in Equation (25), viz.![]() . In order to evaluate
. In order to evaluate ![]() one needs to introduce a time dependent gradient vector
one needs to introduce a time dependent gradient vector ![]() and the vector of derivatives
and the vector of derivatives
![]() (31)
(31)
Obviously ![]() and
and![]() , where ∙ is the scalar product. Hence
, where ∙ is the scalar product. Hence
![]() (32)
(32)
where ![]() is the covariance matrix of the gradient vector
is the covariance matrix of the gradient vector![]() . The matrix
. The matrix ![]() has to be estimated in the region of interest. In Appendix
3 a
sketch of the estimation procedure is given. In the following we shall give an alternative formula for
has to be estimated in the region of interest. In Appendix
3 a
sketch of the estimation procedure is given. In the following we shall give an alternative formula for ![]() which employs a physically interpretable parameters which could be useful for comparison of suitability of a trade for use of wind sails or other means to harvest wind energy.
which employs a physically interpretable parameters which could be useful for comparison of suitability of a trade for use of wind sails or other means to harvest wind energy.
Parameter ![]() as a Function of Wind, Ship Velocities and Geometrical Sizes of Windy Regions
as a Function of Wind, Ship Velocities and Geometrical Sizes of Windy Regions
The variance ![]() is independent of the choice of coordinate system. Here we will use the rotated coordinate system by azimuth
is independent of the choice of coordinate system. Here we will use the rotated coordinate system by azimuth ![]() called in Section 3 main azimuth of a storm. The matrix
called in Section 3 main azimuth of a storm. The matrix ![]() in the rotated coordinate system will be denoted by
in the rotated coordinate system will be denoted by ![]() and has the following diagonal elements
and has the following diagonal elements
![]() (33)
(33)
and following off-diagonal elements
![]() (34)
(34)
The ships velocity ![]() is in the rotated coordinates given by
is in the rotated coordinates given by
![]()
Obviously ![]() and after some algebra
and after some algebra
![]() (35)
(35)
where the encountered velocity, e.g. the difference between the ship velocity and the wind field velocity is, in the rotated coordinates, given by
![]() (36)
(36)
In order to interpret components in Equation (35), we need to introduce some additional parameters that describe average size of windy weather regions and some irregularity factors.
Recall that windy weather conditions region at time t is the region consists all p where wind speeds exceeds the median![]() . Now we shall introduce parameters related to average size of windy region in directions θ and θ − 90˚. The parameters will be denoted by
. Now we shall introduce parameters related to average size of windy region in directions θ and θ − 90˚. The parameters will be denoted by ![]() and
and![]() , respectively. The third parameter T is the average period the windy weather last lasts at a fixed position p. The parameters are defined by
, respectively. The third parameter T is the average period the windy weather last lasts at a fixed position p. The parameters are defined by
![]() (37)
(37)
see Equation (22) and Remark 3. Obviously the values of parameters are slowly changing functions of position and time and that why we call them local sizes of windy regions. However if the field ![]() were homogeneous and stationary then the parameters would be equal to the average length between upcrossings and downcrossing of the median by wind speed W in direction θ, θ + 90˚ and in time, see [9] for details.
were homogeneous and stationary then the parameters would be equal to the average length between upcrossings and downcrossing of the median by wind speed W in direction θ, θ + 90˚ and in time, see [9] for details.
Now by multiplying both sides of the Equation (35) by ![]() and dividing by
and dividing by![]() , we obtain that
, we obtain that
![]()
where
![]() (38)
(38)
are useful irregularity factors. Roughly, smaller values of the factors higher risks of extreme storms, see [9] for more details. Further, if ![]() then the surface X drifts, viz
then the surface X drifts, viz
![]()
If p has rotated coordinates then ![]() in rotated coordinates is equal to
in rotated coordinates is equal to![]() . Finally
. Finally
![]() (39)
(39)
For a homogeneous wind field ![]() is the reciprocal of the average time spend in windy weather region when sailing with azimuth θ, similar interpretation can be given to
is the reciprocal of the average time spend in windy weather region when sailing with azimuth θ, similar interpretation can be given to ![]() while T is the average time the windy weather is observed by a ship at rest or a buoy. These parameters can be estimated from the on-board measured signals or given subjective values based on experience. Usefulness of Equation (39) and Equation (24) lies in possibility of predicting risks for encountering extreme storms using easily available parameters which have clear physical meaning.
while T is the average time the windy weather is observed by a ship at rest or a buoy. These parameters can be estimated from the on-board measured signals or given subjective values based on experience. Usefulness of Equation (39) and Equation (24) lies in possibility of predicting risks for encountering extreme storms using easily available parameters which have clear physical meaning.
Appendix 2: Proof of Equation (20)
Let assume that ![]() is a smooth process. Using Fubinni’s theorem
is a smooth process. Using Fubinni’s theorem
![]()
Since![]() , where
, where ![]() is the indicator function of the set A taking value 1 if
is the indicator function of the set A taking value 1 if ![]() and zero otherwise. Again by Fubini’s theorem
and zero otherwise. Again by Fubini’s theorem
![]()
and hence
![]()
Appendix 3: Estimation of Parameters
The parameters of the model have been fitted for the North Atlantic. Here the ERA Interim data has been used, although in future work we plan to also use data from satellite based sensors. A moment’s method and regression fit were employed to estimate the parameters. In this section we give a short description of the applied estimation procedure. In the following the measured wind speeds at a location will be denoted by![]() .
.
Step 1: For a fixed geographical location and ![]() the transformed wind speed
the transformed wind speed ![]() is computed and the mean Equation (3) fitted using LS regression. Empirical cumulative distribution function (CDF) and Gaussian (CDF) are fitted to the residual
is computed and the mean Equation (3) fitted using LS regression. Empirical cumulative distribution function (CDF) and Gaussian (CDF) are fitted to the residual![]() . Parameter a* minimizing the distance between the two distributions is selected as an estimate of a. The corresponding mean
. Parameter a* minimizing the distance between the two distributions is selected as an estimate of a. The corresponding mean ![]() is an estimate of
is an estimate of![]() . Further the
. Further the
residual ![]() is evaluated and then used to estimate parameters
is evaluated and then used to estimate parameters ![]() in the following steps.
in the following steps.
Step 2: Estimation of signals![]() ,
,![]() . The signal x1 is estimated as follows; first one filters out from
. The signal x1 is estimated as follows; first one filters out from ![]() (see Step 1) the harmonics with periods shorter than 40 days. The resulting signal is an observation of
(see Step 1) the harmonics with periods shorter than 40 days. The resulting signal is an observation of![]() . The signal
. The signal ![]() is derived by filtering out harmonics with periods below 5 days from the signal
is derived by filtering out harmonics with periods below 5 days from the signal![]() . The signal
. The signal ![]() is derived by filtering out harmonics with periods below 1 day from the signal
is derived by filtering out harmonics with periods below 1 day from the signal![]()
![]() . Finally,
. Finally,![]() .
.
Step 3: For a signal ![]() the parameters
the parameters ![]() are estimated as follows. For a sequence of times tj, assuming stationarity of
are estimated as follows. For a sequence of times tj, assuming stationarity of ![]() for s in a neighborhood of 10 days around tj, estimates of
for s in a neighborhood of 10 days around tj, estimates of ![]() are found. Then
are found. Then ![]() are estimated by fitting seasonal components, similar to Equation (3), to sequences of observa-
are estimated by fitting seasonal components, similar to Equation (3), to sequences of observa-
tions![]() .
.
Step 4: Estimation of![]() , i.e. the covariance matrix of the gradient vector evaluated at
, i.e. the covariance matrix of the gradient vector evaluated at![]() . The covariance matrix is defined by six covariances between the partial derivatives of Xi. The functions are changing slowly with season but spatial variability can be high, particularly at coastal and inland locations. Consequently we fit six seasonal components to the covariances for each of positions p on a grid with mesh 0.75 degree. The components are estimated in a similar way as discussed in Step 3.
. The covariance matrix is defined by six covariances between the partial derivatives of Xi. The functions are changing slowly with season but spatial variability can be high, particularly at coastal and inland locations. Consequently we fit six seasonal components to the covariances for each of positions p on a grid with mesh 0.75 degree. The components are estimated in a similar way as discussed in Step 3.