1. Introduction
The packing model of the nucleons in an atomic nucleus always arouses curiosity of many scientists and amateurs. The model determines the shape of a nucleus as well as its various properties, such as the stability, the magnetic moment, the spin, the binding energy and radioactivity. Sophisticated theories of nuclear model were established and many facts were well explained [1] [2] . However, there is obviously still a mysterious veil on some characteristics of nuclei to be revealed, especially the packing structure of nucleons inside a nucleus. Thanks to X-ray diffraction, chemists know plenty of details about how atoms pack to build a molecule. Molecular structure establishes the basis of modern chemistry. However, since nuclei are too small and are usually embedded in electron “cloud”, it is very hard to “see” them.
In nature, the equilibrium shape of a centered direction-independent object is a sphere. These objects vary vastly in composition and size, including planets, liquid droplet, bubble, most nucleoli in cell, crystalline spherulite, latex micelles, isolated atoms (at least those which can be packed in cubic lattices) and possibly some elementary particles. A plant leaf is far from a sphere because the petiole to the stem and the surface toward the sun are very direction-related. The non-sphere shape of a molecule comes from the direction-related chemical bonds. Many atomic nuclei are generally not sphere and may possess remarkable non-zero quadrupole moment [2] . That means tha the nucleons, protons (P) and neutrons (N) are bound in specific direction and are packed in a particular structure. In this paper, the authors try to propose a model that depicts the packing of nucleons in a nucleus based on the conception of covalent molecule configuration.
2. The Binding of Proton and Neutron in a Nucleus
From the reported data [3] -[5] , there are 7 isotopes of hydrogen, or single-P nuclides: 1H, 2H, 3H, 4H, 5H, 6H and7H. In addition, reported single-N nuclei include 2H, 3He, 4Li, 5Be and 6B. This gives a clue that N, as well as P, can be a 6-coordinate center bound with 6 “ligands” at maximum as shown in Figure 1(a), where the proper octahedral structure seems to be a right way to ensure the ligands to be indistinguishable. Although these structures need to be further verified, especially the 90˚ triangular 3H and 3He, it is obvious that, in the case of single center, when the “coordination number” is higher than 2, the isotope will be unstable and tends to kick out the excess P or N.
Based on these structures, we assume that P can only bind with N and vice versa (considering deuterium, PN, is stable, but there is no conclusive evidence about the existence of NN and PP). The “bond distance” between bound P and N, DNP, is in the range of 1 to 2 fm, and the “bond angle” for 3 continuous nucleons is 90˚ or 180˚.
The single-center nuclei are characterized by extremely low binding energy EB (and therefore a low EB/A), even for the stable nuclei as 2H and 3He, noted in Figure 1(a) comparing with other nuclei. This is probably because of the existence of suspending open P or open N. Therefore, we assume that, for a nucleus with ratio of N:P = 1, open nucleon should be avoided and all P, as well as all N, should be equivalent. Thus, P and N should be bound alternatively to form a ring. It is obviously that the ring is not shaped like a pearl necklace on neck; instead, the ring must fold somehow, like a necklace in casket. The most possible way of folding a ring is taking a “bond angle” of 90˚ for every 3 continuous nucleons, to ensure the nuclide to adopt the densest packing and the most nearly sphere symmetrical shape. However, for most nuclei, the ratio of N/P is more or less than unit. Among hundreds of stable nuclei, only 12 are composed purely of a ring: 4He, 6Li, 10B,
12C
, 14N, 16O, 20Ne, 24Mg, 28Si, 32S, 36Ar and40Ca. Thus, extra N(‘s) or extra P(‘s) will be necessary to connect or insert the ring somehow in most nuclei.
3. Ring Structure
Based on the “ring plus extra nucleon” hypothesis, the shape of 4He should be a square, which is the smallest ring. Figure 1(b) demonstrates the shapes and EB of nuclei of the P2N2 family, where the extra open N generally contributes very little to EB, while extra open P generally gives minus contribution. Thus, in the P2N2 family, all the nuclei which possess open nucleon are unstable. In addition, the EB and life time of P2N2+X are always in larger number than P2+XN2. This corresponds to the fact that stable nuclei present a ratio N/P ≥ 1(except 3He).
In Figure 1(b), some nuclei may have 2 or more isomers, for example, 5He may have 2 isomers, 6He 3, 7He 6 and so on. It is reasonable to assume that favored structure should be the highest symmetry and the most compact. It should be noted that, for saturating the 6 coordinates, 12He will be the possibly heaviest isotope of helium (10He is the maximum found). For the same reason, for elements of Z = 7 to 10, 9N, 10O,
11F
and 12Ne will be the possibly lightest isotopes respectively, which have not been found yet.
Figure 2 gives the possible shapes of some light rings and their stable isotopes. For odd-Z rings, although
![]()
Figure 1. The possible shapes of (a) single-P nuclides (isotopes of H) and single-N nuclides (from 1n to
7C
), (b) nuclides based on P2N2 ring. Black ball stands for P and white one for N (same in following figures). EB (in MeV, in parenthesis), main decay mode and the daughter isotope are marked beside each nuclide.
there are a few possibilities and more when Z becomes large, a common feature is that the gravity centers of P and N are separated and are eccentric to the gravity center of nuclide. This can be easily proved mathematically. In addition, one can always find one or more arrangement with antisymmetric center, through which each P can find an N by space reflection and vice versa. We assume that the most possible odd-Z ring structure is antisymmetric and the most densely packed. For 7Li and other nuclei, the extra N may not likely bind to a ring P as an open N like unstable nuclides of P2N2 family. Instead, when 2 or more ring P’s are geometrically available to share an extra N with 90 “bond angles” and same DPN, the extra N tends to be stable. It seems this is the most likely way the extra N combines with the ring considering the geometric arrangement and indistinguishableness of N’s. Actually, among all stable nuclei, the ratio of N/P is in the range of 1.00 to 1.54 (208Pb), that means ring P is able to stably bind a little more than 0.5 extra N (or 2 ring P’s share one extra N) at maximum, while no extra P can stably bind to ring N. This is the reason that, in the P2N2 family, all the nuclides with extra P or extra N are unstable because of the valence limitation of the square shaped ring. From the shape of the ring structure, one can predict the possibly heaviest and the lightest isotopes of the related elements. As an example, based on P3N3 ring, the possibly heaviest isotope of lithium is 16Li and the possibly lightest isotope of aluminium is 16Al. For other elements, the possibly heaviest and lightest isotopes can also be predicted if the structure of related ring is known.
The possible packing structures of some light even-Z rings and their stable isotopes are also shown in Figure 2. By contrast to odd-Z rings, all the even-Z rings possess a superimposed gravity center of P and N, which was tested by hundreds of examples without any exception and is destined to be proved mathematically. In addition,
![]()
Figure 2. The possible structures of some light nuclides based on “ring plus extra nucleon” model. For odd-Z nuclides (above), the gravity centers of P and N (gP and gN) are eccentric and the rings are antisymmetrical. For even-Z nuclides (below), gP and gN are superimposed, while the rings are center symmetrical and are indistinguishable when P and N interchange. The extra N is highlighted in gray and bond in dot-line. 8Be in frame is impossible because it is non center symmetrical and geometrically unavailable for any stable extra N.
some of the structures are center-symmetrical. We assume that the most possible ring structure of even-Z nuclei is the most densely packed one with center-symmetry and is indistinguishable when all P and N interchange. In Figure 2, the framed
12C
is marked “impossible” because it mutates to another structure when P and N interchange. It is interesting to find that 8Be is composed of two P2N2 squares and is ready to yield into two α-particles. Only 9Be, with an extra N that bridges two squares by the manner mentioned above, is stable. Therefore, as another restriction, the most possible ring structure should avoid the arrangement that can split into two normal rings.
Because of the symmetrical and geometrical restrictions of ring structure, empty open space in a large nucleus (Z > 20) is unavoidable. An important function of extra N is to fill the open space, making the nuclide packed more densely and establishing adequate non-bond interaction. Figure 3 shows the nuclide size, characterized by radius of gyration, [R2]0.5 (as defined in the following equation) versus the nucleon number A. The points of stable nuclides locate around the line of slope = 1/3, or the nuclide volume is roughly proportional to A. In addition, one can find a general trend that, for rings, the radius expands related to the line with Z increases due to the open space (16O is special possibly because of double magic numbers, which will be revealed in future).
From the possible structures shown in Figure 2, one can figure out that if nuclei possess too many N’s to be bind properly by 2 or more ring P’s, some open N will be unavoidable as a neutron halo and the nucleus will be unusually large, such as 11Li in Figure 2. This is qualitatively accordant with the scattering cross-section observations for extremely N-rich nuclides [6] .
4. Binding Energy per Nucleon
The EB/A for all the PxNx rings, in Figure 4, display a zigzag feature, where even-Z rings are at the vertex and odd-Z rings at the nadir. As mentioned earlier, the fundamental difference for even-Z and odd-Z ring is that the former has superimposed gravity centers of P and N, while the later is eccentric. It is obvious that eccentricity results in lower EB, which is possibly because the eccentric nucleus inside an atom requires more energy to spin faster to avoid the surrounding electrons to “feel” uneven.
It is well known that EB/A of the isotopes of an element displays a specific zigzag feature, where the vertex always relates odd A for odd-Z elements, and relates even A for even-Z elements, as shown in the examples (26Fe and 29Cu) in Figure 4. Weizasäcker’s semi-empirical mass formula treated this feature by a selective function, f5 in an ad hoc way [2] .
In this work, the degree of eccentricity, Sg, is defined as the separation of the gravity centers of P and N, Dg(PN), over 2 times the radius of gyration, [R2]0.5,
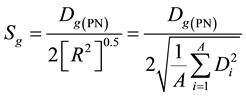
![]()
Figure 3. Radius of gyration vs A for rings (in light gray) and their stable isotopes (in black) of some light nuclei (Z = 2 to 9).
![]()
Figure 4. EB/A of ring nuclides PZNZ. The zigzag feature implies a fundamental difference between odd- and even-Z rings. The envelope line for even-Z ring is shown, with which the depression energy by eccentricity, ΔEec, for odd-Z ring is defined. Embededis zigzag feature of EB/A (above) and Sn (below) for even-Z elements (26Fe as an example) and odd-Z elements (29Cu as an example). ΔEec for PZNZ+1(even-Z) is defined.
where Di is the length from i’th nucleon to the gravity center of the nucleus. For any even-Z ring, Sg is always zero because Dg(PN) = 0; while for odd-Z rings, Sg is higher than 0. From the definition, deuterium, 2H, has the highest Sg of 1. For other light odd-Z rings, such as 6Li and 10B, Sg is also quite high, and therefore leads up to a very low EB. The depression of EB/A by eccentricity, ΔEec, is defined in Figure 4 for some simple odd-Z rings and even-odd nuclides. The relationship between Sg and ΔEec is demonstrated in Figure 5. It should be noted that this relationship is not very quantitative because ΔEec is also affected by non-bond interactions of a particular nuclide as will be mentioned later.
Cohesive interactions between metallic atoms are mostly governed by their electron configuration. Since the high Sg means the high nuclear “polarity”, which provides an extra interaction between isolated atoms, like polar molecules have higher intermolecular interactions than nonpolar ones. That can explain Li, Be and B respectively demonstrate the unusually highest melting point and boiling point in their group (similar electron configuration) of periodic table.
To understand the zigzag feature, Figure 6 depicts the Dg(PN) and eccentricity Sg shift caused by extra nucleon in different cases, that results in fluctuation of EB/A exactly as the way as the rings or isotopes of any element do (vertex for even Z at even A while odd Z at odd A).
The envelope line of EB/A for even-Z rings in Figure 4 demonstrates that, without the energy depression by eccentricity, EB/A increases from very low for light Z ring to maximum at P28N28, and then decreases slowly. This should be due to the variation of non-bond interaction.
For most elements, EB/A of a ring, as basic structure, is not the highest among the isotopes, as the examples shown in Figure 4. It is because extra N, which fills the open spaces in large ring and builds adequate non-bond interaction, may lead to higher EB/A and stability. Nevertheless, special stability of ring structure can be detected
![]()
Figure 5. Relationship between degree of eccentricity, Sg, and depression energy by eccentricity, ΔEec, for eccentric nuclides. The ΔEec of odd-Z ring (in light gray) and even-Z nuclide PZNZ+1 (in black) are defined in Figure 4.
![]()
Figure 6. The explanation of EB/A zigzag feature of nuclei. Even-Z ring has superimposed gravity centers of P (tiny black dot) and N (tiny white dot); while odd-Z ring has eccentric gravity centers. Extra N or P shifts the gravity centers and therefore Dg(PN) as well as ΔEec fluctuates.
in many facts. Weizasäcker formula includes a symmetry term f4 emphasizing PZNZ is more favored in energy [2] . This can also be shown in Figure 4 that, except P-rich nuclides, PZNZ always possesses the highest one-N separation energy, Sn (for most odd-Z nuclei the highest is PZNZ+1 because of lower eccentricity). That is to say, N in a ring structure is generally more stable than extra N. Since extra P is much more unstable, the normal extra nucleons can only be N or P, excluding N and P.
Basically, EB/A of a nucleus is governed by many factors. Strong force between binding P and N in a ring plays the most important role, up to about 7 MeV (as in 4He), which should be equal for all rings. The weak force acts between non-bond nucleons (P..N, N..N and P..P) in a ring that provides higher EB/A up to 8.5 MeV (as in 40Ca). The open spaces hinders non-bond interaction, and makes nuclide very unstable even EB/A is not so low. The extra N shared by 2 or more ring P’s, which contributes similar strong force, provides more weak force and, therefore, can increase EB/A up to 8.8 MeV (as in 62Ni). When ring is too large, the open spaces may not be completely filled by extra N, and EB/A lowers gradually. Eccentricity is an important factor that decreases EB especially for light nuclei as depicted in Figure 5. In addition, excess extra N or P can only connect to the ring as open nucleons, which have very little or minus contribution to strong force and thus result in many very unstable nuclei with very low EB/A. Because of the complicated effects, the nuclide shapes shown in Figure 2 are only the most possible arrangements and need to be confirmed or revised by new theory considering more details of nuclear forces and new experimental observations.
5. Mirror Nuclei
Mirror nuclei are the pair of nuclides PX+nNX and PXNX+n. Some correlations of the pair have been reported since long ago [7] -[10] . The most remarkable fact is the identical spin and parity, Jπ, of mirror nuclei in ground state as summarized in Table 1, with very few exceptions or uncertainties. Since the ring is indistinguishable when P and N interchange, any nuclide with n extra N(¢s) will have a counterpart with n extra P(¢s) in similar way of binding to the ring. Thus, the shapes of the pair nuclides are similar but P and N interchange, just like a black-white photo and the negative film. This should be the basic reason for the following equation.

It is also reasonable to predict the identity of degree of eccentricity for the pair.

7Be is present in the atmosphere in trace amount [11] as the only natural occurring radioisotope with the ratio of N/P < 1. As the mirror nuclide of 7Li, 7Be has an extra P and can also obtain a large energy bonus from the highest eccentricity in 6Li although, as expectation, 7Be is still not stable enough as 7Li.
Figure 7 demonstrates the EB/A of mirror nuclei. It is clear that the EB/A of PXNX+n is always larger than that of PX+nNX. Compared with the zigzag feature of ring PXNX mentioned earlier, when n is odd, the curves are smooth because odd extra P or N diminishes the depression energy by eccentricity for odd-X nuclides. Of course, when n is even, the curves zigzag again. In addition, it is notable that the difference of EB/A for any pair is nearly a constant: averagely 0.179, 0.368, 0.559, 0.763, 0.926 and 1.084 MeV for n = 1, 2, 3, 4, 5 and 6 respectively (the curves for n = 5 and
6 a
re omitted in Figure 7). This can be described with following equation.
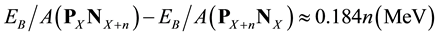
In summary, the ring plus extra nucleon model seems properly meet the structure requirement to the correlations of mirror nuclei.
6. Conclusion
A nucleus PXNY (X, Y ≥ 2) is composed of a ring PXNX with P and N alternative binding plus Y − X extra N(¢s) if Y > X, or a ring PYNY plus X − Y extra P(¢s) if X > Y. The ring folds with a “bond angle” of 90˚ for every 3 continuous nucleons. Extra N can bound to ring-P with the same “bond angle” and “bond distance”. Extra P can bound to ring N in a similar way but the binding is weaker than that of extra P. When 2 or more ring P’s are geometrically available, the extra N tends to be stable. Excess extra N results in open N with low EB/A and neutron halo with large radius. Even-Z rings, as well as normal even-even nuclei, always have superimposed gravity centers of P and N; while for odd-Z rings, as well as odd-A nuclides, both centers of P and N must be eccentric. The eccentricity results in a depression of EB. Therefore, the zigzag features of EB/A of an element differing for odd and even Z can be simply explained by the shift of eccentricity by extra nucleons. Symmetry center may present in any even-even nuclei. While for odd-Z rings, only antisymmetry center is possible. In both cases of even and odd-Z, the rings are indistinguishable when P and N interchange. Based on the ring plus extra nucleon model, the mirror nuclei are equivalent in structure and demonstrate identical spin and parity. As the eccentricity shift, the EB/A curves of mirror nuclei display smooth when the number of extra nucleon n is odd, and zigzag
![]()
Table 1. The identical spin and parity for mirror nuclei: Jπ(PX+nNX) = Jπ(PXNX+n)*.
*Not include the mirror nuclei n > 5, which satisfy the identity as the cases in the table.
![]()
Figure 7. The comparison of EB/A for mirror nuclei with the number of extra nucleon n = 1, 2, 3 and 4 (from top to bottom). For each case, the EB/A difference between mirror nuclei is nearly a constant. When n = 1, 3, the curves are smooth; when n = 2, 4, they become zigzag.
when n is even. The EB/A difference between the pair is nearly a constant of 0.184n MeV.
Acknowledgements
The authors thank Prof. Jubo Zhu and Prof. Jianshu Luo for their effort in mathematical proof as well as many valuable discussions with Qinghua Wang, Tianjiao Hu and Zhenghua Jiang.
Methods
1. The nucleon coordinates (x, y, z) for the nuclei in Figure 2
(P: bold, N: normal, extra N: in parenthesis)
6Li 0,0,0 & 1,1,0 & 0,1,1 & 1,0,0 & 1,1,1 & 0,0,1
7Li ibid & (0,1,0)
11Li ibid & (2,1,0) & (0,1,2) & (0,-1,0) & (1,2,0)
10B 0,0,0 & 1,0,1 & 2,1,1 & 1,2,1 & 1,1,0 & 1,0,0 & 1,1,1 & 2,2,1 & 1,2,0 & 0,1,0
11B ibid & (0,0,1)
14N 0,0,0 & 0,1,1 & 1,0,1 & 2,1,1 & 3,1,0 & 2,0,0 & 1,1,0 & 0,0,1 & 1,1,1 & 2,0,1 & 3,1,1 & 3,0,0 & 2,1,0 & 1,0,0
15N ibid & (0,1,0)
18 F
1,0,0 & 2,0,1 & 3,1,1 & 2,1,0 & 2,2,1 & 1,3,1 & 0,3,0 & 1,2,0 & 1,1,1 & 2,0,0 & 3,0,1 & 2,1,1 & 2,2,0 & 2,3,1 & 1,3,0 & 0,2,0 & 1,2,1 & 1,1,0
19 F
ibid & (1,0,1)
8Be 0,0,0 & 1,1,0 & 2,1,1 & 1,0,1 & 1,0,0 & 2,1,0 & 1,1,1 & 0,0,1
9Be ibid & (2,0,1)
12 C
1,0,0 & 2,1,0 & 3,1,1 & 2,2,1 & 1,1,1 & 0,1,0 & 2,0,0 & 3,1,0 & 2,1,1 & 1,2,1 & 0,1,1 & 1,1,0
13 C
ibid & (1,0,1)
16O 1,0,0 & 2,0,1 & 2,1,0 & 3,1,1 & 2,2,1 & 1,2,0 & 1,1,1 & 0,1,0 & 1,0,1 & 2,0,0 & 3,1,0 & 2,1,1 & 2,2,0 & 1,2,1 & 0,1,1 & 1,1,0
17O ibid & (0,0,0)
18O ibid & (3,2,1)
The coordinates are determined according to the rules:
1) Even Z ring nuclei are center-symmetrical, indistinguishable when P and N interchange.
2) Odd-Z ring nuclei are antisymmetrical.
3) Avoid the structures that may split into two normal rings if possible.
4) Be of smallest radius of gyration [R2]0.5.
5) Extra N is bound by 2 or more ring P’s, high abundance isotopes are generally bound by 3 P’s.
2. The proof: “odd-Z rings have separated gravity centers of P and N”
A ring with ZP’s and ZN’s is arranged as P-N alternating connections in Cartesian coordinate, where the distance between two bound nucleons is 1 unit, and the adjacent connection lines perpendicular to each other. Let any of a P be A1 at (0,0,0), while A2 (an N) is at one of 6 possible coordinates: (±1, 0, 0) or (0, ±1, 0) or (0, 0, ±1).
For any Ai, the Equations (1) and (2) must be satisfied.
 (1)
(1)
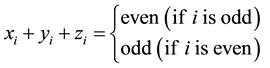 (2)
(2)
when Z is an odd number, if the gravity center of P (i = 1, 3, 5, ・・・, 2Z − 1) were superimposed with that of N (i = 2, 4, 6, ・・・, 2Z), the following equations must be satisfied.
Then, the necessary condition for the superimposition is
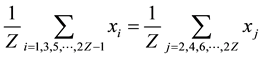 (3)
(3)
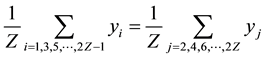 (4)
(4)
![]() (5)
(5)
Adding Equations (3), (4) and (5), the resulted Equation (6) is the necessary condition for the superimposition.
![]() (6)
(6)
However, the left side of Equation (6) must be even, while the right side must be odd. Obviously, the Equation (6) is impossible. Therefore, for odd Z ring, the gravity centers of P and N must be separated.
3. Calculation of gravity center of n nucleons, xg, yg and zg
![]()
4. Calculation of radius of gyration of a nucleus with A nucleons
![]()
xg, yg and zg are the coordinate of gravity center of the nuclide.
5. Calculation of the separation of gravity centers of P and N
![]()
xg, yg and zg with subscript (P) and (N) are the coordinates of gravity center of all P’s and all N’s in a nucleus respectively.
NOTES
*Corresponding author.