An Efficient Method for Epileptic Seizure Detection in Long-Term EEG Recordings ()
1. Introduction
1.1. Medical Background and Medications
An epileptic seizure is a transient occurrence of electrical hyperactivity in different parts of the brain produces physical symptoms such as short periods of inattention and loss of memory, a sensory hallucination, or a whole body convulsion. Epileptic patients are suffering from unpredictable, persistent and frequent seizures that limit the independence of them, increase the risk of serious injury, resulting in social isolation and economic hardship. Causes of epilepsy vary from a brain injury, tumor, stroke, genetic mutations and any problems in the brain from a previous infection [1] [2] . Electroencephalogram (EEG) is the recording of the brain’s electrical activity by electrodes attached to the scalp (scalp EEG) or through special electrodes implanted in the brain (intracranial EEG). Scalp EEG is the most common and widely used clinical procedure for diagnosing, monitoring and managing the neurological disorders related to epilepsy [3] . Brain functioning affects the morphology of EEG [4] . Spikes in EEG are usually an indication of abnormal functioning of the brain and highly correlated with epilepsy [5] . For identification of these rapid epileptiform waveforms, neurophysiologists must go through (quantitative) EEG data via his/her naked eye to identify such abnormalities. Visual examination of long EEG recordings is challenging as well as tiresome, tedious, laborious and too time consuming. Thus, automatic spike detection attempts have received intense attention, urgently required to limit such difficulties of the traditional EEG examination. This study presents a method to detect three spike types that usually appeared in epileptic EEG.
1.2. Related Work
Over the years, several algorithms have been developed for detection of spikes, sharp waves and other transient signals in scalp EEG. A great and venerable contribution has been given by Dr. Rajeev Yadav and his team, presenting new methods for automatic seizure detection and spike sorting, helping us to understand the nature of EEG, particularly its rapid changes at the beginning and during seizures [6] [7] . The following paragraph highlights their prominent work in this field:
In [8] , R. Yadav, et al., proposed a new algorithm for seizure detection using frequency-weighted energy. The method performance was evaluated using 100 hours of a single channel stereo encephalograms (SEEG) obtained from five different patients, resulting 96.6% and 0.21/h of sensitivity and false detection rate respectively. An overall improvement has been achieved in terms of sensitivity, specificity and FDR in [9] , by using a dual-stage classifier applied for 300 hours of SEEG recordings obtained from fifteen patients. In [10] , a patient-specific model for seizure detection method has been proposed using statistically optimal null filters. This method was relied on a priori known seizure (template patterns) for subsequent detection of similar seizures in EEG data for seven patients. In [11] , a novel morphology-based classifier (with simple computations appropriate to real-time applications) to identify sharp waves in intracranial EEG was presented. The method detects various types of seizures (rhythmic, non-rhythmic, short and long-seizures) with a sensitivity of 100%, a false detection rate of 0.1/h and an average onset delay of 9.1 s. In terms of spike detection and sorting, a spike classification algorithm combining template matching and principal component analysis (PCA) was proposed in [12] . Using intracranial EEG from 5 patients, the method resulted in 82.1% of the detected spikes in non-overlapping and disjoint clusters. In the literature review, Oikonomou, et al., in [13] and Alexandros T. Tzallas, et al., in [14] summarized the most techniques used to detect spikes in EEG signal. The EEG signal is characterized by rapid dynamics that instantly change through distinctive stages before (preictal), during (ictal), and after (post ictal) a seizure [15] . This nonlinearity nature and fast transitions between non-seizure, pre-seizure, and seizure states, guide researchers to a promising solution by combining two or more techniques to capture the EEG features in multiple domains, where epileptic spikes could be recognized by its characteristics in wide feature spaces. Therefore, two techniques that analyze the EEG signal in temporal and spatial or temporal and frequency domains were combined in previous detection methods [16] . Our method presented in this work, is extensive so that; it recognizes three types of epileptic spikes in a broad framework including more than one domain. Our algorithm was designed to proceed sequentially in short windowing epochs of the tested data, to suspend its rapid dynamics and capture any morphological fluctuation through distinctive states before, during, and after seizures.
1.3. Epileptic Spikes
Two significant states are involved during the seizure evolution: ictal (during seizure) and inter-ictal (between seizures). In inter ictal period, the signal is characterized by certain morphologies, including isolated spikes, sharp waves, poly spikes and wave complexes (spikes followed by slow waves forming spike-and wave complex) last from 20 to 200 ms, while these abnormalities extend to 150 - 350 ms during ictal states [3] [13] [14] . Wave complexes, isolated and poly spikes are the typically observed patterns in epileptic EEG [17] [18] . So, in this work, we focused on these three spike types that generally seen in the majority of epileptic patients. The wave complexes are a spike followed by a slow wave occurring at rates below 3 Hz [19] , with duration from 150 to 350 ms [3] [13] . Isolated spikes usually appear alone and clearly distinct from the background activity by a sudden rise in amplitude with a duration varying from 20 to 70 ms [13] . The third epileptiform pattern is the poly spike which consists of several sequenced spikes followed by slow waves [20] , at a frequency of 3 - 6 Hz [17] .
1.4. Proposed Approach
Our approach comprises two steps:
1) Derivation of template models for three epileptic spikes; Epileptic complex spike (ECS), Epileptic isolated spike (EIS) and Epileptic poly spike (EPS).
2) Analogizing (comparing) various features of the predefined templates against the same features extracted from a sequenced window of the raw EEG data under analysis.
Mainly, spectral, spatial and frequency-temporal features were analyzed to detect similar windows of the raw data to any epileptic spike templates (ECS, EIS and EPS). Lomb-Scargle Transform (LST), Independent Component Analysis (ICA) and Daubechies Wavelet (Db4) are provided to extract features that will be analogized via a simple technique called “Cosine Similarity”. Firstly, the Cosine Similarity measure is used as a pre-classifier in a manner that; if there are similarities (according to specified threshold for each characteristic) between the tested window and any template, the tested window is suspected to contain an epileptic spike. Secondly, to avoid spike deception (reducing the false detection rate), a variable threshold determined by Mean Squared Error (MSE) is applied, to decide either the tested window is an epileptic spike or a noisy background.
2. Materials and Methods
This study was conducted in the Clinical Neurophysiology Unit, Kasr El Aini Hospital, Faculty of medicine, Cairo University. The data used for this research were obtained from epileptic patients who had been under evaluation and treatment in the Clinical Neurophysiology Unit. The patients were diagnosed as they suffered from different epilepsy types. Through this study, all international ethical committees was taken into account, the patients were notified and agreed to conduct this study on their EEGs. The EEG was recorded using scalp electrodes according to the International 10 - 20 system.
2.1. Data Acquisition
Two real EEG data sets were used during development procedures and performance evaluation of the method. These data are the following:
1) Dataset 1 (for extracting epileptic spikes)
By the close investigation of many epileptic EEG recordings (containing various morphologies of spikes, sharp waves, spike and-wave complexes, poly spike-and-wave complexes), neurophysiologists were requested to identify only three epileptic spike types. Each spike type was marked along its duration. Several patterns for each spike type was picked up and separated into discrete segments of 350 msec. A template model for each spike type is estimated based on these extracted segments.
2) Dataset 2 (for testing)
The data were collected from 15 epileptic patients and allocated for training and performance evaluation of the method.
2.2. Pre-Processing and Artifact Rejection
The noises in EEG are called artifacts that should be removed for proper analysis and minimize their influence in the feature extraction stage. These artifacts are generated from the body itself (bio artifacts) or caused by external interferences. Bio artifacts are originating from non-cerebral sources as EMG, EOG and ECG but may be detected by an EEG machine. External artifacts are occurring during recording due to bad electrodes, baseline movement, electrical power line (50/60 Hz), mobile interference…To minimize the influence of these artifacts, an analog anti-aliasing filter and a band-pass Butterworth filter (with sampling frequency 200 Hz and cut-off frequencies of 0.1 - 100 Hz) were used to remove linear trends, attenuate channel drifts and improve the reliability of ICA decomposition.
2.3. Template Derivation
To perform a certain template, suitable epochs corresponding to each spike type were picked out by qualified neurophysiologists from epileptic EEG recordings. The width of each segment was 350 msec (70 samples) to include a whole epileptiform discharge (clear spike) and its instantaneous background. The template for each epileptic spike (ECS, EIS, and EPS) is estimated as the median of its separated segments, (mostly, 115 - 120 segments were selected for each spike type).
2.4. Feature Extraction
2.4.1. Independent Component Analysis (ICA) and Wavelet Transform (WT)
Independent Component Analysis (ICA) is a recent technique to separate statistically independent components from a mixture of data [21] . ICA can be used to decompose the signal into spatio-temporal independent components, giving important information about the spatial and temporal features of the signal [22] [23] . Kobayashi et al., in [24] [25] [26] has illustrated that, the scalp EEG can be decomposed by ICA into components with fixed potential field distributions (spatial components) and maximally independent time waveforms (temporal components), indicating that, ICA performs better than Principal Component Analysis (PCA) in this task. Moreover, the epileptic transients (as spikes) can be separated from the background, (since each transient having a slightly different generator geometry, very small time delay and jitter), concluding that the scalp distribution of the epileptic components obtained by ICA contains important spatial information about the generator sources of epileptiform discharges. The results in [25] indicate that the spatial components of epileptic discharges (extracted by ICA) could be powerful to identify the location of epileptic generator sources of the scalp. Details of algorithms to extract the spatial components by ICA are described in [24] [27] . Briefly, let x(t) denote a vector of n observed signals x at time t;
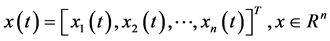 (1)
(1)
where, x(t) is a mixture of m unknown sources s;
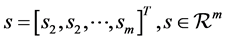 (2)
(2)
To obtain the temporal independent components Y, produced by m sources, ICA estimates a separating (unmixing) matrix W such that;
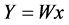 (3)
(3)
Equation (3) implies that;
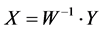 (4)
(4)
Onton, et al., in [27] has shown that; the resulting ( ), i.e. the product of the ith column of inverse matrix (
), i.e. the product of the ith column of inverse matrix (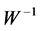 ) and the ith row of Y, is a portion of the original data (X) that forms the spatial independent components (
) and the ith row of Y, is a portion of the original data (X) that forms the spatial independent components (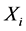 ), and the whole data (X) are the sum of these ICs (
), and the whole data (X) are the sum of these ICs (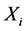 ),
),
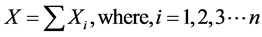 (5)
(5)
Thus, the columns of the inverse matrix (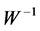 ) contain relative weights (spatial features) by which each independent component (
) contain relative weights (spatial features) by which each independent component (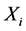 ), could be projected back into the scalp, forming what is called IC scalp map. In other words, each column of the inverse matrix (
), could be projected back into the scalp, forming what is called IC scalp map. In other words, each column of the inverse matrix (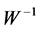 ) represents the relative projection weight where the independent components (ICs) denote its source locations on the scalp at each electrode of a single component source [27] . Consequently, in our method, it was suggested that; by comparing the spatial components (
) represents the relative projection weight where the independent components (ICs) denote its source locations on the scalp at each electrode of a single component source [27] . Consequently, in our method, it was suggested that; by comparing the spatial components ( ) for both the tested EEG window (segments of the signal under analysis) and each spike template (according to an appropriate threshold), waveforms that resemble any of spike templates (ECS, EIS and EPS) along the tested EEG signal could be recognized. However, the performance can be improved by extracting more features in other spaces beside that extracted by ICA. Recently, researchers have advised combining both Wavelet (WT) and ICA to exploit their benefits which complement each other [28] . Wavelet Transform (WT) gives a macroscopic vision by decomposing the signal into its constituent frequency bands at different time localizations, according to the desired scale’s resolution [16] . For a conventional mother wavelet
) for both the tested EEG window (segments of the signal under analysis) and each spike template (according to an appropriate threshold), waveforms that resemble any of spike templates (ECS, EIS and EPS) along the tested EEG signal could be recognized. However, the performance can be improved by extracting more features in other spaces beside that extracted by ICA. Recently, researchers have advised combining both Wavelet (WT) and ICA to exploit their benefits which complement each other [28] . Wavelet Transform (WT) gives a macroscopic vision by decomposing the signal into its constituent frequency bands at different time localizations, according to the desired scale’s resolution [16] . For a conventional mother wavelet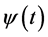 , the Discrete Wavelet Transform (DWT) at scale “a” and position “b”, is defined as;
, the Discrete Wavelet Transform (DWT) at scale “a” and position “b”, is defined as;
 (6)
(6)
where, a and b are discrete values based on powers of two, ![]() , j and k are integers, the function
, j and k are integers, the function ![]() is determined as;
is determined as;
![]() (7)
(7)
By varying “b”, the wavelet function ![]() is replaced into the desired point of time, while capturing the high and low-frequency components of the signal as increasing and decreasing “a” respectively. So, at different locations of time, the frequency details of the signal can be obtained at several scales. Hence, both frequency and time features of fast transients in the EEG signal can be extracted from its WT coefficients, ignoring the nonstationary nature of the signal [29] . For DWT, many wavelet families are available as Haar, Daubechies, Symlets, Coiflets, … The quality of the features extracted by WT is mainly depends on the choice of a convenient “mother” wavelet and the number of decomposed sub-bands (WT coefficients) [18] [29] [30] [31] . After inspecting several types of traditional mother wavelets, practical experiments have demonstrated that; Daubechies wavelet of order 4 (Db4) is more appropriate for our application. Fortunately, Db4 has been strongly recommended for EEG spike detection by many researchers in precedent works [29] [30] [31] [32] [33] . The Db4 produces the highest correlation coefficients with the epileptic spikes [30] [31] because of its orthogonality [29] and smoothing properties that allow identifying fast alterations in EEG signals [34] . Since the EEG signals do not have any useful frequency components above 30 Hz [33] [34] , and some types of seizures are predominant mainly in the delta frequency band (Delta waves) [18] , the Db4 was performed at 5 levels to obtain the desired frequency resolution. Hence, both the tested EEG windows (segments of raw EEG data under analysis) and each of the epileptic spike templates (ECS, EIS and EPS) were decomposed into 6 sub-bands: 5 details (D1 - D5) and one approximation (A5). In current work, to detect similar spikes in the tested windows to any template (ECS, EIS and EPS), an appropriate vector of features could be extracted from their WT coefficients and compared according to a particular threshold for each template. So the maximum, minimum, mean, and standard deviation for each of the four WT coefficients (D3 - D5 and A5) were computed and set out as the feature vectors. Also, following the work presented by Ling Guo et al. in [35] , the line length was used as another feature, since it is sensitive to amplitude-frequency variations [36] and its low computational time. The five extracted features from sub-bands; (D3 - D5 and A5) for the three epileptic spike templates (ECS, EIS and EPS) showed the significant differences between them and allowed us to detect similar spikes along the data under test to any of spike templates, with a considerable accuracy as will be discussed in the results section.
is replaced into the desired point of time, while capturing the high and low-frequency components of the signal as increasing and decreasing “a” respectively. So, at different locations of time, the frequency details of the signal can be obtained at several scales. Hence, both frequency and time features of fast transients in the EEG signal can be extracted from its WT coefficients, ignoring the nonstationary nature of the signal [29] . For DWT, many wavelet families are available as Haar, Daubechies, Symlets, Coiflets, … The quality of the features extracted by WT is mainly depends on the choice of a convenient “mother” wavelet and the number of decomposed sub-bands (WT coefficients) [18] [29] [30] [31] . After inspecting several types of traditional mother wavelets, practical experiments have demonstrated that; Daubechies wavelet of order 4 (Db4) is more appropriate for our application. Fortunately, Db4 has been strongly recommended for EEG spike detection by many researchers in precedent works [29] [30] [31] [32] [33] . The Db4 produces the highest correlation coefficients with the epileptic spikes [30] [31] because of its orthogonality [29] and smoothing properties that allow identifying fast alterations in EEG signals [34] . Since the EEG signals do not have any useful frequency components above 30 Hz [33] [34] , and some types of seizures are predominant mainly in the delta frequency band (Delta waves) [18] , the Db4 was performed at 5 levels to obtain the desired frequency resolution. Hence, both the tested EEG windows (segments of raw EEG data under analysis) and each of the epileptic spike templates (ECS, EIS and EPS) were decomposed into 6 sub-bands: 5 details (D1 - D5) and one approximation (A5). In current work, to detect similar spikes in the tested windows to any template (ECS, EIS and EPS), an appropriate vector of features could be extracted from their WT coefficients and compared according to a particular threshold for each template. So the maximum, minimum, mean, and standard deviation for each of the four WT coefficients (D3 - D5 and A5) were computed and set out as the feature vectors. Also, following the work presented by Ling Guo et al. in [35] , the line length was used as another feature, since it is sensitive to amplitude-frequency variations [36] and its low computational time. The five extracted features from sub-bands; (D3 - D5 and A5) for the three epileptic spike templates (ECS, EIS and EPS) showed the significant differences between them and allowed us to detect similar spikes along the data under test to any of spike templates, with a considerable accuracy as will be discussed in the results section.
2.4.2. Lomb-Scargle Periodogram (LSP)
A significant characteristic that discriminates epileptic spikes from other EEG waveforms is its increase in instantaneous energy [32] . Due to the nonstationary nature of EEG signals, (meaning that characteristics as mean, variance or power-spectra, change with time [37] ), detection of spikes by inspecting its spectrum in time-domain, is not preferable. Since the amplitude and spectrum of spikes vary from signal to signal, subject to subject, it even varies from time to time for the same subject [32] . On the other hand, the “rhythmic” behavior of epileptic seizures that characterized by a peak in power spectrum at a specific frequencies [8] , could be used to reveal such epileptic spikes. Saini et al. [38] showed the efficiency of applying Lomb-Scargle transform (LST) for estimating the power spectrum, which could be convenient for our application. For xn, provides a vector of n observed signals x at time n, the Lomb periodogram at frequency f is defined by;
![]() (8)
(8)
where![]() ,
, ![]() are the mean and variance,
are the mean and variance, ![]() is a frequency dependent time delay defined to make the periodogram insensitive to time shift. The power spectrum of the three epileptic spike templates (ECS, EIS and EPS) estimated by LSP showed that the spectrum of each is different to the other, particularly in the frequency range up to 30 Hz. Also, the spectrum for templates are decreased to zero in the range above 30 Hz, which is reasonable since the EEG signals do not have any useful frequency components above 30 Hz [33] [34] . However, LSP is provided in this study to estimate the spectrum of the three epileptic spike templates (ECS, EIS and EPS) and each sequenced window of the raw EEG data under test. In a further stage, by analogizing the spectrum of both the tested EEG against each of the confirmed epileptic templates (ECS, EIS and EPS), (according to an appropriate threshold for each template), it is possible to quantify the similar spike to any of the epileptic templates as will be explained in the following section.
is a frequency dependent time delay defined to make the periodogram insensitive to time shift. The power spectrum of the three epileptic spike templates (ECS, EIS and EPS) estimated by LSP showed that the spectrum of each is different to the other, particularly in the frequency range up to 30 Hz. Also, the spectrum for templates are decreased to zero in the range above 30 Hz, which is reasonable since the EEG signals do not have any useful frequency components above 30 Hz [33] [34] . However, LSP is provided in this study to estimate the spectrum of the three epileptic spike templates (ECS, EIS and EPS) and each sequenced window of the raw EEG data under test. In a further stage, by analogizing the spectrum of both the tested EEG against each of the confirmed epileptic templates (ECS, EIS and EPS), (according to an appropriate threshold for each template), it is possible to quantify the similar spike to any of the epileptic templates as will be explained in the following section.
2.5. Cosine Similarity Measure
Mathematically, one to one function is that produces one specific output for each one input. The cosine function is from these functions, because each tiny angle change is accompanied by precise increment or decrement in its cosine value. This significant property can be employed to detect similarity (coincidence) between two vectors by determining the cosine of the angle between them, at different time points. Using a cosine function for such purposes is called Cosine Similarity measure. It is currently implemented in speech and face recognition, fingerprints, text, and signature investigation. Compared to other tools, simplicity, accuracy and higher resolution of Cosine Similarity (since its outcome is neatly bounded between −1 to 1), give it many preferences to detect similarity between patterns. The Cosine Similarity measure has been used in many EEG applications. For instance, in [39] , this measure is used to reject ocular artifacts (EOG) by discarding similar waveforms to EOG patterns in the tested EEG signal along different channels. By using this approach, similarity between patterns is calculated according to its vectors’ directions, making this technique appropriate for fast transients and chaotic signals as EEG. This is detailed in [40] where a new technique based on this measure was used to identify similarity between two time series, at different time locations. Powered with good results in [40] , the author recommended applying this technique for audio recognition and detecting variability of beat to beat in ECG signals. In current work, for each initial epileptic spike template (ECS, EIS and EPS), the spatial, wavelet and spectral features were extracted and ranked as N rows of an N × M matrix, then it is reshaped into an N∙M size vector, (since the length is not the same in all feature types). Thus, a specific vector feature for each template involves adequate attributes that depict its distribution over the features-plane space. Accordingly, identical procedures will be performed for each consecutive window of raw EEG data under test, to compose its vector of features. The Cosine Similarity measure decides whether the data under analysis contains similar waveforms to any spike template or not, (by identifying similarity between their vector of features, according to a specific threshold for each template).
Let the vector feature of the i-th window (of the raw EEG data under analysis), is denoted by;
![]() (9)
(9)
and
![]() (10)
(10)
is the vector feature of epileptic spike templates; ECS, EIS, and EPS, for![]() , respectively.
, respectively.
The cosine value of the angle ![]() between the vector features of i-th window
between the vector features of i-th window![]() , and j-th template
, and j-th template ![]() is;
is;
![]() (11)
(11)
To avoid the periodic nature of the cosine function, the absolute value of![]() , is determined to indicate similarity between the i-th tested window and j-th epileptic spike template. From Equation (11), the larger value represents more similarity (meaning the angle θ is close to 0˚, i.e. both vector features, Y and X are nearly coincided and matched to each other). Practically, an appropriate threshold,
, is determined to indicate similarity between the i-th tested window and j-th epileptic spike template. From Equation (11), the larger value represents more similarity (meaning the angle θ is close to 0˚, i.e. both vector features, Y and X are nearly coincided and matched to each other). Practically, an appropriate threshold, ![]() , was adopted to each template, where
, was adopted to each template, where![]() , is the angle at which similarity is verified. In detail, along the tested signal, for each template; ECS, EIS, and EPS, similar windows will be identified when, (
, is the angle at which similarity is verified. In detail, along the tested signal, for each template; ECS, EIS, and EPS, similar windows will be identified when, (![]() ), for
), for![]() , respectively. Consequently, the initial templates; ECS, EIS, and EPS with their threshold values
, respectively. Consequently, the initial templates; ECS, EIS, and EPS with their threshold values![]() , could be considered as the crucial parameters that control the total performance of the method. However, due to the wide irregularity of epileptic spikes (that vary from patient to patient, it even varies randomly for the same patient [32] ), dependence on static templates and static thresholds to detect epileptic spikes is not reliable, resulting in much of false detections. To overcome these limitations, similar windows to the initial epileptic templates (ECS, EIS and EPS), will be elected for further refinement by an adaptive model of Mean Squared Error (MSE). Through which, updated thresholds for dynamic templates will be assigned automatically according to seizure evolution. MSE is the expected value of the square error by which the i-th window
, could be considered as the crucial parameters that control the total performance of the method. However, due to the wide irregularity of epileptic spikes (that vary from patient to patient, it even varies randomly for the same patient [32] ), dependence on static templates and static thresholds to detect epileptic spikes is not reliable, resulting in much of false detections. To overcome these limitations, similar windows to the initial epileptic templates (ECS, EIS and EPS), will be elected for further refinement by an adaptive model of Mean Squared Error (MSE). Through which, updated thresholds for dynamic templates will be assigned automatically according to seizure evolution. MSE is the expected value of the square error by which the i-th window ![]() differs from the j-th template
differs from the j-th template![]() , as;
, as;
![]() (12)
(12)
If MSE of the i-th window ![]() exceeds a predefined initial threshold
exceeds a predefined initial threshold![]() , (for initial templates ECS, EIS, and EPS where
, (for initial templates ECS, EIS, and EPS where![]() , respectively) as;
, respectively) as;
![]() (13)
(13)
then, ![]() will be considered the template for the next process, while the initial threshold
will be considered the template for the next process, while the initial threshold ![]() is replaced by the MSE error of the i-th window
is replaced by the MSE error of the i-th window![]() . So, the output error is used to adapt both the templates and thresholds for the following windows of raw data under analysis. It should be noted that, along the next N-processes, the new template
. So, the output error is used to adapt both the templates and thresholds for the following windows of raw data under analysis. It should be noted that, along the next N-processes, the new template ![]() with the renewed threshold (
with the renewed threshold (![]() ), will not be refreshed unless a subsequent window
), will not be refreshed unless a subsequent window ![]() surpasses the threshold
surpasses the threshold![]() . So, both the template for each spike type and its threshold will be updated automatically, while the update is reiterated for the following N-processes, until they don’t change any more when the following condition is satisfied;
. So, both the template for each spike type and its threshold will be updated automatically, while the update is reiterated for the following N-processes, until they don’t change any more when the following condition is satisfied;
![]() (14)
(14)
where σ, is the standard deviation of the previous MSE thresholds. At that stage, the procedure will be started again with the default template ![]() and initial threshold
and initial threshold![]() . So, Cosine Similarity measure can be regarded as a pre-classification stage to avoid non-spikes waveforms and capture only similar spikes to the initial templates
. So, Cosine Similarity measure can be regarded as a pre-classification stage to avoid non-spikes waveforms and capture only similar spikes to the initial templates![]() . Then, by setting a dynamic MSE’ threshold in an adaptive way that compensates the variance of epileptic spikes (detected by Cos Sim.), the overall detection performance is increased as will be illustrated in the results section.
. Then, by setting a dynamic MSE’ threshold in an adaptive way that compensates the variance of epileptic spikes (detected by Cos Sim.), the overall detection performance is increased as will be illustrated in the results section.
3. Results
The described method was tested using EEG data set 2 mentioned above. The set contains 20 single channel EEG data files (with different lengths), were gathered by scalp EEG electrodes according to the 10 - 20 international system. These data files were collected during various stages of sleep-wake cycles, including a wide variety of epileptiform activities from 15 epileptic patients (11 males, 4 females), aged 14 - 65 years. From this data, 10 files were intermixed and randomly selected as a tested set. The performance has been evaluated according to the conventional examination by experienced neurophysiologists from Clinical Neuro Physiology Unit, Kasr El Aini Hospital, Faculty of Medicine, Cairo University, where their decision was used as the “gold standard”. In detail, during the visual investigation of the tested data, neurophysiologists were asked to mark each spike, by labeling the type, onset time and its duration. Later, the results obtained by the method were assessed based on the report made by the experts. However, the performance was also determined in terms of Sensitivity, Specificity, Selectivity and Average Detection Rate. According to this test, our method correctly identified 663 of 710 as isolated spikes, providing a sensitivity of 93.3%, a specificity of 90.1, a selectivity of 92.3 and average detection rate of 91.7%, which is the best compared to the results of the other two spike types. On the other hand, for complex spike type, the method succeeded to detect 306 of 361 with 84.7%, 88.6%, 82.2% and 86.6% in terms of sensitivity, specificity, selectivity and average detection rate respectively, while 207 of 258 were identified as poly spikes with 80.2%, 88.8%, 78.4% and 84.5% of sensitivity, specificity, selectivity and average detection rate respectively. The overall performance was 88.4% sensitivity, 89.2% specificity, 86.8% selectivity, and 88% for average detection rate when results of the three spike types were combined. The total number of missed spikes was 153. These missed spikes were reexamined by neurophysiologists and classified as 47 isolated, 55 complex and 51 poly spikes. By carefully reviewing all missed spikes, it was found that its duration ranged from 18 to 97 ms with amplitude between 90 - 176 μV. The inability to detect these short spikes is due to the width chosen for the initial templates (ECS, EIS, and EPS). Although the template length can be decreased, but it will be more sensitive to tiny artifacts and spurious spikes resulting unreasonable percentage of false detections (this was concluded after many experimental procedures on training data).
In total 178 false detections were verified and categorized by neurophysiologists as the following;
- 41 false-detections were Wicket spikes (characterized by sharp arched waveform due to temporal alpha activity).
- 24 false-detections were Vertex spikes (quite sharply repetitive waves lasting in 200 m Sec with amplitude up to 150 - 250 μV).
- 37 false-detections were due to different EEG artifacts, and only 76 false-detections were reported as false positives. According to these observations, a pleasurable percentage of false detections are more satisfactory rather than missing a true spike. However, fast computational time of the algorithm shouldn’t be ignored, on average, 2.091 Sec was required to process 600 windows of raw EEG data (3.5 min) on a 2.10 GHz, Intel Core i3 laptop.
4. Conclusion and Future Work
EEG morphology is the primary, meaningful characteristic reflects the brain activity. It can be said, each waveform in EEG is generated due to its own brain’s mechanisms that completely different from others. These mechanisms follow nonlinear and chaotic nature resulting enormous EEG waveforms. Spikes are from such EEG waveforms that play essential roles to diagnose brain disorders. Many spike types are common waveforms accompanied in epileptic EEG. Identification the presence of spikes provides vital diagnostic information in many clinical situations. Spikes are not just a sudden amplitude rise (in the time domain) distinguished from its background, but also containing underlying features in frequency and spatial domains. In this paper, we have presented a methodology to detect only three types of epileptic spikes which are isolated, wave complex and poly spikes in prolonged EEG recordings. According to results, the method achieves 88.4% sensitivity, 89.2% specificity, 86.8% selectivity, and 88% for average detection rate. While we present these results that may be promising, but at the same time, it must be remembered the algorithm performance was evaluated on limited data sets. Also, the measured parameters TP, FN, FP and TN were determined according to a visual investigation by EEG experts, utilizing the True Scan EEG system (DEYMED Diagnostic, Czech Republic), where human error during this manual inspection cannot be ignored. It is very difficult to compare our algorithm against others because the focus of this study is detecting only three spike types as a preliminary stage that will be extended for more epileptic waveforms. Besides, our tested data are different from the data used to evaluate other suggested methods, with various measurements for evaluating the performance of each method, and opinions of experts about spike patterns. From this study, we have obviously concluded that, analyzing EEG signal in a broad framework, including temporal, frequency, and spatial domains may be a good solution to capture fast EEG transients as epileptic spikes. Also, to take advantage of information and activities of adjacent channels, it is recommended that processing EEG data in a multichannel scheme can highly improve the performance rather than processing each channel individually. We will recruit this important note in the future work. In our algorithm, the three waveforms isolated, wave complex and poly spikes were chosen mainly for simplicity to employ the concept of processing EEG in more than one domain can overcome its chaotic and nonlinearity nature. Improvement of our algorithm by including extra epileptic waveforms and validation with larger data sets is our next tasks. From approval conditions of a new tool is its fast and easy use in clinical practice. So fast computational time performs very crucial advantage, especially in EEG field, where large quantity data are required to be inspected. In conclusion, according to the reasonable performance of our method, particularly the fast computation that nominates it as a simple, powerful and fast tool for offline quantitative EEG examinations, saving more time and exertion. However, in the longer run, transforming EEG processing into a comprehensive domain, including its temporal, frequency and spatial underlying features, could provide a promising platform for smart diagnostic tools for many neurological disorders.
Acknowledgements
The authors gratefully appreciate the contributions of Dr. Rajeev Yadav and acknowledge his encouragement and advice.