Does the Homogeneous Ice Nucleation Initiate in the Bulk Volume or at the Surface of Super-Cooled Water Droplets? A Review ()
1. Introduction
The formation of ice in clouds can occur through primary processes (nucleation of ice from the liquid or water vapour phases), either homogeneously or heterogeneously triggered by aerosol particles called ice nuclei (IN), as well as through secondary processes. The homogeneous nucleation process involves only pure water or solution droplets. Micrometer-sized pure water droplets should nucleate homogeneously in stationary conditions at about 235 K, but if the droplets evaporate, the freezing temperature could be higher [1] [2] . Homogeneous freezing is crucial for the microphysics in the formation of high altitude cirrus and polar stratospheric clouds, and also in the glaciation of thunderclouds, at temperatures below about 235 K [3] [4] . Cziczo et al. [5] , however, suggest that mineral dust and metallic particles are the dominant source of residual particles contained in ice crystal.
Four heterogeneous nucleation mechanisms are distinguished for atmospheric ice formation: deposition, condensation-freezing, contact-freezing, and immersion-freezing. Heterogeneous freezing occurs at lower supersaturation and higher temperatures than homogeneous freezing [6] [7] .
Secondary ice formation processes can occur through: 1) the fracturing of ice crystals exposed to dry air layers, or the collision of pre-existing ice crystals [8] [9] ; 2) the fragmentation of large individual cloud drops during freezing in free fall [10] ; and 3) the fragmentation of freezing droplets following their collision with ice particles in cloud (riming), known as the Hallett-Mossop process [11] .
Several reviews have already been published on the subject of ice nucleation in the atmosphere, which incorporate findings from field measurements, laboratory studies and modelling work [1] [12] -[16] . The present paper focuses on a bounded issue, i.e. the problem of surface and/or volume homogeneous nucleation of supercooled water droplets. Although many theoretical and experimental studies on ice nucleation in supercooled water have been performed, the physical process of homogeneous nucleation is still not well understood. The laboratory data from studies using airborne water droplets have produced nucleation rates whose temperature dependence generally agrees reasonable well [17] -[20] . Sometimes, however, there are large discrepancies among the results obtained by different studies. For instance, there is a spread of over three orders of magnitude in the values obtained at 238 K [17] [18] [21] [22] . For some time, it has been unclear whether these large discrepancies were due solely to systematic differences in the experimental techniques and/or errors, or to some deficiency in the classical volume-based approach.
The possibility of a surface nucleation process is an important point, as this process would alter the concentration and size of the ice crystals produced, as compared to volume-only nucleation scenario. This has important consequences for bulk parameterizations in numerical models, which typically employ temperature―and composition―dependent formulations for the homogeneous nucleation rate coefficient, based solely on the classical, volume approach [23] [24] . Any contribution from a surface-based process would alter the predicted characteristics of ice formation and growth, and in turn, the predicted cloud microphysical and radiative properties [25] .
2. Theoretical Approach
The common model for homogeneous freezing of a supercooled droplet assumes a two-step process, i.e. nucleation followed by growth. Nucleation is the formation of a “critical” size embryo through the whole volume, due to temperature and/or density fluctuations. Following the classical theory, nucleation originates in the interior volume of a water droplet. A sufficient quantity of water molecules must come together within the droplet to form an embryo of ice. The development of the embryo entails an energy cost for the creation of an interface between the two phases, and the existence of a minimum size, called critical cluster size, before the energy advantage of forming the thermodynamically more stable new phase overcomes the extra cost of building the interface. As soon as the first critical nucleus forms, it will grow rapidly (instantaneously on the time scale of the experiment), until the entire sample is frozen. The growth rate is much lower then the rate of nucleation. One single germ is sufficient to crystallize the complete droplet. Measuring the time the sample takes to freeze then becomes equivalent to measuring the time for nucleation to occur, i.e. the rate of nucleation is identical with the rate of the phase transition [26] -[28] .
It is generally assumed that the homogeneous nucleation rate JV, i.e. the number of nuclei formed per unit liquid water volume and time, can be modelled by an Arrhenius-type dependence:
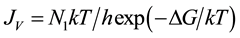 (1)
(1)
where N1 is the number of molecules per cm3 of water, T is the Kelvin temperature, k and h are the Boltzmann and Plank constants, respectively; ΔG is the work of formation of the critical cluster.
Tabazadeh et al. [29] , examining the data of Butorin and Skripov [17] , Taborek [18] , DeMott and Rogers [21] , Krämer et al. [19] and Salcedo [30] , observed that the scatter of the ice nucleation rate based on surface is much lower than the scatter in the case of a homogeneous volume-based nucleation (Figure 1 & Figure 2 of the paper). The considered data concern experiments performed with a large range of droplet diameter and in a different ways, i.e. oil emulsion, continuous slow-expansion cloud chamber, electrodynamic trap of charged microdroplets. Therefore, Tabazadeh et al. [29] suggested that the nucleation events can occur not only inside the droplets, but even on or close to the surface of water droplets.
By considering freezing events of droplets of radius r, the number of nucleation events per unit time would be given by the sum of both surface and volume processes:
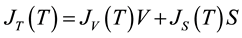 (2)
(2)
where V and S are the volume and surface area of the droplets, JS (cm−2×s−1) and JV (cm−3×s−1) represent the number of liquid-to-solid nucleation events per unit time per unit surface area or unit volume of liquid, respectively. The ice nucleation rate is strongly dependent on the temperature. It changes by 6 orders of magnitude in a temperature interval of about 4 K [19] [31] .
If , the nucleation mode is volume-initiated, whereas when
, the nucleation mode is volume-initiated, whereas when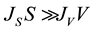 , the nucleation mode is surface-initiated.
, the nucleation mode is surface-initiated.
From Equation (2) the following expression can be obtained:
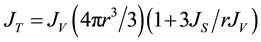 (3)
(3)
which shows that the contribution of surface freezing relative to volume freezing is proportional to r−1. Hence, surface freezing should be important for smaller radii and dominant below a certain critical radius rc = 3JS/JV , defined as the size at which surface and volume freezing are equally important [32] .
![]()
Figure 1. Ice nucleation data from experiments performed with suspended or free falling droplets in air.
![]()
Figure 2. Volume-and surface-based nucleation rate from separate models fits to small, medium and large aerosols [from Kuhn et al., 2011].
In the case of isothermal experiments with monodisperse droplets, the volume nucleation rate can be experimentally calculated from:
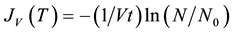 (4)
(4)
where N0 is the total number of investigated supercooled droplets, each having the same volume V, N is the number of unfrozen droplets after a time t. By plotting ln (N/N0) vs. time, it is possible to calculate directly the rate of homogeneous nucleation once the volume of the droplets is known [19] [33] .
There are several assumptions inherent in the derivation of Equation (4). It is assumed that the droplets are monodispersed and there is only one nucleation event per droplet. The number of ice nuclei forming per second therefore equals the number of droplets frozen per second. In addition, it is supposed that the crystallization growth velocity is fast, the nucleation events in different droplets are independent, and any volume element within the droplet can contribute equally to the formation of a nucleation germ. Deviations from these assumptions (e.g. preferred nucleation close to the surface) should be detectable as a change in the temporal evolution of the decay curve [33] . Assuming that the nucleation is attributed either solely to volume- or surface-initiated nucleation, Equation (4) can be rearranged by using the droplet radius, as follows:
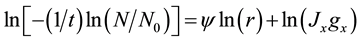 (5)
(5)
where ψ is the radial power dependence of the solidification frequency, gx is a constant related to the droplet geometry, and the suffix X is replaced by either V or S. A plot of 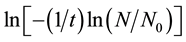 vs ln(r) for various droplet sizes will yield ψ. When volume-initiated nucleation is dominant (i.e.
vs ln(r) for various droplet sizes will yield ψ. When volume-initiated nucleation is dominant (i.e.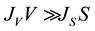 ), ψ should approach 3, while a value of 2 indicates a surface nucleation, i.e.
), ψ should approach 3, while a value of 2 indicates a surface nucleation, i.e. 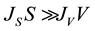 [34] [35] .
[34] [35] .
A different way to distinguish between surface and volume freezing is to study the size dependence of the homogeneous nucleation rate coefficient for droplets immersed in the same ambient bath, e.g. in experiments with small water droplets (about 1 μm), and larger ones (e.g. higher that 10 μm). If freezing is predominantly a volume process, then the volume-specific rate coefficient JV, for a given temperature, should be invariable for experiments with droplets of different size. If this is not the case, there is also a contribution of the surface nucleation. If nucleation occurs completely on the surface, the surface specific nucleation rate should be size independent [29] [32] .
The freezing rate for surface nucleation should strongly depend on the droplet size and surface contamination. Therefore, anthropogenic activity could influence the freezing rates of cloud droplets, with important implications for atmospheric composition and the radiative balance of the Earth. Surface nucleation of small droplets will influence the formation of cirrus clouds, altering the concentrations and size of ice crystals that would be produced as compared to volume-only nucleation scenario. This has potentially important ramifications for bulk parametrizations in numerical models, which employ temperature- and composition? dependent formulations for the homogeneous nucleation rate coefficient based solely on the classical, volume-based approach [23] [24] . Any contribution from a surface-based process will alter the predicted characteristics of ice formation and growth, and in turn, predicted cloud microphysical and radiative properties.
3. Reported Data
Nucleation rates in supercooled water have been measured by several groups using different experimental techniques: expansion cloud chambers [21] [36] [37] , on glass cover slip with a hydrophobic coating [38] [39] , in water-in-oil emulsions [17] [18] [34] [35] , levitation methods [19] [40] , free falling droplets [25] [32] [34] , supersonic nozzles [28] , and on field measurements [41] [42] .
The data obtained from oil emulsion should be carefully considered, as the oil-water interface can interfere with the nucleation process [18] [35] . In oil ambients, depending on the oil and surfactant materials used, there could be cases where volume-based nucleation can become thermodynamically more favourable than the surface process [29] . The levitation technique has several advantages, as a liquid droplet has no common boundary with other condensed phases, as in emulsion experiments, and it is not necessary to evaluate the size distribution of an ensemble of droplets. Possible changes in the droplet size due to evaporation during the nucleation time can be measured precisely [22] .
Uncertainties could arise in the case of levitation through an electrostatic field, but no direct influence of the droplet surface charge on the nucleation rate was found [19] [33] . In the case of acoustic levitation, a dynamic nucleation of ice can be favoured due to the presence of gas bubbles in the supercooled water.
Tabazadeh et al. [43] re-analyzed the experimental data on the homogeneous freezing rates of concentrated aqueous nitric acid solution droplets, which constitute polar stratospheric clouds. They found that surface-based rate expressions are consistent with all the considered laboratory data [44] -[48] and that the homogeneous nucleation process occurring in atmospheric droplets may be a surface-rather than a volume-related rate process. The authors concluded that the rates of ice nucleation in droplets in air are higher than those observed in oil, and that surface nucleation is favoured over volume nucleation when supercooled water drops are smaller and temperature higher. Papers published before Tabazadeh et al. [29] do not address the problem of surface or volume nucleation and assume as valid the classical nucleation theory.
Figure 1 shows the results, as volume nucleation rates, of some experiments performed with suspended or free falling droplets. Duft and Leisner [49] performed an experiment with 19 and 49 μm radius droplets levitated in an electrodynamic balance. They report the nucleation rates calculated on the basis of volume and surface process. The resulting surface nucleation rates are about a factor of 2.5 apart for the two size classes, while the volume nucleation rates in the two classes are equivalent. Therefore, they concluded that, within the investigated size range, the freezing rate of supercooled water scales with the droplet volume and freezing is therefore a volume-dominated process, and that surface nucleation might only be important for much smaller particles. Krämer et al. [19] observed the freezing of single water droplets levitated inside an electrodynamic trap, in order to derive the homogeneous nucleation rate in a temperature interval between 236.1 and 237.3 K. The droplets had a radius range between 15 and 30 μm and carried a charge of 36 pC. Since the nucleation rate turned out to be, within the limit of error, independent of droplet size and charge, the authors concluded that the freezing process starts by homogeneous nucleation in the volume phase and not on the surface layer where charges are located. The observed temperature dependence of the nucleation rate follows, but lies somewhat below the curve obtained by Pruppacher [31] , derived by fitting the classical nucleation theory to all data published until 1995.
Even Stöckel et al. [22] , by examining data on the nucleation rates of pure water droplets (r ~ 45 μm; temperature range from 236.37 to 237.91 K) levitated in an electrodynamic balance, did not find any evidence of a surface mechanism being involved. The authors admit that, as cloud water droplets are much smaller than tested ones, the results “can not contribute to the argument of whether in the atmosphere homogeneous freezing of droplets occurs in the volume or on the surface”. The data are well fitted with those obtained by Stan et al. [20] with a microfluidic chip containing a monodisperse drop generator (r ~ 40 μm; temperature range from 235.35 to 237.15 K). The nucleation rates are lower than the average of all data published until 1995, reported by Pruppacher [31] . The slopes d(ln J)/dT of all the curves presented in Figure 1 are similar, with only the results of DeMott and Rogers [21] showing a weaker temperature dependence.
High speed monitoring of the freezing process of a sucrose solution droplet (r ~ 1 mm) acoustically levitated or suspended, is reported by Bauerecker et al. [50] and Hindmarsh et al. [51] . Both volume and surface ice nucleations were observed. Increased sucrose concentration caused surface nucleation to become less favourable. The results suggest that the surface-activated nucleation is a pseudo-heterogeneous process at the liquid-vapor interface.
Lü et al. [40] also investigated the nucleation of acoustically levitated water drops, finding that ice nucleation is mainly confined to the surface. In this case, the acoustic streaming around the water drop improves the heat transfer between the levitated drop and its surrounding medium, and as a result a low-temperature region is developed near the drop surface. Therefore, in this case the surface nucleation freezing may be due to lower surface temperature as compared to the inside one. As in this case the sound intensity affects the nucleation process, these results can not be applied to atmospheric conditions.
Surface nucleation was observed during freezing of evaporating droplets by Satoh et al. [52] , and Shaw and Lamb [53] , by considering drops of radius 1.5 mm and 12 - 45 μm, respectively. In these cases, the surface evaporation is favoured by the lower surface temperature.
Considering experiments performed with free falling drops, Earle et al. [25] and Kuhn et al. [32] used supercooled liquid water droplets with mean radii of 1.0, 1.7 and 2.9 μm (temperature range from 234.8 K to 236.2 K), flowing through a vertical tube equipped with copper cooling coils. A microphysical model was used to fit experimental data and to determine homogeneous freezing rates. Analysis of the size dependent freezing data confirmed that the classical, volume-based nucleation theory is valid for larger droplets. However, as the droplet size decreases, surface freezing becomes progressively more important. Surface and volume nucleation rates, following the numerical model, should become comparable for water droplets with radii of about 5 μm, with surface rates predominating at smaller sizes.
Figure 2 shows volume and surface-based nucleation rates vs. temperature obtained from the Kuhn et al. [32] model, which fits the experimental data. Error bars are shown for volume-specific nucleation rate coefficients at different temperatures. The size dependence of the freezing rates (see Figure 3 of the paper) is also consistent with findings of Duft and Leiner [49] , who used the two radii 49 and 19 μm in their experiments and concluded that the volume nucleation is dominant for those sizes. Experiments performed by Wood et al. [54] with bigger droplets (20 μm and 33 μm) free falling in a freezing tube, gave a nucleation rate independent of the radius of the droplets, in agreement with the nucleation rate data based on volume nucleation of Pruppacher [31] .
The microphysical model based on experimental measurements in the study of Kuhn et al. [32] could explain the results of DeMott and Rogers [21] , who obtained nucleation rates, based on volume nucleation, higher than values reported in experiments performed at the same temperature [17] [18] [20] . As a matter of fact, Kuhn et al. [32] , in a model developed to interpret experimental freezing data, showed an unexpected size dependence, where JV increased with decreasing aerosol size, if classical volume-based nucleation was considered in a predominantly surface freezing process.
DeMott and Rogers [21] studied homogeneous nucleation in diluted aqueous salt solution droplets, obtained through a continuous slow expansion in a cloud chamber. The droplet radius was in the 0.5 - 4 μm range. Therefore, it is likely that surface nucleation was prevalent and that the reported JV values do not comply with the actual physical process. The surface nucleation rate obtained by Kuhn et al. [32] at T = 236 K is about 103 cm−2∙s−1, a value about equal to the one obtained by converting the data of DeMott and Rogers [21] , at the same temperature, from volume to surface nucleation. The same assessment can be made for the Hagen et al. [37] data, who obtained an even higher nucleation rate than DeMott and Rogers [21] in a similar experiment performed with lower radius droplets (r ~ 0.1 μm).
Benz et al. [55] [56] report homogeneous nucleation rates based on three experiments in artificial supercooled water clouds (r ~ 3 μm), generated and cooled below the homogeneous freezing threshold of about 237.6 K, by slow expansions of humid sulphuric acid aerosols in a large chamber (AIDA). Nucleation rates measured in the 236.3 - 237.2 K temperature range varied between ~106 cm−3∙s−1 at the highest and ~108 cm−3∙s−1 at the lowest temperature, on the assumption that homogeneous ice nucleation is volume-rather than surface-dominated. At T = 237 K, the nucleation rate agreed with the value of Duft and Leisner [49] , based on a volume nucleation rate. The results are questionable, since the authors state that the concentration of ice crystals cannot be accurately determined. A very important but unknown systematic error results from the temperature measurements, which are fundamental to all nucleation rate determinations, due to the strong dependence of the nucleation rate on the temperature, and finally the data varied with exhaustion rates of the chamber. The nucleation rate in the experiments 1-2-3 differs by a factor of ten. As the water activity of the droplets studied was > 0.998, the authors concluded that the sulphuric acid content did not affect the nucleation rate.
Experiments on the ice nucleation rate in supercooled droplets were performed also on a glass cover slip, which had a hydrophobic coating in water-in-oil emulsions (Figure 3).
Taborek [18] used a calorimetric technique to measure the nucleation rate of ice in supercooled water droplets, employing emulsions stabilized by two different surfactants (STS, sorbitan tristearate; STO, sorbitan trioleate). For STS emulsions, the nucleation rate scales with the volume and seems to be determined by the properties of the bulk water, both for small (d = 6 μm) and large droplets (d = 300 μm), while STO surfactant, according to the author, catalyzed nucleation at the droplet surface. The considered surfactants gave nucleation rates that differed by more than one order of magnitude. Butorin and Skripov [17] adopted a method very similar to that of Taborek [18] . They immersed single water droplets of diameters between 20 and 500 μm in a “vacuum oil”, and observed the freezing event by means of differential thermal analysis. Wood and Walton [34] also measured nucleation rates in emulsified droplets, using optical mcroscope to monitor freezing. They reported values that are very scattered.
Murray et al. [39] nebulized ultrapure water into a glass chamber, allowing it to settle onto a glass cover slip which had a hydrophobic organosilane coating (Fluka, 5% dimethyldichlorosilane in heptane). This ensured the substrate did not interfere with ice nucleation. Two bins of 5 - 10 μm and 10 - 20 μm were considered. The authors assumed that nucleation occurs in the interior of the droplets. However, examining the data reported in Figure 4 of their paper, it appears that droplets in the 5 - 10 μm bins show higher nucleation rates, which could indicate a contribution of surface nucleation. Inada et al. [35] studied the effectiveness of antifreeze protein and poly (vinyl alcohol) in inhibiting ice nucleation in water-in-oil emulsions, where homogeneous ice nucleation can be experimentally simulated. They results showed that ice nucleation was surface-initiated, with radius droplet in the 1 - 5 μm range. The conclusion was obtained by following the criteria of Wood and Walton [34] . Ciobanu et al. [57] investigated the efflorescence of ammonium sulphate (AS) in micrometer-sized aqueous particles deposited on a hydrophobically coated slide. A high-speed video camera was used to monitor AS efflorescence. The conclusion was that surface nucleation may occur in atmospheric particles. Experiments on homogeneous ice nucleation were performed also with nanometric droplets at temperatures below the homogeneous freezing limit established for micrometer sized water droplets (T = 235 K). Figure 4 shows ice nucleation rates as a function of temperature for nanometric droplets. The black line shows the rate calculated according to Huang and Bartell [58] , assuming that the solid-liquid interface increases as Tn, with n approximately 0.3. Manka et al. [28] reported homogeneous ice nucleation rates in nanometre size droplets (radii between 3.2 and
![]()
Figure 3. Nucleation rates vs. temperature in water-oil emulsions.
![]()
Figure 4. Ice nucleation rate vs. temperature.
5.8 nm) produced in a supersonic nozzle. The temperatures were between 202 K and 215 K (well within water’s “no man’s land”) and lower than those reported in the above papers (234 - 240 K). The authors report the nucleation rate for both purely volume and purely surface based processes, without addressing the problem of distinguishing between volume and surface nucleation, following the suggestion of Sigurbjörnsson and Signorell [59] . Actually, the reported data should suggest a prevalence of surface nucleation, as JS is three times higher for r = 3.2 nm droplets with respect to 5.8 nm, while JV is six times higher, instead of remaining constant. Assuming that nucleation occurs throughout the droplet volume, the measured ice nucleation rates JV are of the order of 1023 cm−3∙s−1 and are in agreement with the earlier work of Bartell and Chusak [60] in the region of overlap. At high temperatures (Figure 1), both the experimental and theoretical nucleation rates increase dramatically as the temperature decreases, while at the lower temperatures (Figure 4) the data of Manka et al. [28] and Bartell and Chusak [60] show that the ice nucleation rate is relatively insensitive to temperature.
4. Discussion
The surface and/or volume homogeneous nucleation of water droplets appears to be a questionable problem. Koop [61] , by comparing data on ice nucleation for liquid water droplets in gaseous environment based on surface and volume nucleation, concluded that “at present there is no conclusive evidence of a surface homogeneous ice nucleation in water or aqueous solution”. The droplets in the reported experiments were between 2 μm to 100 μm. We note, however, that the true data of Duft and Leisner [49] for surface nucleation (4.47 × 103 cm−2∙s−1, r = 49 μm; 1.81 × 103 cm−2∙s−1; r = 19 μm) are erroneously reported in Figure 15 of their paper. In addition, the reported data of Shaw and Lamb [53] concern freezing of droplets during evaporation not in stationary conditions, and in this case surface nucleation is favoured due to lower surface temperatures.
Sigurbjörnsson and Signorell [59] studied the freezing of nanosized aerosol particles, concluding that the experimental uncertainties and the approximation used for data evaluation make it impossible to distinguish between surface and volume nucleation mechanisms. However, considering the papers which deal with the problem of ice homogeneous nucleation, in our opinion there is prevalent agreement on the following statements: the contribution of surface nucleation increases by decreasing the radius of the supercooled droplets, and the surface (or sub-surface) nucleation rate is prevalent for droplets with radius lower than about 5 μm, in the temperature range between 235 - 240 K. In such cases, the atmospheric particles should freeze via propagation from the surface into the bulk, rather than propagating from the bulk to the surface. Therefore, the hypothesis of Tabazadeh et al. [29] appears plausible. In some cases surface nucleation was observed even with large droplets acoustically levitated [40] [50] , but in this case the sound intensity affects the nucleation process. Evidence in support of the assumption of Tabazadeh et al. [29] comes from computer simulations, that show a tendency for nucleation at or near the surface in fluid clusters. Molecular dynamics simulations have contributed to shed some doubt on the validity of classical nucleation theory.
Chushak and Bartell [62] and Chushak and Bartell [63] performed simulations of spontaneous phase transition in large, deeply supercooled clusters of SeF6. A striking result was that nucleation invariably occurred at or near the cluster’s surface, despite the fact that surfaces of clusters tend to be disordered and melt at significantly lower temperatures than their cores. Zasetsky et al. [64] performed molecular simulations to compare the local order in a thin film with the bulk liquid of supercooled water, and found that the probability of forming large clusters is much higher at (or close to) the interface than in the bulk water. The interface affects the nucleation kinetics and reduces the height of the free energy barrier, thus promoting the formation of nuclei. Turner and Bartell [65] employed molecular dynamic simulations to investigate the freezing of deeply supercooled liquid clusters of SeF6 and concluded that nucleation at or close to the surface is not uncommon, although the surface is certainly not the exclusive site. A clear trend overall for nucleation to occur closer to the surface with deeper supercooling was found.
Pluhařová et al. [66] studied homogeneous ice nucleation in neat and surface contaminated water by means of molecular dynamics simulations. In pure water nucleation preferentially started in the subsurface region. As models for the adsorbates, they assumed pentanol and pentanoic acid. The conclusion was that homogeneous ice nucleation is affected more by alcohol than by acid.
If homogeneous freezing initiates at the droplet surface, slight contamination by molecules within the surface layer, can hamper the rate of nucleation [67] . Studies have evidenced that organic aerosol (primary or secondary) can reduce the nucleation efficiency of supercooled droplets [68] [69] . If the surface is a preferential site for ice nucleation, the surface enrichment of supercooled cloud droplets by organic compounds could be the cause of this efficiency decrease. In the case of a volume nucleation, this influence should be smaller.
Therefore, anthropogenic emissions of organic compounds or precursors of organic compounds should have an effect on the composition and physical state of high-altitude clouds, and consequently on the radiative properties. Water surfaces are of special interest even in heterogeneous ice nucleation. For example, it has been observed that the an ice-forming nucleus tends to trigger the freezing of a supercooled water droplet at a higher temperature if it is placed close to the droplet surface, compared to when it is immersed in the droplet. Results indicate that when the ice nucleus is in contact with a droplet surface, the situation is more energetically favourable to nucleation than to immersion freezing [70] [71] .