The Prediction of Propagation Loss of FM Radio Station Using Artificial Neural Network ()
1. Introduction
In order to determine the propagation loss of an electromagnetic wave transmitted from one point to another or from one point to multiple points in most cases, it is important to understand how the RF propagation happens in outdoor environment.
As it is known, especially, the determination of propagation loss of radio waves in outdoor environment is too rigorous because of reflection, diffraction and scattering phenomena.
ITU-R 1546 method [1] , which is based on statistical measurement results, is frequently used to determine the propogation loss in VHF and UHF bands. The Figure 1 shows the change in electric field of a transmitter with effective radiated power 
with respect to distance and several antenna heights.
Epstein-Peterson is one of the major prediction models especially for irregular terrains, and it considers the effects of reflections on VHF and UHF bands [2] .
Besides the deterministic and empirical prediction models, Artificial Neural Networks (ANN) have been used lately as an alternative model. By using artificial neural networks, prediction of propagation loss in cellular systems has become possible [3] .
In this study, training the artificial neural network for a transmitter which broadcasts in 98.6 MHz FM band in
![]()
Figure 1. Electric field strength (dBµV/m) versus distance (km); the probability of location 50% and time 50% (f: 100 MHz, 1 kW erp).
Ankara, based on the measurement results acquired by considering only the topographic characteristics of the city is examined. The criteria of the transmitter which is used for the measurements are given in Table 1.
In mobile context, the measured power level can change depending on several parameters. (Multipath effect) Attenuation of the output power of a transmitter in the receiver’s site because of the distance and frequency is defined as the propagation loss.
2. Measurement Procedure
In order to study the prediction of propagation loss, a transmitter which broadcasts in FM band (88 - 108) MHz and with specific output power, antenna gain and antenna height values was utilized.
The frequency of the FM transmitter was determined as 98.6 MHz and the ERP (Effective Radiated Power) is as 44 dBW. For measuring the electromagnetic fields, the following equipment are used: an E-field measurement device (Audemat FM MC4), a monopole whip antenna, a geo-location finder (GPS) and lastly a laptop computer to be able to record measured results and location information together with them.
The measurements are gathered within the range starting from a point which is very close to transmitter and ending at location which is 25 kilometers away from it. The whip antenna was connected to the measurement device on the top of a vehicle and the location information was recorded automatically simultaneously.
Two different routes were chosen for the measurements. The first one is shown in Figure 2 and the other is shown in Figure 3. The measurement routes were plotted on Google Earth by using Mapinfo v.9 geographical information system (GIS).
![]()
Table 1. Transmitter and receiver parameters.
![]()
Figure 2. Measurement points (The first measurement route).
In order to train the artificial neural network, the input parameters were determined as 
(distance from transmitter),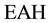 
(effective antenna height) and 
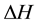(terrain irregularity factor).
For collecting further measurement values, those in the second route were considered. The measurement route is shown in the Figure 3.
3. Measurement Results
It is expected that the measurement loss will increase due to increasing the distance. The increasing of loss will occur because of the environmental factors (buildings, terrain conditions etc.) along with the free space loss. The Figure 4 shows how propagation loss changes with respect to distance. As shown in Figure 1, measurement values are collected up to a point which is 10 kilometers away from transmitter. The loss is 90 dB at a distance which is 1.5 kilometers away from the transmitter and increased to 120 dB on the 9th kilometer.
In the second route, many measurement values were collected. According to those, the measurement value is 90 dBµV/m on average on 1.5 kilometers away from the transmitter and decreased to 50 dBµV/m on the 26th kilometer (Figure 5).
4. Artificial Neural Network
Artificial neural networks are basically composed of input, hidden layers, output parameters and components which have ability to learn eventually by tuning the weight functions of the parametric model. They can mimic the learning function of human brain quite good.
Artificial neural network is an alternative to deterministic models for predicting propagation losses.
A neural network is defined as, consisting of simple processing unit in one piece parallel distributed processor [4] .
4.1. Neuron Model
The model with one output and several inputs is called Neuron Model. Figure 6 illustrates a simple neuron model. When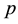 
is input parameter, w is weight value, 
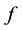is transfer function and a represents output value.
In an artificial neural network, there can be several input values. In this case, every input value is multiplied with weight parameter separately so that they can be trained until they reach a certain weight value, which means every input can have a different weight coefficient.
Figure 7 illustrates a model with several inputs. In this case the model looks like the following.
Mathematically, weights are added up with the bias values according to Equation (1).
![]()
Figure 4. Propagation Loss in the First Route.
![]()
Figure 5. Measurement values in the second route.
![]()
Figure 6. Single input and single output neuron model.
![]()
Figure 7. Multiple input and single output model.
![]()
(1)
The sigmoid function [5] is used which is defined as shown below Equation (2).
![]()
(2)
4.2. Levenberg-Marquardt Algorithm (Trainlm)
Levenberg-Marquardt algorithm is based on the method in which the training effort converges to its second derivative without calculating the Hessian matrix. When the performance function is equal to the sum of squares, Hessian matrix [6] is calculated as Equation (3),
![]()
(3)
and the gradient is![]()
. In those equations, ![]()
is the Jacobien matrix which involves the first derivatives of the network errors according to weights and biases and e is the network error vector. Jacobien matrix can be calculated by using the standard back-propagation technique.
Using the Newton-like approach, Levenberg-Marquardt algorithm transforms into Equation (4).
![]()
(4)
The ![]()
converges to zero, just as in Newton’s method. Moreover when ![]()
becomes a large number, it tr- ansforms into gradient which decreases gradually. Newton method provides more accurate and fast results and reduces errors to minimum.
4.3. Comparison between Experimental and Simulated Results
As a propagation model, Recommendation ITU 1546 was used along with Epstein-Peterson model. Coverage area of the transmitter is shown (Figure 8).
In the VHF band, the electromagnetic wave propagation in outdoor environment is modeled by the empirical methods as an alternative deterministic model. The neural network which is effective for modeling and characterization of complex systems has been developed for many applications [7] .
The measurement results were compared with those of the artificial neural network (Figure 9).
Piacentini and Rinaldi stated that the neural network is effective and safe in the estimation of propagation path loss [8] . ANN is used successfully in path loss prediction [9] . In the VHF band, ANN is used for estimating the electric field [10] . In the urban area, ANN is used for predicting the electric filed strength [11] .
ANN is much more efficient than the standard empirical model as well as it is operational as a theoretical model [12] .
As a result of the artificial neural network training, it was observed that the results of the prediction model are quite close to the measured values. Figure 10 clearly shows that the artificial neural network follows the fluctuations in the measured values.
The root mean squared error of prediction is, Equation (5).
![]()
(5)
where ![]()
represents measured value, while ![]()
![]()
represents theoretical value, ![]()
represents measurement number and ![]()
represents the error, which is RMSE = 9.57 dB (Table 2).
In real world, there are a lot of reasons for RMSE being higher than zero. In the urban area, it is very difficult to estimate electric field strength due to the scattering from buildings and cars. So it is almost near the RMSE value of 6 or 7 dB which are acceptable for estimation loss in the urban area.
The Levenberg-Marquardt network achieved best results in the comparison of the models.
In case of involving a Neural Model using Levenberg-Marquardt, the RMSE is lower than that of the classical model using Epstein-Peterson.
![]()
Figure 8. Coverage Area of the Transmitter (ERP = 44 dBW) by using ITU-1546 and Epstein-Peterson Model.
![]()
Figure 9. Measurement result versus artificial neural network results.
![]()
Figure 10. Results of the artificial neural network versus the measured values.
![]()
Table 2. The comparison of propagation model and ANN.
5. Results
ANN has become quite popular since the artificial neural networks made predictions in a less costly and in an easy manner.
In this paper, Levenberg-Marquardt algorithm which is a feed-forward propagation algorithm is implemented and run. The algorithm has produced very successful results in prediction of propagation loss. It can be clearly seen that artificial neural network provides more accurate results than those of the simulation. The study is based on three input parameters; distance, effective antenna height and ΔH, two hidden layers and one output (measurement value). The RMSE value obtained from an ANN is 9.57 whereas the RMSE value is found from prediction simulation 10.26.
From Figure 10, it can be clearly seen that the propagation prediction of electromagnetic waves by using the artificial neural network is more successful than the simulation based on Epstein-Peterson model and ITU-1546.
Finally, using more input parameters will possibly help train the artificial neural network better in order to produce more accurate results. Especially, clutter values of measured data and terrain clearance angle will make considerable contribution to the results when they are included among the input values. There are 20 - 30 dB differences between the measured values acquired in urban area and those acquired in the open area as they are measured in equal distances from the transmitter. Configuring the system according to those differences is considered as an important factor while training the artificial neural networks.
NOTES
*Corresponding author.