Thermodynamic Characteristics of Adsorption-Desorption of Methane in 3# Coal Seam of Sihe ()
1. Introduction
Coal methane mostly exists in the coal seams in the form of adsorption. Currently, the approach of coal methane desorption by drainage and lowering pressure for its ground production is widely adopted both at home and abroad. The method of negative pressure production with wells up and down connected is employed by Mine Gas Prevention and Control Center of Ningxia Bureau of Coal Geology at Shaqu Mine of Liulin County in Shanxi Province of China, and it has made great achievement with the production more than
10,000 m
3
per day. The new approach has shed light on the theory of methane production, and demands careful exploration of the nature of drainage and lowering pressure production. Through the experiments on methane adsorption-desorption isotherm [1] -[3] , by the calculations of isosteric heat of adsorption and maximum heat of adsorption with Clausius-Clapeyron equation, and by the contrast of the adsorption heat between methane and water vapor, the paper probes into the function and mechanism of water vapor in the process of water drainage and gas production.
2. Samples and Experimental Apparatus
Experimental samples are fresh raw coal collected by channel method from Sihe No. 3 coal (WY) in Shanxi Group of Permo-carboniferous system.
The collected samples, after being crushed, ground and screened, were processed into 60 - 80 mesh and made into moisture-equilibrated samples according to the standards of ASTM (American Society for Testing Material).
The experiments were accomplished by employing AST-2000 simulation experimental apparatus for bulk sample coalbed methane adsorption and desorption. The temperatures were set at 20˚C, 25˚C, 30˚C, 35˚C and 40˚C respectively.
3. Experimental Results
Figure 1 and Figure 2 are the isothermal adsorption-desorption data by making use of the fitting to simulate mathematics software of the moisture-equilibrated samples at different temperatures.
To express the action process of adsorption-desorption and pressure, the experimental data of adsorption at the five temperatures are
Langmuir
fitted [4] [5] , and the experimental data of desorption are descriptively fitted [6] [7] . The results are shown in Table 1, Figure 1 and Figure 2.
Langmuir
equation: 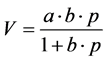
Desorption equation: 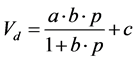
![]()
Figure 1. Fitted curves on experimental adsorption data by
Langmuir
equation of Sihe No. 3 WY.
![]()
Figure 2. Fitted curves on experimental desorption data of Sihe No. 3 WY.
![]()
Table 1. Fitted parameters of the experimental data at five temperatures.
4. Isosteric Heat of Adsorption
Isosteric heat of adsorption, also called differential heat of adsorption [8] , is the heat released as the infinitesimal methane molecules are adsorbed, with the adsorption capacity being constant. It is the enthalpy change [9] at the moment of adsorption.
Isosteric heat of adsorption is expressed as , calculated with Clausius-Clapeyron equation [10] [11] :
, calculated with Clausius-Clapeyron equation [10] [11] :
 (1)
(1)
In the equation: 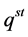 stands for isosteric heat of adsorption;
stands for isosteric heat of adsorption; 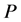 for pressure;
for pressure; 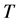 for absolute temperature;
for absolute temperature;  for gas constant, 8.314.
for gas constant, 8.314.
Integrate Equation (1) and get [12] :
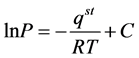 (2)
(2)
Calculation process: 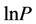 correlates with n, adsorption capacity; fit
correlates with n, adsorption capacity; fit 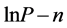 data and get
data and get 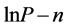 relation. Have several fixed
relation. Have several fixed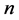 , and the corresponding lnP can be got with fitting formulas. Then, plot
, and the corresponding lnP can be got with fitting formulas. Then, plot ![]() with
with ![]() at fixed adsorption capacity and have linear fitting, so adsorption isostere is achieved, based on whose slope isosteric heat of adsorption is calculated.
at fixed adsorption capacity and have linear fitting, so adsorption isostere is achieved, based on whose slope isosteric heat of adsorption is calculated.
Calculation of isosteric heat of adsorption in process of adsorption of moisture-equilibrated samples of Sihe No. 3 WY.
1) Based on the experimental data of isosteric adsorption, draw a ![]() scatter diagram at different temperatures.
scatter diagram at different temperatures.
2) Have ![]() linear fitting, and the fitting equation is shown in Figure 3.
linear fitting, and the fitting equation is shown in Figure 3.
3) Based on the above fitting formula, calculate ![]() of
of![]() —fixed adsorption—
—fixed adsorption—![]() at different temperatures (20˚C - 40˚C), shown by Table 2.
at different temperatures (20˚C - 40˚C), shown by Table 2.
4) Plot ![]() data graph.
data graph.
5) At different fixed adsorption capacity, linearly fit the relational data of ![]() and
and![]() . The fitting equation is shown by Figure 4.
. The fitting equation is shown by Figure 4.
![]()
Figure 3. Relationship of pressures (logarithms) and adsorption capacity in the adsorption process.
![]()
Table 2. Calculations of lnP on different adsorption capacity in the adsorption process.
![]()
Figure 4. Isosteric adsorption line in the adsorption process.
6) Based on the slope of linear fitting, find isosteric heat of adsorption at different adsorption capacity by Equation (3).
![]() (3)
(3)
In the equation, ![]() is the slope of linear fitting equation.
is the slope of linear fitting equation.
The calculations are shown in Table 3.
7) Figure 5 is the curve of isosteric heat of adsorption with the change of adsorption capacity.
In the same way, calculate the isosteric heat of adsorption in process of desorption of moisture-equilibrated samples of Sihe No. 3 WY.
1) Based on the experimental data of isosteric desorption at different temperatures, Figure 6 is created by relating ![]() (KPa)—the natural logarithm of pressure to
(KPa)—the natural logarithm of pressure to ![]() (mmol/g)—adsorption capacity.
(mmol/g)—adsorption capacity.
2) Fit the data with linear lnP-n. The fitting equation is shown by Figure 6.
3) Based on the above fitting formula, calculate the value of ![]() on
on![]() —fixed adsorption —
—fixed adsorption —![]() at different temperatures (20˚C - 40˚C), shown by Table 4.
at different temperatures (20˚C - 40˚C), shown by Table 4.
4) Plot ![]() data graph.
data graph.
5) At different fixed adsorption capacity, linearly fit the relational data of ![]() and
and![]() . The fitting equation is shown by Figure 7.
. The fitting equation is shown by Figure 7.
6) Based on the slope of linear fitting, i.e.![]() , find isosteric heat of adsorption at different adsorption capacity by Equation (3). The results are shown by Table 5.
, find isosteric heat of adsorption at different adsorption capacity by Equation (3). The results are shown by Table 5.
7) Figure 8 is the curve of isosteric heat of adsorption with the change of adsorption capacity.
5. Maximum Heat of Adsorption
Maximum heat of adsorption is the isosteric heat of adsorption when the pressure tends to zero [13] [14] .
Usually Virial equation is used to calculate maximum heat of adsorption. In the condition of extremely low pressure, adsorption isotherm should conform to
Henry
Law [15] -
[17] :
![]() (4)
(4)
In the equation:![]() , adsorption capacity,
, adsorption capacity,![]() ;
;![]() , equilibrium pressure, KPa;
, equilibrium pressure, KPa;![]() ,
Henry
constant, mmol·g−1/KPa.
,
Henry
constant, mmol·g−1/KPa.
Virial Equation is used to describe the adsorption isotherm in the whole process of experimental scope, and by the way of extrapolation, ![]() ,
Henry
Law
constant, can be found when the pressure is towards zero in the low pressure area. Then,
,
Henry
Law
constant, can be found when the pressure is towards zero in the low pressure area. Then, ![]() , maximum heat of adsorption, can be found by Vant Hoff Equation which
, maximum heat of adsorption, can be found by Vant Hoff Equation which ![]()
![]()
Figure 5. Change of isosteric heat of adsorption with adsorption capacity in adsorption process of Sihe No. 3 WY.
![]()
Figure 6. Relationship of pressures (logarithms) and adsorption capacity in the desorption process.
![]()
Table 3. Calculations of the isosteric heat of adsorption in the adsorption process.
![]()
Figure 7. Isosteric adsorption line in the desorption process.
![]()
Figure 8. Isosteric heat of adsorption with adsorption capacity in desorption process of Sihe No. 3 WY.
![]()
Table 4. Calculations of lnP on different adsorption capacity in the desorption process.
![]()
Table 5. Calculations of the isosteric heat of adsorption in the desorption process.
and ![]() abide by. Vant Hoff Equation goes as follows:
abide by. Vant Hoff Equation goes as follows:
![]() (5)
(5)
In the equation, the physical interpretation of ![]() is the mole enthalpy difference between adsorption state and gas state when the pressure tends to zero, so
is the mole enthalpy difference between adsorption state and gas state when the pressure tends to zero, so ![]() is actually
is actually![]() , maximum heat of adsorption.
, maximum heat of adsorption.
Find
Henry
Law
constant ![]() [18] [19] by Virial Equation
[18] [19] by Virial Equation
Virial Equation below is used to describe adsorption isotherm when adsorption is in equilibrium.
![]() (6)
(6)
In the equation:![]() , two-dimensional dispersion pressure;
, two-dimensional dispersion pressure;![]() , Virial constant.
, Virial constant.
Equation (6) can be transformed by Gibbs Equation to Virial adsorption isotherm:
![]() (7)
(7)
When the pressure is very low, ![]() is relatively small, and high order term can be neglected. Then, the plotting of
is relatively small, and high order term can be neglected. Then, the plotting of ![]() to n should be linear. In other words,
Henry
Law
is tenable, so the value of
to n should be linear. In other words,
Henry
Law
is tenable, so the value of![]() ,
Henry
Law
constant, can be determined by the extrapolation value when
,
Henry
Law
constant, can be determined by the extrapolation value when![]() . From the above equation, when
. From the above equation, when![]() ,
,
![]() (8)
(8)
Therefore,
Henry
Law
constant![]() . In this condition, the following equation is found:
. In this condition, the following equation is found:
![]() (9)
(9)
Suppose the intersection value of plotting and vertical axis is![]() , and
, and![]() . Then,
. Then,
![]() (10)
(10)
Therefore,
Henry
constant ![]() can be found based on the result of fitting straight line in low pressure.
can be found based on the result of fitting straight line in low pressure.
The method of finding
Henry
constant ![]() by extrapolation is reliable because the experimental data in the low pressure area are linear, which guarantees the validity of
by extrapolation is reliable because the experimental data in the low pressure area are linear, which guarantees the validity of![]() . Therefore, the calculated value of
. Therefore, the calculated value of ![]() is also accurate.
is also accurate.
Calculation of maximum heat of adsorption by
Henry
constant
The relationship between the known
Henry
Law
constant ![]() and temperature abide by Vant Hoff Equation. If the interphase heat capacity difference is neglected, the result below can be got by integral:
and temperature abide by Vant Hoff Equation. If the interphase heat capacity difference is neglected, the result below can be got by integral:
![]() (11)
(11)
Usually the plotting of ![]() and
and ![]() is linear,
is linear, ![]() , maximum heat of adsorption, is determined by its slope.
, maximum heat of adsorption, is determined by its slope.
Calculation of maximum heat of adsorption in process of adsorption of moisture-equilibrated samples of Sihe No. 3 WY.
1) Based on the experimental data of isosteric adsorption at different temperatures, plot with Virial ![]() (KPa/mmol·g−1) and adsorption capacity
(KPa/mmol·g−1) and adsorption capacity ![]() (mol·g−1). (See Figure 9)
(mol·g−1). (See Figure 9)
2) Linearly fit Virial plotting by![]() . (See Table 6)
. (See Table 6)
3) Based on fitting result intercept, i.e. the value of![]() , calculate
Henry
Law
constant
, calculate
Henry
Law
constant ![]() by
by![]() . The results are shown in Table 7.
. The results are shown in Table 7.
4) Plot ![]() and
and ![]() and have linear fitting.
and have linear fitting.
![]() :
Vant
Hoff
plotting (See Figure 10)
:
Vant
Hoff
plotting (See Figure 10)
![]() : Linear fitting results:
: Linear fitting results:
![]()
5) Calculate maximum heat of adsorption based on![]() , the linear fitting slope. The equation is as follows:
, the linear fitting slope. The equation is as follows:
![]() (12)
(12)
![]()
Figure 9. Cross plotting with Virial for adsorption data of Sihe No. 3 WY.
![]()
Figure 10. Cross plot with
Vant
Hoff
for adsorption data of Sihe No. 3 WY.
![]()
Table 6. Fitted parameters of the Virial data in the adsorption process.
![]()
Table 7. Calculations of
Henry
Law
constant ![]() in the adsorption process.
in the adsorption process.
It is found![]() , the minus indicating that adsorption is an exothermic process.
, the minus indicating that adsorption is an exothermic process.
Calculation of maximum heat of adsorption in process of desorption of moisture-equilibrated samples of Sihe No. 3 WY.
1) Based on the experimental data of isosteric desorption at different temperatures, plot ![]() and
and![]() , adsorption capacity. (See Figure 11)
, adsorption capacity. (See Figure 11)
2) Fit Virial plotting by linear![]() . The results are shown in Table 8.
. The results are shown in Table 8.
3) Based on fitting result intercept, i.e. the value of![]() , calculate
Henry
Law
constant
, calculate
Henry
Law
constant ![]() by
by![]() . The results are shown in Table 9.
. The results are shown in Table 9.
4) Plot ![]() and
and ![]() and have linear fitting.
and have linear fitting.
![]() :
Vant
Hoff
plotting (See Figure 12)
:
Vant
Hoff
plotting (See Figure 12)
![]() : Linear fitting results:
: Linear fitting results:
![]()
5) Calculate maximum heat of adsorption based on![]() , the linear fitting slope.
, the linear fitting slope.
Find:![]() .
.
6. Contrast of Adsorption Heat Results
Table 10 is the isosteric heat of adsorption calculations result. The maximum heat of desorption process is higher than adsorption.
7. Conclusions
1) Adsorption heat and adsorption capacity are positively correlative.
2) Adsorption heat in rising pressure is less than that in dropping pressure. When the fixed adsorption capacity is 0.2 - 1.0 mmol/g, adsorption heat is 19 - 51 KJ/mol. Methane-coal adsorption belongs to physical adsorption [20] -[24] .
3) Desorption rate increases as the temperature rises. Adsorption heat in rising pressure is less than that in dropping pressure. To make desorption occur, heat supply is needed, and the adsorption heat of water vapor is larger than 40 KJ/mol. Therefore, as long as water vapor exists, desorption probably occurs in the system of methane-coal adsorption. We believe that pressure reduction results in the partial pressure increase of water va-
![]()
Figure 11. Cross plot with Virial for desorption data of Sihe No. 3 WY.
![]()
Figure 12. Cross plot with
Vant
Hoff
for desorption data of Sihe No. 3 WY.
![]()
Table 8. Fitted parameters of the Virial data in the desorption process.
![]()
Table 9. Calculations of henry law constant ![]() in the desorption process.
in the desorption process.
![]()
Table 10. Calculations of isosteric heat of adsorption.
por in the local space, and heat is released while water vapor adsorbs, and thus the methane molecules in the corresponding places of the pore surface turn into free state. In the methane-coal-water interface interaction, with micro-environmental pressure decreasing, methane’s desorption on the pore surface of coal is actually the result of replacement of methane molecules by water vapor (adsorption) in the corresponding adsorption sites.