On the Kenney-Lau Approach to Internal Stability Evaluation of Soils ()
1. Introduction
Normally, a soil comprises particles of different sizes. The relative amount by mass contributed by these particles defines the grain size distribution (i.e., grading) of the soil. A soil spread over a wide range of particle sizes is considered widely graded, whereas a grading containing few fractions is uniform. In a soil with stable grading, all particles contribute to the skeletal structure of the soil. In the case of unstable grading, there is an imbalance that creates a coarser fraction that is structural (with few highly stressed particle contacts) and a finer fraction, which is non-structural with moveable fine-grained particles (with no effective stress transfer between grains). Depending on the severity of seepage and the geometrical constraints of the coarser fraction of a grading, the finer fraction of the internally unstable soil can be washed out due to erosion by suffusion. Suffusion is a mechanism of internal erosion, which involves a “selective erosion of finer particles from the matrix of coarser particles (…) leaving behind a soil skeleton formed by the coarser particles” [1] . A soil subjected to suffusion may have its geotechnical properties changed and thus, in engineering practice, will become less effective in its intended function (e.g., filters in dams).
Stemming back to the filter rules of Terzaghi [2] , Kezdi and Sherard [3] [4] independently proposed theoretical methods to assess internal stability by splitting the grading into a fine part and a coarse part to evaluate the self-filtering ability of the soil. Subsequently, Kezdi [3] introduced the concept of suffusion as an erosion mechanism. However, from the viewpoint of the USACE [5] filter experiments, Kenney and Lau [6] - [8] significantly furthered the concept of internal stability by introducing their method for the shape analysis of gradings. Based on laboratory seepage tests on non-cohesive granular soils, they showed that, in addition to irregularly shaped gradings (such as those of gap-graded soils), evenly shaped gradings can be internally unstable too. In addition, Skempton and Brogan [9] confirmed the Kenney-Lau method with piping tests, which revealed that internally unstable grading seroded at significantly lower gradients than would be expected from the classical piping theory of Terzaghi.
Herein, the Kenney-Lau approach to the internal stability evaluation of soils is discussed. The tested gradings, the evolution of the boundary relation between internal stability and instability, and the laboratory results, which determine this boundary, are studied in detail in this paper. Furthermore, the Kenney-Lau approach has been adapted by others, and these extensions and potential improvements are discussed in addition to field experience comparisons from the application of the method in engineering practice.
2. Internal Stability of Soils
To Kenney and Lau [7] , grading stability refers to the ability of granular material to prevent the loss of its own small particles when subjected to disturbing forces such as seepage and vibration. For the unstable grading, as Kenney and Lau [7] continues, there is a primary fabric with moveable fine-grained particles in between its grains that are thus free to migrate into neighboring pores in a void network, and ultimately, the free fines will exit their initial material. However, smaller constrictions will hinder the migration of coarser particles, progressively reducing the size of the constriction due to blockage [7] . This parallels the self-filtering studies of Lafleur et al. [11] , which were undertaken during the same period of time.
Figure 1 shows different shapes of gradings, from uniformly shaped to widely graded with linear distributions and concave- and convex-shaped distributions. In the clast-supported structure where the coarser grains are structural (i.e., in grain-to-grain contact), with finer-grained particles either filling the voids of the coarser fraction or under-filling it, the soil may be internally unstable either due to gap-grading or due tothe fine soil particles passing through the constrictions of the coarser particles (Figure 1, i.e., curves b, 4 and 5). If all of the grains contribute to the stability of the clast-supported soil fabric, it is internally stable (Figure 1, i.e., curves a, 1 and 3). Conversely, the matrix-supported grading (Figure 1, i.e., curves 2 and c) has a coarser fraction without grain-to-grain contact, thus being predominately composed of a finer fraction, which contributes to transfer stresses with particles prevented from moving. The matrix-supported soil is not susceptible to internal instability induced erosion (i.e., suffusion). Internally unstable soils are typically those with concave- or gap-graded-shaped gradings [10] .
Thus, internal instability indicates on one aspect of internal erosion susceptibility of a soil, i.e., the geometrical constraints. The other aspect concerns hydraulic loading, i.e., the velocity of flow (i.e., critical gradient) through the soil matrix to cause movement of the finer fraction, and these criteria combined, i.e., internal instability and critical seepage velocity, may cause internal erosion by suffusion [1] .
3. The Kenney-Lau Approach
The Kenney-Lau approach involves a shape analysis of the grain size curve over a length of its finer part. The predominant filter constriction is one-quarter the size of the small particles making up the filter (i.e., D’c ≤ D5/4); thus, size D particles can pass through constrictions of filters composed of particles of size 4D and coarser [12] . In other words, a grain size distribution deficient in particles between size D and 4D is susceptible to the erosion of particles finer than D [7] .
The following rendition of the Kenney-Lau method reflects on the approach to internal stability evaluation of soils, and special emphasis is placed on the boundary relations between stable and unstable soils found by [6] - [8] and the soil specimens that were decisive in the choice of these boundaries.
![]()
![]()
Figure 1. Above are examples of shapes of gradings (after [5] ) (1: uniformly graded, 2: convex shaped, 3: straight lined, 4: gap-graded and 5: concave shaped) versus below, which shows principal soil compositions of gradings (adapted after [13] ) ((a) internally stable clast-supported soil, (b) internally unstable clast-supported soil and (c) matrix-supported soil).
3.1. Kenney-Lau Methodology
Kenney and Lau tested soil samples in permeameters with diameters of 245 and 580 mm and with a downward flow (Figure 2). The sample height varied from 200 to 245 mm in the 245-mm permeameter and from 380 to 550 mm in the 580-mm permeameter, and the sample diameters were 240 and 550 mm. A compressible layer of soft rubber liner was used to prevent the formation of preferential seepage channels along the inside wall of the permeameters [7] . Compaction by rodding (alternatively with a 100-mm diameter tamper) achieved a relative density of 100% in the 245-mm permeameter and approximately 80% in the 580-mm cell.
A drainage layer, sufficiently coarse to allow for an open system, was placed on the bottom of the cell against the samples. All samples were created from 10 to 20 individually mixed batches to ensure an overall grading uniformity. The test duration was at least 30 hours and until particles were no longer flushed out. In a companion study on controlling the constriction sizes of filters by Kenney et al. [12] , it was found that severe seepage conditions were required to move the largest possible particles though the constrictions of filters. The corresponding seepage flux was used by Kenney and Lau [7] , namely, a hydrodynamic number of R' ≥ 10, according to Equation (1), where q is a unit flux, D5 is the particle size at 5% mass passing, n is the porosity, and ν is the kinematic viscosity of water (approximately 10−6 m2/s). R' ≥ 10 is estimated for hydraulic gradients of approximately five to 60 [14] .
![]()
![]()
Figure 2. Laboratory setup with a 245-mm diameter seepage cell (left) and a 580-mm diameter cell (right) (after [7] ).
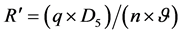 (1)
(1)
Vibration was added during testing by tapping the seepage cells with a rubber hammer. Subsequent to equilibrium, which was reached when insignificant amounts of solids were discharged [15] , the samples were removed in five to eight layers and sieved to determine the grain size distribution.
3.2. Tested Materials and Select Test Results
Kenney and Lau [6] - [8] tested, in total, 23 gradings (of which 18 are reproduced with their grain size distributions in Figure 3). The specimens “Cu = 3”, “Cu = 6” and “Cu = 12” are simply uniform, straight-lined gradings and are not shown in Figure 3 nor are specimens “20 A” and “21 A” because these are almost identical to “20” and “21”. Figure 4 and Figure 5 show the unstable and stable gradings separately.
3.2.1. Typical Behavior of Soils Tested as Unstable
The unstable soils usually exhibited three zones: a top transition zone with a coarse top surface, a central homogenous zone, and a bottom transition zone [7] . Compared to the initial grading, the diagnosis criterion was that any coarsening of the top transition zone proved the existence of loose movable particles; thus, the top layer’s grading indicates the primary fabric’s composition [6] . A change in the bottom layer was dependent on the drainage layer of the open system, thus being related to backward erosion and not to internal instability.
The homogenous central zone exhibited, in some cases, no net change from the initial grading (i.e., no loss of particles, or the same amount was lost as was gained during the test), and conversely, in other tests, this central zone had become coarser grained compared to the initial grading (i.e., a loss of particles throughout the sample).
3.2.2. Select Result—Unstable Specimen A and Borderline Stable Specimen As
Material A ranges from 0.2 to 40 mm (Figure 4), and although coarser, this material has a grading geometrically identical to the concrete sand mixture found to be unstable by USACE [5] , and in agreement, material A was also found to be internally unstable by Kenney and Lau [7] . The instability of material A, from the loss of finer particles, is illustrated by a comparison of the layer-wise gradings to the initial grading (Figure 6).The central homogenous zone (i.e., layers 3, 4 and 5), denoted as grading As in Figure 6, had lost particles finer than 2.5 mm (which corresponded to a 15% loss of mass). The bottom transition zone (i.e., layer 6) and the top transition zone (i.e., layer 1), as shown in Figure 6, are the coarsest most-washed-out layers exhibiting the composition of the primary fabric (i.e., the load-bearing grains).
The grading As had become stabilized in the test of grading A (i.e., part of the homogenous zone), and complementing tests were carried out on As, which revealed that the bottom layers (i.e., layers 5, 6 and 7) lost 9% of their mass and that the topmost layer 1 had become slightly coarser, indicating lost fines (Figure 6). Unexpectedly, however, the top layers 2 and 3 were unchanged in relation to the initial grading and formed a homogenous dense zone [6] [7] . Kenney and Lau [6] concluded that grading As was “close to being stable”, but it was reevaluated and found to be unstable [7] (i.e., the unchanged layers 2 and 3 were considered unintentional due to a fine-grained layer inlayer 3, which formed during compaction and that subsequently inhibited particle loss
![]()
Figure 3. Compiled grain size distribution curves of internally stable and unstable materials tested by Kenney and Lau (adapted after [7] [8] ).
![]()
Figure 4. Grain size distributions of internally unstable materials tested by Kenney and Lau (adapted after [7] [8] ).
from these layers). However, Sherard and Dunnigan [16] questioned this conclusion and tested a similar soil composition and found it to be stable. Kenney and Lau [8] retracted and instead concluded material As being stable. The unchanged top layer was considered the stable homogenous section, whereas the bottom coarser zone was evidence of a transition zone, not internal instability [8] . Material A and its stabilized composition in As became influential in the choice of boundary between stable and unstable gradings (further described in the following sections).
3.3. The Method and Its Boundary Relations
Kenney and Lau [7] estimated the maximum content of loose particles in a granular material to be equal to the primary fabric’s void space such that the total mass is determined according to Equation (2), where fp is the fraction of the primary fabric and fl is the fraction of loose particles.
 (2)
(2)
![]()
Figure 5. Grain size distributions of internally stable materials tested by Kenney and Lau (adapted after [7] [8] ).
![]()
![]()
Figure 6. Kenney-Lau test results for the unstable grading A (left) and the grading As, which was initially deemed unstable but was rebutted to being stable (after [7] ).
Furthermore, Kenny and Lau [7] expressed the primary fraction fp in terms of the void ratio of the primary fabric (i.e., ep) and the loose particle’s porosity (i.e., nl), and by using reasonable values of the primary fabric’s void ratio (ep ≈ 0.4) with the loose particle’s porosity (nl ≈ 0.4) in Equation (3), it was found that fp > 0.8 for widely graded material (Cu = D60/D10 > 3), which indicates that the content of loose material is at most 20% (30% for uniformly graded materials) [7] . A higher percentage of small particles indicates that these particles are not in a loose state but instead contribute to transfer stresses and are prevented from moving.
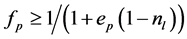 (3)
(3)
Given that the constrictions of a filter are one-quarter the size of the small particles making up the filter [12] , a deficiency in the grading between sizes D and 4D means that size D particles and finer can pass through the constrictions of the primary fabric, which is composed of particles of size 4D and coarser [7] . Thus, the Kenney-Lau method evaluates the potential for grading instability from the shape of the grain size curve in increments of four, namely, by determining if there is an insufficient amount of particles between D and 4D (i.e., denoted by H) in relation to the amount of mass passing at D (i.e., denoted by F). The boundary between stabilityand instability is H = F, but as discussed in the section below, the boundary evolved from a relation fitted against laboratory results to that of engineering relations for the optimum packing of soils.
The methodology of generating the H:F-shape curve and the extraction of the stability index (H/F)min (i.e., the smallest value along the H:F curve within the evaluation range, as first introduced by Skempton and Brogan [9] ) is given in Figure 7. The evaluation range for widely graded materials is the amount of mass passing being 0% to 20%, whereas uniformly graded is 0% to 30% [7] .
The Evolution of the Boundary Relations
The H:F-shape curves of the specimens tested by Kenney and Lau are shown in Figure 8, and the corresponding stability indexes are shown in Figure 9.
![]()
Figure 7. Description of the method of the Kenney-Lau approach for assessing the internal stability of filters, and the inset contains the H:F-shape curve and stability index (adapted after [7] [8] ).
![]()
Figure 8. H:F-shape curves of stable and unstable Kenney-Lau gradings against the boundary relations (adapted after [6] - [8] ).
![]()
Figure 9. Stability indexes (H/F)min of stable and unstable Kenney-Lau gradings against the boundary relations (adapted after [6] - [8] ).
Initially, a tentative boundary relation between stable and unstable gradings that equaled the H:F-shape curves of specimens tested as borderline stable, e.g., material Ys.s and As.s (particle size distributions in Figure 5) was proposed [6] . This boundary is denoted as H = FYs.s in Figure 10. To confirm its validity, materials with identical H:F curves were tested (i.e., materials 1 and 2 in Figure 8, which is flush with the boundary H = FYs.s), and these were found to be stable [6] .
However, the boundary was modified after studying the limiting grading curve of Loebotsjkov given in Equation (4) [7] , which expresses a curve with gradually finer particles fitting the constriction formed by a square array of four larger particles (a rendition of the Loebotsjkov curve is given in [6] ).
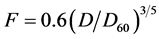 (4)
(4)
Adapting the Loebotsjkov curve to the H: F space, a logical linear relation of H/F = 1.3 is found (Figure 10), and this straight-line relation provides a good separation between stable and unstable shape curves, thus departing from the initial tentative boundary of H=FYs.s [7] . Material 3 (Figure 5, Figure 8 and Figure 9), with a grain size curve similar to Loebotsjkov’s curve, was tested and found to be stable, and its H:F-shape curve coincides with the H/F = 1.3 boundary, thus confirming its validity.
However, the H = 1.3F boundary was closely scrutinized [16] - [18] , and the results were challenged by the fact that materials that were otherwise entirely suitable in engineering practice would now be deemed unsuitable due to internal stability. Furthermore, Milligan [17] observed that the ideal gradation for the optimum density (i.e., the Fuller curve expressed by Equation (5)), which corresponds to a dense material whose voids are packed with gradually finer particles whereby the highest possible density is achieved, would be unstable. Logically, this is inconsistent with the idea that the internally unstable material has loose fines in the voids, and a material with Fuller-curve properties clearly does not.
![]() (5)
(5)
Although Kenney and Lau [8] interjected that density by itself is not a valid criterion to determine the hydraulic stability of granular soils, additional tests on Fuller-curve-shaped samples indeed confirmed that such a material is stable (plotted in Figure 5, Figure 8 and Figure 9 and denoted as material F). These aspects resulted in the abandonment of the boundary H = 1.3F in favor of Fuller’s curve (i.e., H = F in the H:F-space) (Figure 10). Nonetheless, Kenney and Lau [8] continued by saying “the inclination should be slightly reduced “to envelope all test data (i.e., specimens U and F). Such a boundary has the relation H = 0.9F (Figure 9 and Figure 10).
![]()
Figure 10. Evolution of Kenney-Lau boundaries between stable and unstable gradings (adapted after [6] - [8] ).
4. Discussion
4.1. Critical Gradient and Stress
Possibly the most influential work on the elaboration of the Kenney-Lau method is the research of Skempton and Brogan [9] , who introduced the stability index (i.e., (H/F)min from the minimum value along the Kenney-Lau H:F shape curve) and found from upward flow tests on sandy gravels that the critical hydraulic gradient for piping is linked to the stability index. In classical Terzaghi piping theory, the critical gradient ic in an upward flow should be approximately 1 in terms of sand fractions, but for the internally unstable sandy gravels, erosion initiated at gradients as low as one-fifth of the theoretical critical gradient [9] . This is explained by the contrast in stress imposed on the finer fraction versus the primary fabric; small pressures are exerted on sand particles, but the greater part of the overburden is exerted on the gravel particles [9] . A tentative relation between critical gradients and stability indexes was proposed by Skempton and Brogan [9] and is shown in Figure 11(a).
Li [19] found that the onset of instability in sand and gravels depended on the critical gradient and the effective stress (i.e., normalized mean vertical effective stress) and indirectly on the Kenney-Lau stability index (H/F)min, as shown in Figure 11(b). However, the failure modes were suffosion (i.e., mass movement, not simply free fines), which occurred in internally unstable materials, and heave, which occurred in internally stable materials. Nonetheless, the slopes of these hydromechanical gradient-effective stress envelopes agreed with the relative ranking of the stability index (H/F)min, meaning that higher stability indexes required higher critical gradients for the initiation of instability [19] .
4.2. Adaptations by Others
The Kenney-Lau method has been validated against tests of others in the literature, and adaptions have been made to potentially improve its predictive capacity [10] [19] [20] .
The comparative analysis of Li and Fannin [20] found that it may be useful to combine aspects of the Kenney- Lau method with the Kezdi criterion (as in [3] ); both methods examine the slope of the particle size distribution, and as reported by Li and Fannin [20] , the Kenney-Lau criterion is incremental over the grain size (which was found to be in good agreement for the amount of mass passing F < 15% but was shown to be conservative for higher values of F), whereas the Kezdi criterion is incremental over the percentage that is finer by mass (which was found to provide a better prediction forthe amount of mass passing F > 15%).
Wan and Fell [21] showed that combining the criteria of Burenkova (as in [22] ) and Kenney-Lau, i.e., eva-
![]()
![]() (a) (b)
(a) (b)
Figure 11. Internal stability relations: (a) critical gradient and stability index (H/F)min (after [9] ) and (b) critical gradient versus vertical effective stress (after [19] ).
luating the slope finer end of the grading (i.e., the Kenney-Lau approach) with the slope of the coarser fraction and the complete grain size curve (i.e., the Burenkova approach), improved the estimation of the internal stability of silt, sand and gravel mixtures.
Validity on Widely Graded Soils with Fines
The Kenney-Lau method is, strictly speaking, intended for granular non-cohesive materials, and widely graded soils with fines is outside of its scope. However, studies have been performed on its validity for widely graded soils with some fines [21] [23] - [25] .
In some cases, the Kenney-Lau method has been found to be conservative (i.e., over-predicting instability) (e.g., [10] [21] ); nonetheless, the Kenney-Lau method’s predictions were satisfactory when applied to coarse- grained soils with silt [23] [24] . Furthermore, when evaluating core gradings from the construction data of existing dams, Rönnqvist and Viklander [25] indicated that the Kenney-Lau method can be extended with caution to soils with fines provided the finer fraction (non-structural part of the grading) is less than 35% and provided the fines content (material finer than 0.075 mm) is less than approximately 30%.
The basis of the Kenney-Lau method is the evaluation of the finer end in increments of four, namely, the amount between D and 4D (i.e., denoted by H) in relation to the amount of mass passing at D (i.e., denoted by F). This is based on Kenney et al. [12] , who showed that a constriction of relatively uniform filters is one-quarter the size of the small particles making up the filter (i.e., D’c ≤ D5/4). However, tests on widely graded filters (i.e., Cu = D60/D10 of 20) indicate that these filters retain base particles approximately 1/2 the size of that of the uniform filter [26] , and in agreement, Kenney et al. [12] reported that filters with fractions finer than 0.2 mm appeared to have smaller constrictions than did fractions of coarser particles (although hydraulic transport conditions may have been insufficient to transport the largest possible particle). This suggests that the constrictions of widely graded, relatively fine-grained soils may be finer; thus, to better suit its properties, the normally used evaluation increment of four may need to be increased to a wider range (which will increase H) to reduce the potential for the over-prediction of internal instability. However, further work is necessary to develop the boundaries between stability and instability as well as the method’s evaluation range and increment range in terms of widely graded soils with fines.
4.3. Comparison to Field Experience
Empirical methods developed from laboratory studies may, in practice, have little systematic comparison to field experience, however, in terms of the Kenney-Lau method, comparison to engineering practice and the field has been done by e.g., Li et al. [23] and Rönnqvist [27] [28] .
Li et al. [23] evaluated construction data belonging to the core soil and transition component of an existing dam which suffered a sinkhole event in Canada, and given the sinkhole incident, they found that the Kenney- Lau method predicted successfully in view of the confirmed internal erosion occurrence. In a similar study, Rönnqvist [27] evaluated filter gradings with the objective to reinvestigate a sinkhole event in a Swedish dam; an assessment which also indicates that the Kenney-Lau method is successful in engineering practice.
On the large scale, Rönnqvist [28] compiled a database of 91 embankment dams with cores of glacial till that includes data on the core and filter zone of each dam. By use of performance monitoring data, 21 of the dams were identified as having a probable occurrence of internal erosion. A geo-statistical study of this population of dams indicated that Kenney-Lau method provided a satisfactory backtracking to the dams with probable occurrence of internal erosion, and the prediction became relatively more successful when combining the stability index of the filter with filter coarseness (i.e., filter D15).
5. Conclusions
The Kenney-Lau method determines the potential for internal instability in cohesion less granular soils. Relatively severe loading conditions were applied to the granular filter samples to promote the movement of the largest possible non-structural particles. Although there are reports that the method’s predictions may be overly conservative [10] [20] [21] , which may be associated with comparisons to test results from less severe hydraulic regimes without using vibrations, comparisons to field experience indicate satisfactory performance [23] [25] [27] . This paper has shown that an aspect that can influence the relative over-prediction of instability is that the postulated boundary between internal stability and instability (i.e., H = F) does not encompass all available Kenney-Lau data; some stable gradings are thus deemed unstable, which may incorporate a safety factor into the method.
The validity of the Kenney-Lau method for widely graded soils with some fines content needs further attention. Although it appears to have merit for coarse-grained soils containing some fines, especially in its Li-Fannin adaptation [23] [25] , further work is necessary to develop the boundaries between stability and instability as well as on the method’s evaluation range and increment range.
Acknowledgements
The research presented was carried out as part of the “Swedish Hydropower Centre-SVC”. SVC has been established by the Swedish Energy Agency, Elforsk and Svenska Kraftnät together with Luleå University of Technology, the Royal Institute of Technology, Chalmers University of Technology and Uppsala University.
The authors wish to acknowledge that financial support has also been received from WSP Sweden.
Notation
D, grain size (mm);
F, amount of mass passing at grain size D (%);
H, mass increment between D and 4D (%);
(H/F)min, stability index, defined by the smallest value of H/F, for 0% < F ≤ 20% in soil with a widely graded coarse fraction and 0% < F ≤ 30% in soils that are narrowly graded.