On Synchronization of Pinning-Controlled Networks with Reducible and Asymmetric Coupling Matrix ()
This paper investigates the synchronization of directed networks whose coupling matrices are reducible and asymmetrical by pinning-controlled schemes. A strong sufficient condition is obtained to guarantee that the synchronization of the kind of networks can be achieved. For the weakly connected network, a method is presented in detail to solve two challenging fundamental problems arising in pinning control of complex networks: 1) How many nodes should be pinned? 2) How large should the coupling strength be used in a fixed complex network to realize synchronization? Then, we show the answer to the question that why all the diagonal block matrices of Perron-Frobenius normal matrices should be pinned? Besides, we find out the relation between the Perron-Frobenius normal form of coupling matrix and the differences of two synchronization conditions for strongly connected networks and weakly connected ones with linear coupling configuration. Moreover, we propose adaptive feedback algorithms to make the coupling strength as small as possible. Finally, numerical simulations are given to verify our theoretical analysis.
1. Introduction
Complex dynamical networks are found to be common systems in our real world [1-6], such as genetic regulatory networks, biological neural networks, telephone graphs, etc. Therefore, lots of researchers from many fields of science and engineering are attracted to focus on analyzing their complex behaviors. Particularly, the synchronization of a complex network has received great interest and attention. In mathematical view, a concrete system can be modeled simply by a graph, where the nodes represent individuals of the networks and the edges stand for interactions between them. Therefore, Lyapunov stability theories and algebraic graph theories, as two essential tools, are used to study dynamic behaviors of the complex networks.
So far, as a basic and very useful kind of synchronization phenomenon, complete synchronization has been investigated widely [7-12]. For example, the authors studied the global synchronization for a collection of nonlinearly coupled chaotic systems with an asymmetrical coupling matrix in [7]. In [8], two profound problems were solved: one is how to choose suitable pinning schemes for a given complex network, the other is how large the coupling strength should be used in a complex network to achieve synchronization. Besides, [9] showed the number of node which should be pinned in a complex network in order to reach synchronization. It can be seen that in [13-17] that pinning adaptive method is very effective for solving synchronization of complex networks. In [16], the authors investigated the synchronization of nonlinearly coupled networks through an innovative local adaptive approach. By using the technique of pinning only a limited subset of the whole network, [17] showed that the complex network with coupled identical oscillators could be driven onto some desired common reference trajectory. Nowadays, more and more attentions are being paid to the optimization problems of pinning schemes [18-21]. For instance, the crucial problem that how to select an optimal combination between the number of pinned nodes and the feedback control gain is studied in [19].
However, the configuration coupling matrix is assumed to be symmetric and irreducible in most of previous literatures, which implies that the topology of the corresponding complex network is undirected and strongly connected. It is not consistent with the realistic world. For a strongly connected network, a single controller is enough to pin the network to the desired state. Whereas, in a weakly connected directed network, more than one nodes should be pinned to guarantee the network synchronization could be reached. Furthermore, the existent synchronization conditions usually require that the coupling strength must be large enough, which is not practical indeed. Thus, the interesting problem that how large coupling strength should be used for synchronization is raised. Until now, the fruitful results are rather few and sometimes it is hard to meet the requirement of practical operation.
In this paper, the constraints that the configuration coupling matrices are symmetric and irreducible are removed in order to overcome the aforementioned shortcomings arising from the constraints on the configuration coupling matrix. Instead, we assume the coupling matrix is asymmetric, weighted and reducible, which is more consistent with the realistic world, such as broadcasting. Moreover, the minimum number of pinned nodes and the quantity of coupling strength are obtained by an implicit inequality. And, an adaptive technique is adopted to make the coupling strength as small as possible.
The rest of this paper is organized as follows: In Section 2, some definitions, lemmas, hypotheses and basic models are proposed. In Section 3, based on Lyapunov stability theories, some criteria for the global and exponential synchronization in two cases are derived. The numerical simulations are given in Section 4, while some concluding remarks are displayed in Section 5.
We denote an n-order identity matrix by 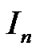 throughout this paper. The symmetric part of
throughout this paper. The symmetric part of
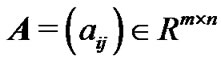 is shown as
is shown as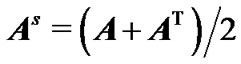 . Moreover,
. Moreover, 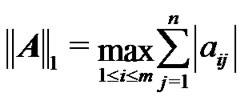 and
and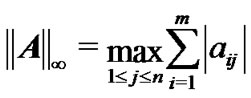 .
.
An n-order square matrix is positive definite denoted by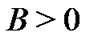 . If all eigenvalues of B are real, then we denote its
. If all eigenvalues of B are real, then we denote its 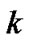 th largest eigenvalue as
th largest eigenvalue as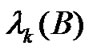 . At last, the notation
. At last, the notation  is Kronecker product.
is Kronecker product.
2. Preliminaries and Model Description
Consider a complex dynamical network consisting of 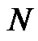 identical nodes with linearly diffusive coupling, which can be described by
identical nodes with linearly diffusive coupling, which can be described by

where 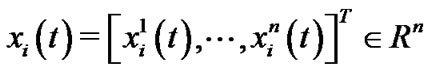 is the state variable of the
is the state variable of the 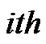 node,
node, 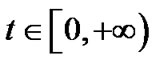 is the continuous time,
is the continuous time, 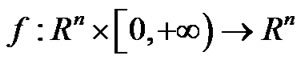 is a continuous map,
is a continuous map, 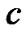 is the coupling strength, and
is the coupling strength, and 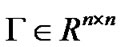 is the inner coupling matrix.
is the inner coupling matrix. 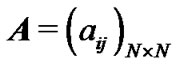 is the coupling configuration matrix representing the topological structure of the network, where
is the coupling configuration matrix representing the topological structure of the network, where 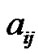 is defined as follows: if there exists a connection between node
is defined as follows: if there exists a connection between node 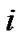 and node
and node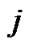 , then
, then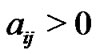 , otherwise,
, otherwise,
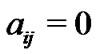 . Then the diagonal elements of matrix A are given by
. Then the diagonal elements of matrix A are given by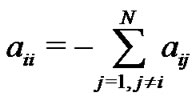 , which ensures the diffusion that
, which ensures the diffusion that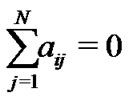 . Equivalentlynetwork (1) can be rewritten in a simpler form as follows:
. Equivalentlynetwork (1) can be rewritten in a simpler form as follows:

In this paper, we concentrate on the reducible coupling matrix A. Hence, we can assume that it has the following classic Perron-Frobenius normal form

where 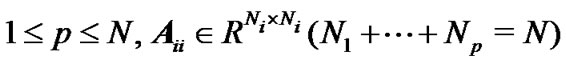 is either a scalar or a square and irreducible sub-matrix, and for any
is either a scalar or a square and irreducible sub-matrix, and for any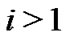 , there exists at least one j with
, there exists at least one j with 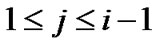 such that
such that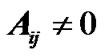 . It is equivalent to that the digraph has a directed spanning tree. Without loss of generality, we only discuss the case
. It is equivalent to that the digraph has a directed spanning tree. Without loss of generality, we only discuss the case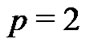 , that is
, that is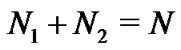 , and other cases can be dealt with similarly.
, and other cases can be dealt with similarly.
Corresponding to the Perron-Frobenius normal form of coupling matrix A, we can change the system (2) into the following form
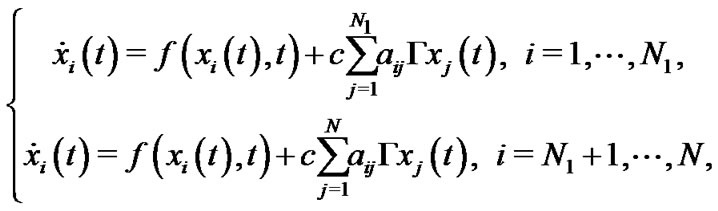 (3)
(3)
Then the synchronization of complex network model (3) is investigated. To realize the synchronization of network (3), some controllers will be added and the pinning controlled network can be described by
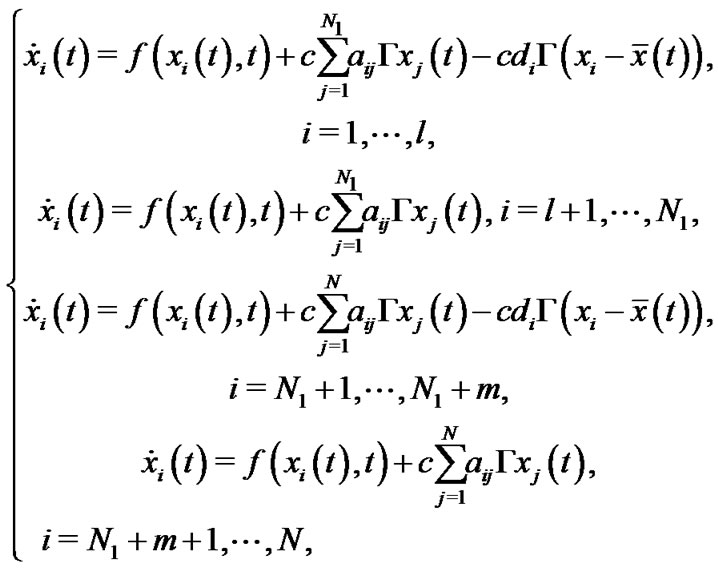 (4)
(4)
where 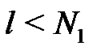 and
and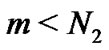 .
.
Denote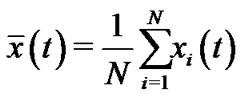 , and the error vectors are defined as
, and the error vectors are defined as 
Easily, we have that
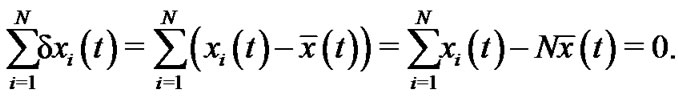 (5)
(5)
Notice that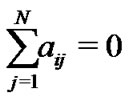 , then the error system can be described by
, then the error system can be described by
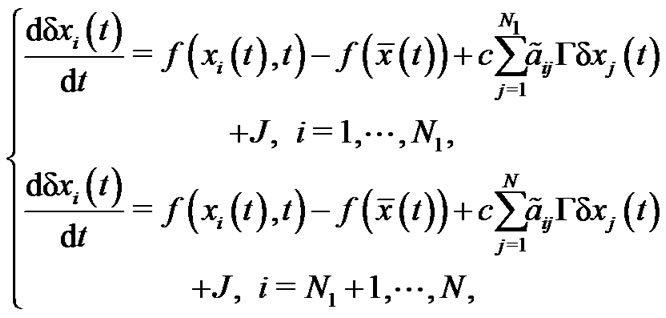 (6)
(6)
where 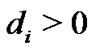 and
and

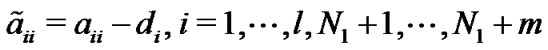 otherwise, and
otherwise, and

Assumption 1. [9]There exists a constant matrix K such that

for any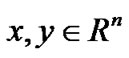 , where
, where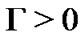 .
.
Note that Assumption 1 is very mild. For example, all linear and piecewise linear functions satisfy Assumption 1. In addition, if 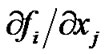
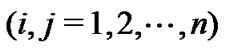 is bounded and
is bounded and 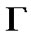 is positive definite, Assumption 1 is also satisfied. Therefore, it holds for many well-known systems, such as the Lorenz system, Chen system, L
is positive definite, Assumption 1 is also satisfied. Therefore, it holds for many well-known systems, such as the Lorenz system, Chen system, L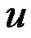 system, recurrent neural networks, Chua’s circuit, etc.
system, recurrent neural networks, Chua’s circuit, etc.
Lemma 1 [22]. Suppose A and B are positive definite Hermitian matrices. Then for each


Remark 1. Denote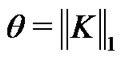 . According to Lemma 1, we have the following inequality
. According to Lemma 1, we have the following inequality

for any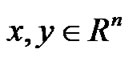 , which will be used repeatedly below.
, which will be used repeatedly below.
Lemma 2 [11]. If 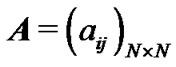 is an irreducible matrix that satisfies
is an irreducible matrix that satisfies 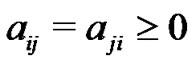 for
for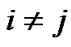 , and
, and 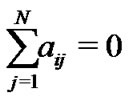 for all
for all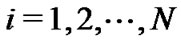 , then all eigenvalues of the matrix
, then all eigenvalues of the matrix

are negative, where 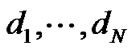 are nonnegative constants and
are nonnegative constants and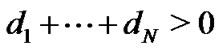 .
.
3. Main Results
In this section, some sufficient pinning criteria are derived to guarantee the globally asymptotical synchronization of complex dynamical networks.
In this subsection, we investigate the linearly coupled networks, where the coupling matrix is reducible and asymmetric.
Denote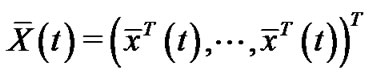 ,
,
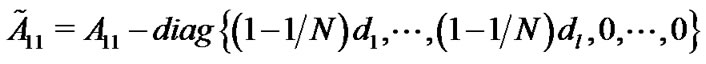 and
and

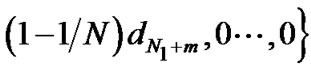 then we have the following theorem:
then we have the following theorem:
Theorem 1: Under the Assumption 1, if the following two inequalities
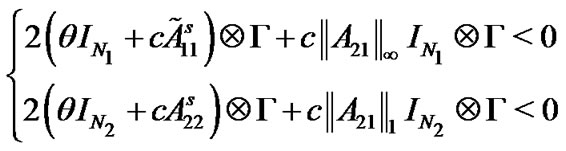 (8)
(8)
hold simultaneously, then the pinned network (4) can be globally asymptotically synchronized to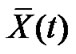 .Proof. Choose the Lyapunov function as
.Proof. Choose the Lyapunov function as


Denote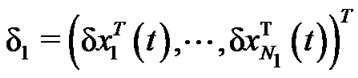 ,
,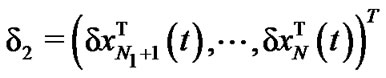 . From (7), we have
. From (7), we have






and








By Schwardz inequality, we can obtain


Therefore,






According to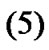 , we can obtain the following equality
, we can obtain the following equality

Combining with the above results, we have







Therefore, we can get 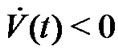 from (7). The proof is completed.
from (7). The proof is completed.
Obviously, the two conditions that 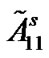 and
and 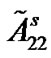 are negative are necessary for (8). Furthermore, we have to make the coupling strength c large enough, which meets the requirement of Theorem 1. Take
are negative are necessary for (8). Furthermore, we have to make the coupling strength c large enough, which meets the requirement of Theorem 1. Take 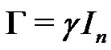 and
and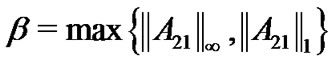 , where
, where 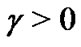 is a constant, then we can obtain the following results which are more applicable.
is a constant, then we can obtain the following results which are more applicable.
Corollary 1: The pinned network (4) can be globally asymptotically synchronized to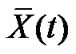 , when the following two inequalities
, when the following two inequalities
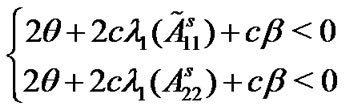 (9)
(9)
hold simultaneously.
The proof of Corollary 1 is obvious and is omitted here.
When the coupling strength c is large enough, if
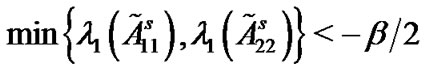 is satisfied, then it is easy for us to find that Corollary 1 holds. It happens that it provides us a direct way to compute that how many nodes should be pinned. Subsequently, we can obtain that the coupling strength c must be larger than
is satisfied, then it is easy for us to find that Corollary 1 holds. It happens that it provides us a direct way to compute that how many nodes should be pinned. Subsequently, we can obtain that the coupling strength c must be larger than

in order to reach synchronization. These results would be useful in pinning scheme by numerical simulations. Naturally, we can get the following corollary.
Corollary 2: Suppose that Assumption 1 holds and 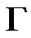 is positive definite. The pinned network (4) is globally synchronized if the coupling strength
is positive definite. The pinned network (4) is globally synchronized if the coupling strength 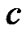 satisfies the following inequality
satisfies the following inequality

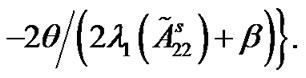 (10)
(10)
Denote

If the modified coupling matrix 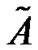 is irreducible, then it is easy to get the following corollary.
is irreducible, then it is easy to get the following corollary.
Corollary 3: Suppose Assumption 1 holds. The controlled network (4) can be globally synchronized to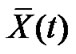 , provided the condition
, provided the condition 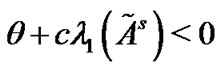 is satisfied.
is satisfied.
Proof. Take the Lyapunov function as

When the condition 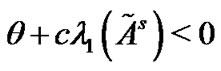 holds, by similar methods in Theorem 1, we can gain that
holds, by similar methods in Theorem 1, we can gain that 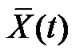 is globally asymptotically stable.
is globally asymptotically stable.
Remark 2: If Corollary 1 holds, then 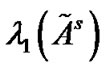 must be negative. Consequently, the synchronization of the controlled network can be realized as long as the coupling strength
must be negative. Consequently, the synchronization of the controlled network can be realized as long as the coupling strength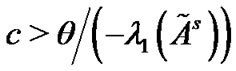 . Clearly, the smaller
. Clearly, the smaller
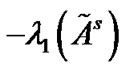 is, the larger the coupling strength has to be, which means we need spend more cost on achieving the synchronization of the pinned network. Then, it is nature to make
is, the larger the coupling strength has to be, which means we need spend more cost on achieving the synchronization of the pinned network. Then, it is nature to make 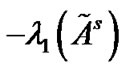 larger. By the Courant-Fischer Theorem, we can obtain the conclusion that
larger. By the Courant-Fischer Theorem, we can obtain the conclusion that 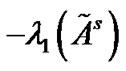 increases as the feedback control gains
increases as the feedback control gains 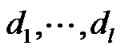 increase.
increase.
We conclude that the sufficient condition in Corollary 1 and the one in Corollary 3 could be compared formally. For the complex network which has a directed spanning tree, we must spend more cost on driving it to synchronize. And, it is coincident that this extra cost spent in the reducible network is caused by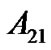 . It is reasonable and practical just because its corresponding strongly connected network possesses more links, such as the internet, the WWW net, which guarantees its synchronization can be reached with fewer external energy.
. It is reasonable and practical just because its corresponding strongly connected network possesses more links, such as the internet, the WWW net, which guarantees its synchronization can be reached with fewer external energy.
It is not difficult to find that the theoretical coupling strength given in (10) is too conservative. Usually, it is much larger than the needed value. Obviously, the intuitive idea is to make the coupling strength as small as possible. Here, the adaptive technique[23-24] is adopted to achieve this goal. The selected pinning controllers in (4), associated with the adaptive coupling law, lead to
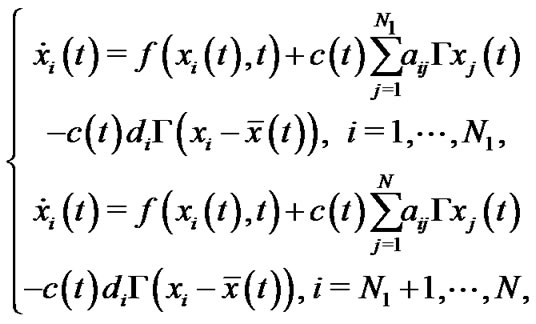 (11)
(11)
with
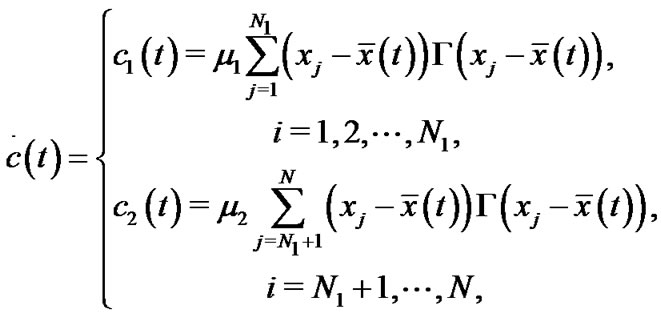 (12)
(12)
where 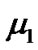 and
and 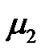 are small positive constants, and
are small positive constants, and

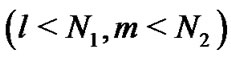 and
and 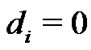 otherwise.
otherwise.
Define error vector as

and notice that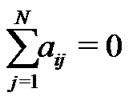 , then the error system of (11) can be described by
, then the error system of (11) can be described by
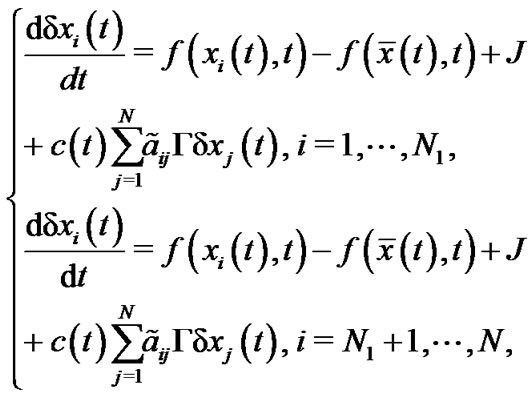 (13)
(13)
with
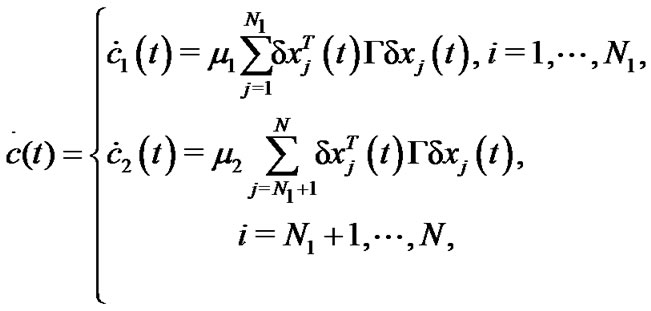 (14)
(14)
where
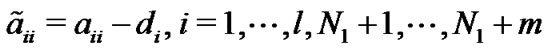 , and
, and 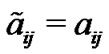 otherwise, and
otherwise, and

Theorem 2. Under Assumption 1, the adaptively controlled weakly connected network (11) with reducible and asymmetric coupling matrix can be globally synchronized for two small constants 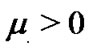 and
and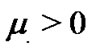 .
.
Proof. Consider the Lyapunov functional as follows:

Where


and 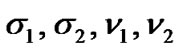 are positive constants to be determined below.
are positive constants to be determined below.
The derivative of 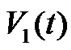 along the trajectories of (13) gives
along the trajectories of (13) gives







Similarly, the differential coefficient of 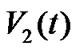 is described by
is described by




However, by some basic inequalities, we have


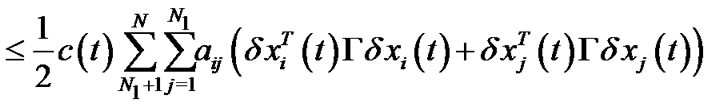 Therefore, we can obtain that
Therefore, we can obtain that




From Lemma 2, one can see that 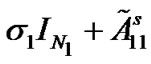 and
and 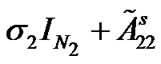 are negative definite when
are negative definite when 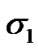 and
and 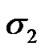 are sufficiently small. If we let the initial conditions
are sufficiently small. If we let the initial conditions 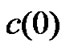 be large and
be large and 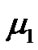 and
and 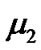 be small enough, then
be small enough, then 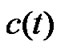 increase very slowly. In this case, if
increase very slowly. In this case, if 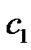 are given largely enough, then the synchronization can be achieved by Corollary 2. Once the synchronization is achieved,
are given largely enough, then the synchronization can be achieved by Corollary 2. Once the synchronization is achieved, 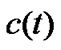 converge to two constants and is bounded. Since
converge to two constants and is bounded. Since 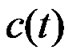 are bounded, we can always choose two sufficient large constants
are bounded, we can always choose two sufficient large constants 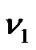 and
and 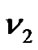 such that
such that

and

hold simultaneously, where
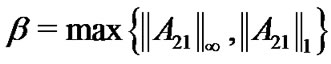 . Thus,
. Thus, 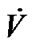 is always negative as time evolves. Hence, the pinned synchronization can be realized. And
is always negative as time evolves. Hence, the pinned synchronization can be realized. And 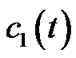 and
and 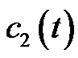 tend to constants respectively. Thus, the proof of Theorem 2 is completed.
tend to constants respectively. Thus, the proof of Theorem 2 is completed.
Remark 3: Notice that the synchronization conditions in Theorem 2 are independent of the network structure and the number of pinned nodes. Therefore, according to (12) by Theorem 2, under any fixed network structure and pinning controllers in the form of (6), the coupling strengths can be self-adaptively determined to achieve network synchronization.
4. Numerical Simulations
In this section, two simulation examples are given to verify the conclusions established above.
4.1 Validity of Theorem 1
In this numerical simulation, we consider a small-world network with 100 nodes. The connection weights are chosen randomly in 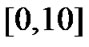 with uniform distribution. Here, we consider network (4) that consists of N identical Chen systems, where
with uniform distribution. Here, we consider network (4) that consists of N identical Chen systems, where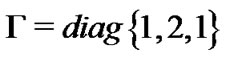 ,
, 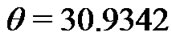 [7] and
[7] and

Define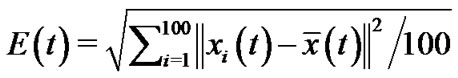 , which is used to measure the synchronization quality. Because the coupling matrices are produced randomly by matlab program, it needs many pinned nodes for attaining negative
, which is used to measure the synchronization quality. Because the coupling matrices are produced randomly by matlab program, it needs many pinned nodes for attaining negative 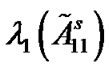 and
and 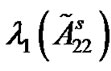 simultaneously. Hence, we choose five coupling matrices
simultaneously. Hence, we choose five coupling matrices 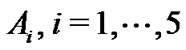 at random firstly. Then, take
at random firstly. Then, take
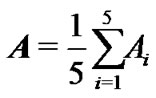 .
.
Let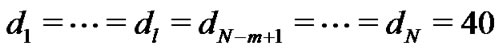 . Thus, we get
. Thus, we get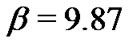 . If the combination of l and m make the inequality
. If the combination of l and m make the inequality 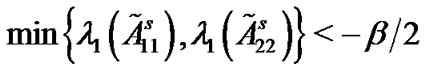 hold, then we say that the combination is valid. Moreover, we rule that
hold, then we say that the combination is valid. Moreover, we rule that 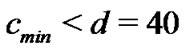 is acceptable. Table 1 reflects the valid relationships among l, m,
is acceptable. Table 1 reflects the valid relationships among l, m, 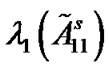 ,
, 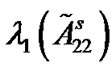 and the least threshold
and the least threshold 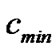 of coupling strength.
of coupling strength.

Table 1. Valid relationships among l, m, 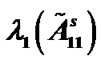 ,
, 
and the least threshold  of coupling strength.
of coupling strength.

Figure 1. The graph displays the synchronization process of the system (4).
According to the above two rules, 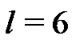 and
and 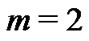 can meet our needs. Choose any initial values for
can meet our needs. Choose any initial values for 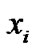 from
from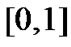 . Take
. Take 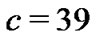 and
and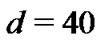 , then we can get the following synchronization graph Figure 1.
, then we can get the following synchronization graph Figure 1.
4.2. Verifying the Effectiveness of Theorem 2
In this simulation, all involved parameters are the same as those in Section 4.1 and the uncoupled chaotic system is still Chen system. And, we still use
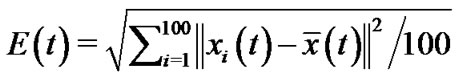 to reflect the synchronization quality. Then, we can obtain the following graph Figure 2, where the top one shows the synchronization process of the system (8) and the two ones in bottom display the limit process of
to reflect the synchronization quality. Then, we can obtain the following graph Figure 2, where the top one shows the synchronization process of the system (8) and the two ones in bottom display the limit process of 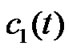 and
and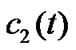 .
.
5. Conclusions
This paper considered the globally synchronization for a class of linearly coupled complex networks with reducible and asymmetrical coupling configuration. On

Figure 2. The graph displays the synchronization process of the system (10) and the limit process of 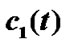 and
and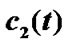 .
.
the basis of Assumption 1 and some lemmas, we obtained some theorems and corollaries by Lyapunov direct method which ensured the synchronization of pinned complex networks could be realized indeed. Moreover, by further analysis on the synchronization conditions in Theorem 1, one could obtain a detailed method for solving the two key problems in pinning synchronization: how many nodes should be pinned and how large coupling strength should be applied to realize the synchronization of pinned complex network. Moreover, it also revealed the relationships between the differences of two convergence conditions and the PerronFrobenius normal form of coupling matrix. At last, we provided two numerical simulations to verify the validity of those results.
6. Acknowledgements
The authors thank the referees and the editor for their valuable comments on this paper. The work is supported by the National Nature Science Foundation of P. R. China (Grant No. 10971159) and the Public Science and Technology Project of Shenzhen City (61001183).
[1] A. L. Barabási and R. Albert, “Emergence of Scaling in Random Networks,” Science, Vol. 286, No. 5439, 1999, pp. 509-512. doi:10.1126/science.286.5439.509
[2] S. H. Strogatz, “Exploring Complex Networks,” Nature, Vol. 410, 2001, pp. 268-276. doi:10.1038/35065725
[3] D. J. Watts and S. H. Strogatz, “Collective Dynamics of Small-World,” Nature, Vol. 393, 1998, pp. 440-442. doi:10.1038/30918
[4] S. A. Pandit and R. E. Amritkar, “Characterization and Control of Small-World Networks,” Physical Review E, Vol. 60, No. 2, 1999, pp. 1119-1122. doi:10.1103/PhysRevE.60.R1119
[5] Q. Song, J. D. Cao and W. W. Yu, “Second-Order LeaderFollowing Consensus of Nonlinear Multi-Agent Systems via Pinning Control,” Systems and Control Letters, Vol. 59, No. 9, 2010, pp. 553-562. doi:10.1016/j.sysconle.2010.06.016
[6] Q. Song and J. D. Cao, “On Pinning Synchronization of Directed and Undirected Complex Dynamical Networks,” IEEE Transactions on Circuit System I, Vol. 57, No. 3, 2010, pp. 672-680. doi:10.1109/TCSI.2009.2024971
[7] W. Lin and H. F. Ma, “Synchronization between Adaptively Coupled Systems with Discrete and Distributed TimeDelays,” IEEE Transactions on Automatic Control, Vol. 55, No. 4, 2010, pp. 819-830. doi:10.1109/TAC.2010.2041993
[8] X. W. Liu and T. P. Chen, “Synchronization Analysis for Nonlinearly-Coupled Complex Networks with an AsymMetrical Coupling Matrix,” Physica A, Vol. 387, No. 16- 17, 2008, pp. 4429-4439.
[9] W. W. Yu, G. R. Chen and J. H. Lü, “On Pinning SynChronization of Complex Dynamical Networks,” Automatica, Vol. 45, No. 2, 2009, pp. 429-435. doi:10.1016/j.automatica.2008.07.016
[10] Z. G. Zhang and X. Z. Liu, “Observer-Based Impulsive Chaotic Synchronization of Discrete-Time Switched Systems,” Nonlinear Dynamics, Vol. 62, No. 4, 2010, pp. 781-789. doi:10.1007/s11071-010-9762-y
[11] W. L. Guo, F. Austin and S. H. Chen, “Global Synchronization of Nonlinearly Coupled Complex Networks with Non-Delayed and Delayed Coupling,” Communications in Nonlinear Science and Numerical Simulation, Vol. 15, No. 6, 2010, pp. 1631-1639. doi:10.1016/j.cnsns.2009.06.016
[12] F. Liu, Q. Song and J. D. Cao, “Improvements and Application of Entrainment Control for Nonlinear Dynamical Systems,” Chaos, Vol. 18, No. 4, 2008, pp. 043120. doi:10.1063/1.3029670
[13] T. P. Chen, X. W. Liu and W. L. Lu, “Pinning Complex Networks by a Single Controller,” IEEE Transactions on Circuits and Systems-I: Regular Papers, Vol. 54, 2007, pp. 1317-1326. doi:10.1109/TCSI.2007.895383
[14] W. G. Xia and J. D. Cao, “Pinning Synchronization of Delayed Dynamical Networks via Periodically Intermittent Control,” Chaos, Vol. 19, No. 1, 2009, Article ID: 013120.doi:10.1063/1.3071933
[15] D. P. Lellis, D. M. Bernardo and F. Garofalo, “Synchronization of Complex Networks through Local Adaptive Coupling,” Chaos, Vol. 18, No. 3, 2008, Article ID: 037110.doi:10.1063/1.2944236
[16] D. P. Lellis, D. M. Bernardo and F. Garofalo, “Novel Decentralized Adaptive Strategeis for the Synchronization of Complex Networks,” Automatica, Vol. 45, No. 5, 2009, pp. 1312-1318. doi:10.1016/j.automatica.2009.01.001
[17] M. Porfiri and D. M. Bernardo, “Criteria for Global PinningControllability of Complex Networks,” Automatica, Vol. 44, No. 12, 2008, pp. 3100-3106.
[18] T. Yanagita and A. S. Mikhailov, “Design of Easily Synchronizable Oscillator Networks Using the Monte Carlo Optimization Method,” Physical Review E, Vol. 81, No. 5, 2010, Article ID: 056204. doi:10.1103/PhysRevE.81.056204
[19] J. C. Zhao, J. A. Lu and X. Q. Wu, “Pinning Control of General Complex Dynamical Networks with Optimization,” Science China-Information Sciences, Vol. 53, No. 4, 2010, pp. 813-822. doi:10.1007/s11432-010-0039-3
[20] G. S. Duane, “A ‘Cellular Neuronal’ Approach to Optimization Problems,” Chaos, Vol. 19, No. 3, 2009, Article ID: 033114.doi:10.1063/1.3184829
[21] J. H. Park, S. M. Lee and H. Y. Jung, “LMI Optimization Approach to Synchronization of Stochastic Delayed DiscreteTime Complex Networks,” Journal of Optimization Theory and Application, Vol. 143, No. 2, 2009, pp. 357-367. doi:10.1007/s10957-009-9562-z
[22] L. Z. Lu and C. E. M. Pearce, “Some New Bounds for Singular Values and Eigenvalues of Matrix Product,” Annals of Operations Research, Vol. 98, No. 1-4, 2000, pp. 141-148. doi:10.1023/A:1019200322441
[23] W. W. Yu, J. D. Cao, K. W. Wong and J. H. Lü, “New Communication Schemes Based on Adaptive SynchroniZation,” Chaos, Vol. 17, No. 3, 2007, Article ID: 033114. doi:10.1063/1.2767407
[24] X. F. Li, A. C. S. Leung and X. P. Han, “Complete (Anti-) Synchronization of Chaotic Systems with Fully Uncertain Parameters by Adaptive Control,” Nonlinear Dynamics, Vol. 63, No. 1-2, 2011, pp. 263-275. doi:10.1007/s11071-010-9802-7