Consideration on the Flow Velocity in the Experimental Analysis of the Flame Displacement Speed Using DNS Data of Turbulent Premixed Flames with Different Lewis Numbers ()
1. Introduction
Turbulent flames are the configuration to have been widely used for actual combustors for automobiles, ships, aircraft, power generations, and industrial furnaces. To achieve further high efficiency and low emission of the actual combustors, it is necessary to investigate the detailed mechanism of turbulent combustion. Burning velocity is one of the major characteristics in turbulent premixed flames. In the various definitions of the burning velocity, turbulent burning velocity is a global quantity and is related to combustion efficiency, while the local burning velocity and the flame displacement speed are the dominant factors in the discussion of the local structure of turbulent premixed flames. The local burning velocity is the quantity based on the local consumption rate of the unburned mixture by the chemical reaction, while the flame displacement speed is the quantity based on the flame normal component of the speed, which a flame surface, defined as the isosurface of temperature or mass fraction of the unburned mixture, moves relatively to a flow [1] . It is not straightforward to measure the local chemical reaction rate using the current measurement technology, thus the local burning velocity can be obtained numerically only. Therefore, the flame displacement speed has been used for experiments instead of the local burning velocity. The flame displacement speed is experimentally obtained from the displacement normal to the flame surface, while it is numerically evaluated by the transport equation of the flame surface which is defined as the isosurface of the reaction progress variable. These flame displacement speeds obtained both experimentally and numerically cannot be compared directly because their definitions are different. Thus, it is necessary to investigate the relationship between the experimental and the numerical flame displacement speeds. The flame displacement speed involves flow velocity. In this relationship, the consideration of the flow velocity in the experimental flame displacement speed is also important.
Hartung et al. [2] developed the new experimental analysis and formulation of the flame displacement speed in turbulent premixed flames using stereoscopic particle image velocimetry (PIV) and time-sequenced OH-pla- nar laser-induced fluorescence (PLIF). The two-dimensional flame displacement speed was measured as the projection of the three-dimensional flame displacement speed onto the plane defined by the laser sheets intersecting a flame. Chakraborty et al. [3] performed the DNS analysis on the flame displacement speed using the experimental definition of the two-dimensional flame displacement speed by Hartung et al. [2] . The flame displacement speed is essentially a three-dimensional quantity. Because it is difficult to measure the three-dimen- sional flame displacement speed experimentally, the flame displacement speed is measured as a two-dimen- sional quantity. They evaluated the correlation between the two-dimensional flame displacement speed, which was obtained from the experimental formulation by Hartung et al. [2] , and the three-dimensional flame displacement speed, which was evaluated by the transport equation. They reported that the correlation was positive.
In our previous study [4] , the experimental measurement and analysis on the two-dimensional flame displacement speed were simulated and analyzed using the DNS data with the different density ratios of the unburned mixture to the burned product. In the simulated analysis on the experimental flame displacement speed, the treatment of the local flow on the flame surface was discussed, and it was found that the correlation between the experimental and numerical flame displacement speeds was affected by the density ratio and the isosurface of the reaction progress variable due to the dilation effect of the flame.
In this study, the experimental measurement and analysis on the two-dimensional flame displacement speed were simulated using the DNS data with the different Lewis numbers. The two-dimensional flame displacement speed obtained with simulating the experimental measurement and analysis was compared with the two-dimen- sional flame displacement speed numerically evaluated by the transport equation, and subsequently the correlation between the both flame displacement speeds was shown. In the simulation of the experimental measurement and analysis, the flow velocity involved in the simulated experimental flame displacement speed was considered as the mean flow or the local flow, and the impact of their flows on the correlation between the simulated experimental and the numerical flame displacement speeds was also shown. The experimental measurement and analysis on the flame displacement speed were assessed on the basis of the results simulated them using the DNS data.
2. Numerical Analysis Method
2.1. DNS Database
The DNS database used for the numerical simulated analysis of the experimental measurement and analysis was constructed with different Lewis numbers. These were Le = 0.8, termed case Ml; Le = 1.0, termed case Mm; and Le = 1.2, termed case Mh. The simulations were carried out using the PRIMEPOWER HPC2500 installed at Nagoya University [5] . Details of the database are given in Table 1, and the computational domain is shown in Figure 1. The governing equations for constructing the database were the conservation of mass, chemical species, energy, and momentum (compressible Navier-Stokes equations), and the equation of state for an ideal gas. The database was constructed using a sixth-order central finite difference scheme in the mean flow direction and a spectral collocation method in the directions perpendicular to the mean flow for spatial discretization. A third- order three-step Runge-Kutta method was used for the time evolution and an overall single-step irreversible reaction was used to describe the chemical kinetics. The inflow and outflow boundaries were described on the basis of Navier-Stokes characteristic boundary conditions (NSCBC) [6] [7] , and the lateral boundaries were periodic. The computational domain was 8 mm in the mean flow direction and 4 mm in the directions perpendicular to the mean flow; 512 and 128 grid points were used in the respective directions. At the inflow boundary, preliminary calculated homogeneous isotropic turbulence with a cycle of several milliseconds was used, with a mean inflow velocity assuming Taylor’s hypothesis of frozen turbulence with a phase shift. Initially, a laminar premixed flame was formed, which grew to form a turbulent premixed flame. The inflow velocity of the unburned mixture was adjusted while monitoring the turbulent burning velocity until the turbulent premixed flame became fully developed and stabilised. The instantaneous turbulent burning velocity varied temporally; however, the time-averaged turbulent burning velocity, which can be measured experimentally, was steady. The database was constructed without changing the inflow velocity. Each case in the database consisted of almost 200 sampled data points at 51.68-μs intervals (which was longer than the DNS time step). The conditions described in the database correspond to the boundary between wrinkled flamelets and corrugated flamelets in the turbulent combustion regime diagram [8] . Further details of the calculation method to construct the DNS database can be found in Nishiki et al. [9] [10] and Nishiki [11] .
2.2. Numerical Analysis Simulating Experimental Measurement
In this study, the DNS analysis simulated the experimental measurement and analysis of the flame displacement speed was performed in accordance with Renou et al. [12] [13] . The flame surface is experimentally measured as the two-dimensional cross section of a flame on a laser sheet using laser tomography. The analysis in this study was performed by simulating the experimental measurement and analysis using the data on the two-di- mensional cross section parallel to the mean propagation direction of a flame in the three-dimensional DNS data of turbulent premixed combustion. The flame surface was identified as the isosurface of the reaction progress variable:
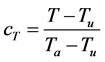 , (1)
, (1)
where T is the temperature, 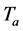 is the adiabatic flame temperature, and
is the adiabatic flame temperature, and 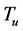 is the temperature of the unburned mixture (300 K). Three isosurfaces of the reaction progress variable in all the cases were considered as follows:
is the temperature of the unburned mixture (300 K). Three isosurfaces of the reaction progress variable in all the cases were considered as follows: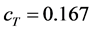 , the isosurface corresponding to 500 K where silicon oil droplets seeded in the unburned mixture evaporate [12] [13] ;
, the isosurface corresponding to 500 K where silicon oil droplets seeded in the unburned mixture evaporate [12] [13] ; , the isosurface where the temperature gradient indicates a maximum value;
, the isosurface where the temperature gradient indicates a maximum value;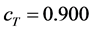 , the isosurface where the reaction rate in the planar flame reaches a maximum value. Two-dimen- sional flame displacement speed simulating the experimental measurement and analysis was defined by two kinds of equations dependent on the treatment of the flow velocity involving in the flame displacement speed:
, the isosurface where the reaction rate in the planar flame reaches a maximum value. Two-dimen- sional flame displacement speed simulating the experimental measurement and analysis was defined by two kinds of equations dependent on the treatment of the flow velocity involving in the flame displacement speed: 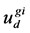 using the mean inflow velocity on the upstream boundary as shown in Figure 2(a),
using the mean inflow velocity on the upstream boundary as shown in Figure 2(a),
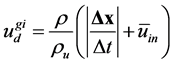 ; (2)
; (2)
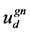 using the local flow velocity defined as the normal component of the local flow velocity at each point on the flame surface as shown in Figure 2(b),
using the local flow velocity defined as the normal component of the local flow velocity at each point on the flame surface as shown in Figure 2(b),
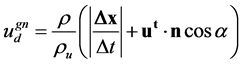 , (3)
, (3)
where 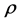 is the density,
is the density,  is the density of the unburned mixture,
is the density of the unburned mixture,  is the displacement vector of a flame,
is the displacement vector of a flame,  is the time interval of measurement,
is the time interval of measurement, ![]() is the mean inflow velocity,
is the mean inflow velocity, ![]() is the flow velocity vector at the time, t, and
is the flow velocity vector at the time, t, and ![]() is the angle between u and unit normal vector to a flame surface, n. The flame surfaces were measured experimentally every 0.167 ms in Renou et al. [12] [13] , whereas the DNS data were sampled every 0.0517 ms. For the similar simulating analysis using the DNS data to the experimental measurement and analysis in Renou et al. [12] [13] ,
is the angle between u and unit normal vector to a flame surface, n. The flame surfaces were measured experimentally every 0.167 ms in Renou et al. [12] [13] , whereas the DNS data were sampled every 0.0517 ms. For the similar simulating analysis using the DNS data to the experimental measurement and analysis in Renou et al. [12] [13] , ![]() was 0.1551 ms as three times of the interval sampled the DNS data. The two- dimensional flame displacement speed evaluated by the transport equation of
was 0.1551 ms as three times of the interval sampled the DNS data. The two- dimensional flame displacement speed evaluated by the transport equation of![]() ,
,
![]() (4)
(4)
![]() (a) (b)
(a) (b)
Figure 2. Schematic of simulating experimental analyses on the flame displacement speed. (a) ![]() obtained in consideration of the mean inflow velocity on the upstream boundary, (b)
obtained in consideration of the mean inflow velocity on the upstream boundary, (b) ![]() obtained in consideration of the normal component of the local flow velocity.
obtained in consideration of the normal component of the local flow velocity.
is defined as:
![]() . (5)
. (5)
Note that![]() ,
, ![]() , and
, and ![]() were non-dimensionalised by the laminar burning velocity without flame stretch in each case after the next section.
were non-dimensionalised by the laminar burning velocity without flame stretch in each case after the next section.
3. Results and Discussion
3.1. Flame Displacement Speed Involving the Mean Inflow Velocity
The probability density functions (pdfs) of both ![]() as the simulated experimental flame displacement speed involving the mean inflow velocity and
as the simulated experimental flame displacement speed involving the mean inflow velocity and ![]() evaluated by the transport equation on each isosurface of
evaluated by the transport equation on each isosurface of ![]() in the different Lewis number cases are shown in Figure 3. In all Lewis number cases, the pdfs of
in the different Lewis number cases are shown in Figure 3. In all Lewis number cases, the pdfs of ![]() disagreed with those of
disagreed with those of![]() . In each Lewis number case, however, the difference of the mode location between
. In each Lewis number case, however, the difference of the mode location between ![]() and
and ![]() decreased with
decreased with![]() , and the mode locations of both
, and the mode locations of both ![]() and
and ![]() were very close especially in
were very close especially in![]() .
. ![]() becomes larger in average in the downstream direction and smaller in average in the upstream direction. The flow velocity on the isosurface of
becomes larger in average in the downstream direction and smaller in average in the upstream direction. The flow velocity on the isosurface of ![]() where is less affected by the flame than the isosurfaces of
where is less affected by the flame than the isosurfaces of![]() , 0.900 is close to the mean inflow velocity on the upstream boundary. Therefore, the pdf of
, 0.900 is close to the mean inflow velocity on the upstream boundary. Therefore, the pdf of ![]() involving the mean inflow velocity was similar to the pdf of
involving the mean inflow velocity was similar to the pdf of ![]() involving the local flow velocity in the isosurface of
involving the local flow velocity in the isosurface of![]() . The joint pdfs of
. The joint pdfs of ![]() with
with ![]() on each isosurface of
on each isosurface of ![]() in the different Lewis number cases are shown in Figure 4. The joint pdfs of
in the different Lewis number cases are shown in Figure 4. The joint pdfs of ![]() with
with ![]() in the isosurface of
in the isosurface of ![]() had the largest probability density of the mode in the isosurfaces of
had the largest probability density of the mode in the isosurfaces of ![]() in each Lewis number case. However, the joint pdf of
in each Lewis number case. However, the joint pdf of ![]() with
with ![]() had almost no correlation in all cases. The correlation coefficients of
had almost no correlation in all cases. The correlation coefficients of ![]() with
with ![]() on each isosurface of
on each isosurface of ![]() in the different Lewis number cases are shown in Figure 5. The correlation coefficients were low values in all cases, even the largest coefficient on the isosurface of
in the different Lewis number cases are shown in Figure 5. The correlation coefficients were low values in all cases, even the largest coefficient on the isosurface of ![]() in case Mh did not reach 0.3. This implies that the mean inflow velocity is not appropriate to the flow velocity involved in the flame displacement speed.
in case Mh did not reach 0.3. This implies that the mean inflow velocity is not appropriate to the flow velocity involved in the flame displacement speed.
3.2. Flame Displacement Speed Involving the Local Flow Velocity
The pdfs of both ![]() as the simulated experimental flame displacement speed involving the normal component of the local flow velocity at each point on the flame surface and
as the simulated experimental flame displacement speed involving the normal component of the local flow velocity at each point on the flame surface and ![]() in the different Lewis number cases are shown in Figure 6. The mode locations of
in the different Lewis number cases are shown in Figure 6. The mode locations of ![]() and
and ![]() in each isosurface of
in each isosurface of ![]() were almost constant independent of the Lewis number. The shapes and the mode locations of the pdfs of
were almost constant independent of the Lewis number. The shapes and the mode locations of the pdfs of ![]() in the isosurface of
in the isosurface of ![]() were similar to those of
were similar to those of ![]() in case Mm, Mh. This indicates the possibility that
in case Mm, Mh. This indicates the possibility that ![]() is more appropriate definition of the experimental flame displacement speed than
is more appropriate definition of the experimental flame displacement speed than![]() . The joint pdfs of
. The joint pdfs of ![]() with
with ![]() on
on
![]()
Figure 3. Probability density functions (pdfs) of non-dimensionalised ![]() and
and ![]() on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
![]()
Figure 4. Joint pdfs between non-dimensionalised ![]() and
and ![]() on some isosurfaces of cT with different Lewis numbers. From the top, case Ml, case Mm, and case Mh, and from the left, cT = 0.167, 0.690, 0900.
on some isosurfaces of cT with different Lewis numbers. From the top, case Ml, case Mm, and case Mh, and from the left, cT = 0.167, 0.690, 0900.
![]()
Figure 5. Correlation coefficients between non-dimensionalised ![]() and
and ![]() on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
![]()
Figure 6. Pdfs of non-dimensionalised ![]() and
and ![]() on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
each isosurface of ![]() in the different Lewis number cases are shown in Figure 7. The joint pdfs of
in the different Lewis number cases are shown in Figure 7. The joint pdfs of ![]() with
with ![]() in the isosurface of
in the isosurface of ![]() had the largest probability density of the mode in the isosurfaces of
had the largest probability density of the mode in the isosurfaces of ![]() in each Lewis number case. In case Ml,
in each Lewis number case. In case Ml, ![]() was insensitive to
was insensitive to ![]() in the isosurface of
in the isosurface of![]() , and had no correlation with
, and had no correlation with ![]() in other isosurfaces of
in other isosurfaces of![]() . In case Mm, Mh,
. In case Mm, Mh, ![]() had positive correlations with
had positive correlations with ![]() in the isosurface of
in the isosurface of![]() , and had indefinite but slightly positive correlations with
, and had indefinite but slightly positive correlations with ![]() in other isosurfaces of
in other isosurfaces of![]() . The isosurface of
. The isosurface of ![]() is where the temperature gradient indicates a maximum value, and thus where the dilation effect of the flame is strongest.
is where the temperature gradient indicates a maximum value, and thus where the dilation effect of the flame is strongest. ![]() had a clear correlation with
had a clear correlation with ![]() in the isosurface of
in the isosurface of ![]() because the flame displacement speed is affected by the dilation effect of the flame [4] . The reason that
because the flame displacement speed is affected by the dilation effect of the flame [4] . The reason that ![]() was insensitive to
was insensitive to ![]() in the isosurface of
in the isosurface of ![]() in case Ml is considered to be the suppression of the dilation effect due to the predominance of the mass diffusion over the thermal diffusion in lower Lewis number than unity. The correlation coefficients of
in case Ml is considered to be the suppression of the dilation effect due to the predominance of the mass diffusion over the thermal diffusion in lower Lewis number than unity. The correlation coefficients of ![]() with
with ![]() on each isosurface of
on each isosurface of ![]() in the different Lewis number cases are shown in Figure 8. The correlation coefficient in the isosurface of
in the different Lewis number cases are shown in Figure 8. The correlation coefficient in the isosurface of ![]() was highest and more than twice value in the case of
was highest and more than twice value in the case of ![]() in each Lewis number case. This means that
in each Lewis number case. This means that ![]() involving the local flow velocity is more appropriate definition of the experimental flame displacement speed than
involving the local flow velocity is more appropriate definition of the experimental flame displacement speed than ![]() involving the mean inflow velocity.
involving the mean inflow velocity.
By comparing two kinds of experimental flame displacement speeds—involving the mean inflow velocity and the local flow velocity—with the numerical flame displacement speed, it was found that even if under the weak turbulence conditions in this study the local flow velocity is required to define the experimental flame displacement speed appropriately. However, the correlation coefficient which does not reach 0.6 is not so high, thus it is necessary to investigate the way to involve the local flow velocity in detail. Moreover, the fact—the correlation coefficient between the experimental and numerical flame displacement speeds is affected by Lewis number—means that the current experimental definition of the flame displacement speed is insufficient. It is also necessary to consider the way to incorporate the mass diffusion and the thermal diffusion into the definition of the experimental flame displacement speed.
4. Conclusion
The experimental measurement and analysis of the flame displacement speed were simulated using the DNS data of turbulent premixed flames with the different Lewis numbers, and the flame displacement speed obtained with simulating the experimental measurement and analysis was compared with the displacement speed numerically evaluated by the transport equation. The simulated experimental flame displacement speed involving the mean inflow velocity had no correlation with the numerical flame displacement speed, while the simulated displacement speed involving the local flow velocity had a clear correlation with the numerical displacement speed in the cases of higher Lewis number than unity. The correlation coefficient of the simulated displacement speed involving the local flow velocity with the numerical displacement speed had a maximum value on the isosurface of the reaction progress variable with the maximum temperature gradient where the dilation effect of the flame was strongest. Towards a more appropriate experimental flame displacement speed, it is necessary to
![]()
Figure 7. Joint pdfs between non-dimensionalised ![]() and
and ![]() on some isosurfaces of cT with different Lewis numbers. From the top, case Ml, case Mm, and case Mh, and from the left, cT = 0.167, 0.690, 0900.
on some isosurfaces of cT with different Lewis numbers. From the top, case Ml, case Mm, and case Mh, and from the left, cT = 0.167, 0.690, 0900.
![]()
Figure 8. Correlation coefficients between non-dimensionalised ![]() and
and ![]() on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
on some isosurfaces of cT with different Lewis numbers. From the left, case Ml, case Mm, and case Mh.
consider the treatment of the local flow velocity and the mass and thermal diffusions in the definition of the experimental displacement speed.
Nomenclature
![]() Reaction progress variable
Reaction progress variable
![]() Lewis number
Lewis number
![]() Integral length scale
Integral length scale
![]() Unit normal vector to a flame surface
Unit normal vector to a flame surface
![]() Reynolds number based on integral length scale
Reynolds number based on integral length scale
![]() Reynolds number based on Taylor microscale
Reynolds number based on Taylor microscale
![]() Temperature
Temperature
![]() Flow velocity vector
Flow velocity vector
![]() Turbulence intensity
Turbulence intensity
![]() Flame displacement speed evaluated by the transport equation
Flame displacement speed evaluated by the transport equation
![]() Flame displacement speed obtained in consideration of the mean inflow velocity on the upstream boundary
Flame displacement speed obtained in consideration of the mean inflow velocity on the upstream boundary
![]() Flame displacement speed obtained in consideration of the normal component of the local flow velocity
Flame displacement speed obtained in consideration of the normal component of the local flow velocity
![]() Mean inflow velocity
Mean inflow velocity
![]() Laminar burning velocity
Laminar burning velocity
![]() Turbulent burning velocity
Turbulent burning velocity
![]() Total volume of the computation domain
Total volume of the computation domain
![]() Mass fraction
Mass fraction
![]() Angle between u and n
Angle between u and n
![]() Measurement time interval
Measurement time interval
![]() Displacement vector of a flame
Displacement vector of a flame
![]() Flame thickness
Flame thickness
![]() Taylor microscale
Taylor microscale
![]() Density
Density
Superscripts
![]() Without flame stretch
Without flame stretch
![]() At the time t
At the time t
![]() At the time
At the time ![]()
Subscripts
![]() In adiabatic condition
In adiabatic condition
![]() In burned product
In burned product
![]() In unburned mixture
In unburned mixture