Safe Bounds in Semidefinite Programming by Using Interval Arithmetic ()
1. Introduction
We consider the standard primal semidefinite program in block diagonal form:
 (1)
(1)
where  is the cost vector,
is the cost vector,  is the variables vector and the matrices
is the variables vector and the matrices  are matrices in
are matrices in . Recall that
. Recall that  denotes vector space of real symmetric
denotes vector space of real symmetric  matrices and
matrices and  means that
means that , the cone of positive semidefinite matrices in
, the cone of positive semidefinite matrices in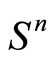 .
.  is the optimal value of the primal objective function. The standard inner product on
is the optimal value of the primal objective function. The standard inner product on 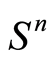 is:
is:

The dual semidefinite program of (1) is:
 (2)
(2)
with  and
and  is the optimal value of the dual objective function.
is the optimal value of the dual objective function.  is a feasible (minimum) and (or optimal) solution of the primal semidefinite problem (1) and
is a feasible (minimum) and (or optimal) solution of the primal semidefinite problem (1) and  is a feasible (maximum) and (or optimal) solution of the dual semidefinite problem (2). The duality theory for semidefinite programming is similar to its linear programming counterpart, but more subtle (see for example [1] -[3] ). The programs satisfy the weak duality condition:
is a feasible (maximum) and (or optimal) solution of the dual semidefinite problem (2). The duality theory for semidefinite programming is similar to its linear programming counterpart, but more subtle (see for example [1] -[3] ). The programs satisfy the weak duality condition: .
.
Interior point methods are a certain class of algorithms to solve most of semidefinite programs [4] -[7] . However, due to the use of floating point arithmetic, these algorithms may produce erroneous results. That is to say, when run on a computer, the result of these algorithms could be an overestimation or, worst, an underestimation of the very global optima. The purpose of this article is to show how rigorous error bounds for the optimal value can be computed by carefully post processing the output of a semidefinite programming solver. We use interval computation to rigorously bound the global optima. Thus the use of outward rounding allows a safe bounding of the global optima. There exist many solvers of semidefinite programs which provide tight bounds as pointed out in Roupin et al. (see, e.g., [8] ), however they are unsafe. That is why we propose here to embed safe semidefinite relaxations in an interval framework.
Before going into details, let us show, in a small example, a flaw or lack of rigor on the computation of the optimal value of the objective function [9] . Consider the following optimization problem:
 (3)
(3)
As shown in Figure 1, the solution of problem (3) lies in the neighbourhood of point . This point is the unique intersection of curve
. This point is the unique intersection of curve  and curve
and curve . However, at point
. However, at point , two curves are only separated by small distance of 10−5. Using Baron (6.0 and 7.2) [9] , a solver based on the techniques of relaxations, in particular linear and convex relaxations, quickly it finds 0 as global minimum even if the precision is enforced up to
, two curves are only separated by small distance of 10−5. Using Baron (6.0 and 7.2) [9] , a solver based on the techniques of relaxations, in particular linear and convex relaxations, quickly it finds 0 as global minimum even if the precision is enforced up to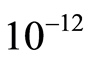 . Such a flaw is particularly annoying: as pointed out in [10] , there are many situations, like safety verification problem or chemistry, where the knowledge of the very global optima is critical.
. Such a flaw is particularly annoying: as pointed out in [10] , there are many situations, like safety verification problem or chemistry, where the knowledge of the very global optima is critical.
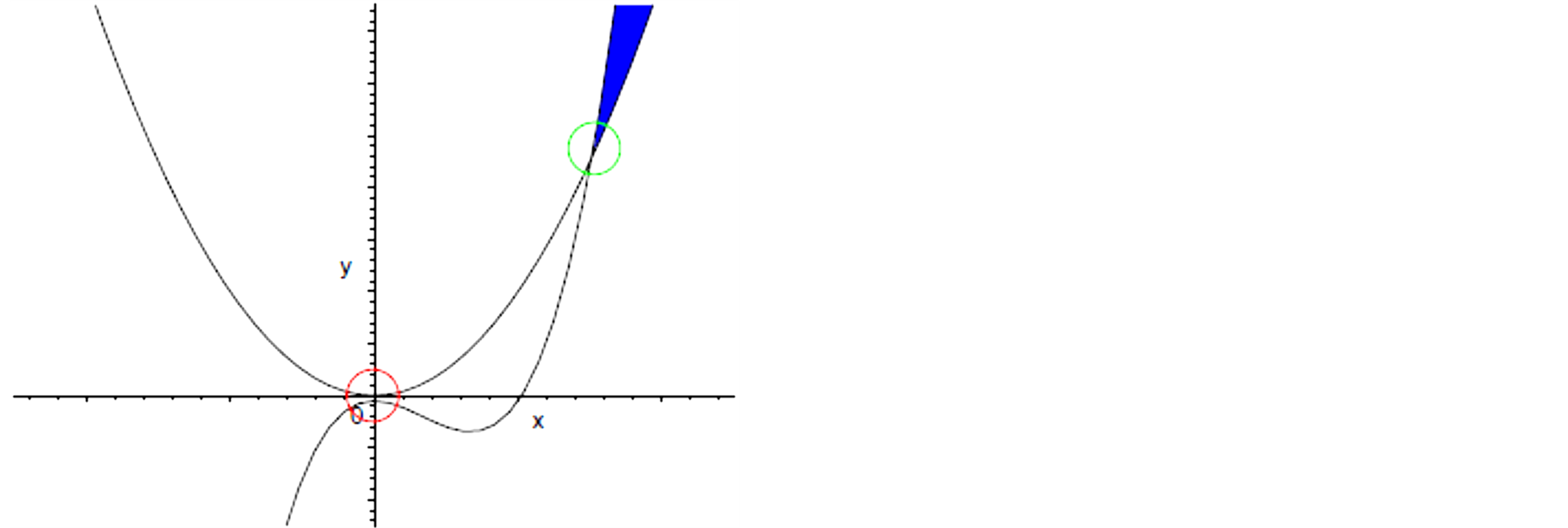
Figure 1. Geometrical representation of Problem (3).
The rest of this paper is organized as follows. The next section contains notations. In Section 3 an overview of the use of a procedure to compute a rigorous semidefinite bound is considered, and Section 4 contains numerical results. Finally, in Section 5, we provide some concluding remarks.
2. Notations, Interval Arithmetic
We require only some elementary facts about interval arithmetic, which are described here. There are a number of textbooks on interval arithmetic and selfvalidating methods that we highly recommend to readers. These include Alefeld and Herzberger [11] , Moore [12] , and Neumaier [13] .  is called an interval vector with lower bound
is called an interval vector with lower bound  and upper bound
and upper bound .
. ,
,  denote indifferently intervals and vectors of intervals, also called boxes. The width
denote indifferently intervals and vectors of intervals, also called boxes. The width  of the interval
of the interval  is the quantity
is the quantity . The interval evaluation of a real-valued function
. The interval evaluation of a real-valued function  is an interval
is an interval .
.  and
and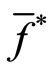 , respectively, denote lower and upper bounds of
, respectively, denote lower and upper bounds of , the optimal value of the objective function
, the optimal value of the objective function . For interval vector
. For interval vector  we define
we define  and
and  All interval operations can be easily executed by working appropriately with the lower and upper bounds of the intervals.
All interval operations can be easily executed by working appropriately with the lower and upper bounds of the intervals.
3. Rigorous Lower Bound
Semidefinite programs are typically used in branch-and-bound algorithms, to find lower bounds on the objective that allow one to decide whether a given node in the branch tree can be fathomed. For reliable results, it is therefore imperative that the computed lower bound is rigorously valid. However, the output of semidefinite programming routine is the result of an approximate calculation and hence is itself approximate. Obtaining rigorous error bounds for the solution of semidefinite problems is a difficult task [14] . Fortunately, it is possible to post process the approximate result to obtain rigorous bounds for the objective with reasonable effort, using directed rounding and interval arithmetic. The most famous implementation of this approach with linear relaxations are documented by many applications and a number of survey papers (for example Lebbah et al. [9] ). Recently, Neumaierand Shcherbina [15] proposed in the context of linear programming a safe procedure mathematically proven witch computes bound and guarantees its rigor. We introduce in this paper an extension of this procedure on semidefinite programming.
As pointed out in Neumaier and Shcherbina [15] , using directed rounding and interval arithmetic, cheap post processing of the linear programs arising in branch and bound framework can guarantee that no solution is lost. In mixed integer programming, linear programs are typically used to find lower bounds on the objective that allow one to decide whether a given node in the branch tree can be fathomed. For reliable results, it is therefore imperative that the computed lower bound is rigorously valid.
However, the output of a linear programming routine is the result of an approximate calculation and hence is itself approximate [16] . Obtaining rigorous error bounds for the solution of linear programming problems is a difficult task (cl. KRAWCZYK [17] , JANSSON [18] , JANSSON & RUMP [19] ).
Fortunately, it is possible to post process result to obtain rigorous bounds for the objective with reasonable effort, provided that reasonable bounds on all variables are available. Such bounds are frequently computed anyway in a preprocessing phase using a limited form of constraint propagation, and if the latter is done with sufficient care (using directed rounding to ensure the mathematical validity of each step of the process) [20] [21] , these bounds on the variables are rigorously valid.
We begin by looking at the simpler case where the linear program is given in the standard form.
 (4)
(4)
Its dual is
 (5)
(5)
Thus a rigorous lower bound 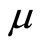 for
for  is obtained as follows.
is obtained as follows.

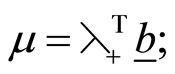
 (6)
(6)
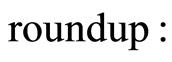
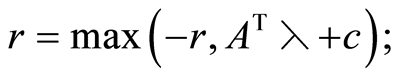


Of course, there are a variety of other ways of doing the estimates, e.g., using suitable case distinctions, and a high quality implementation would have to test which one is most efficient.
We use the extension of this result to semidefinite program. We solve the semidefinite program (8) below and its dual (9) with the SDPA [4] , a software package for solving semidefinite programs. It is based on a Mehrotratype predictor-corrector infeasible primal-dual interior-point method [5] [6] . We post process the output of the solver to obtaining rigorous error bounds for the optimal value.
To simplify the formulas, we use:
 (7)
(7)
So the primal semidefinite program (1) is written:
 (8)
(8)
And the dual semidefinite program (2) is written:
 (9)
(9)
The corollary below gives a rigorous value of the approximate optimal solution of the semidefinite program.
Corollary 3.1.
 (10)
(10)
With  where
where  and
and  are finite real numbers, and
are finite real numbers, and .
.
Proof: Solving the problem with the SDPA solver, we obtain  an approximate solution of the primal program (8) and
an approximate solution of the primal program (8) and 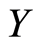 an approximate solution of the dual program (9). We obtain the corollary as follows:
an approximate solution of the dual program (9). We obtain the corollary as follows:

 is the residuel
is the residuel , so we obtain:
, so we obtain:
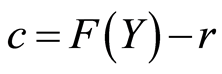


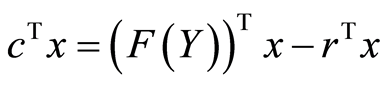
We replace F(Y) with its expression (7), we obtain:
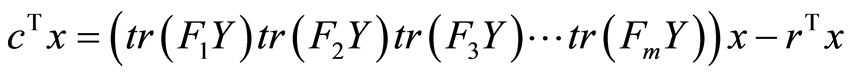
Knowing that  we obtain:
we obtain:
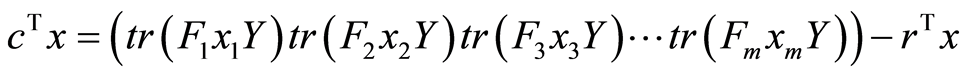
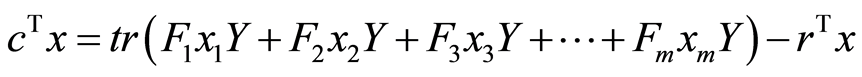

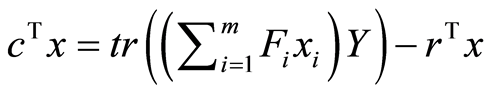
From the problem (1), we have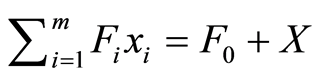 , so we obtain:
, so we obtain:
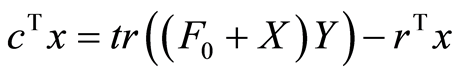
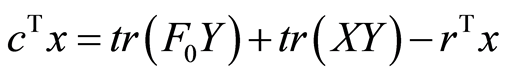
And thus:
 (11)
(11)
Extending (11) on the intervals, and assuming that rigorous two-sided bounds 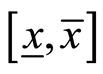 on x are available, and the two-sided bounds
on x are available, and the two-sided bounds  on r are obtained by simple interval computation. We obtain the final formula that provides a rigorous lower bound of
on r are obtained by simple interval computation. We obtain the final formula that provides a rigorous lower bound of 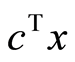
 (12)
(12)
Inexact arithmetic, r = 0, and we have at the optimum  (complementary slackness between
(complementary slackness between  and
and  from the optimality conditions). Then in (12) we obtain
from the optimality conditions). Then in (12) we obtain  which is consistent with the duality theorem (at the optimum, the primal objective
which is consistent with the duality theorem (at the optimum, the primal objective  is equal to the dual objective
is equal to the dual objective ).
).
This result is used to have a lower bound of the objective function and then we assumed the completeness of the algorithm branch and bound.
4. Global Optima
To solve optimization problem, the branch-and-bound procedures sequentially generate semidefinite programming relaxations. However, due to the rounding errors, relaxation thus may overestimate, or worst, underestimate the very global optima [22] . A consequence is that the global optima may be cut off. To avoid this disadvantage we can apply the algorithms for computing rigorous bounds described in the previous sections. Therefore, the computation of rigorous error bounds, which take account of all rounding errors and of small errors, is valuable in practice.
Therefore the experimentation results show that by properly post processing the output of a semidefinite solver, rigorous error bounds for the optimal value can be obtained.
The relaxation is solved with the SDPA which handles the standard form of the SDP problem and its dual. The quality of the error bounds depends on the quality of the computed approximations and the distances to dual and primal infeasibility. By comparing these bounds, one knows whether the computed results are good.
5. Experimentations Numerical Results
In this section, we present some numerical experiments for solving rigorously semidefinite problems. The results were obtained by using the solver SDPA witchhandles the standard form of semidefinite program and its dual [4] .
To test our procedure of correction, we generated linear programs automatically and particular quadratic programs, for which we know the primal objective value. We thus allow to validate our procedure in experiments with comparison. The solver SDPA solves the semidefinite relaxation of the problem considered and then we apply our procedure to the results.
The motivation to consider these examples is to show the effectiveness and the realizability of our procedure.
We consider the linear program:
 (13)
(13)
And we consider the quadratic program:
 (14)
(14)
We use the standard format of the Input Data File. In [23] the structure of the input SDP problem file is given as follows:
Title and comments m—number of the primal variables 
nBLOCK—number of blocks bLOCKsTRUCT—block structure vector
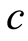
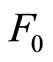
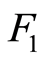
.
.
.
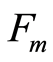
SDPA handles  matrices blocks. This strategy minimizes the computational cost during SDP problem solving. It uses the term number of blocks noted Nblock.
matrices blocks. This strategy minimizes the computational cost during SDP problem solving. It uses the term number of blocks noted Nblock.
The SDPA stores computational results in the output file such as an approximate optimal solution, the total number of iteration, the primal objective function value, the dual objective function value and other final informations.
Table 1 and Table 2 present the results of our experimentations. In these tables, Prob is the problem (13) in Table 1 and the problem (11) in Table 2, m is the number of variables, P is the approximate objective function  of the problem (10) gives by SDPA solver, PC is the rigorous objective function
of the problem (10) gives by SDPA solver, PC is the rigorous objective function  gives by our procedure , safe is a flag that indicates whether the objective function is rigorous (+) or not (−), Ex is the exact value of objective function and Ec is the gap (Ex – PC).
gives by our procedure , safe is a flag that indicates whether the objective function is rigorous (+) or not (−), Ex is the exact value of objective function and Ec is the gap (Ex – PC).
Below, some results are presented, obtained on some well-known benches with the branch and bound solver. Audet’s problems come from his thesis [24] . The presented results can be viewed as a further development of similar methods for linear programming.
Table 3 presents the results of our experimentations of global bound. In this table, Prob is the problem to solve, m is the number of variables, n is the number of constraints, Ntot is the total of nodes, Nopt is the optimal node, Lower is the rigorous objective function of the problem gives by our procedure with SDPA solver, Upper is the upper bound, and CPU is the time in second required to solve the problem.
We note that throughout the test database, our solver supervises the actual optimal solution always correctly. This rigor in resolution with the SDPA solver is crucial because it guarantees us completeness.
Therefore, their integration into the branch and bound algorithms is plausible.
These results show that the use of interval arithmetic computation gives rigorous bounds. We can always use filtering techniques and parallelism to optimize the quality of the solution and the CPU time.

Table 1. Rigorous lower bound of problem (13).

Table 2. Rigorous lower bound of problem (14).

Table 3. Global optima Audet’s problems.
6. Conclusion and Future Works
The computation of rigorous error bounds for semidefinite optimization problems can be viewed as a carefully post processing tool that uses only approximate solutions computed by a semidefinite solver. In this paper, we have introduced a safe and efficient framework to compute a rigorous solution of semidefinite relaxation of a nonlinear problem. Our numerical experiments demonstrate that, roughly speaking, rigorous lower bounds for the optimal value are computed even for semidefinite programs. The numerical results show that such rigorous error bounds can be computed even for problems of large size.