Explaining Perceived Inconsistencies in “Stated Preference” Valuations of Human Life ()
1. Introduction
Frequently used by governments to set policy, economic measurements can have a great influence on the way in which we live our lives. If there is a free market in the good, then the measurement task reduces simply to finding the price on which buyer and seller agree. However, there are and always will be instances where no obvious market exists and yet it is still desirable to know what value people place on the amenity so that a cost-benefit analysis may be carried out. This applies in the case of public goods such as clean air or the continued survival of a rare species of plant or animal. In particular, it applies also to the very important valuation of human life, which is essential if rational choices on safety systems are to be made.
“Revealed preferences” may enable an inferential measurement of the value of the non-market good to be made. Such methods conform to John Locke’s precept: “I have always thought the actions of men the best interpreters of their thoughts”, with the good’s value determined through observing what quantifiable benefit has been given up in order to secure a certain quantity of that good or a proxy, or else, if the good is undesirable, what quantifiable burden has been taken on to avoid it. Clearly, the revealed preference technique requires a model of the system, and, as a minimum, that model needs to be transparent so that it can be examined in full detail by a person possessed of the necessary mathematical skills. The J-value method [1] -[3] , based on the Life Quality Index [4] -[7] , is an example of a revealed preference technique applied to safety analysis and the valuation of human life that conforms to these transparency requirements.
However, attempts may be made to measure the value of a non-market good using opinion polling or market survey techniques. These “stated preference” methods are sometimes referred to as “contingent valuation” (CV) [8] . In the stated preference approach, members of a representative sample of the population considered to have consultation rights are asked more or less directly to state their maximum acceptable price (MAP) for the non-market good. As with other opinion polls and market surveys, it is then assumed that an opinion that is in some sense representative of an entire population can be deduced fairly accurately from the collections of such statements made by people in a random sample.
This paper will provide a new analysis of the stated preference approach used by a research team commissioned by the UK Health and Safety Executive (HSE), the UK Department of the Environment, Transport and the Regions, the UK Home Office and the UK Treasury to investigate how much people were willing to pay for measures to protect human life [9] . The study was tasked with estimating for the UK Government the “value of a prevented fatality” (VPF), the maximum amount that it is notionally reasonable to pay for a safety measure that will reduce by one the expected number of preventable premature deaths in a large population.
The VPF is assumed to be the same for all people in the UK, irrespective of age or gender, an assumption that has been questioned elsewhere (e.g. [1] -[7] [10] -[12] ). But whatever problems exist with its scientific and philosophic status, the VPF figure, published annually by the UK Department for Transport, is important [13] . Updated to account for changes in gross domestic product (GDP) per head, it is used extensively in the UK as a reference not only by Government departments but also by the Health and Safety Executive. Moreover, its adoption by the HSE has led to its widespread use in UK industry, road and rail transport, chemical and nuclear, as a standard for judging how much should be spent on protection measures aimed at reducing risks to life.
However the project team commissioned to carry out the research reported problems with their findings, concluding [9] that:
“One can therefore have little confidence that the VOSL (‘value of a statistical life’, used synonymously with VPF) estimates that emerged from these studies can be used as a reliable basis for public policymaking.”
and labelled their study “Caveat Investigator”—“let the investigator beware”. The Caveat Investigator team came to believe that people could not be expected to answer accurately on how much they would spend to reduce further an already low risk of a fatal injury. So, in a follow-on study for the same sponsors, the Caveat Investigator team decided to seek an estimate of the VPF indirectly, by asking people to consider a lesser injury first, with which they considered people would be better able to cope. They then interpreted the new survey data using the “two-injury chained method”, which depends on a fairly involved application of utility theory [14] . According to Wolff and Orr [15] , the resulting figure has become the standard used in the UK:
“It appears that the Carthy study is now the primary source of VPF figures, adjusted for inflation and changes in GDP.”
Moreover, despite the fact that it has been many years since the survey was made, a 2011 report for the Department for Transport, with authors in common with the Carthy study, recommended “against any early new full scale WTP (willingness to pay) study” [16] .
However, considerable problems exist with the validity of the VPF coming from the Carthy study. The validation of the chained method is regarded by Wolff and Orr [15] as “severely challenging”:
“The method needs to make assumptions about the shape of an average person’s utility function, connecting their attitudes to small risks with their attitudes to the much larger risks that are presented to the subject. Yet the testing of any such assumption, and hence the validation of the method, presents severe challenges. In order to test the chained method it appears necessary to elicit individual willingness to pay for very small changes in risk so they can be compared with attitudes to larger changes. However, if it were possible to elicit such preferences then the chained method would not be necessary; it was introduced precisely because it has so far proven impossible to elicit such preferences in any reliable way. In short, if it were possible to validate the chained method, it would not be necessary.”
In fact a fair test of the validity of the chained method using no more data than was available at the time to Carthy et al. has now been carried out [17] . The two-injury chained method is found there to fail multiple tests of its validity, so that, unfortunately, no reliance can be placed on the team’s second attempt at producing a VPF figure. This returns the focus to the team’s initial attempt, reported in [9] . Were the authors right to dismiss that survey or were the results a valid set of stated preferences?
The Relative Utility Pricing model [18] [19] will be used in this paper to shed light on the question.
2. The Problems Reported in the Caveat Investigator Study
In what the authors subsequently named the “First Phase” of the Caveat Investigator study (hereafter referred to as “Phase 1” for compactness), a number respondents were asked to say how much they would be prepared to pay for a number of safety improvements that would reduce their annual risks of death and injury in road accidents. The Caveat Investigator team attempted to test the sensitivity of their results to the magnitude of the risk reduction by including two reductions in the frequency of a fatal accident, labelled [F1] and [F3]. [F1] gave a 1 in 100,000 reduction in the annual frequency per person of death in a road accident while [F3] gave a 3 in 100,000 reduction in the annual frequency per person of death on the road.
In Phase 1, 83 respondents were divided into two groups: 41 people were assigned to the Bottom Up (BU) group and 42 to the Top Down (TD) group. The TD number was later reduced effectively to 40 through the censoring of the opinions of two people, for the reasons given in the note to Table 1 of [9] :
“One outlier has been removed from the TD sample (a respondent in the lowest income group category whose first willingness to pay response was £5,000). In addition, one respondent in the TD group failed to give revised CV responses.”
Each person, i, in the BU group is asked to provide his maximum acceptable price (MAP),  , for [F1] first and his MAP,
, for [F1] first and his MAP,  , for [F3] next, and so in the knowledge that the smaller reduction [F1] is an option. Taking the initial letter from “valuation”, the term,
, for [F3] next, and so in the knowledge that the smaller reduction [F1] is an option. Taking the initial letter from “valuation”, the term, 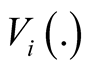 , uses upper case lettering to denote a random variable, in line with the proposition that the respondents and hence their opinions are selected at random.
, uses upper case lettering to denote a random variable, in line with the proposition that the respondents and hence their opinions are selected at random.
Conversely each person in the TD group is invited to name his MAP,  , for [F3] first and his MAP,
, for [F3] first and his MAP,  , for [F1] second. Thus he is unaware of the smaller, [F1] option when making his initial valuation of [F3]. However it is stated that respondents
, for [F1] second. Thus he is unaware of the smaller, [F1] option when making his initial valuation of [F3]. However it is stated that respondents
“had also been given every opportunity to revise their responses after having been presented with a summary of their answers to the full sequence of CV questions”
with a respondent failing to give to give revised CV responses being excluded from the survey, as shown in an earlier quotation in this Section. Hence the person will be aware of the smaller option, [F1], when he makes his final valuation of [F3].
But the analysts attempting to find the VPF (or VOSL) from the results detected a non-obvious pattern in the responses associated with safety measures, [F1] and [F3], and became concerned at the ratio of the stated values assigned by the respondents to [F1] and [F3]. While they were prepared to concede on economic grounds that the value,  , placed by respondent, i, on [F3] would not be as high as three times the value,
, placed by respondent, i, on [F3] would not be as high as three times the value,  , he placed on [F1], the analysts were not prepared to accept the very much lower values for
, he placed on [F1], the analysts were not prepared to accept the very much lower values for  that they found.
that they found.
The phenomenon of  is observed in both the TD group and the BU group. (The symbol
is observed in both the TD group and the BU group. (The symbol  is used here as meaning “significantly less” as defined in Table 5 and Table 6, which show that there are a good many instances where
is used here as meaning “significantly less” as defined in Table 5 and Table 6, which show that there are a good many instances where .) In fact, something similar had been observed in previous studies:
.) In fact, something similar had been observed in previous studies:
“This inverse relationship between the VOSL and the magnitude of risk reduction is evident in the results of earlier CV studies.12
12. For within-study evidence of the effect, see for example Jones-Lee et al. (1985) or Jones-Lee et al. (1995). To the best of our knowledge the only attempt to explore the relationship between estimates of the VOSL and the magnitude of the risk reduction in CV questions on a between-study basis is that reported in Beattie et al (1998) where the inverse relationship between the VOSL (taken as the sample mean MRS of wealth for risk for each study) and the magnitude of the risk reduction,  , is found to be highly significant with
, is found to be highly significant with  .”
.”
Nevertheless not only the project team but also their sponsors became concerned at the phenomenon observed and
“It was felt by both the research team and the project sponsors that the type of question used in the First Phase study could not be employed with any confidence as a basis for obtaining direct empirical estimates of WTP-based values of safety for use in public policymaking.”
As a result a “Second Phase” of the Caveat Investigator study was initiated, hereafter known as “Phase 2”. Whereas Phase 1 was concerned with non-fatal injuries as well as deaths, Phase 2 was to be a smaller study, dealing only with fatalities.
In Phase 2 all respondents are asked first to imagine that there is a program of road safety improvements affecting the area where they live, assumed to contain a population of 1 million people living in 400,000 households. 52 respondents, divided into two equal groups, given the identifiers, Version A (VA) and Version F (VF), are asked first to place a value to their household on an improvement [R3] that will prevent a number of deaths on the roads over a specified period in the area in which they live. Then they are asked to value another safety improvement [R1] that will prevent a third of that number.
For VA respondents, [R3] is a reduction of 15 road deaths over 1 year, while [R1] is a reduction of 5 road deaths over 1 year. Meanwhile, for VF respondents, [R3] is a reduction of 75 road deaths over 5 years, while [R1] is a reduction of 25 road deaths over 5 years. The valuations sought are first for [R3] and then for [R1], in both VA and VF, but once again the respondents are given the opportunity to revise their initial responses. Moreover, they are also asked the question:
“In the past, we’ve found that some people say that preventing 15/75 deaths on the roads are worth three times as much to them as preventing 5/25 deaths on the roads: but other people don’t give this answer. Can you say a bit about why you gave the answers you did?”
This question was intended to carry out the analysts’ wish
“to focus respondents’ attention on the relative magnitudes of the two reductions in road fatalities.”
and might, indeed, be regarded as giving a rather clear steer on the analysts’ concerns.
But once again it is found that respondents in both VA and VF groups tend to give valuations  in the same way as
in the same way as  characterised the responses of the two groups, BU and TD, in Phase 1 of the research.
characterised the responses of the two groups, BU and TD, in Phase 1 of the research.
Following the calculation of the corresponding VPFs in the manner described in Section 11 of this paper, a further concern is raised, namely that each of the VPFs generated (£9.83 M and £4.63 M from Phase 1, £8.70 M and £3.87 M from Phase 2) is much higher than the VPF value then in use (£902,500 in 1997 prices [14] ):
“Furthermore, when the VOSL estimates that they had collectively generated were fed back to respondents in the course of the third-stage follow-up discussions, it was widely felt that the figures concerned were excessive.21
21. In order to put the VOSL figures into perspective, respondents were given some idea of, for example, the approximate number of secondary school teacher-years or hip replacement operations that could be financed by the sums concerned.”
The extent and scope implied by the phrase, “it was widely felt”, is not clarified either in the main text or the footnote.
Ultimately the Caveat Investigator team became so concerned over the “aberrant response patterns” that they found, specifically that ,
, 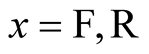 for many individuals, that they rejected all the results of their study and decided to start again. But are the response patterns, some signs of which are acknowledged to have been seen before, “aberrant”, or are they the sort of thing one should expect when asking people to state their valuations of two “safety packs”, with pack 2 being three times the size of pack 1?
for many individuals, that they rejected all the results of their study and decided to start again. But are the response patterns, some signs of which are acknowledged to have been seen before, “aberrant”, or are they the sort of thing one should expect when asking people to state their valuations of two “safety packs”, with pack 2 being three times the size of pack 1?
3. Results of the Caveat Investigator Study
The safety measures offered and results of the Caveat Investigator study are summarized in Tables 1-6.

Table 1. Reductions in annual fatality frequency for Phase 1.

Table 2. Reductions in deaths and annual frequency of fatality for Phase 2.

Table 3. Phase 1 mean MAPs, standard deviations (s.d.), standard errors (s.e.) and medians.

Table 4. Phase 2 mean MAPs, standard deviations (s.d.), standard errors (s.e.) and medians.

Table 5. Individual MAP ratios for Phase 1, .
.
a9 ratios, RFi, were listed as “Missing” under TD as well as 5 under BU in Table 2 of Beattie et al. Meanwhile Note 11 of Beattie et al. reads: “In addition, 8 respondents gave a zero willingness to pay for both [F1] and [F3] while a further 6 gave a zero response for [F1] but a non-zero response for [F3]. Clearly CV[F3]/CV[F1] ratios cannot be computed for any of these 14 cases.” In the absence of more precise information, these 6 respondents have been distributed equally in Table 5 between TD and BU.

Table 6. Individual MAP ratios for phase 2, .
.
Table 1 and Table 2 give descriptions of the reductions in fatal accident frequency and fatal accidents over a period for Phase 1 and Phase 2 that the respondents are asked to value.
Table 3 and Table 4 give the mean valuations of such reductions. Note: the practice used by the Caveat Investigator team has been retained, whereby the monetary values placed on the 5-year safety programmes of VF have been divided by 5 to give annualized amounts.
Table 5 and Table 6 classify the ratios 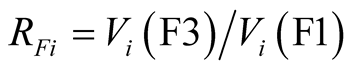 and
and . The ratios are categorized as one of: incomputable, equal to 1, between 1 and 2, between 2 and 3 or above 3.
. The ratios are categorized as one of: incomputable, equal to 1, between 1 and 2, between 2 and 3 or above 3.
This paper will now explain these findings and show that what the Caveat Investigator team describes as “aberrant response patterns” are, in fact, fully understandable outputs from an opinion survey aimed at finding the value to the public of safety improvements.
4. Safety Improvements as Commodities
The good offered in Phase 1 of the Caveat Investigator study is described as follows:
“a safety feature fitted to their car which would reduce their own risk of death or injury but would leave the risk to other occupants of the car unchanged. Respondents were also told that if it was to remain effective, the safety feature would have to be renewed every twelve months.”
with its merit described simply by a number “1 in 100,000 reduction of annual risk of death” for [F1] and “3 in 100,000 reduction of annual risk of death” for [F3].
The description is bare and factual with no attempt at product differentiation. No allusions are made to brand or to any potential status uplift from having the safety device fitted to the respondent’s car. It should be borne in mind that such promotional tactics might well be used by a commercial firm trying to sell its safety wares to a consumer. Thus a commercial vendor might, as a minimum, offer to attach a windscreen sticker to the car to show the enhanced safety performance that the driver has managed to procure.
It may be deduced from the fact that the investigators did not mention any additional benefits or kudos associated with the device that they intended not to cloud the issue in any way, but wanted to convey the safety content of the device as its only benefit. This absence of any attempt at product differentiation makes it reasonable to suppose that the respondents to whom the good was offered would have regarded it as a commodity. The good offered in the Phase 2 of the Caveat Investigator study is:
“a program of road safety improvements affecting the area in which they live, with a population of 1 million people, or approximately 400,000 households.”
again with its merit described simply by a number, under VA, the number of deaths averted in one year is 5 deaths for [R1] and 15 deaths for [R3], while under VF, the number of deaths averted in five years is 25 deaths for [R1] and 75 deaths for [R3]. The safety improvement offered is thus a public good with no attempt at product differentiation (difficult in any case for a public good). Hence, for Phase 2 of the Caveat Investigator study too, the good offered to the respondents may be regarded as a commodity.
5. Relative Utility Pricing (RUP) Model for Quantity Discounts
The RUP model, [18] -[20] , applies to commodities offered in packs of different sizes and is able to provide an economic explanation for sales promotions such as “buy-one-get-one-free” (BOGOF) and “3 for the price of 2”. While the RUP model is not meant to apply to differentiated goods, it has been shown in the previous section that the hypothetical safety goods being offered to the respondents in the Caveat Investigator surveys are not differentiated goods but commodities offered in different sizes. Using the terminology of pack sizes, the safety improvement of either [F]">]">1] and [R]">]">1] may be called “safety pack 1” , while safety improvements [F]">]">3] and [R]">]">3] may be termed “safety pack 2”. Because the safety packs are offered as commodities, the RUP model should apply to the Caveat Investigator study.
The relevant Equations for the RUP model are now presented for a commodity, B, that is sold simultaneously in packs of different sizes. Let 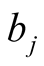 be the amount of commodity, B, contained in pack
be the amount of commodity, B, contained in pack :
: , where
, where  so that pack N is the largest pack on offer and pack 1 is the entry-level pack, while pack 0 represents the empty pack, equivalent to no purchase:
so that pack N is the largest pack on offer and pack 1 is the entry-level pack, while pack 0 represents the empty pack, equivalent to no purchase: . The “largeness”,
. The “largeness”,  , of pack
, of pack  is defined as its size relative to the entry-level pack 1:
is defined as its size relative to the entry-level pack 1:
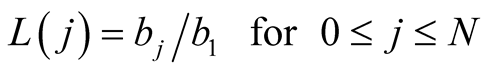 (1)
(1)
Thus the largeness of pack  is the number of standard units that pack
is the number of standard units that pack  contains, where a standard unit comprises the contents of pack 1, namely
contains, where a standard unit comprises the contents of pack 1, namely . Hence
. Hence  and
and .
.
In line with Kahneman and Tversky [2]">]">1] , who have argued that “people normally perceive outcomes as gains and losses [relative to the current asset position], rather than as final states of wealth or welfare”, a proposition supported by Thaler [22] , the approach is taken in [18] of considering the utility of the contents of the pack. The utility of the empty pack, with contents  will be
will be , the utility of the contents,
, the utility of the contents,  , of pack 1 will be
, of pack 1 will be , and, in general, the purchase of pack
, and, in general, the purchase of pack  will result in a utility,
will result in a utility, . Hence the gain in utility resulting from the purchase of pack 1 rather than pack 0 (equivalent to making no purchase) is
. Hence the gain in utility resulting from the purchase of pack 1 rather than pack 0 (equivalent to making no purchase) is
 (2)
(2)
Meanwhile the marginal utility gained,  , from the purchase of a pack
, from the purchase of a pack  rather than a smaller pack
rather than a smaller pack  is
is
 (3)
(3)
Thus
 (4)
(4)
As explained in [18] , the form of these utility differences,  ,
, 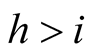 , is constrained by the requirement that
, is constrained by the requirement that

 (5)
(5)
where Equation (5) expresses the condition of “singular homogeneity”, as defined and discussed in Appendix A of that paper. Rearrangement of Equation (4) gives:
 (6)
(6)
and so, after rearrangement and the use of Equation (5):
 (7)
(7)
Considering the case of two packs, the standard economic assumption of a constant price per unit of marginal utility gained implies that  where
where  is the price associated with the marginal utility,
is the price associated with the marginal utility,  , gained by the purchase of pack 1, given that the purchase of pack 0 is possible, while
, gained by the purchase of pack 1, given that the purchase of pack 0 is possible, while  is the price associated with the marginal utility,
is the price associated with the marginal utility,  , gained by the purchase of pack 2, given that the purchase of pack 1 is possible. Hence
, gained by the purchase of pack 2, given that the purchase of pack 1 is possible. Hence  is the price achieved for pack 2 when the option exists to purchase pack 1 for price,
is the price achieved for pack 2 when the option exists to purchase pack 1 for price, .
.
Therefore
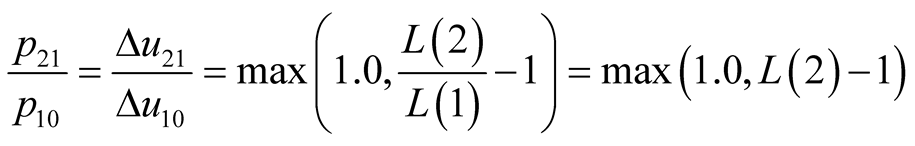 (8)
(8)
where the maximum function embodies the general economic assumption that, all other things being equal, less will not be preferred to more, while the largeness of the entry pack 1 is unity by Equation (1).
Equation (8) expresses a basic consumer preference that underlies the pattern of prices observed for different sizes of packs of diverse goods offered for sale in supermarkets and on the internet [18] [19] . It provides the rationale for the finding that “more than 80% of all promotional activity within supermarkets is a bogof [buy-oneget-one-free] or three-for-two” [2]">]">3] , as can be seen by setting the largeness ratio in Equation (8) to first 2 and then 3.
The ratio of pack sizes,  , is clearly equal to 3 in the case of the safety packs offered in the Caveat Investigator study:
, is clearly equal to 3 in the case of the safety packs offered in the Caveat Investigator study:
 (9)
(9)
Now  when pack 2 is three times as big as pack 1, and substituting this into Equation (8) gives the ratio of the prices the consumer will find acceptable:
when pack 2 is three times as big as pack 1, and substituting this into Equation (8) gives the ratio of the prices the consumer will find acceptable:
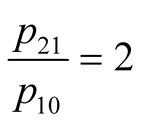 (10)
(10)
In the commercial world, of course, a bargain needs to be struck between vendor and buyer. Thus the valuation of the purchaser may be disputed and resisted by the vendor, who will be prepared to offer quantity discounts only if his variable costs are low enough for each sale to make a non-negative contribution to covering his overall costs. Economic theory suggests that the 3-for-the-price-of-2 sales promotions on the high street need to be consistent with the retailer maximizing his profit, which implies an optimization exercise to find the offered price, as proposed in [18] [19] . But the optimal price is the same as the mean of the MAPs in the target market when the probability distribution for MAP is uniform. Moreover the optimal price and the mean of the MAPs will always be very similar, no matter what probability distribution for MAP is assumed [24] [25] . Hence when a 3-for-the-price-of-2 sales promotion is offered, the mean ratio of the individual’s MAPs for packs 1 and 2 will be roughly two.
This suggests that the results described as “aberrant” by the Caveat Investigator team are an instance of 3-for-the-price-of-2 pricing observed frequently on the high street, which, as illustrated in Section 5 and in [18] and [19] , is driven by consumer preferences. Given the relative size of safety packs 1 and 2, RUP theory suggests that MAP ratios,  ,
,  , can be expected to be significantly less than 3. However the situation is complicated by the fact that the respondents’ powers of discrimination are being taxed by the small size of the safety packs on offer.
, can be expected to be significantly less than 3. However the situation is complicated by the fact that the respondents’ powers of discrimination are being taxed by the small size of the safety packs on offer.
6. The Limits of Discrimination
Beattie et al. recognized that people face problems of discrimination when the risk is already so small that they can distinguish no benefit or utility from reducing it further [9] . Thus the Caveat Investigator team decided before the start of Phase 1 that they would direct their attention to:
“those contexts (such as the roads) in which it was felt that base risks were ‘large’ enough to render CV questions concerning reductions in risk comprehensible to respondents. By contrast, in other contexts (such as rail or nuclear power generation) it would appear that base risks are so low that CV questions concerning reductions in those risks would involve probabilities that most members of the public would find great difficulty in conceptualising.”
Moreover, they concluded after Phase 1 that
“it appeared that a major contributory factor in the relative failure of the direct CV questions was the difficulty experienced by many respondents in dealing with small reductions in already small probabilities. For example, some respondents seemed to regard one probability reduction of 3 in 100,000 and another of 1 in 100,000 as being essentially the same, since both constitute such small absolute numbers.”
However, by selecting a population of 1 million people in Phase 2 and then casting [R3] and [R1] as reductions in road deaths of 15 and 5 per year respectively, the Caveat Investigator team are compelling the new groups of respondents to deal with even smaller reductions in annual frequency per person of fatality: 1.5 in 100,000 and 0.5 in 100,000. See Table 1 and Table2 Hardly surprisingly, a good many of the respondents in Phase 2 are pushed beyond their limit of discrimination:
“Far from attenuating the pronounced embedding effects encountered in the First Phase study, the Second Phase CV question format, if anything, appears to have exacerbated these effects, with 42% of respondents giving identical non-zero CV responses for [R3] and [R1], compared with the 28% of First Phase respondents who gave identical non-zero CV responses for [F3] and [F1].”
In fact the Caveat Investigator team appears to be half expecting this outcome:
“Previous evidence indicates that presenting risk information in this way in itself does not eliminate insensitivity to quantity” (italics are those of [9] )
but still maintains the hope that
“when used within the three-stage, in-depth study design outlined above, this alternative approach would increase the sensitivity of responses.”
In the event, it is clear that the team’s hope is not realized. One might speculate that the in-depth nature of the respondents’ participation could even have been a causal factor, since the respondents would have had the opportunity to set the raw numbers of deaths prevented in the context of a population of 1,000,000 people. For even a moment’s thought on the part of the respondent will transform the 5 deaths averted into a frequency of 5 in a million per person. Similarly, 15 deaths averted is easily translated into 15 in a million per person.
If pushed beyond his limit of discrimination, respondent i may suffer from one of 3 types of indiscrimination, in ascending order of severity:
Type 1, where the same non-zero value is placed on the utility of safety packs 1 and 2, as indicated by ;
; .
.
Type 2, where the utility of safety pack 1 is put at zero by setting 
 but the utility of safety pack 2 is considered greater than zero, so that
but the utility of safety pack 2 is considered greater than zero, so that ;
; ..
..
Type 3, where the value placed on the utility of both pack 1 and pack 2 is zero: ;
; .
.
A fourth type, Type 4, is theoretically possible, where the utility of safety pack 1 is valued positively so that ,
,  but safety pack 2 is valued at zero by putting
but safety pack 2 is valued at zero by putting ,
,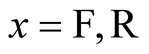 , but this goes against the normal economic principle that more is preferred to less, and does not feature in the results reported for the Caveat Investigator study. Indiscrimination Types 1, 2 and 3 are, however, all present in Phase 1 of the Caveat Investigator study, while Type 1 is present in Phase 2.
, but this goes against the normal economic principle that more is preferred to less, and does not feature in the results reported for the Caveat Investigator study. Indiscrimination Types 1, 2 and 3 are, however, all present in Phase 1 of the Caveat Investigator study, while Type 1 is present in Phase 2.
From Table 5, 23 people in the TD and BU groups combined suffer from Type 1 indiscrimination, for each of whom the ratio 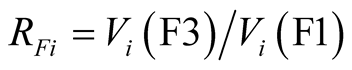 is unity. Moreover, 6 respondents suffer from Type 2 indiscrimination and 8 respondents are exhibiting type 3. This makes a total of 37 out of 81 respondents for which data are available who are suffering from a lack of discrimination of some type.
is unity. Moreover, 6 respondents suffer from Type 2 indiscrimination and 8 respondents are exhibiting type 3. This makes a total of 37 out of 81 respondents for which data are available who are suffering from a lack of discrimination of some type.
There is, unfortunately not enough information in the Caveat Investigator paper to distribute Types 2 and 3 indiscrimination over the two groups TD and BU with certainty. In its Table 2, the Caveat Investigator team lists 9 ratios,  , under TD as “missing” and 5 under BU. Meanwhile Note 11 of the study reads:
, under TD as “missing” and 5 under BU. Meanwhile Note 11 of the study reads:
“In addition, 8 respondents gave a zero willingness to pay for both [F1] and [F3] while a further 6 gave a zero response for [F1] but a non-zero response for [F3]. Clearly CV[F3]/CV[F1] ratios cannot be computed for any of these 14 cases.”
The 14 incomputable cases translate into the 14 “missing” cases, but no split between TD and BU is given. In the absence of more precise information, and to give indicative figures, it is assumed in Table 5 that the 6 respondents with Type 2 indiscrimination are distributed equally between TD and BU. This assumption is for illustrative purposes only and has no effect on the calculations or conclusions that follow.
Meanwhile for Phase 2, 22 out of 52 respondents exhibit Type 1 indiscrimination, for whom . 13 of these are in VA while 9 are in VF. See Table6
. 13 of these are in VA while 9 are in VF. See Table6
The RUP model presumes that the person assigning a price is able to distinguish the utility of pack 1 from the utility of the empty pack, viz. . Moreover the RUP model assumes that the person can discriminate between the utilities of pack 2 and pack 1, so that for a present pack-size ratio of 3, as in the present instance, C, which will be reflected in different prices for the two safety packs. Thus the RUP model should be applied only to those who do not suffer from indiscrimination of any type, and hence to the discriminating 44 out of the 81 respondents in Phase 1 and to the discriminating 30 out of the 52 respondents in Phase 2.
. Moreover the RUP model assumes that the person can discriminate between the utilities of pack 2 and pack 1, so that for a present pack-size ratio of 3, as in the present instance, C, which will be reflected in different prices for the two safety packs. Thus the RUP model should be applied only to those who do not suffer from indiscrimination of any type, and hence to the discriminating 44 out of the 81 respondents in Phase 1 and to the discriminating 30 out of the 52 respondents in Phase 2.
7. Piecewise Uniform Distribution for Discriminating Respondents; Extended Piecewise Uniform Distribution for All Computable MAP Ratios
It is reasonable to suppose that different discriminating respondents will give somewhat different MAP ratios,  ,
,  , and the question arises as to how to consolidate these different values into a single, representative figure. If the democratic principle is to be applied so that each person’s view is to be accorded the same respect, then the sample mean should be used, as it is the only known measure that satisfies the requirements of Structural View Independence (Thomas, 2014) and can thus absolve the analyst of the charge of bias.
, and the question arises as to how to consolidate these different values into a single, representative figure. If the democratic principle is to be applied so that each person’s view is to be accorded the same respect, then the sample mean should be used, as it is the only known measure that satisfies the requirements of Structural View Independence (Thomas, 2014) and can thus absolve the analyst of the charge of bias.
In fact [9] does not list the actual values of the individual MAP ratios, so that reliance must be placed upon the classified data as presented in Table 5 and Table6 Nevertheless it is possible, making only mild assumptions, to estimate the expected value of the MAP ratio for the discriminating respondents, as well as its variance.
Under the presumption that the Caveat Investigator team would have flagged any  or
or  ratios greater than 4.0 as noteworthy but does not mention any instances, it is assumed first that no respondent has an
ratios greater than 4.0 as noteworthy but does not mention any instances, it is assumed first that no respondent has an  or
or  ratio greater than 4.0. Hence the classifications,
ratio greater than 4.0. Hence the classifications,  in Table 5 and
in Table 5 and  in Table 6 may be replaced by
in Table 6 may be replaced by  and
and  respectively. It is now possible to fit a Piecewise Uniform distribution for
respectively. It is now possible to fit a Piecewise Uniform distribution for ,
,  , within each of the intervals, 1 - 2, 2 - 3 and 3 - 4.
, within each of the intervals, 1 - 2, 2 - 3 and 3 - 4.
Let the number of MAP ratios recorded in a given interval be , where
, where  denotes the interval between 1 and 2,
denotes the interval between 1 and 2,  denotes the interval between 2 and 3 and
denotes the interval between 2 and 3 and  denotes the interval between 3 and 4. The response of a discriminating respondent will be captured in one of the three intervals, and, assigning n to the total number of discriminating respondents, it is clear that
denotes the interval between 3 and 4. The response of a discriminating respondent will be captured in one of the three intervals, and, assigning n to the total number of discriminating respondents, it is clear that .
.
The ratios,  , may be reclassified by interval, so that there are
, may be reclassified by interval, so that there are  ratios in the range
ratios in the range  to
to 
 (11)
(11)
Since the distribution is uniform over each interval, the expected value for any observation in the interval is the mid-point:
 (12)
(12)
Meanwhile the variance is given by (see e.g. [26] )
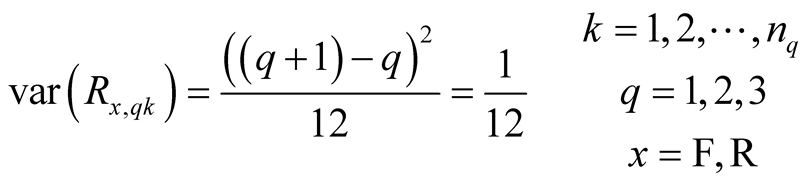 (13)
(13)
These theoretical values are the true mean and the true variance, given that the distribution within each interval is Uniform. This allows the methods of Appendix B to be used to find the expected value and the variance of the combined distribution that constitutes the Piecewise Uniform Distribution.
While the Piecewise Uniform Distribution applies to those respondents who give MAP ratios greater than unity, it is possible to add in those with Type 1 indiscrimination, whose MAP ratio is 1.0. The methods of Appendix B may be used to include this deterministic component, for which  and
and , to produce the Extended Piecewise Uniform Distribution, which covers all computable MAP ratios.
, to produce the Extended Piecewise Uniform Distribution, which covers all computable MAP ratios.
8. Expected MAP Ratios for Discriminating Respondents Based on the Piecewise Uniform Distribution
The calculations outlined in Section 7 have been applied to each of the cohorts and the combined cohort for both Phase 1 and Phase 2. Table 7 shows the expected values for  and
and , while Table 8 shows the standard errors and standard deviations. Table 9 contains the 90% confidence intervals, and shows that the RUP-predicted value of 2.0 lies within this interval for each of the cohorts, TD and BU for Phase 1 and VA and VF for Phase 2, as well as for both combined cohorts. The means of MAP ratios for the discriminating respondents lie close to the theoretical value of 2.0 for each of the two cohorts in each of Phases 1 and 2, with the greatest disparity, just over 10%, occurring for the BU cohort in Phase 1 and the VF cohort in Phase 2. The number of respondents in these cases is, of course, low, at 21 and 17 respectively.
, while Table 8 shows the standard errors and standard deviations. Table 9 contains the 90% confidence intervals, and shows that the RUP-predicted value of 2.0 lies within this interval for each of the cohorts, TD and BU for Phase 1 and VA and VF for Phase 2, as well as for both combined cohorts. The means of MAP ratios for the discriminating respondents lie close to the theoretical value of 2.0 for each of the two cohorts in each of Phases 1 and 2, with the greatest disparity, just over 10%, occurring for the BU cohort in Phase 1 and the VF cohort in Phase 2. The number of respondents in these cases is, of course, low, at 21 and 17 respectively.
The mean for all the discriminating respondents in Phase 1 is 1.98, while the mean for all the discriminating respondents in Phase 2 is 1.93. The 90% confidence interval is 1.77 - 2.18 for Phase 1 and 1.73 - 2.14 for Phase 2. It will be seen that these results conform closely to the prediction of Relative Utility Pricing theory that the MAP ratio will be 2.0.
9. Modeling the MAP Ratio Using a Truncated Lognormal Distribution for All Computable MAP Ratios
As an alternative to the Extended Piecewise Uniform distribution, it is possible also to model all computable MAP ratios using a lognormal distribution, truncated so that the cumulative probabilities below 1.0 and above 4.0 are converted into point values. The probability that the MAP ratio is unity is then the cumulative probability of a MAP ratio up to and including unity, with a similar procedure applied to MAP ratios of 4 and above. When applying the Truncated Lognormal distribution to the combined cohorts of Phase 1 and Phase 2, it is clearly necessary to work with computable MAP ratios. This poses no problems for Phase 2, where the MAP ratio is

Table 7 . Expected MAP ratios for discriminating respondents in the combined and split cohorts for Phase 1 and Phase 2. Piecewise Uniform distribution with numbers in each interval equal to those recorded.

Table 8. Standard errors (s.e) and standard deviations (s.d.) for the combined and split cohorts for Phase 1 and Phase 2, discriminating respondents.

Table 9. 90% confidence intervals for the combined and split cohorts for Phase 1 and Phase 2, discriminating respondents.
computable for all 52 respondents. But in the case of Phase 1, the requirement for computability of MAP ratios means limiting the matching and comparison process to the 67 computable MAP ratios coming from the 81 respondents.
The mean and the standard deviation may be found by minimizing the chi-squared statistic for the Truncated Lognormal distribution. Since the data for Phase 1 are given in 4 cells, one degree of freedom is left for evaluating the p-value. The optimal values are found as  and
and . See Table 10. The associated p-value is 0.095, a figure found after applying the continuity correction of 0.5 necessary when there is just one degree of freedom [27] . Thus when applied to Phase 1, the Truncated Lognormal distribution for RF satisfies comfortably the requirement conventionally required for goodness of fit, namely that the probability of the observed mismatch between the model-predicted number of ratios shown in Table 10 and the recorded numbers should be no less than 0.05.
. See Table 10. The associated p-value is 0.095, a figure found after applying the continuity correction of 0.5 necessary when there is just one degree of freedom [27] . Thus when applied to Phase 1, the Truncated Lognormal distribution for RF satisfies comfortably the requirement conventionally required for goodness of fit, namely that the probability of the observed mismatch between the model-predicted number of ratios shown in Table 10 and the recorded numbers should be no less than 0.05.
In the case of Phase 2, the smaller number of respondents means that ensuring that the predicted number in each cell is at least 5 requires the final two cells to be combined, leaving just 3 cells against which to make comparisons. This number is insufficient to provide any degrees of freedom for a chi-squared test when an optimal matching exercise is to be used to determine the two distribution parameters. However adopting the Truncated Lognormal distribution from Phase 1 allows its predictions to be tested against Phase 2 data, since there are now two degrees of freedom left over. The resultant p-value is then found to be 0.707. This suggests that modeling Phase 2 MAP ratios using the distribution found from Phase 1 is quite satisfactory. See Table 11.
The cut-offs at either end of the Truncated Lognormal distribution render difficult if not impossible the task of finding analytically the expected value,  , of the MAP ratio for the 44 discriminating respondents of Phase 1. But no such difficulty arises if simulation is used to estimate such a value. Singling out the MAP ratios of those with
, of the MAP ratio for the 44 discriminating respondents of Phase 1. But no such difficulty arises if simulation is used to estimate such a value. Singling out the MAP ratios of those with  in the simulation produces average values for discriminating respondents of:
in the simulation produces average values for discriminating respondents of:
 (14)
(14)
with a standard error of estimation of 0.009 and
p-value = 0.095.

Table 12. Medians for the combined cohorts, Phases 1 and 2, based on a lognormal distribution with the same mean and standard deviation.
p-value = 0.707.
 (15)
(15)
with a standard error of estimation of 0.01, based on 200 simulations of cohorts of 67. The average number of discriminating respondents is 43.2, which may be used to estimate that the standard error associated with the average value of  in such a population is about 0.11.
in such a population is about 0.11.
The figures contained in Equations (14) and (15) are similar to those for the discriminating Phase 1 respondents found when a Piecewise Uniform distribution is used (see Table 7 and Table 8). Likewise, the mean and standard deviation resulting for MAP ratios based on the Truncated Lognormal distribution are close to the parameters found for Phase 2 using the Piecewise Uniform distribution for MAP ratio.
The good match provided for the MAP ratios for Phases 1 and 2 suggests that the Truncated Lognormal distribution should be applicable to any group of individuals asked to value safety pack 1 and a safety pack 2 that is three times bigger when those individuals are being pushed close to their limits of discrimination. The Truncated Lognormal distribution may, indeed, be regarded as a more general model for MAP ratio than the Extended Piecewise Uniform distribution, since it avoids the need to specify the numbers of respondents in each cell. The verification by chi-squared tests that the same Truncated Lognormal distribution is able to represent both Phase 1 and Phase 2 MAP ratios provides further corroboration for the claim of increased generality.
The implication is that the precise distribution of the MAP ratios within each MAP-ratio interval is not important. Specifically, it is not necessary that the distributions should be uniform within each interval, 1 - 2, 2 - 3 and 3 - 4, as assumed in the Piecewise Uniform model. The confirmation of the prediction, based on the RUP model, that the mean of the MAP ratio will be about 2.0 is shown to be insensitive to the precise distribution of MAP ratios within each interval.
10. Validation of the Distributions for MAP Ratio by Embedding Them within a Model for the Complete Opinion Survey
A major objective of the paper has now been achieved, namely a demonstration that the MAP ratios for safety packs 1 and 2, which the authors of the Caveat Investigator study regarded as “aberrant”, are fully explicable when it is realized that (i) many respondents are being asked to make judgments beyond their limits for discrimination and (ii) the RUP model will apply to the discriminating respondents.
This section shows that, even though only summary data are available on the respondents’ valuations of safety packs 1 and 2, it is still possible to produce useful simulations of both Phase 1 and Phase 2 opinion surveys. This is because the observed valuations, 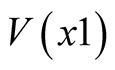 and
and ,
, 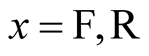 , all obey an approximately lognormal distribution. This is revealed by the close correspondence between the recorded median and the median found from a lognormal distribution in which the recorded mean and the recorded standard deviation are used as parameters. See Table 12.
, all obey an approximately lognormal distribution. This is revealed by the close correspondence between the recorded median and the median found from a lognormal distribution in which the recorded mean and the recorded standard deviation are used as parameters. See Table 12.
Appendix C details the way in which the Extended Piecewise Uniform distribution can be embedded in a simulation that takes the individuals’ valuations of safety pack 1,  ,
,  , as inputs and multiplies these by the individuals’ MAP ratios,
, as inputs and multiplies these by the individuals’ MAP ratios,  ,
,  , to produce valuations of safety pack 2,
, to produce valuations of safety pack 2,  ,
,  , as outputs. The responses of the 14 respondents in Phase 1 who suffer from Type 2 or Type 3 indiscrimination need to be removed because their MAP ratio is not computable, and this may be done using the method explained in Appendix A. Conditioning the Phase 1 valuations,
, as outputs. The responses of the 14 respondents in Phase 1 who suffer from Type 2 or Type 3 indiscrimination need to be removed because their MAP ratio is not computable, and this may be done using the method explained in Appendix A. Conditioning the Phase 1 valuations,  and
and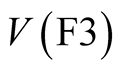 , in this way results in the mean and standard deviations shown in Table 13 for all computable ratios,
, in this way results in the mean and standard deviations shown in Table 13 for all computable ratios,  ,
,  to 67. Table 14 gives the expected values and standard deviations of the computable MAP ratios,
to 67. Table 14 gives the expected values and standard deviations of the computable MAP ratios, 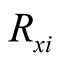 ,
,  , for the comb
, for the comb

Table 13. Phase 1: observed values, conditioned by the removal of zero valuations.

Table 14. Expected values and standard deviations for MAP ratios,  ,
,  , for Phase 1 and Phase 2, all computable ratios; Extended Piecewise Uniform distribution assumed.
, for Phase 1 and Phase 2, all computable ratios; Extended Piecewise Uniform distribution assumed.

Table 15. Phase 1: mean and standard deviation for :
: ; estimation standard errors for simulated average in brackets. Extended Piecewise Uniform distribution for MAP ratio.
; estimation standard errors for simulated average in brackets. Extended Piecewise Uniform distribution for MAP ratio.
ined cohorts under both Phase 1 and Phase 2.
The mean and standard deviation of the output valuation,  ,
,  , may be found either by simulation or analytically. The methods of Appendix E are used in the latter case. Table 15 shows the mean and standard deviation of
, may be found either by simulation or analytically. The methods of Appendix E are used in the latter case. Table 15 shows the mean and standard deviation of 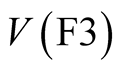 found analytically and by simulation, and compares these values with the conditioned observed values for
found analytically and by simulation, and compares these values with the conditioned observed values for  when the Extended Piecewise Uniform distribution is used to model Phase 1 MAP ratio,
when the Extended Piecewise Uniform distribution is used to model Phase 1 MAP ratio, . Table 16 gives equivalent values for the output valuation,
. Table 16 gives equivalent values for the output valuation,  , under Phase 2.
, under Phase 2.
Table 17 and Table 18 show the average values for mean and standard deviation for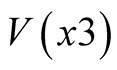 ,
,  , based on 200 simulations, and compare these with the conditioned observed values for Phase 1 and the observed values for Phase 2 when the Truncated Lognormal distribution is used to model MAP ratios.
, based on 200 simulations, and compare these with the conditioned observed values for Phase 1 and the observed values for Phase 2 when the Truncated Lognormal distribution is used to model MAP ratios.
Graphical summaries of the results are provided in Figures 1-4, where the models’ predictions for the number of respondents giving valuations for safety pack 2 within specified intervals are compared with estimates based on the recorded mean and standard deviation. It is clear from Figures 1-4 that the models produce good matches to the summary data on observed values, as discussed at greater length in Appendices C and D. Since these models incorporate the probability distributions for MAP ratio that have been described in Sections 7 and 9, this implies a validation of these probability distributions and thus of their predictions for a mean MAP ratio that lies close to the theoretical value of 2.0 for discriminating respondents.
11. Values for the VPFs
For Phase 1, the authors of the Caveat Investigator study explain the calculation of the VPF:
“Suppose that an individual indicates that her willingness to pay for a 3 in 100,000 reduction in the risk of death in a road traffic accident during the forthcoming year is . That individual’s marginal rate of substitution (MRS) of wealth for risk of death in a road traffic accident would then be well-approximated by
. That individual’s marginal rate of substitution (MRS) of wealth for risk of death in a road traffic accident would then be well-approximated by . It can be shown that the VOSL is then given by the population mean of these individual MRS.”
. It can be shown that the VOSL is then given by the population mean of these individual MRS.”
Since  for any
for any , it follows that the VPFs for Phase 1 may be found by dividing the mean of
, it follows that the VPFs for Phase 1 may be found by dividing the mean of  by
by 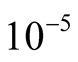 and the mean of
and the mean of  by
by .
.
Meanwhile for Phase 2 the authors recommend:
“It is most straightforward to proceed by multiplying the mean household willingness to pay by the number of households in the area affected (i.e. 400,000) and then dividing the result by the number of fatalities prevented by the safety program concerned.”
Hence the VPFs for Phase 2 may be found by multiplying the mean of  by 400,000 then dividing the result by 5 and by multiplying the mean of
by 400,000 then dividing the result by 5 and by multiplying the mean of  by 400,000 then dividing the result by 15. (This procedure assumes that the monetary values placed on the 5 year safety programmes of VF have already been divided by 5 to produce annualized equivalents. See note to Table 3 and Table 4 in Section 3).
by 400,000 then dividing the result by 15. (This procedure assumes that the monetary values placed on the 5 year safety programmes of VF have already been divided by 5 to produce annualized equivalents. See note to Table 3 and Table 4 in Section 3).

Table 16. Phase 2: mean and standard deviation for :
: ; estimation standard errors for simulated average in brackets. Extended Piecewise Uniform distribution for MAP ratio.
; estimation standard errors for simulated average in brackets. Extended Piecewise Uniform distribution for MAP ratio.

Table 17. Phase 1: mean and standard deviation for :
: ; estimation standard errors for simulated average in brackets. Truncated Lognormal distribution for MAP ratio.
; estimation standard errors for simulated average in brackets. Truncated Lognormal distribution for MAP ratio.

Table 18. Phase 2: mean and standard deviation for :
: ; estimation standard errors for simulated average in brackets. Truncated Lognormal distribution for MAP ratio.
; estimation standard errors for simulated average in brackets. Truncated Lognormal distribution for MAP ratio.

Figure 1. Number of responses in £50 intervals for : observed distribution, distribution with parameters from Table 15 (both assumed lognormal) and distribution from a simulated cohort of 67; Extended Piecewise Uniform distribution for MAP ratio.
: observed distribution, distribution with parameters from Table 15 (both assumed lognormal) and distribution from a simulated cohort of 67; Extended Piecewise Uniform distribution for MAP ratio.

Figure 2. Number of responses in £25 intervals for : observed distribution, distribution with parameters from Table 16 (both assumed lognormal) and distribution from a simulated cohort of 52; Extended Piecewise Uniform distribution for MAP ratio.
: observed distribution, distribution with parameters from Table 16 (both assumed lognormal) and distribution from a simulated cohort of 52; Extended Piecewise Uniform distribution for MAP ratio.

Figure 3. Number of responses in £50 intervals for : observed distribution, distribution with parameters from Table 17 (both assumed lognormal) and distribution from a simulated cohort; Truncated Lognormal distribution for MAP ratio.
: observed distribution, distribution with parameters from Table 17 (both assumed lognormal) and distribution from a simulated cohort; Truncated Lognormal distribution for MAP ratio.

Figure 4. Number of responses in £25 intervals for : observed distribution, distribution with parameters from Table 18 (both assumed lognormal) and distribution from a simulated cohort; Truncated Lognormal distribution for MAP ratio.
: observed distribution, distribution with parameters from Table 18 (both assumed lognormal) and distribution from a simulated cohort; Truncated Lognormal distribution for MAP ratio.

Table 19. VPF values (1997 £M); safety pack 2 offers three times the safety benefit offered by safety pack 1. The simulation values are averages over 200 cohorts of respondents.
The resulting values for the VPFs are VPF1 = £9.83 M and VPF2 = £4.63 M under Phase 1 while VPF1 = £8.70 M and VPF2 = £3.87 M under Phase 2, as reported by the authors of the Caveat Investigator study. Here VPF1 is derived from safety pack 1 while VPF2 is derived from safety pack 2.
All observed MAP ratios are computable in Phase 2 and so it is possible to derive VPF figures immediately using the simulation models described in Section 10. Table 19 lists the resulting average values over 200 cohorts each containing 52 respondents: VPF1 = £8.75 M and VPF2 = £4.49 M when the Extended Piecewise Uniform distribution is used, and VPF1 = £8.61 M and VPF2 = £4.68 M when the Truncated Lognormal distribution is used.
Clearly the general trend is captured that VPF2 is significantly lower than VPF1. Moreover, although the average VPF2 values coming from the simulation are above the recorded value of £3.87 M, there is an estimated 21% chance of the simulated VPF2 being at or below £3.87 M (43 out of 200 simulations under the Extended Piecewise Uniform distribution, 42 out of 200 simulations under the Truncated Lognormal). Figure 5 gives an indication of the distribution of VPF2 values based on use of the Extended Piecewise Uniform distribution.
However, the inclusion of the VPF values for respondents who are unable to discriminate the benefits of one or the other safety pack or else between the two safety packs causes the figures for VPF to be biased low. Conditioning the observed valuations for safety pack [F1] by removing the zero valuations assigned by those with Type 2 or Type 3 indiscrimination increases the VPF1 figure for Phase 1 from £9.83 M to £11.88 M. The methods of Appendix A, based on the schematic of Figure 6 are applied here to effect this removal.
Taking out the valuations of safety pack [F1] made by the respondents with indiscrimination of Types 2 and 3 has the effect of increasing VPF2 under Phase 1 from £4.63 M to £5.24 M. The valuations of those suffering from Type 1 indiscrimination may now be excluded also. Under the assumption that it is only the valuations of [F3] and [R3] that will be affected by Type 1 indiscrimination, and not the valuations of [F1] and [R1], the effect of these exclusions will be seen on VPF2 but not on VPF1. The conditioned, observed value of VPF2 rises to £5.91 M in Phase 1 and to £4.58 M in Phase 2.
Table 19 shows the full list of observed figures, with and without conditioning, as well as the average values based on 200 simulations of the cohorts. (The Extended Piecewise Uniform distribution is equivalent to the Piecewise Uniform distribution when all respondents are discriminating).

Figure 5. Number of cohorts within intervals of VPF2: 200 simulations using Extended Piecewise Uniform distribution for MAP ratio for Phase 2.
The phenomenon has thus been explained whereby significantly different VPF values will arise when people are asked to value an entry-level safety pack and another that offers a greater improvement in safety. However, it is necessary to remove the effects of indiscrimination if the results are to be generalized to situations where the safety improvements are large enough for everyone to discriminate, as might be the case if safety pack 1 offered a reduction in fatal accident frequency of 10−4 rather than 10−5 per person per year or lower.
When the effects of indiscrimination are removed, the evidence from the Caveat Investigator surveys is that people will provide valuations of a life-prolonging safety pack 1 that imply an average value of VPF in the range: £8.70 M ≤ VPF1 ≤ £11.88 M, while their valuations of a second safety pack offering three times the benefits

Figure 6. Flow diagram for calculating sample mean and sample standard deviation of combined sample.
will be in the range: £4.58 M ≤ VPF2 ≤ £5.91 M. The above valuations are generally higher than the figures declared by the Caveat Investigator authors.
The conversion from 1997 £s to 2014 £s requires an increase by a factor of 1.622, so that, in today’s money the figures would be: £14.11 M ≤ VPF1 ≤ £19.27 M and £7.43 M ≤ VPF2 ≤ £9.59 M, between five times and ten times the value in use in the UK today [13] . Since these figures are fully explicable in terms of human preferences, it must be concluded that, if regulators and others wish to be guided by stated preference methods there is no valid justification for rejecting them.
RUP theory suggests that, when offered two safety packs, the second giving n times the benefit of the first, where , the ratio of the MAPs amongst discriminating respondents will be
, the ratio of the MAPs amongst discriminating respondents will be , leading to a ratio of
, leading to a ratio of . This will have a significant effect on the VPF2 value when
. This will have a significant effect on the VPF2 value when  is relatively small, with an individual’s VPF2 being expected to be of the order of 20% lower than his VPF1 when
is relatively small, with an individual’s VPF2 being expected to be of the order of 20% lower than his VPF1 when , for example, reducing to 10% lower when
, for example, reducing to 10% lower when . In general we may deduce that for discriminating respondents:
. In general we may deduce that for discriminating respondents:
 (16)
(16)
with the higher VPF, VPF1, being the limiting value in the sense that  for high
for high . For the case where everyone can discriminate, the RUP model predicts a VPF2 for Phase 1 of £7.92 M (two-thirds of the conditioned observed VPF1 of £11.88 M), a value that is very close to the average simulated values given in the last two lines of Table 19 (£7.71 M and £7.88 M) and comparable with the conditioned observed value of £5.91 M. Similarly for Phase 2, the RUP model predicts a VPF2 of £5.80 M based on the observed value of £8.70 M for VPF1, a figure that is very close to the average simulated values (£5.64 M and £5.70 M) and of a similar size to the conditioned observed value of £4.58 M.
. For the case where everyone can discriminate, the RUP model predicts a VPF2 for Phase 1 of £7.92 M (two-thirds of the conditioned observed VPF1 of £11.88 M), a value that is very close to the average simulated values given in the last two lines of Table 19 (£7.71 M and £7.88 M) and comparable with the conditioned observed value of £5.91 M. Similarly for Phase 2, the RUP model predicts a VPF2 of £5.80 M based on the observed value of £8.70 M for VPF1, a figure that is very close to the average simulated values (£5.64 M and £5.70 M) and of a similar size to the conditioned observed value of £4.58 M.
12. Discussion
The Relative Utility Pricing model has shown that what the authors of the Caveat Investigator study described as “aberrant responses” are actually nothing of the kind. Removing the responses of the people pushed beyond their limits of discrimination and then applying the RUP model makes it clear that the discriminating respondents are valuing different sizes of safety packs in the same way as they would value other commodities offered for sale in supermarkets or on the internet in different pack-sizes. The RUP model predicts that discriminating people, those able both to see a benefit from the smaller safety pack and to discriminate between the two packs, will build a substantial quantity discount into their valuation of a safety pack providing three times the safety benefit offered by the entry-level safety pack. The average ratio of the valuations amongst discriminating respondents is forecast to be 2.0, rather than 3.0 or a value close to it.
This prediction receives robust validation from the data in all of the surveys. Using the Piecewise Uniform distribution to interpret the classified data for MAP ratio, the 90% confidence interval includes the value 2.0 for discriminating respondents in each of the 6 cohorts in the Caveat Investigator study: TD, BU and the combined cohort from Phase 1, as well as VA, VF and the combined cohort from Phase 2.
The standard error reduces and the average valuation ratio approaches closely the theoretical MAP ratio of 2.0 when the larger numbers associated with the combined cohorts are taken into account. Thus the standard error goes down to 0.12 and the average MAP ratio is 1.93 when the Piecewise Uniform distribution is used to interpret the classified data for MAP ratio for Phase 2, which has 30 discriminating respondents. Then for Phase 1, in which there are 44 discriminating respondents, the standard error is 0.13, while the average MAP ratio, at 1.98, has moved to within 1% of the predicted value of 2.0.
An alternative distribution, the Truncated Lognormal, gives a good match to the classified MAP ratio data, as confirmed by the high p-values gained in the associated chi-squared tests. Simulations using this alternative distribution show that the MAP ratio for discriminating respondents has a mean of 1.98 with a standard error of 0.11, thus confirming once more the prediction of the RUP model. Moreover the success of this alternative distribution demonstrates that the confirmation of the RUP prediction is insensitive to the precise distribution of MAP ratios within each classification interval.
Further validation for the Piecewise Uniform and Lognormal distributions for MAP ratio for discriminating correspondents is provided by the simulations of both the Phase 1 survey as a whole and the Phase 2 survey as a whole. The good visual match between the distribution for the simulated valuation of safety pack 2 and the reported distribution, deduced to be approximately lognormal, confirms the two distributions as adequate models for the MAP ratios of the discriminating respondents.
The simulations, broadened out to include respondents with Type 1 indiscrimination, also give an insight to the behavior of the two VPFs, VPF1 and VPF2, that are inevitable when people are asked to state the values they will assign to two safety packs, the larger conferring a low multiple of the benefits of the smaller. Based on an average over all respondents, a simulation of Phase 2 using the Extended Piecewise Uniform distribution for MAP ratio produces VPF1 = £8.75 M and VPF2 = £4.49 M, which may be compared with the recorded results of VPF1 = £8.70 M and VPF2 = £3.87 M. Similar values are produced when the Truncated Lognormal distribution is used. It is clear that the modeling has captured the phenomenon of the two distinct and widely separated VPF modes observed in practice. The average figure for VPF2 from the simulations is within 16% of the observed value and, furthermore, the simulated VPF2 is predicted to be at or below £3.87 M for about 20% of Phase 2 surveys.
The comparison between the simulations and the recorded results for Phase 1 is complicated by the fact that 14 out of the 81 respondents of Phase 1 suffer from the more severe indiscrimination of Types 2 and 3, rendering their MAP ratio incomputable. Removal of the Type 2 and Type 3 responses by the conditioning method of Appendix A leads to conditioned observed VPF values of VPF1 = £11.88 M and VPF2 = £5.24 M, which may be compared with the simulated values of VPF1 = £11.80 M and VPF2 = £6.42 M calculated when the Extended Piecewise distribution for MAP ratio is used, with similar values being produced when the Truncated Lognormal distribution is applied. When all types of indiscrimination are removed, the simulations produce average VPF2 values that are similar to the predictions of RUP theory and of a similar size to the conditioned observed value of VPF2. The phenomenon of two distinct and widely separated VPF modes is correctly predicted.
It is necessary to strip out the effects of indiscrimination to generalize the results, and this leads to higher VPF values. In £s of 2014, VPF1 then lies between £14.11 M and £19.27 M, while VPF2 is between £7.43 M and £9.59 M. RUP theory suggests that VPF2 will converge to the larger VPF1 when safety pack 2 offers safety benefits that are very much higher than those offered by safety pack 1, which asymptotic behavior might mark out the higher VPF1 as having more general applicability.
There would appear to be no valid reason for dismissing the VPFs listed if the decision is taken to follow the stated preference route for valuing human life. Far from being caused by “a number of theoretically irrelevant factors”, as claimed by the Caveat Investigator authors, the two VPF figures, VPF1 and VPF2, have been explained fully in terms of economic theory. While the fact that these VPF values are up to an order of magnitude greater than the VPF currently in use might constitute an inconvenience, that in itself can hardly justify a rejection of these values by those committed to stated preference methods.
The difficulty remains, of course, that opinion surveys will tend to provide a significantly different VPF figure depending on the size of the safety benefit. No unique figure for VPF can be expected when stated preference techniques are used.
13. Conclusions
Two distinct and widely separated VPF figures, VPF1 associated with safety pack 1 and VPF2 associated with safety pack 2 are the inevitable outcome of any survey that asks people to value two safety packs, where the larger one confers a safety benefit that is a low multiple of that conferred by the smaller safety pack.
The basic mechanism underlying the two, markedly different VPFs, is Relative Utility Pricing. By the RUP model, people assigning their MAPs to two packs of a commodity, with the second pack being  times larger than the first, will put a valuation on the larger pack that is only
times larger than the first, will put a valuation on the larger pack that is only  times greater than the value they put on the smaller pack.
times greater than the value they put on the smaller pack.
In the case of the Caveat Investigator study, where safety pack 2 confers three times the benefit of safety pack 1, the MAP ratio is predicted to be 2.0, and this figure has been confirmed by the behavior of the discriminating respondents, to whom RUP applies. Their MAP ratios have been found to average between 1.93 and 1.98, with 2.0 included in the 90% confidence intervals.
Simulation models, broadened to include not only discriminating respondents conforming to RUP but also respondents with Type 1 indiscrimination, have reproduced approximately the two very different VPF values found from the views of all the respondents in Phase 2 of the Caveat Investigator study. Similar results were produced for Phase 1, although in that case it was necessary to condition the observations to remove the effect of those who set a zero value on safety pack 1, namely those suffering from Type 2 or Type 3 indiscrimination.
It may be concluded that there is no inconsistency in the VPF results reported in the Caveat Investigator study, despite the fact that they were dismissed by its authors.
The VPF values for general use need to be modified if they are to be applied to situations where the safety benefits are large enough for everyone to discriminate. Stripping out the effects of indiscrimination leads to a VPF1 of between £14.11 M and £19.27 M, and a VPF2 that lies between £7.43 M and £9.59 M (2014 £s).
By RUP theory, the lower VPF2 will converge to the larger VPF1 when safety pack 2 offers safety benefits that are very much higher than those offered by safety pack 1. This asymptotic behavior marks out the higher VPF1 as having more general applicability.
Since the VPF figures observed can be explained fully in terms of economic theory, there is clearly no valid reason for dismissing the VPFs above if the stated preference route is chosen as the vehicle for valuing human life unless the Caveat Investigator study contains a fault or faults yet to be revealed. It is true that the VPF values found in the study are up to an order of magnitude greater than the VPF currently in use in the UK today, but while this might constitute an inconvenience that can hardly justify a rejection of these values by those who are committed to stated preference methods.
As noted in the Introduction, however, there are reasons for viewing stated preference techniques with caution, as there will always be doubts on whether the person’s stated valuation will conform to what he will actually be prepared to pay. Moreover, the whole concept of a unique figure for VPF of general applicability has been shown to be incompatible with the use of stated preference techniques. It is thus apparent that there are significant difficulties in the interpretation of surveys to establish a VPF. This has been shown not only here but also by the demonstrated invalidity of the two-injury chained method, which was advanced by the Caveat Investigator team as a notional replacement for their initial opinion surveys.
The problems and confusions associated with the current, stated preference approaches for assessing how much to spend to safeguard human life mean that there is a pressing and unfulfilled need to ensure adequate protection for UK public and workers from industrial and transport hazards. A re-appraisal is urgently required of methodologies, such as J-value, that are based on the surer ground of revealed preferences, and can allow robust decision making on safety by industry and the regulatory authorities.
Acknowledgements
The authors wish to thank Mr. Roger Jones, Visiting Fellow at City University London, for his assistance and advice during the preparation of this paper.
Part of the work reported on was carried out for the NREFS project, Management of Nuclear Risk Issues: Environmental, Financial and Safety, led by City University London in collaboration with Manchester, Warwick and The Open Universities and with the support of the Atomic Energy Commission of India as part of the UK-India Civil Nuclear Power Collaboration. The authors acknowledge gratefully the support of the Engineering and Physical Sciences Research Council (EPSRC) under grant reference number EP/K007580/1. The views expressed in the paper are those of the authors and not necessarily those of the NREFS project.
Appendix A. Characteristics of a Sample Taken from Several Distributions
A.1 Finding the Sample Mean
The scheme for combining the statistics of the records is given diagrammatically in Figure 6. Let there be a sample that combines  records taken from a distribution with an estimated mean,
records taken from a distribution with an estimated mean,  , and an estimated variance,
, and an estimated variance,  , and
, and  records taken from a distribution with an estimated mean,
records taken from a distribution with an estimated mean,  , and an estimated variance,
, and an estimated variance, . The combined sample will thus have
. The combined sample will thus have  records.
records.
Let the sample mean of the combined sample be denoted  and its sample variance,
and its sample variance, . The sample mean will be given by:
. The sample mean will be given by:
 (A.1)
(A.1)
where ;
;  are the sample values taken from the first distribution and
are the sample values taken from the first distribution and ;
;  are the sample values taken from the second distribution. Now
are the sample values taken from the second distribution. Now
 (A.2)
(A.2)
where  is the mean of the values contained in the combined sample but taken from the first distribution. Similarly
is the mean of the values contained in the combined sample but taken from the first distribution. Similarly
 (A.3)
(A.3)
where  is the mean of the values contained in the combined sample but taken from the second distribution. Hence the sample mean of the combined sample will be
is the mean of the values contained in the combined sample but taken from the second distribution. Hence the sample mean of the combined sample will be
 (A.4)
(A.4)
If the sample is taken from three distributions, then simple extensions of Equations (A.1) to (A.4) give the new sample mean of the extended sample,  , as:
, as:
 (A.5)
(A.5)
where the subscript, 3, denotes the third distribution and the total number of records is now
 . Equation (A.5) may be recast as:
. Equation (A.5) may be recast as:
 (A.6)
(A.6)
Equation (A.6) may now be generalized to account for records being taken from k distributions, when the overall sample mean will be , given by:
, given by:
 (A.7)
(A.7)
A.2 The Sample Variance
For a set of  randomly drawn records,
randomly drawn records,  , with sample mean,
, with sample mean,
 (A.8)
(A.8)
the unbiased sample variance,  , may be written:
, may be written:
 (A.9)
(A.9)
where Equation (A.8) has been used in the penultimate step. Hence, using the notation employed above, the sample variance,  , of a combined sample drawn from two distributions will obey:
, of a combined sample drawn from two distributions will obey:
 (A.10)
(A.10)
where Equation (A.4) has been used in the second step. But we may define the sample variance,  , by:
, by:
 (A.11)
(A.11)
and the sample variance,  , by:
, by:
 (A.12)
(A.12)
Therefore:
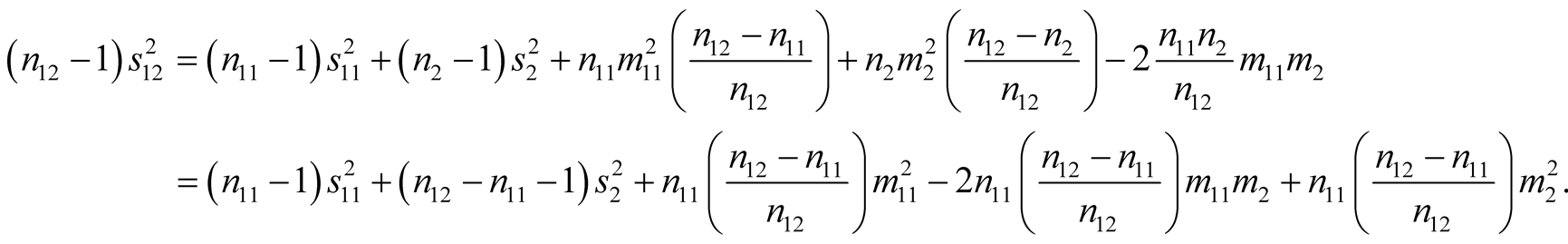 (A.13)
(A.13)
Noting that 
 (A.14)
(A.14)
Thus the sample variance,  , of a combined sample taken from two distributions is:
, of a combined sample taken from two distributions is:
 (A.15)
(A.15)
For the general case where the sample is drawn from k distributions, Equation (A.15) becomes:
 (A.16)
(A.16)
Equations (A.7) and (A.16) may be applied successively with  then
then  and so on until all the distributions have been included. See Figure 6.
and so on until all the distributions have been included. See Figure 6.
A.3 Removing a Component Distribution from the Combined Sample
The starting point for the treatment above is that the characteristics of the component distributions are known and the aim is to characterize the combined sample. There may be occasions, however, when the characteristics of the combined sample are known, at least approximately, as well as those of one of the component distributions. The following treatment applies when estimates of mean and variance are available for the combined sample and for distribution 2 and it is necessary to estimate the sample mean,  , and sample variance,
, and sample variance,  , of the distribution identified with the subscript, “11”, in Figure 6.
, of the distribution identified with the subscript, “11”, in Figure 6.
Rearrangement of Equation (A.4) gives:
 (A.17)
(A.17)
Meanwhile, from Equation (A.15):
 (A.18)
(A.18)
The calculation relies on the use of the estimated means and variances:
 (A.19)
(A.19)
Appendix B. Characteristics of a Cohort Involving Several Distributions for Each of Which the Population Mean and Population Variance Are Known Exactly
A method that parallels the development of Appendix A is presented for the case where the population mean and variance are known rather than estimates. An alternative method based on the same principles is presented in Section B.3.
B.1 Finding the Mean of the Combined Cohort
The general outline of Figure 6 is followed once again, but now with  and
and  replacing
replacing  and
and  respectively. Let there be a cohort that combines
respectively. Let there be a cohort that combines  records,
records,  , taken from a distribution with a true mean,
, taken from a distribution with a true mean,  , and a true variance,
, and a true variance,  , and
, and  records,
records,  , taken from a distribution, with a true mean,
, taken from a distribution, with a true mean,  , and a true variance,
, and a true variance, . The combined cohort will thus have
. The combined cohort will thus have  records,
records,  , with a population mean,
, with a population mean,  , and population variance,
, and population variance, .
.
If a record,  , is chosen at random from the combined cohort, its expected value will depend on whether the record comes originally from the “11” distribution or from the “2” distribution. Define a random variable,
, is chosen at random from the combined cohort, its expected value will depend on whether the record comes originally from the “11” distribution or from the “2” distribution. Define a random variable,  , as an indicator variable that takes the values:
, as an indicator variable that takes the values:
 (B.1)
(B.1)
It follows that
 (B.2)
(B.2)
 (B.3)
(B.3)
The expected value of a record in the combined cohort,  is then:
is then:
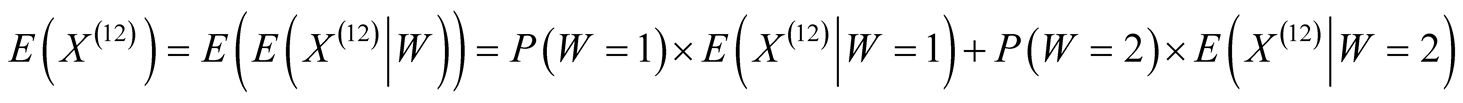 (B.4)
(B.4)
The probability of choosing a record originally from distribution “11” is , while the probability of choosing a record originally from distribution “2” is
, while the probability of choosing a record originally from distribution “2” is . On substituting these values into Equation (B.4) and also using Equations (B.2) and (B.3), it is found that:
. On substituting these values into Equation (B.4) and also using Equations (B.2) and (B.3), it is found that:
 (B.5)
(B.5)
or, in more compact notation:
 (B.6)
(B.6)
If the cohort is taken from three distributions, then simple extensions of Equations (B.1) to (B.5) give the new population mean of the combined cohort,  , as:
, as:
 (B.7)
(B.7)
where the subscript, 3, denotes the third distribution and the total number of records is now  . Equation (B.7) may be recast as:
. Equation (B.7) may be recast as:
 (B.8)
(B.8)
Equation (B.8) may now be generalized to account for records being taken from  distributions, when the true mean will be
distributions, when the true mean will be , given by:
, given by:
 (B.9)
(B.9)
B.2 Population Variance for the Combined Cohort
The population variance,  , may be written:
, may be written:
 (B.10)
(B.10)
The principles outlined in Section B.1 can be applied not only to the expectation of  but also to its square,
but also to its square, . Hence, by direct analogy with Equation (B.5):
. Hence, by direct analogy with Equation (B.5):
 (B.11)
(B.11)
Substituting from Equation (B.11) into Equation (B.10) gives:
 (B.12)
(B.12)
which may then be developed as follows:
 (B.13)
(B.13)
where Equation (B.6) has been used in the second line. But, since :
:
 (B.14)
(B.14)
or
 (B.15)
(B.15)
Generalizing, the effect on the population of selecting from  distributions is:
distributions is:
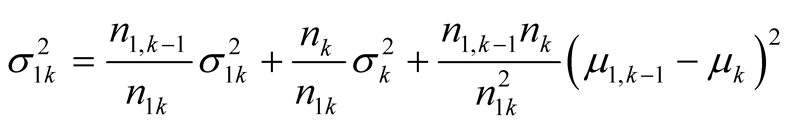 (B.16)
(B.16)
B.3 Alternative Form
An alternative continuation is possible after Equation (B.12), which may be written:
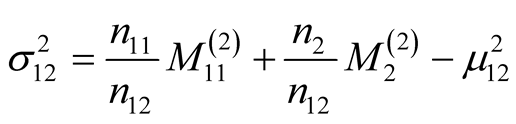 (B.17)
(B.17)
where ,
,  are the second moments about the origin for the distributions identified by the subscripts, “11” and “2”. Changing the notation so that the distributions to be combined are numbered
are the second moments about the origin for the distributions identified by the subscripts, “11” and “2”. Changing the notation so that the distributions to be combined are numbered , Equation (B.17) may be generalized to give the population variance when all N distributions are combined:
, Equation (B.17) may be generalized to give the population variance when all N distributions are combined:
 (B.18)
(B.18)
where
 (B.19)
(B.19)
Appendix C. Validation of the Results of the Extended Piecewise Uniform Distribution Model
The validation exercise is applied to combined cohorts from each of Phase 1 and Phase 2, giving the benefit of working with larger numbers. This avoids also the problem, explained in the note to Table 5, of lack of information on the distribution of the zero responses between the TD and BU cohorts.
In spite of the limited data available, corroboration for the results of the Extended Piecewise Uniform distribution for the MAP ratio may be achieved by embedding this distribution within an input-output model, where the individual’s valuation,  ,
,  , is the input and the valuation,
, is the input and the valuation, 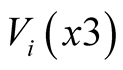 ,
,  , is the output produced by multiplying by the individual’s MAP ratio,
, is the output produced by multiplying by the individual’s MAP ratio, :
:
 (C.1)
(C.1)
A lognormal model for ,
,  may be used because of the approximately lognormal relationship found to exist in the observed valuations of [F1] and [R1], as revealed by the correspondence between the recorded median and that resulting from a lognormal distribution with the recorded mean and standard deviation as parameters. As shown in Table 12,
may be used because of the approximately lognormal relationship found to exist in the observed valuations of [F1] and [R1], as revealed by the correspondence between the recorded median and that resulting from a lognormal distribution with the recorded mean and standard deviation as parameters. As shown in Table 12,  ,
,  may be considered to obey a lognormal distribution by the same token.
may be considered to obey a lognormal distribution by the same token.
The useful application of Equation (C.1) requires, of course, that the ratio,  ,
,  , should exist. This requirement is satisfied for all the respondents in Phase 2, but in Phase 1 there are 14 cases of indiscrimination of either Type 2 or Type 3, where the respondent values
, should exist. This requirement is satisfied for all the respondents in Phase 2, but in Phase 1 there are 14 cases of indiscrimination of either Type 2 or Type 3, where the respondent values  as zero, and assigns
as zero, and assigns  either a positive value (Type 2 indiscrimination: 6 respondents) or zero (Type 3 indiscrimination: 8 respondents). The MAP ratio,
either a positive value (Type 2 indiscrimination: 6 respondents) or zero (Type 3 indiscrimination: 8 respondents). The MAP ratio,  is rendered indeterminate in these 14 instances, making it necessary to filter out the effects of these 14 respondents to produce conditioned observed distributions for
is rendered indeterminate in these 14 instances, making it necessary to filter out the effects of these 14 respondents to produce conditioned observed distributions for 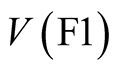 and
and .
.
C.1 Removing the Zero Responses from the Phase 1 Valuation Distributions (Types 2 and 3 Indiscrimination)
The 14 zero responses inherent in the observed distribution for  may be removed easily, since the mean and standard deviation of the set of zero valuations are both zero. Applying the method of Section A.3 of Appendix A, the resultant mean of the 67 remaining valuations,
may be removed easily, since the mean and standard deviation of the set of zero valuations are both zero. Applying the method of Section A.3 of Appendix A, the resultant mean of the 67 remaining valuations,  , rises by about £20 to £118.79, while the standard deviation for those 67 valuations of [F1] is now £148.44. The 8 zero responses inherent in the observed distribution for
, rises by about £20 to £118.79, while the standard deviation for those 67 valuations of [F1] is now £148.44. The 8 zero responses inherent in the observed distribution for  may be treated in the same way and this results in a mean of £154.12 for the remaining 73 valuations of the safety pack, [F3], and a standard deviation of £181.50.
may be treated in the same way and this results in a mean of £154.12 for the remaining 73 valuations of the safety pack, [F3], and a standard deviation of £181.50.
It is necessary also to remove from the distribution for  the effect of the valuations from the six respondents suffering from Type 2 indiscrimination. It is assumed first that the value placed on safety pack 1,
the effect of the valuations from the six respondents suffering from Type 2 indiscrimination. It is assumed first that the value placed on safety pack 1,  , by respondents with Type 1 indiscrimination will be generally similar to those of the discriminating respondents, and hence that their distribution for
, by respondents with Type 1 indiscrimination will be generally similar to those of the discriminating respondents, and hence that their distribution for  will have a mean and a standard deviation the same as those just found for the 67 respondents just discussed, namely £118.79 and £148.44 respectively. The additional assumption is now made that the distribution for
will have a mean and a standard deviation the same as those just found for the 67 respondents just discussed, namely £118.79 and £148.44 respectively. The additional assumption is now made that the distribution for , for those with Type 2 indiscrimination matches the distribution for
, for those with Type 2 indiscrimination matches the distribution for  of respondents suffering from the less severe Type 1 indiscrimination. Since those with Type 1 indiscrimination place the same value on safety pack 2 as for safety pack 1, so that
of respondents suffering from the less severe Type 1 indiscrimination. Since those with Type 1 indiscrimination place the same value on safety pack 2 as for safety pack 1, so that , it follows that the distribution for
, it follows that the distribution for  amongst those with Type 2 indiscrimination will have a mean and standard deviation of £118.79 and £148.44 respectively. Removing the effect of the six valuations with these characteristic parameters produces a final distribution for the valuation of [F3] among the 67 respondents who are discriminating or suffer from Type 1 indiscrimination that is characterized by a mean of £157.29 and a standard deviation of £184.78. The results are summarized in Table 13.
amongst those with Type 2 indiscrimination will have a mean and standard deviation of £118.79 and £148.44 respectively. Removing the effect of the six valuations with these characteristic parameters produces a final distribution for the valuation of [F3] among the 67 respondents who are discriminating or suffer from Type 1 indiscrimination that is characterized by a mean of £157.29 and a standard deviation of £184.78. The results are summarized in Table 13.
The parameters for the conditioned, observed distribution  are, in fact, relatively insensitive to the parameters for
are, in fact, relatively insensitive to the parameters for  assumed for those with Type 2 indiscrimination. As an example, reducing by a factor of two the mean and standard deviation of the valuation of [F3] on the part of the 6 respondents with Type 2 indiscrimination increases the conditioned observed values to £162.60 and £186.09 respectively.
assumed for those with Type 2 indiscrimination. As an example, reducing by a factor of two the mean and standard deviation of the valuation of [F3] on the part of the 6 respondents with Type 2 indiscrimination increases the conditioned observed values to £162.60 and £186.09 respectively.
C.2 Modeling the Output Distribution for V(F3) in Phase 1
A single mean and variance for the MAP ratio,  , may be found under the assumption of an Extended Piecewise Uniform distribution for MAP ratio using the methods of Appendix B. See Table 14. The action of the Extended Piecewise Uniform distribution for MAP ratio on the input distribution for
, may be found under the assumption of an Extended Piecewise Uniform distribution for MAP ratio using the methods of Appendix B. See Table 14. The action of the Extended Piecewise Uniform distribution for MAP ratio on the input distribution for  is then modeled using Equations (E.3) and (E.9) from Appendix E to calculate analytically the parameters of the output distribution,
is then modeled using Equations (E.3) and (E.9) from Appendix E to calculate analytically the parameters of the output distribution, .
.
If the valuation, 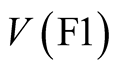 , and the MAP ratio,
, and the MAP ratio,  , are assumed to be independent then the correlation coefficient,
, are assumed to be independent then the correlation coefficient,  , will be zero, and this produces predictions of £195.0 and £262.5 for the mean and standard deviation of
, will be zero, and this produces predictions of £195.0 and £262.5 for the mean and standard deviation of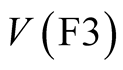 . An exact match with the conditioned observed mean for
. An exact match with the conditioned observed mean for , £157.29, is produced when
, £157.29, is produced when , while the standard deviation is reduced to £248.0. The negative value of
, while the standard deviation is reduced to £248.0. The negative value of  suggests that there may be a negative correlation between input valuation,
suggests that there may be a negative correlation between input valuation,  , and MAP ratio, but that it is very weak:
, and MAP ratio, but that it is very weak: . Hence models based on independence between
. Hence models based on independence between  and
and  are likely to give a reasonable representation of reality.
are likely to give a reasonable representation of reality.
As an alternative, it is possible to simulate numerically the multiplication of sets of two random variables, assumed independent. The assumption is made that the conditioned input valuation,  , with parameters given in Table 13, follows a lognormal distribution in the same way as the original distribution for
, with parameters given in Table 13, follows a lognormal distribution in the same way as the original distribution for . The valuations,
. The valuations,  , of 200 cohorts of 67 people are then simulated, with each being multiplied by a realization of one of the components of the Extended Piecewise Uniform Distribution for MAP ratio. 67 output valuations,
, of 200 cohorts of 67 people are then simulated, with each being multiplied by a realization of one of the components of the Extended Piecewise Uniform Distribution for MAP ratio. 67 output valuations,  , are then produced for each cohort. Cohort averages are then found and these are averaged further over the 200 simulations.
, are then produced for each cohort. Cohort averages are then found and these are averaged further over the 200 simulations.
The results derived under the assumption that  and
and  are independent are shown in Table 15, where they are compared with the conditioned observed values for the 67 respondents who are either discriminating or suffer from Type 1 indiscrimination. Figure 1 illustrates that there is a very close match between the calculations and the distribution for
are independent are shown in Table 15, where they are compared with the conditioned observed values for the 67 respondents who are either discriminating or suffer from Type 1 indiscrimination. Figure 1 illustrates that there is a very close match between the calculations and the distribution for  based on the conditioned observed figures in terms of the numbers found in valuation intervals of £50. Shown are (i) the conditioned observed distribution for
based on the conditioned observed figures in terms of the numbers found in valuation intervals of £50. Shown are (i) the conditioned observed distribution for  among discriminating and Type 1 respondents, assumed lognormal, (ii) one realization of 67 people chosen to have a sample mean and sample standard deviation each close to the figures of Table 15, and (iii) the calculated distribution based on the simulation average figures from Table 15.
among discriminating and Type 1 respondents, assumed lognormal, (ii) one realization of 67 people chosen to have a sample mean and sample standard deviation each close to the figures of Table 15, and (iii) the calculated distribution based on the simulation average figures from Table 15.
Justification for taking the distribution of  after conditioning to be lognormal is provided by the facts that (i) the distribution for the unconditioned version is approximately lognormal, (ii) the distribution for the corresponding valuation,
after conditioning to be lognormal is provided by the facts that (i) the distribution for the unconditioned version is approximately lognormal, (ii) the distribution for the corresponding valuation, 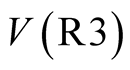 , in Phase 2 (where no conditioning is required) is approximately lognormal and (iii) it is clear from Figure 1 that the simulation’s predicted output distribution for
, in Phase 2 (where no conditioning is required) is approximately lognormal and (iii) it is clear from Figure 1 that the simulation’s predicted output distribution for  is approximately lognormal.
is approximately lognormal.
A further way of judging the proximity of the results to the observation is found by carrying out 1,000 simulations of cohorts of 67 people when it is assumed that the distribution for  is lognormal with a mean of £193.3 and a standard deviation of £262.4, the simulation averages from Table 15. It is found that the sample mean and sample standard deviation with this distribution both lie below the conditioned observed values, £157.29, and £184.78, on 93 occasions out of 1,000. This implies that the true values for the mean and standard deviation might be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 9.3%. This single-sided probability is well above the double-sided probability of between 1% and 5% below which the credibility of a model is conventionally regarded as suspect.
is lognormal with a mean of £193.3 and a standard deviation of £262.4, the simulation averages from Table 15. It is found that the sample mean and sample standard deviation with this distribution both lie below the conditioned observed values, £157.29, and £184.78, on 93 occasions out of 1,000. This implies that the true values for the mean and standard deviation might be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 9.3%. This single-sided probability is well above the double-sided probability of between 1% and 5% below which the credibility of a model is conventionally regarded as suspect.
This suggests that there are no grounds for regarding the model incorporating the Extended Piecewise Uniform distribution for MAP ratio as inadequate for Phase 1. This provides validation for the finding that the average MAP ratio for discriminating Phase 1 respondents is close to 2.0.
C.3 Modeling the Output Distribution for V(F3) in Phase 2
The absence of Types 2 and 3 indiscrimination in Phase 2 means that it is possible to use the observed means and standard deviations listed in Table 4 for both  and
and  without the conditioning required in Phase 1. The modeling then follows the pattern laid out in Section C.2.
without the conditioning required in Phase 1. The modeling then follows the pattern laid out in Section C.2.
A single mean and variance for the MAP ratio,  , is found under the assumption of an Extended Piecewise Uniform distribution for MAP ratio using the methods of Appendix B. See Table 14. The action of the Extended Piecewise Uniform distribution for MAP ratio on the input distribution for
, is found under the assumption of an Extended Piecewise Uniform distribution for MAP ratio using the methods of Appendix B. See Table 14. The action of the Extended Piecewise Uniform distribution for MAP ratio on the input distribution for  is then modeled using Equations (E.3) and (E.9) from Appendix E to calculate analytically the parameters of the output distribution,
is then modeled using Equations (E.3) and (E.9) from Appendix E to calculate analytically the parameters of the output distribution, .
.
An exact match with the observed mean for , £145.1, is produced when
, £145.1, is produced when , suggesting that there may be a negative correlation between input valuation,
, suggesting that there may be a negative correlation between input valuation,  , and MAP ratio. However such a correlation is very weak:
, and MAP ratio. However such a correlation is very weak: . It is concluded that models assuming independence between
. It is concluded that models assuming independence between  and
and  are likely to be adequate.
are likely to be adequate.
Table 16 shows the predicted parameters for  from the analytic and the simulation methods under the assumption of independence between
from the analytic and the simulation methods under the assumption of independence between  and
and , and compares these with the observed parameters. The closeness of the match is illustrated by Figure 2, which compares the numbers in valuation intervals of £25 for (i) the observed distribution for discriminating and Type 1 respondents, (ii) one realization of 52 people chosen to have a sample mean and sample variance each close to the figures of Table 16 and (iii) for the calculated distribution based on simulation averages from Table 16.
, and compares these with the observed parameters. The closeness of the match is illustrated by Figure 2, which compares the numbers in valuation intervals of £25 for (i) the observed distribution for discriminating and Type 1 respondents, (ii) one realization of 52 people chosen to have a sample mean and sample variance each close to the figures of Table 16 and (iii) for the calculated distribution based on simulation averages from Table 16.
A further way of judging the proximity of the results to the observation is found by carrying out 1,000 simulations of cohorts of 52 people when it is assumed that the distribution for  is lognormal with a mean of £168 and a standard deviation of £236.3, the simulation averages given in Table 16. It is found that the sample mean with this distribution lies below the observed values of sample mean, £145.14, and sample standard deviation, £199.6, on 218 occasions out of 1,000. This implies that the true values for the mean and standard deviation could be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 21.8%, substantially above the level at which the credibility of a model is conventionally regarded as suspect.
is lognormal with a mean of £168 and a standard deviation of £236.3, the simulation averages given in Table 16. It is found that the sample mean with this distribution lies below the observed values of sample mean, £145.14, and sample standard deviation, £199.6, on 218 occasions out of 1,000. This implies that the true values for the mean and standard deviation could be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 21.8%, substantially above the level at which the credibility of a model is conventionally regarded as suspect.
Again no good grounds have been found for regarding the model incorporating the Extended Piecewise Uniform distribution for MAP ratio as inadequate for Phase 2. This provides validation for the finding that the average MAP ratio for discriminating respondents in Phase 2 is close to 2.0.
Appendix D. Additional Validation of the Results of the Truncated Lognormal Distribution Model
Simulation may be used to find the distribution for  from the distribution for
from the distribution for  when the Truncated Lognormal distribution is used to represent the MAP ratio.
when the Truncated Lognormal distribution is used to represent the MAP ratio.
D.1 Phase 1
Table 17 compares the distribution parameters found by simulating the decisions of 200 cohorts of 67 respondents using the Truncated Lognormal distribution to represent the behavior of the MAP ratio, . The parameters are very similar to those of produced using the Extended Piecewise Uniform distribution, and to those observed. See Figure 3.
. The parameters are very similar to those of produced using the Extended Piecewise Uniform distribution, and to those observed. See Figure 3.
Based on a thousand simulations of groups of 67, where 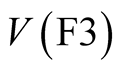 is assumed to follow a lognormal distribution with a mean of 194 and a standard deviation of 261.7, (see Table 17), both the sample mean and sample standard deviation will fall below the reported values of 157.3 and 184.8 in 95 cases in 1,000, implying that the true values for the mean and standard deviation could be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 9.5%, well above the level at or below which the credibility of a model is conventionally regarded as suspect.
is assumed to follow a lognormal distribution with a mean of 194 and a standard deviation of 261.7, (see Table 17), both the sample mean and sample standard deviation will fall below the reported values of 157.3 and 184.8 in 95 cases in 1,000, implying that the true values for the mean and standard deviation could be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 9.5%, well above the level at or below which the credibility of a model is conventionally regarded as suspect.
The good match suggests that the model incorporating the Truncated Lognormal distribution for MAP ratio provides a reasonable model for Phase 1, thus providing further validation for the finding that the average MAP ratio for discriminating respondents in Phase 1 is close to 2.0.
D.2 Phase 2
Table 18 compares the distribution parameters found by simulating the decisions of 200 groups of 52. The results are reasonably close, both to the results based on an Extended Piecewise Uniform distribution for MAP ratio and to the observed data. See Figure 4.
Based on a thousand simulations of groups of 52, where the valuation of [R3] is assumed to follow a lognormal distribution characterized by a mean of 176.7 and a standard deviation of 250.9 (see Table 18), the sample mean and sample standard deviation of the realized sample of 52 will each be less than the reported values of 145.14 and 199.60 in 156 cases in 1,000, implying that the true values for the mean and standard deviation could be those suggested by the model but the values recorded in an experiment could still be as low as or lower than those recorded in the Caveat Investigator study with a probability of about 15.6%, again well above the probability at which the credibility of a model is conventionally called into question.
Once again the model is found not to be inconsistent with the observations, providing validation for the Truncated Lognormal distribution for MAP ratio, and, in particular, the finding that the average MAP ratio for discriminating respondents in Phase 2 is close to 2.0.
Appendix E. Mean and Standard Deviation of the Product of Two Random Variables
In general, if  is a function of two random variables
is a function of two random variables  and
and  with means
with means  and
and  and variances
and variances  and
and , then a first-order Taylor series expansion about the point,
, then a first-order Taylor series expansion about the point,  gives:
gives:
 (E.1)
(E.1)
Hence
 (E.2)
(E.2)
where  is the covariance of
is the covariance of  and
and , or
, or
 (E.3)
(E.3)
where  is the correlation coefficient relating the covariance to the standard deviations:
is the correlation coefficient relating the covariance to the standard deviations:  .
.
A second order Taylor series may be invoked in order to determine the mean:
 (E.4)
(E.4)
Applying the expectation operator produces:
 (E.5)
(E.5)
or
 (E.6)
(E.6)
In the case of a product, where , then
, then  and
and
 (E.7)
(E.7)
Evaluating those derivatives at  and putting the results into Equation (E.3) gives:
and putting the results into Equation (E.3) gives:
 (E.8)
(E.8)
while applying the derivatives and the definition of  to Equation (E.6) gives:
to Equation (E.6) gives:
 (E.9)
(E.9)
The equality is exact as written in Equation (E.9), rather than merely approximately true when the function,  , denotes a product. This follows from expanding the definition of covariance:
, denotes a product. This follows from expanding the definition of covariance:
 (E.10)
(E.10)
from which Equation (E.9) follows.