DVL/RPM Based Velocity Filter Aiding in the Underwater Vehicle Integrated Inertial Navigation System ()
1. Introduction
The Inertial Navigation System (INS) is designed to provide on attitude, velocity and position of vehicle using the gyro and accelerometer, which measure the angular velocity and the specific force independent of effects from the environment. Though the INS is correct in short period of time, its information gets incorrect as the time passes by because of its characteristic of getting the information using the integration of angular velocity and acceleration as well as its accumulated errors in sensor and initial arrangement. Generally, the position error of navigation system which acquires motion information from INS is increased as operation time goes. To overcome this weakness of INS, there are a lot of methods such as using the external devices such as GPS (global positioning system), speedometer, barometer, and magnetic compass. Especially on land, the integrated navigation system using GPS is widely used [1] [2] .
Performing reliable localization and navigation within highly unstructured underwater environments is a difficult task. The ultrasonic locating systems such as LBL (Long Baseline) and USBL (Ultra Short Baseline) are widely used for the underwater vehicle as the electric wave does not penetrate the water. Even though LBL is widely used and has good capability, it is hard to install and expensive. The navigation area is also restricted by range of LBL sensor located on undersea floor. In addition, it has the long sampling period due to the features of ultrasonic sounds. In case of USBL, it is easy to use as it can be used in low power and low price. But as the measuring distance gets distant, even the best USBL cannot control the underwater navigation on its own [3] - [5] .
The integrated navigation sensor using DVL (Doppler Velocity Log) is also widely used to improve the underwater navigation performance [6] [7] . DVL is the sensor for measuring the velocity of the underwater vehicle. It is designed to prevent the positioning from divergence to get the improved navigation. But its range of measuring depends on the altitude of sea. So, once the altitude of sea gets too deep during the navigation, it suddenly cannot measure the velocity. So, the DVL has limitation as the INS-DVS navigation tool. Accordingly, the special algorithm is required to merge the INV and external sensor.
In this paper, the goal is to develop the algorithm for integrated navigation of INS and velocity in order to improve the navigation performance of underwater vehicle in the sea water where the GPS electric wave cannot reach. The underwater vehicle will have the INS, depth sensor, ES (Echo Sounder), and DVL. Here the only device used to measure the velocity as external sensor is DVL. However, as the DVL’s measuring scope depends on the characteristics of sensors, the general navigation using INS-DVL has its limit. For overcoming the limitation, the proposal is the velocity filter which uses the information from RPM (Revolve Per Minutes) of the underwater vehicle. The velocity filter is basically composed of the DVL, RPM, and ES and is realized using the Kalman filter. The integrated navigation filter is composed of the indirect feedback extended Kalman filter [8] . At this time, the difference between velocities obtained from velocity filter and pure navigation method is used as the measured value. To verify the performance of the proposed algorithm, simulation with scenario trajectory was conducted. The final results were compared with the PINS and conventional integrated navigation method for performance analysis.
2. Underwater Integrated Navigation Algorithm
In this paper, the algorithm for underwater vehicle using the external velocity information was proposed to overcome the accumulated errors of velocity and position when the INS is used for double integration. Figure 1 shows the structure of algorithm for integrated navigation of the underwater vehicle.
SDINS (Strapdown Inertial Navigation System) was conducted using the angular velocity and specific force in the navigation coordinate system which was measured by IMU (Inertial Measurement Unit) composed of gyro and accelerometer. The positioning from SDINS showed the divergence due to the error of sensor and double integration. For estimation of the navigation error, the extended Kalman filter was designed to get the final navigational positioning using the indirect feedback method. At this time, the errors and compensate the variable of state were updated using the difference between velocity from SDINS and velocity form external sensor as the value from extended Kalman filter. Generally to get the velocity of the underwater vehicle, DVL and EM- log are widely used. DVL was used for external velocity information for underwater vehicle and the study on the integrated navigation of INS-DVL was actively performed. However, the DVL’s range of measuring varied depending on the characteristics of sensor. So, if the sea gets too deep suddenly, it cannot measure the velocity. To complement such a weak point, the velocity filter was additionally designed, which is made of DVL, RPM, and ES. The basic concept is to use the RPM as the velocity information. For detail on the velocity filter, see Section 2.2 Design of Velocity Filter.
![]()
Figure 1. Structure of underwater integrate navigation system.
2.1. Integrated Underwater Navigation System Using the Indirect Feedback Kalman Filter
INS system has the non-radiating and non-jamming features that it is not affected by the external environment. So, due to this big advantage, it is used as the main navigation system. The differential equation for velocity in the NED (north east down) frame of SDINS can be summed as follows
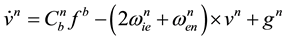 (1)
(1)
where
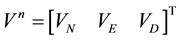 , (2)
, (2)
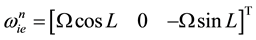 , (3)
, (3)
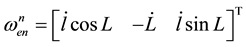 , (4)
, (4)
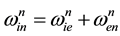 . (5)
. (5)
Here 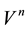 means the velocity in the NED frame while
means the velocity in the NED frame while 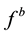 and
and 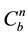 are specific force in body frame and the DCM (Direction Cosine Matrix) respectively. Ω indicates the angular velocity of Earth’s rotation and L means the latitude while l indicates longitude and
are specific force in body frame and the DCM (Direction Cosine Matrix) respectively. Ω indicates the angular velocity of Earth’s rotation and L means the latitude while l indicates longitude and 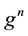 means the gravitation depending on the latitude [1] .
means the gravitation depending on the latitude [1] .
The differential equation for DCM is as follows
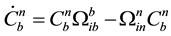 (6)
(6)
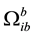 is the measured value of gyro
is the measured value of gyro 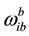 and
and 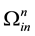 is composed of the rates of changes in angular velocity of Earth’s rotation, latitude and longitude. It is the skew-symmetric matrix. To induce the error model for Equation (1) of velocity differential equation and Equation (6) for attitude differential equation, the perturbation method was used. The perturbation method is to interpret the system by using the difference between variables obtained from navigation algorithm and actual values as the error variables. If it is assumed that there is error in position, velocity, attitude and sensor, the perturbation method to induce the navigation error model can be used.
is composed of the rates of changes in angular velocity of Earth’s rotation, latitude and longitude. It is the skew-symmetric matrix. To induce the error model for Equation (1) of velocity differential equation and Equation (6) for attitude differential equation, the perturbation method was used. The perturbation method is to interpret the system by using the difference between variables obtained from navigation algorithm and actual values as the error variables. If it is assumed that there is error in position, velocity, attitude and sensor, the perturbation method to induce the navigation error model can be used.
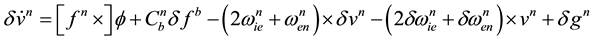 (7)
(7)
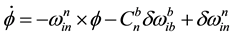 (8)
(8)
At this time, the velocity information is the only one as the external sensor. So the parts which are concerned with the position error is except from the navigation error model because if updated they tend to divergence.
So, it can be rearranged as follows.
![]() (9)
(9)
![]() (10)
(10)
After the combination of the velocity error with the differential equation of position error obtained from Equations (9) and (10), the time varying linear system can be obtained as follows.
![]() (11)
(11)
![]() (12)
(12)
Here ![]() is the 12th variable of state composed of velocity error
is the 12th variable of state composed of velocity error![]() , attitude error
, attitude error![]() , accelerometer bias
, accelerometer bias ![]() and gyro bias
and gyro bias ![]() of the underwater vehicle.
of the underwater vehicle.
![]()
![]() is the assumed noise of system and it is the White Gaussian noise with the average of 0 and the variance of Q. The time varying system matrix
is the assumed noise of system and it is the White Gaussian noise with the average of 0 and the variance of Q. The time varying system matrix ![]() is as follows.
is as follows.
![]() (13)
(13)
![]() (14)
(14)
![]() (15)
(15)
Once the equation for measuring error from SDINS and velocity filter are obtained, the measuring model equation for Kalman filter is as follows.
![]() (16)
(16)
![]() (17)
(17)
![]() (18)
(18)
In the equations above, ![]() is the assumed system noise and it is the White Gaussian noise with the average of 0 and the variance of Q. At this time, Q of the integrated navigation filter is selected taking into consideration the characteristic of IMU noise. R has been properly adjusted before adopted.
is the assumed system noise and it is the White Gaussian noise with the average of 0 and the variance of Q. At this time, Q of the integrated navigation filter is selected taking into consideration the characteristic of IMU noise. R has been properly adjusted before adopted.
2.2. Design of Velocity Filter
The basic concept of velocity filter is the velocity information other than DVL. It used the RPM. The equation which converts the RPM into the velocity is as follows.
![]() (20)
(20)
Here, ![]() is the estimated velocity, and rpm is the current motor’s RPM while
is the estimated velocity, and rpm is the current motor’s RPM while ![]() is scale factor which uses the DVL to convert the RPM into the velocity and b is the bias of RPM. DVL is used on real time basis to assume the conversion scale factor and bias for the RPM. If the use of DVL is impossible, the finally assumed value will be used in a way RPM is converted to the velocity. At this time, whether the DVL is used is determined by the ES. Figure 2 shows the detailed structure of velocity filter.
is scale factor which uses the DVL to convert the RPM into the velocity and b is the bias of RPM. DVL is used on real time basis to assume the conversion scale factor and bias for the RPM. If the use of DVL is impossible, the finally assumed value will be used in a way RPM is converted to the velocity. At this time, whether the DVL is used is determined by the ES. Figure 2 shows the detailed structure of velocity filter. ![]() and
and ![]()
![]() are the velocities of DVL and the converted RPM against x, y and z axes in the NED frame while
are the velocities of DVL and the converted RPM against x, y and z axes in the NED frame while ![]() indicate the forward velocity against the body frame. The rev means the RPM of motor of the underwater vehicle while the altitude shows the water depth measured by ES. Scale factor and bias are the assumed values of scale factor for RPM and bias. It is assumed that DVL can measure the roll (Φ), pitch (θ) and yaw (Ψ) and that using the azimuth meter and inclinometer it can convert the velocity measured by the underwater vehicle to the velocity for NED frame. The measured value of velocity filter is the component of DVL. To assume the conversion factory of RPM and bias, the same coordinate system should be used. In this paper, the filter was designed based on the body frame. That is because the RPM can be deemed as the velocity component of the forward direction of body frame. It means that the velocity filter is made with the DVL, and RPM information. The equation to convert the DVL in three axes in the NED frame to the forward velocity of body frame is as follows.
indicate the forward velocity against the body frame. The rev means the RPM of motor of the underwater vehicle while the altitude shows the water depth measured by ES. Scale factor and bias are the assumed values of scale factor for RPM and bias. It is assumed that DVL can measure the roll (Φ), pitch (θ) and yaw (Ψ) and that using the azimuth meter and inclinometer it can convert the velocity measured by the underwater vehicle to the velocity for NED frame. The measured value of velocity filter is the component of DVL. To assume the conversion factory of RPM and bias, the same coordinate system should be used. In this paper, the filter was designed based on the body frame. That is because the RPM can be deemed as the velocity component of the forward direction of body frame. It means that the velocity filter is made with the DVL, and RPM information. The equation to convert the DVL in three axes in the NED frame to the forward velocity of body frame is as follows.
![]() (21)
(21)
The input value of velocity filter is v of DVL of vehicle body frame and RPM (rev). The system equation and measuring equation for this are as follows.
![]() (22)
(22)
![]() (23)
(23)
![]()
Figure 2. Structure of velocity Kalman filter.
where,
![]() , (24)
, (24)
Measurement equation is as follows:
![]() (25)
(25)
![]() (26)
(26)
If the scale factor and bias through Kalman filter are used and the Equation (20) is applied, it is assumed that the velocity on the RPM on the body frame. In addition, if the velocity on RPM in the body frame is converted, the velocity on the three axes on the NED frame is obtained. Equation (27) shows the equation for conversion of coordinate system.
![]() (27)
(27)
where
![]() (28)
(28)
Finally, the velocity and altitude data for the three axes of NED frame of the DVL and RPM enter into the final switching box. Depending on the altitude, it judges which data it uses. This is indicated in Equation (29).
![]() (29)
(29)
3. Simulation
3.1. Description of Simulation
The simulation was conducted to verify the performance of integrated navigation system to which the velocity filter is applied. First the trajectory is created assuming the position and attitude using the initial velocity, cruise velocity, and running time only. Then, based on the created trajectory, the INS is made in the reverse form in order to model IMU. Then, the differentiation of position on the created trajectory leads to the velocity and the differentiating of velocity and removing the gravitational acceleration lead us to get the signal of accelerometer. At this time, the Coriolis compensation was used. The signal of angular velocity of gyro was created by differentiating the attitude. The gravitational acceleration, Earth’s gravitational acceleration and radius of the Earth were updated for every sample. Based on the created IMU signal, the PINS was conducted to get the position, velocity and attitude. At this time, by including the coning and sculling and other precision error factor, the navigational solution is obtained. At the same time, the external sensor is modeled for the integrated navigation system. Using the velocity information obtained by differentiating the position solution obtained from the created trajectory, DVL and RPM signals are modeled. The ES is modeled too considering the time of total simulation. Using this external sensor signals, the velocity filter is conducted which is the core of this paper. At this time, the value of velocity can be used as the error value for the integrated navigational filter to get the final error of navigational solution. Figure 3 shows the total sequence of the simulation.
3.2. Simulation Environment
The simulation result was derived by using the MATLAB of MathWorks. The trajectory and the integrated navigational algorithm were created by using m-code. All calculations for simulation were conducted with 100 Hz while DVL signal was modeled using 5 Hz for calculation. IMU was modeled assuming that it belongs to 1 deg/hr. It was created assuming that the error characteristics of Honeywell’s HG I700 (1 deg/hr) has the correct and verified specification. Table 1 shows the IMU’s error characteristics.
In this paper, the external sensor was modeled in a simple way. DVL was modeled by adding the error factor to the velocity obtained by differentiating the created trajectory. It was assumed that DVL’s velocity information has the error of 0.2% and was modeled to have the error of ±0.2% for every simulation. The bias error was designed to include ±0.5 m/s when the simulation is conducted before the noise error was added. The modeling of DVL is as shown in Equations (30)-(32).
![]() (30)
(30)
![]() (31)
(31)
![]()
Table 1. IMU modeling specification.
![]() (32)
(32)
In the equation above, sf is the error in scale factor, and b is the bias, while ![]() is the white noise. It was assumed that the DVL can be operated at the altitude of 100 m based on the underwater vehicle. In case of exceeding 100 m, the noise of ±5 m/s was added to the DVL velocity information. RPM was modeled using the velocity information obtained from created trajectory. In case of ES, the modeling was made in a way that the DVL is get out of the 2 zones considering the DVL operational range. The total time of simulation is 24 minutes and the velocity of underwater vehicle was estimated to be 10 knot.
is the white noise. It was assumed that the DVL can be operated at the altitude of 100 m based on the underwater vehicle. In case of exceeding 100 m, the noise of ±5 m/s was added to the DVL velocity information. RPM was modeled using the velocity information obtained from created trajectory. In case of ES, the modeling was made in a way that the DVL is get out of the 2 zones considering the DVL operational range. The total time of simulation is 24 minutes and the velocity of underwater vehicle was estimated to be 10 knot.
3.3. Simulation Result
Figure 4 shows the created 3D navigational trajectory. Figure 5 shows the output of accelerometer and gyro when position and attitude values are differentiated based on the trajectory and the sensor error is added.
Based on the angular velocity, the attitude was derived. This is shown in Figure 5. Based on the created angular velocity, and acceleration, the PINS was performed and Figure 10 shows the final comparative results. As expected, the result of PINS shows the divergence according to the accumulated errors. To make up for this error, we designed the velocity filter. The input values such as the DVL’s velocity, RPM, and altitude of ES are as shown in Figure 6 and Figure 7. If we look at Figure 6, we can understand that DVL gets out of its operation range for 4 minutes such as zone of 5 - 8 minutes and zone of 15 - 16 minutes. We assumed that the operational range of the vehicle is 100 m as we specified in 3.2. If we look at the data of ES, it is understood that the zone exceeding the altitude of 100 m has been modeled. If we apply the velocity Kalman filter using modeled external sensor is used, the scale factor for the RPM’s velocity change, which are the assumed value, and bias are shown in Figure 8.
The first graph in Figure 8 shows the velocity of DVL which represents the forward velocity of body frame at the NED frame while the scale factor assumed on real time and the bias are shown in second and third graphs. In case of the process in which the scale factor is assumed, the scale factor and bias are estimated on real time in the zone where the DVL can be operated. But, once it is out of the zone, we can see that the final assumed value is used. The finally assumed scale factor and bias convert the RPM into the velocity. Then, the result of comparison with the DVL velocity at the NED frame is shown in Figure 9. The line shows the velocity measured by DVL while the dotted line shows the velocity information using RPM. As expected, if the DVL is over the operational zone, the noise is added so that the velocity value cannot be relied upon. At this time, the velocity using RPM is well assumed. When the coordinate is converted, the Euler angle is used and the divergence appears. But it shows the result that it can be used as the velocity information of integrated navigation filter.
The final integrated navigations result is shown in Figure 10. The picture left shows the comparison between
![]()
Figure 9. Velocity result estimated by RPM.
correct answer and the PINS trajectory. The picture in the middle shows the comparison with the conventional INS-DVL integrated navigational method while the picture on the right shows the comparison with INS-DVL integrated navigation method where the velocity filter is applied. When the error based on the starting point and ending point, is calculated, the pure navigational method showed the error of 21,181 m, general INS-DVL method showed 1117 m while the INV-DVL applied with the velocity filter showed the error of 209 m, showing that the result of integrated INS-DVL navigational method has the significant reduced error than other methods. Actually when the DVL is used, there are cased when the error gets bigger if the sensor gets out of its range of capacity but it has advantages because it does not get un-dispersed result if the velocity is compensated.
4. Conclusions
In this paper, the integrated algorithm was developed using the INS and velocity information to improve the navigational capability of underwater vehicle having a long range of maneuverability in the sea where the GPS electric wave did not reach. It was proposed that the velocity did use not only the general external sensor but also the RPM of the underwater vehicle, thus improving the navigation performance. The suggested algorithm was verified by the simulation which showed that it was better than the PINS or conventional integrated navigational method.
In the further research, it is required to enhance the precision of DVL and RPM model. In the case of RPM model, the characteristics of motor and propeller could be considered to mimic real RPM behavior. The time delay factor should be also considered to make more precise DVL model when the depth of navigation body is out of DVL’s measurement range. Close eye shall be focused on the error caused by the current in the sea considering the non-linearity of the underwater environment. Finally it is required to need to conduct the repetitive simulation in actual environment for final verification of the proposed algorithm.