On the Connection between the Hamilton-Jacobi-Bellman and the Fokker-Planck Control Frameworks ()
1. Introduction
In the modelling of uncertainty, the theory of stochastic processes [1] provides established mathematical tools for the modelling and the analysis of systems with random dynamics. Furthermore in application, the possibility to control sequences of events subject to random disturbances is highly desirable for real applications. In this paper, we elucidate the connection between the well established Hamilton-Jacobi-Bellman (HJB) control frame- work [2] [3] and a control strategy based on the Fokker-Planck (FP) equation [4] [5] . Illustrative examples allow gaining additional insight on this connection.
We focus on a representative n-dimensional continuous-time stochastic processes described by the following model
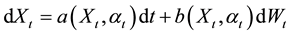 (1.1)
(1.1)
where 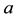 is a Lipschitz-continuous n-dimensional drift function and
is a Lipschitz-continuous n-dimensional drift function and 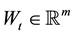 is a m-dimensional Wiener process with stochastically independent components. The dispersion function
is a m-dimensional Wiener process with stochastically independent components. The dispersion function 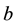 with values in
with values in 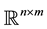 is assumed to be smooth and full rank; see [6] . This is the well-known Itō stochastic differential equation (SDE) [1] where we consider also the action of a d-components vector of controls
is assumed to be smooth and full rank; see [6] . This is the well-known Itō stochastic differential equation (SDE) [1] where we consider also the action of a d-components vector of controls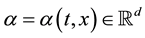 , that allows driving the random process towards a certain goal [3] . We denote with
, that allows driving the random process towards a certain goal [3] . We denote with 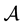 the set of Markovian controls that contains
the set of Markovian controls that contains
all jointly measurable functions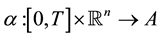 , where
, where 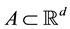 is a given compact set [3] . In determinis-
is a given compact set [3] . In determinis-
tic dynamics, the optimal control is achieved by finding a control law 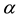 that minimizes a given objective defined by a cost functional
that minimizes a given objective defined by a cost functional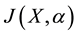 ; see, e.g., [2] .
; see, e.g., [2] .
In the non-deterministic case, the state 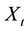 is random, so that inserting a stochastic process into a deterministic cost functional will result into a random variable. Therefore, in stochastic optimal control prob- lems the expected value of a given cost functional is considered [7] . In particular, we have
is random, so that inserting a stochastic process into a deterministic cost functional will result into a random variable. Therefore, in stochastic optimal control prob- lems the expected value of a given cost functional is considered [7] . In particular, we have
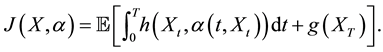 (1.2)
(1.2)
This is a Bolza type cost functional in the finite-horizon case 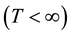 and it is assumed here that the controller knows the state of the system at each instant of time (complete observations). For this case, the method of dynamic programming can be applied [2] [7] [8] in order to derive the HJB equation for
and it is assumed here that the controller knows the state of the system at each instant of time (complete observations). For this case, the method of dynamic programming can be applied [2] [7] [8] in order to derive the HJB equation for 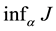 with
with 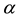 as the optimization function. Some other cases of the cost structure of
as the optimization function. Some other cases of the cost structure of ![]() are quoted in [8] , that have applications in finance, engineering, and in production planning and forest harvesting. Each
are quoted in [8] , that have applications in finance, engineering, and in production planning and forest harvesting. Each ![]() will lead to a different form of the HJB equation that can be analysed with appropriate methods of partial differential equa- tions; see, e.g., [9] .
will lead to a different form of the HJB equation that can be analysed with appropriate methods of partial differential equa- tions; see, e.g., [9] .
A control approach close to the HJB formulation consists in approximating the continuous stochastic process by a discrete Markov decision chain. In this approach the information of the controlled stochastic process, carried by the transition probability density function of the approximating Markov process, is utilized to solve the Bellman equation; for details see [10] .
However, the common methodology to find an optimal controller of random processes consists in reformulat- ing the problem from stochastic to deterministic. This is a reasonable approach when we consider the problem from a statistical point of view, with the purpose to find out the collective “ensemble” behaviour of the process. In fact, the average ![]() of the functional of the process
of the functional of the process ![]() is omnipresent in almost all stochastic optimal control problems considered in the scientific literature.
is omnipresent in almost all stochastic optimal control problems considered in the scientific literature.
The value of the cost functional before averaging is a way to measure the cost of a single trajectory of the process. However, the knowledge of the single realization is not useful for the statistical analysis, that would require to determine the average, the variance, and other properties associated to the state of the stochastic process.
On the other hand, a stochastic process is completely characterized by its law which, in many cases, can be represented by the probability density function (PDF). Therefore, a control methodology that employs the PDF would provide an accurate and flexible control strategy that could accommodate a wide class of objectives. For this reason, in [11] - [14] PDF control schemes were proposed, where the cost functional depends, possibly non- linearly, on the PDF of the stochastic state variable; see, e.g., [11] - [14] for specific applications.
The important step in the Fokker-Planck control framework proposed in [4] [5] is to recognize that the evolution of the PDF associated to the stochastic process (1.1) is characterized as the solution of the Fokker- Planck (also known as forward Kolmogorov) equation; see, e.g., [15] [16] . This is a partial differential equation of parabolic type with Cauchy data given by the initial PDF distribution. Therefore, the formulation of objec- tives in terms of the PDF and the use of the Fokker-Planck equation provide a consistent framework to formu- late an optimal control strategy of stochastic processes.
In this paper, we discuss the relationship between the HJB and the FP frameworks. We show that the FP control strategy provides the same optimal control as the HJB method for an appropriate choice of the objectives. Specifically, this is the case for objectives that are formulated as expected cost functionals and assuming that both the HJB equation and the FP equation admit a unique classical solution. The latter assumption is motivated by the purpose of this work to show the connection between the HJB and FP frameworks, without aiming at finding the most general setting, e.g. for viscosity solution of the HJB equation [9] [17] [18] or FP equation with irregular coefficients [19] , where this connection holds. Furthermore, we remark that the FP approach allows accommodating any desired functional of the stochastic state and its density, that is now represented by the PDF associated to the controlled stochastic process.
In the next section, we illustrate the HJB framework. In Section 3, we discuss the FP method. Section 4 is devoted to specific illustrative examples. A section of conclusions completes this paper.
2. The HJB framework
We consider the optimal control of the state ![]() whose evolution is governed by drift and random diffusion as follows
whose evolution is governed by drift and random diffusion as follows
![]() (1.3)
(1.3)
The control function ![]() use the current value
use the current value ![]() to affect the dynamics of the stochastic process by adjusting the drift and the dispersion function.
to affect the dynamics of the stochastic process by adjusting the drift and the dispersion function.
We define the expected cost for the admissible controls ![]() as follows
as follows
![]() (1.4)
(1.4)
which is an expectation conditional to the process ![]() taking the value
taking the value ![]() at time
at time![]() . Here,
. Here, ![]() solves the stochastic differential equation (1.3) with control
solves the stochastic differential equation (1.3) with control ![]() and the following functions
and the following functions
![]()
are smooth and bounded. We call ![]() the running cost and
the running cost and ![]() the terminal cost. Our goal is to find an optimal
the terminal cost. Our goal is to find an optimal
control ![]() which minimizes the expected cost
which minimizes the expected cost ![]() for the process (1.3), namely
for the process (1.3), namely
![]() (1.5)
(1.5)
We assume that this control is unique. Further, we define the following value function, also known as the cost to go function,
![]() (1.6)
(1.6)
It is well known [2] [3] that ![]() solves the Hamilton-Jacobi-Bellman equation and that the optimal control can be reconstructed from
solves the Hamilton-Jacobi-Bellman equation and that the optimal control can be reconstructed from![]() . Assume that the optimal control is unique and is attained, then we have
. Assume that the optimal control is unique and is attained, then we have
![]()
In the following, to ease notation we use the Einstein summation convention: when an index variable appears twice in a single term this means that a summation over all possible values of the index takes place. For exam-
ple, we have that![]() . Moreover,
. Moreover, ![]() ,
, ![]() denotes derivative with respect to the
denotes derivative with respect to the
variable![]() , and
, and ![]() denotes partial derivative with respect to the time variable.
denotes partial derivative with respect to the time variable.
Theorem 1. Assume that ![]() solves (1.3) with a Markov control function
solves (1.3) with a Markov control function ![]() and that the function
and that the function ![]() defined by (1.6) is bounded and smooth. Then
defined by (1.6) is bounded and smooth. Then ![]() satisfies the following Hamilton-Jacobi-Bellman equation
satisfies the following Hamilton-Jacobi-Bellman equation
![]() (1.7)
(1.7)
with the Hamiltonian function
![]() (1.8)
(1.8)
and![]() .
.
Notice that the optimal control satisfies at each time ![]() and state
and state ![]() the following optimality condition
the following optimality condition
![]() (1.9)
(1.9)
Existence and uniqueness of solutions to the HJB equation often involve the concept of uniform parabolicity; see [3] [18] [20] . The HJB equation is called uniformly parabolic [3] if there exists a constant ![]() such that, for all
such that, for all ![]() and
and![]() , the following holds
, the following holds
![]()
where ![]() represents a bounded or unbounded set.
represents a bounded or unbounded set.
If the non-degeneracy condition holds, results from the theory of PDEs of parabolic type imply existence and uniqueness of solutions to the HJB problem (1.7) with the properties required in the Verification Theorem [3] . In particular, we have the following theorem due to Krylov.
Theorem 2. If the non-degeneracy assumption holds, and in addition we have that ![]() is compact,
is compact, ![]() is bounded with
is bounded with![]() , the drift, the diffusion, and the Lagrange functions are sufficiently smooth on the space-time cylinder
, the drift, the diffusion, and the Lagrange functions are sufficiently smooth on the space-time cylinder![]() , and the final condition is
, and the final condition is![]() , then the HJB has a unique solution
, then the HJB has a unique solution
![]() .
.
3. The Fokker-Planck formulation
In this section, we discuss an alternative to the HJB approach that is based on the formulation of a Fokker- Planck optimal control problem. We suppose that the functions ![]() and
and ![]() of (1.3) yield a stochastic process
of (1.3) yield a stochastic process ![]() for which it exists an absolutely continuous measure. Thus,
for which it exists an absolutely continuous measure. Thus, ![]() denotes the PDF of the state variable
denotes the PDF of the state variable![]() , where the process starts at
, where the process starts at ![]() with initial value distributed according to the density
with initial value distributed according to the density![]() .
.
The time evolution of the PDF ![]() is governed by the Fokker-Planck equation
is governed by the Fokker-Planck equation
![]() (1.10)
(1.10)
Also in this case, the FP problem can be defined in a bounded or unbounded set in![]() . Existence and uniqueness to this problem often relay on the concept of uniform parabolicity as in Theorem 2. For the case
. Existence and uniqueness to this problem often relay on the concept of uniform parabolicity as in Theorem 2. For the case![]() , we refer to [19] [20] ; see also [21] and the references therein. Furthermore, we remark that in the case of bounded domains, boundary conditions for the FP model must be chosen that ought to be meaningful for the underlying stochastic process. This is a delicate issue that is not the focus of this work and therefore, in the following, we consider the common case where
, we refer to [19] [20] ; see also [21] and the references therein. Furthermore, we remark that in the case of bounded domains, boundary conditions for the FP model must be chosen that ought to be meaningful for the underlying stochastic process. This is a delicate issue that is not the focus of this work and therefore, in the following, we consider the common case where![]() .
.
Now, we consider a cost functional ![]() that is linear in
that is linear in![]() . In correspondence to this cost functional, we define the following PDE optimal control problem
. In correspondence to this cost functional, we define the following PDE optimal control problem
![]() (1.11)
(1.11)
It is important to recognize that if![]() , then we can write the cost functional
, then we can write the cost functional ![]() introduced in (1.4) as follows
introduced in (1.4) as follows
![]() (1.12)
(1.12)
that gives (1.4) in terms of the probability measure,![]() .
.
To characterize the optimal solution to (1.11) where the cost functional (1.4) is considered, we introduce the Lagrange functional [22] .
![]() (1.13)
(1.13)
where the function ![]() represents the Lagrange multiplier.
represents the Lagrange multiplier.
We have that the optimal control solution is characterized as the solution to the following optimality system
![]() (1.14)
(1.14)
![]() (1.15)
(1.15)
![]() (1.16)
(1.16)
where ![]() and
and![]() .
.
Now, we illustrate the equivalence between the HJB and the FP formulation. The key point is to notice that (1.16) corresponds to the first-order necessary optimality condition (1.9) for the minimization of the Hamil- tonian in the HJB formulation, once we identify the Lagrange multiplier ![]() with the value function
with the value function ![]() in (1.7). Therefore, provided that the minimization problem (1.11) admits a unique solution
in (1.7). Therefore, provided that the minimization problem (1.11) admits a unique solution ![]() in terms of the first- and second-order derivatives of
in terms of the first- and second-order derivatives of![]() , then we can replace such
, then we can replace such ![]() into the backward Kolmogorov equation (1.15), thus obtaining the HJB equation (1.7). This procedure results in the equation (1.15), because of the formal equivalence between (1.16) and (1.9). With our setting, since the solution
into the backward Kolmogorov equation (1.15), thus obtaining the HJB equation (1.7). This procedure results in the equation (1.15), because of the formal equivalence between (1.16) and (1.9). With our setting, since the solution ![]() of (1.7) is unique, then the uni- queness of
of (1.7) is unique, then the uni- queness of ![]() and
and ![]() follows; see [3] .
follows; see [3] .
Notice that with the above setting, the optimal control ![]() does not depend explicitly on the density
does not depend explicitly on the density![]() , but only on the Lagrange multiplier
, but only on the Lagrange multiplier![]() , that is the value function
, that is the value function![]() . (This explains why the feedback control is based on the value function.) Hence, the equations (1.15)-(1.16) determine the optimal control. This will not be the case in the more general situation in which the cost functional in (1.12) is not linear in
. (This explains why the feedback control is based on the value function.) Hence, the equations (1.15)-(1.16) determine the optimal control. This will not be the case in the more general situation in which the cost functional in (1.12) is not linear in![]() . This happens for instance when
. This happens for instance when ![]() does not represent an expected cost; see [4] [5] for the case of a tracking functional for the density.
does not represent an expected cost; see [4] [5] for the case of a tracking functional for the density.
We also note that the solution to the adjoint FP equation (1.15) and to the optimality condition equation for the control function (1.16) do not depend on the initial condition ![]() of the forward FP equation (1.14). Hence, according the HJB formulation, the solution to the backward Kolmogorov equation is not affected by the initial state of the system.
of the forward FP equation (1.14). Hence, according the HJB formulation, the solution to the backward Kolmogorov equation is not affected by the initial state of the system.
4. Illustrative examples
In this section, we consider two examples that illustrate that the FP optimal control formulation may provide the same control strategy as the HJB method. In the following, the first example refers to a Itōstochastic process, while the second example considers a piecewise deterministic process.
4.1. Controlled Itō stochastic process
We consider an optimal transport problem that is related to a model for mean-field games; see, e.g., [23] . It reflects the congestion situation, where the behaviour of the crowd depends on the form of the attractive strongly convex potential![]() . In this model, the dynamics of an agent is governed by the following stochastic differential equation
. In this model, the dynamics of an agent is governed by the following stochastic differential equation
![]()
where the velocity ![]() represents the controlling drift function and the dynamics is perturbed by random diffusion of intensity
represents the controlling drift function and the dynamics is perturbed by random diffusion of intensity![]() . With this setting, the evolution of the PDF for this process is given by the following FP equation
. With this setting, the evolution of the PDF for this process is given by the following FP equation
![]() (1.17)
(1.17)
where the PDF ![]() formally corresponds to the mass density of the transport problem.
formally corresponds to the mass density of the transport problem.
The purpose of the optimal control is to determine a drift of minimal kinetic energy that moves a mass distribution from an initial location to a final destination. The corresponding objective is as follows [24]
![]() (1.18)
(1.18)
In this functional, the kinetic energy term is augmented with the term ![]() that describes the
that describes the
attractive potential of the final destination. It can be interpreted as the requirement that the crowd aims at reaching the region of low potential ![]() at the terminal time
at the terminal time![]() .
.
The corresponding adjoint equation is given by the following backward evolution equation
![]() (1.19)
(1.19)
and the optimality condition is given by
![]() (1.20)
(1.20)
It is immediate to see that combining the adjoint equation and the optimality condition, we obtain the following HJB problem
![]() (1.21)
(1.21)
4.2. Controlled piecewise deterministic process
Our second example refers to a class of piecewise deterministic processes (PDP). A first general formulation of these systems that switch randomly within a certain number of deterministic discrete states at random times is given in [25] . Specifically, we deal with a PDP model described by a state function that is continuous in time and is driven by a discrete S-state renewal Markov process denoted with![]() ; see [26] for additional details. A switching control problem for ordinary differential equations has been investigated in [27] . In our case, the PDP equation model is a first-order differential equation, where the driving term is affected by the renewal process
; see [26] for additional details. A switching control problem for ordinary differential equations has been investigated in [27] . In our case, the PDP equation model is a first-order differential equation, where the driving term is affected by the renewal process
[28] . The state function![]() ,
, ![]() , is defined by the following properties [25] :
, is defined by the following properties [25] :
a) The state function satisfies the following equation
![]() (1.22)
(1.22)
where ![]() is a continuous-time Markov chain (defined below by c) and d)) with
is a continuous-time Markov chain (defined below by c) and d)) with ![]() discrete
discrete
states![]() . Correspondingly, given
. Correspondingly, given![]() , we say that the dynamics is in the (deterministic) state
, we say that the dynamics is in the (deterministic) state![]() ,
,
driven by the dynamics function![]() , that is taken from the set of functions
, that is taken from the set of functions![]() . We require
. We require
that all![]() ,
, ![]() , be Lipschitz continuous in
, be Lipschitz continuous in![]() , continuous in
, continuous in ![]() and bounded. With
and bounded. With
this assumptions for fixed![]() , the solution
, the solution ![]() exists and is unique and bounded. Furthermore, assuming that the sets of admissible controls
exists and is unique and bounded. Furthermore, assuming that the sets of admissible controls ![]() are closed and compact and a fixed initial condition is considered, then the
are closed and compact and a fixed initial condition is considered, then the
reachable set of trajectories is a closed bounded subset of![]() ; see [29] .
; see [29] .
b) The state function satisfies the initial condition ![]() being in the initial state
being in the initial state![]() .
.
c) The process ![]() is characterized by the pair
is characterized by the pair![]() , where the vector
, where the vector ![]() defines an exponential probability density function
defines an exponential probability density function![]() , of transition events, as follows
, of transition events, as follows
![]() (1.23)
(1.23)
for each state![]() ; and the stochastic transition probability matrix
; and the stochastic transition probability matrix ![]() governs the actual transition. The elements
governs the actual transition. The elements ![]() of the transition matrix satisfy the following properties
of the transition matrix satisfy the following properties
![]() (1.24)
(1.24)
When a transition event occurs, the PDP system switches instantaneously from a state![]() , with dynamic function
, with dynamic function![]() , randomly to a new state
, randomly to a new state![]() , driven by the dynamics function
, driven by the dynamics function![]() . Virtual transitions from the state
. Virtual transitions from the state ![]() to itself are allowed for this model, that is
to itself are allowed for this model, that is![]() .
.
We have that the time evolution of the PDFs of the states of our PDP model is governed by the following Fokker-Planck system [26]
![]() (1.25)
(1.25)
where ![]() if
if![]() , and
, and![]() ,
, ![]() , for the scalar process
, for the scalar process ![]() in the state
in the state![]() . We
. We
have![]() . We consider our PDP process in a finite-time horizon
. We consider our PDP process in a finite-time horizon![]() , and we have that
, and we have that
![]() (1.26)
(1.26)
The initial conditions for the solution of the FP system are given as follows
![]() (1.27)
(1.27)
Next, we consider an objective similar to (1.18) for all states of the system. We have
![]() (1.28)
(1.28)
This objective corresponds to the expected functional (1.4) on the space![]() .
.
Now, consider the FP optimal control problem of finding![]() ,
, ![]() , such that the objective (1.28) is minimized subject to the constraint given by (1.25). The solution to this problem is characterized by the solution of the corresponding FP optimality system, obtained by the Lagrange principle, consisting of (1.25) and the following
, such that the objective (1.28) is minimized subject to the constraint given by (1.25). The solution to this problem is characterized by the solution of the corresponding FP optimality system, obtained by the Lagrange principle, consisting of (1.25) and the following
![]() (1.29)
(1.29)
![]() (1.30)
(1.30)
![]() (1.31)
(1.31)
where (1.29)-(1.30) is the adjoint problem and (1.31) represents the optimality condition.
On the other hand, the HJB optimal control of our PDP model is considered in [29] , where the ![]() in [29] corresponds to our
in [29] corresponds to our![]() . In that reference, the following Hamiltonian for the state
. In that reference, the following Hamiltonian for the state ![]() is derived
is derived
![]() (1.32)
(1.32)
Furthermore, in [29] it is proved that the corresponding HJB problem
![]() (1.33)
(1.33)
admits a unique viscosity solution that is also the classical solution to the adjoint FP equation (1.29). Hence, also in this case the HJB formulation with (1.32) and (1.33) corresponds to the FP approach with (1.29) and (1.31), as much as the cost functions![]() , defined via the minimum of expected functionals correspond to the adjoint functions
, defined via the minimum of expected functionals correspond to the adjoint functions![]() .
.
5. Conclusion
In this paper, the connection between the Hamilton-Jacobi-Bellman dynamic programming scheme and a recently proposed Fokker-Planck control framework was discussed. It was shown that the two control strategies were equivalent in the case of mean cost functionals. To illustrate the connection between the two control strategies, the cases of an Itō stochastic process and of a piecewise-deterministic process were considered.
Acknowledgements
We would like to thank the Mathematisches Forschungsinstitut Oberwolfach for the kind hospitality and for inspiring this work.
M. Annunziato would like to thank the support by the European Science Foundation Exchange OPTPDE Grant.
A. Borzì acknowledges the support of the European Union Marie Curie Research Training Network “Multi- ITN STRIKE-Novel Methods in Computational Finance”.
R. Tempone is a member of the KAUST SRI Center for Uncertainty Quantification in Computational Science and Engineering.
F. Nobile acknowledges the support of CADMOS (Center for Advances Modeling and Science).
Funding
Supported in part by the European Union under Grant Agreement “Multi-ITN STRIKE-Novel Methods in Com- putational Finance”. Fund Project No. 304617 Marie Curie Research Training Network.