Existence and Uniqueness of Positive Solutions for Fourth-Order Nonlinear Singular Sturm-Liouville Problems

Ying He

School of Mathematics and Statistics, Northeast Petroleum University, Daqing, China.

DOI: 10.4236/jamp.2014.29099                

Abstract

By mixed monotone method, we establish the existence and uniqueness of positive solutions for fourth-order nonlinear singular Sturm-Liouville problems. The theorems obtained are very general and complement previously known results.

Keywords

Mixed Monotone Operator, Fourth-Order Boundary Value Problem, Singular, Uniqueness

1. Introduction

Boundary value problems for ordinary differential equations are used to describe a large number of physical, biological and chemical phenomena. Many authors studied the existence and multiplicity of positive solutions for the boundary value problem of fourth-order differential equations (see [1] [2] and their references). In particular, the singular case was considered (see [3] [4] ). They mainly concern with the existence and mul- tiplicity of solutions using different methods. Recently, there were a few articles devoted to uniqueness problem by using the mixed monotone fixed point theorem (see [5] ). However, they mainly investigated the case 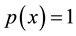and. Motivated by the work mentioned above, this paper attempts to study the existence and uniqueness of solutions for the more general Sturm-Liouville boundary value problem, i.e. 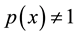and.

In this paper, first we get a unique fixed point theorem for a class of mixed monotone operators. Our idea comes from the fixed point theorems for mixed monotone operators (see [6] ). In virtue of the theorem, we consider the following singular fourth-order boundary problem:

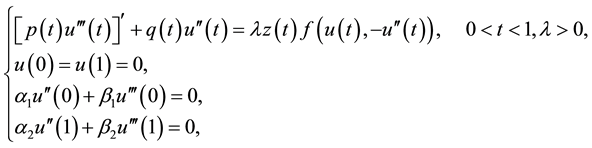(1.1)

Throughout this paper, we always suppose that

Moreover, 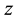may be singular at or, and 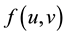may be singular at.

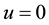2. Preliminary

Let 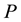be a normal cone of a Banach space, and with,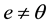. Define

Now we give a definition (see [5] ).

Definition 2.1 Assume. is said to be mixed monotone if is nondecreasing in and nonincreasing in, i.e. if implies for any, and implies for any. is said to be a fixed point of if.

Theorem 2.1 Suppose that is a mixed monotone operator and a constant, , such that

(2.1)

Then has a unique fixed point. Moreover, for any,

satisfy

where

, is a constant from.

Theorem 2.2 (see [5] ): Suppose that is a mixed monotone operator and a constant such that (2.1) holds. If is a unique solution of equation

in, then,. If, then implies, , and

3. Uniqueness Positive Solution of Problem (1.1)

This section discusses the problem

Throughout this section, we assume that

(3.1)

where

(3.2)

Let and We denote the Green’s functions for the following boundary value problems

and

by and, respectively. It is well known that and can be written by

and

Lemma 3.1 Suppose that holds, then the Green’s function, possesses the following pro- perties:

1): is increasing and,.

2): is decreasing and,.

3):.

4):.

5): is a positive constant. Moreover,.

6): is continuous and symmetrical over.

7): has continuously partial derivative over,.

8): For each fixed, satisfies for,. Moreover, for.

9): has discontinuous point of the first kind at and

Following from Lemma, it is easy to see that

1)

2)

Let, and define an integral operator by

.

Then, we have

Lemma 3.2 The boundary value problem (1) has a positive solution if only if the integral-differential boundary value problem

(3.3)

has a positive solution .Define an operator by

Clearly is a solution of BVP Equation (3.3) if and only if is a fixed point of the operator.

Let Obviously, is a normal cone of Banach space.

Theorem 3.1 Suppose that there exists such that

(3.4)

(3.5)

for any and, and satisfies

(3.6)

Then Equation (3.3) has a unique positive solution which is unique in, In addition Equation (1.1) has a positive solution which is unique in.

Proof Since (3.5) holds, let, one has

then

(3.7)

Let. The above inequality is

(3.8)

From (3.5), (3.7) and (3.8), one has

(3.9)

Similarly, from (3.4), one has

(3.10)

Let,. one has

(3.11)

Let. It is clear that and now let

(3.12)

where is chosen such that

(3.13)

Note for any, we have

and

Then from (3.7)-(3.11) we have for,

(3.14)

and

(3.15)

For any, we define

(3.16)

First we show that. Then from (3.14) we have

Thus, from (3.15), we have

So, is well defined and.

Next, for any, one has

So the conditions of Theorems 2.1 and 2.2 hold. Therefore there exists a unique such that. It is easy to check that is a unique positive solution of Equation (3.3) in for given. Now using Lemma 3.2 we see that is a positive solution of (1.1) which is unique in for a given (to see this note if is another solution fo (1.1) in then for some and note since then is a solution of (3.3) so from above so). This completes the proof of Theorem 3.1.

Example Consider the following singular fourth-order boundary value problem:

where, and satisfies.

Let

Thus and for any , ,

Now Theorem 3.1 guarantees that the above equation has a positive solution.

Funding

Project supported by Heilongjiang province education department natural science research item, China (12541076).

Conflicts of Interest

The authors declare no conflicts of interest.

References

[1]	Jiang, D.Q., Liu, H. and Xu, X. (2005) Nonresonant Singular Fourth-Order Boundary Value Problems. Applied Mathematics Letters, 18, 69-75. http://dx.doi.org/10.1016/j.aml.2003.05.016
[2]	Jiang, D.Q. (2000) Multiple Positive Solutions to Singular Boundary Value Problems for Superlinear Higher Order ODEs. Computers Mathematics with Applications, 40, 249-259. http://dx.doi.org/10.1016/S0898-1221(00)00158-9
[3]	Kong, L. and Wang, J. (2001) The Green’s Function for (k,n-k) Conjugate Boundary Value Problems and Its Applications. Journal of Mathematical Analysis and Applications, 255, 404-422. http://dx.doi.org/10.1006/jmaa.2000.7158
[4]	Liu, Y. (2003) Structure of a Class of Singular Boundary Value Problem with Superlinear Effect. Journal of Mathematical Analysis and Applications, 284, 64-75. http://dx.doi.org/10.1016/S0022-247X(03)00214-2
[5]	Liu, Y. (2004) Multiple Positive Solutions of Nonlinear Singular Boundary Value Problem for Fourth Order Equations. Applied Mathematics Letters, 17, 747-757. http://dx.doi.org/10.1016/j.aml.2004.06.001
[6]	Guo, D. (2000) The Order Methods in Nonlinear Analysis. Shandong Technology and Science Press, Jinan.