A Study of Multifractal Spectra and Renyi Dimensions in 14.5A GeV/c 28Si-Nucleus Collisions ()
1. Introduction
Fluctuations of dynamical nature were observed for the first time in the JACEE event [1] having unusually very high multiplicity. The study of non-statistical fluctuations has since then attracted a great deal of attention of high energy physicists due to possibility of disentangling some important information about the mechanism of multiparticle production in relativistic hadronic and nuclear collisions. It has been observed [2] [3] that large particle density fluctuations in small rapidity bins exhibit self-similar behaviour. However, the origin of multifractality still remains largely unexplained. Self-similar behaviour of particles produced is closely linked to multifractality, which is a consequence of cascading mechanism of particle production in these collisions. Power-law behaviour of Scaled Factorial Moments indeed exhibits fractal patterns [4] [5] in the multiparticle dynamics of the final state of the collisions. Therefore, the issue of self-similarity under the perspective of fractal properties of the hadronic matter in multiparticle production needs to be adequately addressed. To investigate quantitatively any single particle density distribution in the framework of multifractal characteristics, a method has been developed [6] . This method has been successively applied in studying intermittent behaviour of particle density distributions over a wide range of pseudorapidity bin widths. In the present study, an attempt is made to investigate multifractal characteristics of the secondary particles produced in 14.5A GeV/c 28Si-nucleus collisions.
2. Mathematical Formalism
In order to investigate various interesting features of multifractal moments in a given pseudorapidity range, 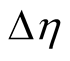 ,
,  , is divided into
, is divided into  bins of width
bins of width . As some of the bins may be empty, the number of non-empty bins is represented by
. As some of the bins may be empty, the number of non-empty bins is represented by . According to Hwa [6] , mutltifractal moments,
. According to Hwa [6] , mutltifractal moments,  are defined as:
are defined as:
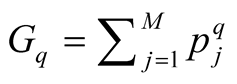 (1)
(1)
where  , such that
, such that  and
and  denotes the number of particles
denotes the number of particles  bin. Here
bin. Here  represents a real number, both positive and negative. The summation is performed over only non-empty bins and vertical average of horizontal moments is calculated from:
represents a real number, both positive and negative. The summation is performed over only non-empty bins and vertical average of horizontal moments is calculated from:
 (2)
(2)
where  stands for the total number of events in a given data sample. If there occurs self-similarity in the production of particles,
stands for the total number of events in a given data sample. If there occurs self-similarity in the production of particles,  moments can be expressed in the form of a power-law as:
moments can be expressed in the form of a power-law as:
 (3)
(3)
where 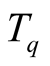 are the mass exponents and may be determined from the observed linear dependence of
are the mass exponents and may be determined from the observed linear dependence of  on
on  using Equation (3). The multifractal spectrum function,
using Equation (3). The multifractal spectrum function,  , and Renyi dimensions,
, and Renyi dimensions,  , are, therefore, used to examine fractal nature of particle emitting source in the analysis of the data. The Renyi dimensions are sometimes referred to as generalized dimensions. For nuclear collisions,
, are, therefore, used to examine fractal nature of particle emitting source in the analysis of the data. The Renyi dimensions are sometimes referred to as generalized dimensions. For nuclear collisions, 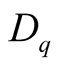 are related to the slope parameter,
are related to the slope parameter, 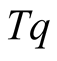 , as [5] :
, as [5] :
 (4)
(4)
However,  ,
, 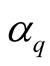 and
and  may be related in the following function:
may be related in the following function:
 (5)
(5)
and
 (6)
(6)
3. Experimental Details
In the present study a stack of ILFORD G5 emulsion exposed to 14.5A GeV/c 28Si nuclei from AGS, BNL has been used. A random sample of 555 interactions with , where
, where  represents the number of charged particles produced in an interactions with relative velocity,
represents the number of charged particles produced in an interactions with relative velocity,  , is analyzed. In order to compare the experimental results with the corresponding values predicted by Lund Monte Carlo Model, FRITIOF, 5000 events with the same descriptions generated by FRITIOF, are also analyzed. For studying target mass dependence of various important parameters linked to multifractality, the given sample of collisions is divided in three categories: 1) of interactions due to CNO group; 2) interactions due to AgBr group and 3) entire sample.
, is analyzed. In order to compare the experimental results with the corresponding values predicted by Lund Monte Carlo Model, FRITIOF, 5000 events with the same descriptions generated by FRITIOF, are also analyzed. For studying target mass dependence of various important parameters linked to multifractality, the given sample of collisions is divided in three categories: 1) of interactions due to CNO group; 2) interactions due to AgBr group and 3) entire sample.
4. Results and Discussion
The slope parameter,  , for the linear region of the
, for the linear region of the  versus
versus  plot for each data set is calculated and plotted as a function of
plot for each data set is calculated and plotted as a function of  in Figure 1. It may be seen from the figure that
in Figure 1. It may be seen from the figure that  increases significantly with increasing
increases significantly with increasing  for
for , whereas it is observed to flatten with increasing
, whereas it is observed to flatten with increasing  for
for . The Renyi dimensions,
. The Renyi dimensions, 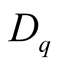 , and multfractal spectral function,
, and multfractal spectral function,  , are calculated using Equations (2)-(4) for both the experimental and FRITIOF data. Shown in Figure 2 and Figure 3 are
, are calculated using Equations (2)-(4) for both the experimental and FRITIOF data. Shown in Figure 2 and Figure 3 are  versus
versus  and
and  versus
versus 
plots for the experimental and FRITIOF data. It is clear from Figure 2 that Renyi dimensions,  , decrease with increasing order of the moments,
, decrease with increasing order of the moments,  , from −6 to 6, which indicates the presence of multifractality in multiparticle production in 14.5A GeV/c 28Si-nucleus collisions.
, from −6 to 6, which indicates the presence of multifractality in multiparticle production in 14.5A GeV/c 28Si-nucleus collisions.
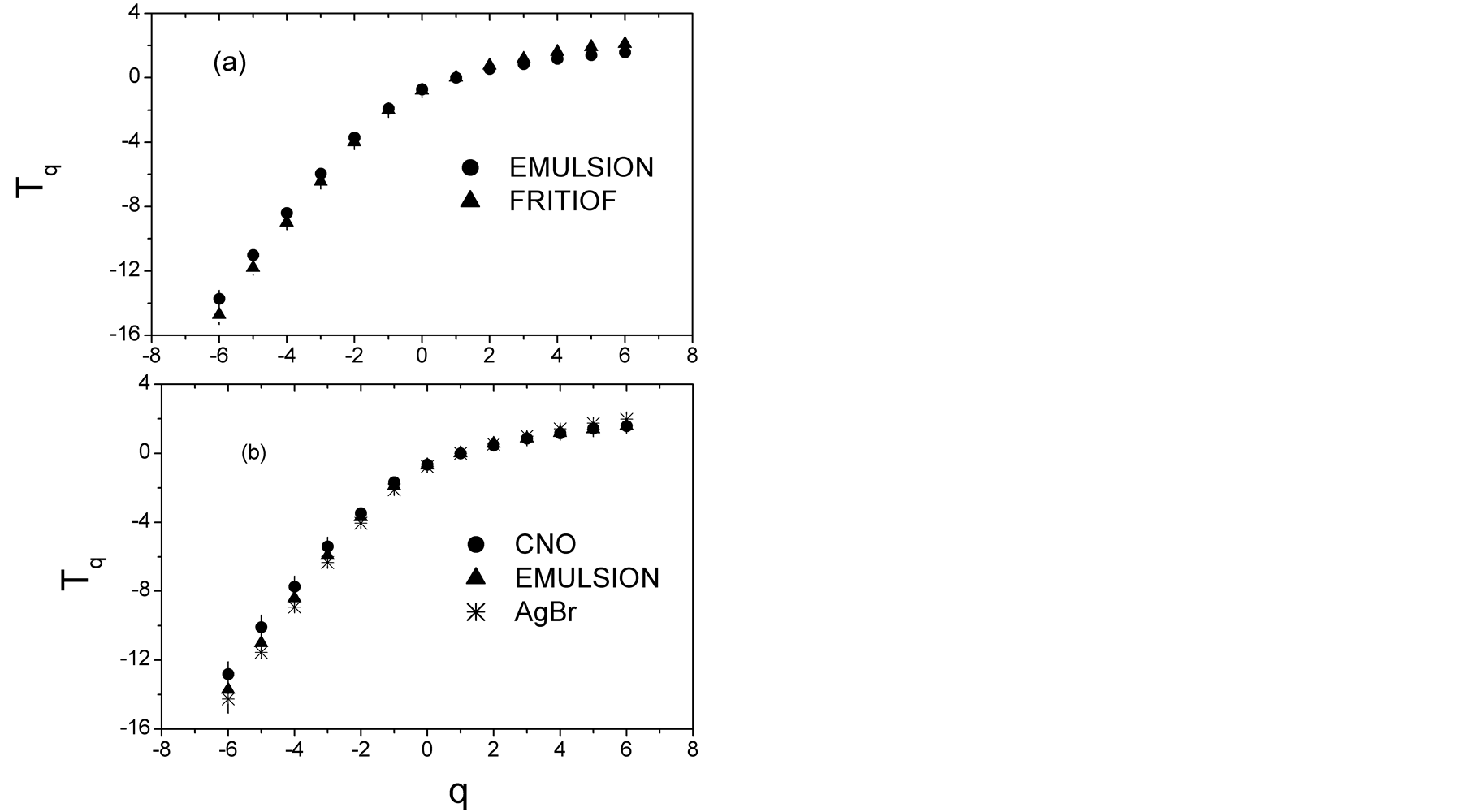
Figure 1. Variations of  with
with  in 14.5A GeV/c 28Sinucleus collisions.
in 14.5A GeV/c 28Sinucleus collisions.

Figure 2. Variations of 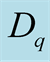 with
with  in 14.5A GeV/c 28Si-nucleus collisions for the experimental and FRITIOF generated events.
in 14.5A GeV/c 28Si-nucleus collisions for the experimental and FRITIOF generated events.

Figure 3. Variations of  with
with  in 14.5A GeV/c 28Sinucleus collisions for the experimental and FRITIOF generated events.
in 14.5A GeV/c 28Sinucleus collisions for the experimental and FRITIOF generated events.
Variations of multifractal spectral function,  , with
, with  for the FRITIOF and experimental data are displayed in Figure 3. It is seen from the figure that the value of Spectral Function,
for the FRITIOF and experimental data are displayed in Figure 3. It is seen from the figure that the value of Spectral Function,  , lies between
, lies between
−2.48 and 0.71 and −2.68 and 0.79 for the experimental and FRITIOF generated data respectively. The spectra are concave downwards centered around  corresponding to
corresponding to .
.
In order to examine whether Renyi dimensions, 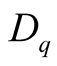 and Multifractal Spectral Function
and Multifractal Spectral Function , depend on target mass,
, depend on target mass,  and
and 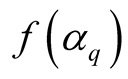 are plotted as a function of
are plotted as a function of  and
and  respectively for the interactions of 14.5 A GeV/c 28Si nuclei with CNO, emulsion and AgBr targets and are shown in Figure 4 and Figure 5 respectively. Renyi dimensions are found to be relatively higher for the interactions due to heavier targets for each order of the moments. Although the effect appears to be rather more pronounced for
respectively for the interactions of 14.5 A GeV/c 28Si nuclei with CNO, emulsion and AgBr targets and are shown in Figure 4 and Figure 5 respectively. Renyi dimensions are found to be relatively higher for the interactions due to heavier targets for each order of the moments. Although the effect appears to be rather more pronounced for . One of the possible reasons for Renyi dimensions being higher for the interactions due to heavier targets may be attributed to the fact that average multiplicity increases with increasing target size.
. One of the possible reasons for Renyi dimensions being higher for the interactions due to heavier targets may be attributed to the fact that average multiplicity increases with increasing target size.
From  versus
versus  plot one may come to the following important conclusions:
plot one may come to the following important conclusions:
1. In each case, Multifractal Spectral Function,  , is represented by a continuous curve, thus characterizing a quantitative manifestation of the fluctuations in the rapidity space.
, is represented by a continuous curve, thus characterizing a quantitative manifestation of the fluctuations in the rapidity space.
2. The spectra are concave downwards in shape. However, for none of the two data sets, the spectrum has sharp peak, indicating thereby that pseudorapidity density distribution is not smooth.
3. The value of 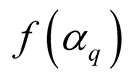 is relatively smaller for the targets of higher mass and the spectrum tends to become wider with increasing target size.
is relatively smaller for the targets of higher mass and the spectrum tends to become wider with increasing target size.
The  spectrum may be used to estimate Renyi dimensions,
spectrum may be used to estimate Renyi dimensions,  , which is the basic characteristics of any fractal structure. The values of
, which is the basic characteristics of any fractal structure. The values of  are estimated [5] -[7] using:
are estimated [5] -[7] using:
 (7)
(7)
The values of Renyi’s dimensions, 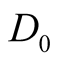 ,
, and
and  , which are regarded to be the most sensitive to the production mechanism, are calculated for the experimental and FRITIOF simulated data. The values of
, which are regarded to be the most sensitive to the production mechanism, are calculated for the experimental and FRITIOF simulated data. The values of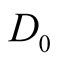 ,
,  and
and  are presented in Table1 It may be seen from the table that values of
are presented in Table1 It may be seen from the table that values of ,,
,, 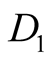 and
and  compare fairly well with the corresponding results obtained for the FRITIOF generated data.
compare fairly well with the corresponding results obtained for the FRITIOF generated data.
5. Conclusion
From the analysis of 14.5A GeV/c 28Si-nucleus collisions performed in terms of multifractal moments,  , Multifractal Spectral Function,
, Multifractal Spectral Function, 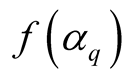 , when plotted against
, when plotted against , is observed to be concave in shape with a maximum occurring at around
, is observed to be concave in shape with a maximum occurring at around  at
at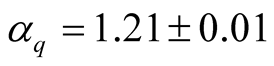 . Furthermore,
. Furthermore,  in the entire
in the entire

Figure 4. Variations of  with
with  in 14.5A GeV/c 28Si-nucleus collisions for various targets.
in 14.5A GeV/c 28Si-nucleus collisions for various targets.

Figure 5. Variations of  with
with  in 14.5A GeV/c 28Sinucleus collisions for various targets.
in 14.5A GeV/c 28Sinucleus collisions for various targets.

Table 1. Values of Renyi dimensions,  , in 14.5 A GeV/c 28Si-nucleus collisions for
, in 14.5 A GeV/c 28Si-nucleus collisions for  and 2.
and 2.
pseudorapidity space manifests self-similarity. The decreasing trend in the values of  with increasing
with increasing  confirms the presence of multifractality in the collisions considered in the present study. Weak target mass dependence of
confirms the presence of multifractality in the collisions considered in the present study. Weak target mass dependence of .and
.and  is revealed. Finally, Renyi dimensions,
is revealed. Finally, Renyi dimensions,  ,
, 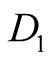 and
and , obtained for the experimental data are found to be in excellent agreement with the corresponding values for the FRITIOF generated events. It may be remarked that, a similar study of nuclear interactions at still higher energies, including RHIC and LHC, may provide invaluable information regarding the mechanism of multiparticle production.
, obtained for the experimental data are found to be in excellent agreement with the corresponding values for the FRITIOF generated events. It may be remarked that, a similar study of nuclear interactions at still higher energies, including RHIC and LHC, may provide invaluable information regarding the mechanism of multiparticle production.
NOTES
*Corresponding author.