Theory and Application of Numerical Simulation of Chemical Flooding in High Temperature and High Salt Reservoirs ()
1. Introduction
At present an effective method, water-flooding, to keep the pressure of reservoirs is popular in the world, and the recovery efficiency is more outstanding than any other natural exploring forms. It gives more benefits and helps Chinese oil fields keep high quantity production. It continues to be more important and a strategic job to develop the exploiting efficiency of crude oil in the way water-flooding driving.
Much crude oil remains in the reservoir after water-flooding exploiting, which stays underground due to the constraint of capillary force, or doesn’t move due to slight influenced region and the fluidity ratio between displacement phase and driven phase. How to develop the displacement efficiency? A popular method considered is that the injected mixture includes chemical addition agents such as polymer, surface active agent and alkali. Polymer can optimize the fluidity of displacement phase, modify the ratio with respect to driven phases, balance the leading edges well, weaken the inner porous layer, and increase the efficiency of displacement and the pressure gradient. Surface active agent and alkali can decrease interfacial tensions of different phases, then make the bounded oil move and gather. Some hypotheses should be made for the mathematical models. Local thermodynamic equilibrium holds in the reservoir, solid phase has no motion, and the rock and mixture fluid are slight- compressible, of Fick dispersion, ideal and suitable for Darcy Law.
The equilibrium equation of multi-phase, multi-components and slight compressible mixture is formulated by a nonlinear coupled system of partial differential equations. It is hard to solve this system because many modern numerical methods such as mixed element, finite element, finite difference and numerical algebra, will be involved in the simulation. In general speaking, based on physical means the pressure function is solved by an implicit scheme and the concentration values are obtained by an explicit solver or an implicit solver. The scholars try to find good ways analyzing the data and numerical results and doing some research work in simulation, which describe the whole process of chemistry displacements very well and help the engineers control the rules and process of displacement and forecast the recovery efficiency of natural oil and compute the oil percentage of output liquid and the percent of polymer and surface active agent. By numerical research the curves describing different components motion are shown, and some plans are made about the beginning and end of injected liquid and some related parameters of natural oil efficiency are derived. These conclusions, important techniques in chemistry displacements, can be used in forecasting the characters of fields, choosing different optimization plans, establishing the models of chemical displacements of reservoir, completing computational software and carrying out the numerical simulation. Petroleum engineers and mathematicians pay more attention to modern new techniques of exploiting natural oil.
Yuan visited United States and accomplished some work cooperate with Prof. R. E. Ewing during 1985 to 1988, and kept a series of research in theoretical analysis and applications of numerical simulation. With the leading of Yuan several research groups undertook some important projects from 1991 to 1995 such as “Eighth- Five” national key science and technology program (the Program for Tackling Key Programs) (85-203-01-087) entitled “research and application of the polymer displacement software” [1] -[6] . The software was applied in designing plan and research work of polymer displacements in industrial production region of Daqing Oilfield. Many conclusions from actual numerical results are illustrated such as effects of fragments, fragments setting of rinsing protection, quantity of polymer, and used in actual simulations which give rise to outstanding economic and social benefits [7] - [9] . Later the authors undertook a key tackling program of oil administration of Daqing Oilfield (DQYJ-1201002-2006-JS-9565)—solving development of mathematical models and completing explain of reservoir [10] . This software system is also applied in three compound combination flooding of Gudong Little Well experimental region of Shengli Oilfield, polymer flooding of Gudong Middle One experimental region, optimization of combination flooding expanded experimental region of Gudong West region and feasibility of active water flooding of Gudong eighth region, and many interesting results are obtained [11] .
Theory, method and application of numerical simulation are studied for high temperature, high salt, complicated geology and large-scale reservoirs and the principle of chemical flooding in this paper. Based on the former research, the conclusions and more discussion of the national major special project on science and technology (2008ZX05011-004) “Study on key technology of chemical flooding numerical simulation in high temperature and high salt reservoirs (on numerical simulation)” are given, which consists of permeation fluid mechanical models of numerical simulation of high temperature and high salt polymer flooding and compound combination flooding, numerical methods, applicable software, theoretical analysis and applications in oilfields.
2. Mathematical Model of Polymer Flooding and Compound Combination Flooding
This section includes five subsections: Section 2.1, basic hypothesis, Section 2.2, conservation equation of matter, Section 2.3, the pressure equation, Section 2.4, the concentration equation, Section 2.5, the concentration equation of chemical components.
2.1. Basic Hypothesis
Mathematical model of polymer flooding and compound combination flooding is derived under the following hypothesis. Local thermodynamic equilibrium holds in the reservoir, solid phase doesn’t motion, rock and mixture fluid are slight-compressible, of Fick dispersion, ideal and suitable for Darcy Law [1] -[3] [7] -[10] .
2.2. Conservation Equation of Matter
Under the primary hypothesis, a conservation equation of the 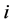 -th component is stated as follows dependent of the
-th component is stated as follows dependent of the 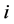 -th concentration
-th concentration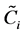 :
:
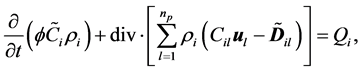 (1)
(1)
where  represents the concentration the concentration of the i-th component in the
represents the concentration the concentration of the i-th component in the  -phase,
-phase,  means source sink term,
means source sink term, 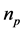 means the number of phases, and subscripts
means the number of phases, and subscripts 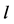 denotes the order of phases. The symbol
denotes the order of phases. The symbol 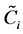 represents the total concentration of the
represents the total concentration of the 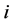 -th component, i.e. the summation of concentrations of the
-th component, i.e. the summation of concentrations of the 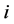 -th component in different phases (including adsorbed phase):
-th component in different phases (including adsorbed phase):
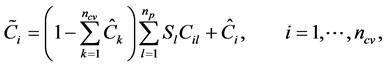 (2)
(2)
where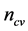 , the number of component whose volume couldn’t be ignored, and
, the number of component whose volume couldn’t be ignored, and 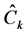 denotes the adsorption concentration of the component
denotes the adsorption concentration of the component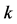 .
.
The density of the 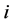 -th component is dependent of the pressure
-th component is dependent of the pressure  under slight compressible case:
under slight compressible case:
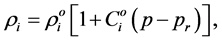 (3)
(3)
where 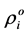 is the density of the
is the density of the 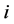 -th component under considering reference pressure
-th component under considering reference pressure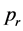 , and
, and 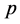 means the pressure and
means the pressure and 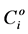 is the coefficient of compressibility of the
is the coefficient of compressibility of the 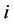 -th component.
-th component.
Suppose that the rock is compressible, then the function of the porosity 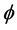 and the pressure is
and the pressure is
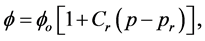 (4)
(4)
where 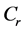 means the coefficient of compressibility of the rock.
means the coefficient of compressibility of the rock.
Darcy velocity, 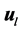 , is described by Darcy Law,
, is described by Darcy Law,
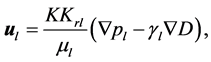 (5)
(5)
where 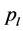 means the pressure of phases,
means the pressure of phases, 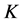 is the permeability tensor,
is the permeability tensor, 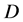 is the depth,
is the depth, 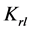 is the relative permeability,
is the relative permeability, 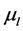 is the viscosity and
is the viscosity and 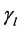 is the proportion.
is the proportion.
The dispersion flux is expressed in the following Fick formation:
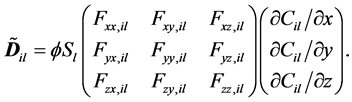 (6)
(6)
The dispersion tensor , including molecular diffusion
, including molecular diffusion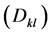 , can be formulated as
, can be formulated as
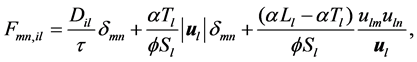 (7)
(7)
where 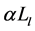 and
and  denote the longitudinal and the lateral dispersion parameters of the
denote the longitudinal and the lateral dispersion parameters of the 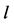 -th phase,
-th phase,  is the tortuosity,
is the tortuosity,  and
and 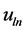 are the components, and
are the components, and 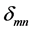 means Kronecher Delta. The net flow of each phase is:
means Kronecher Delta. The net flow of each phase is:
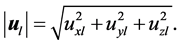 (8)
(8)
2.3. The Pressure Equation
Considering all the conservative equations of each matter with positive volume together, using Darcy Law and capillary pressure to express the flux and the pressure relations of different phases respectively, and combining with the following constraints
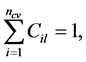 (9)
(9)
We can get the pressure equation of referenced phase:
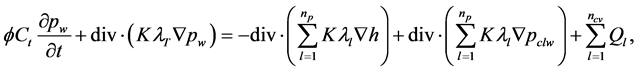 (10)
(10)
where
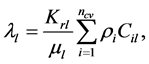 (11)
(11)
and the total relative fluidity 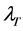 is
is
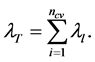 (12)
(12)
The total coefficient of compressibility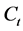 , is a function dependent of the compressibility of rocks
, is a function dependent of the compressibility of rocks  and components of the mixture
and components of the mixture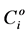 :
:
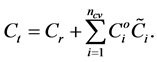
2.4. The Concentration Equation
Let 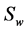 and
and 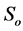 be concentrations of water phase and oil phase denoted by subscripts
be concentrations of water phase and oil phase denoted by subscripts 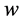 and
and 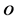 denote and the relation
denote and the relation  holds obviously. The equations on concentrations of water and oil phases are expressed as follows by conservation of the mass (1)
holds obviously. The equations on concentrations of water and oil phases are expressed as follows by conservation of the mass (1)
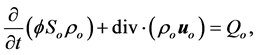 (13)
(13)
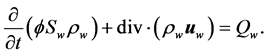 (14)
(14)
By Darcy Law the velocities of different phases are derived by
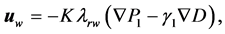 (15)
(15)
 (16)
(16)
where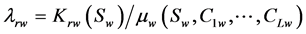 ,
, 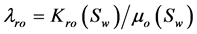 are the fluidities of two phases, and
are the fluidities of two phases, and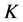 ,
, 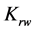 and
and 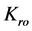 are the absolute permeability tensor, relative permeabilities.
are the absolute permeability tensor, relative permeabilities. 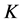 is the absolute permeability of medium, and
is the absolute permeability of medium, and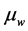 ,
,  are the viscosities of water-oil phases dependent on their concentrations and the saturations of polymer and the two opposing principles in nature.
are the viscosities of water-oil phases dependent on their concentrations and the saturations of polymer and the two opposing principles in nature.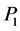 ,
, 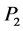 and
and ,
, 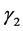 respectively denote the pressures and the densities of water phase and oil phase and
respectively denote the pressures and the densities of water phase and oil phase and 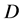 is the depth function,
is the depth function,
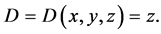
2.5. The Concentrations of Chemical Substance Components
Note that all the components (polymer and different principles) are mixed in the water phase and no transmission takes place, then
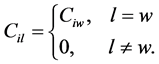 (17)
(17)
Substitute (17) into (1),
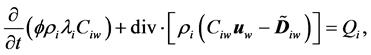 (18)
(18)
where 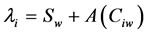 and
and  is dependent of the absorptions.
is dependent of the absorptions.
3. Numerical Methods
This section consists of three subsections: Section 3.1 solving the pressure equation, Section 3.2 solving the concentration equation, and Section 3.3 structuring a numerical algorithm of components.
3.1. Solving the Pressure
Let the parameters with subscripts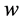 ,
,  be related with the water and the oil respectively, such as
be related with the water and the oil respectively, such as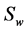 ,
, 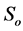 and
and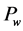 ,
, 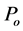 denote the saturations and the pressures of water and oil phases. Note that the mixture fluid is only made by oil and water two phases in the model of polymer flooding and compound combination flooding and we can describe the pressure in a simple formula
denote the saturations and the pressures of water and oil phases. Note that the mixture fluid is only made by oil and water two phases in the model of polymer flooding and compound combination flooding and we can describe the pressure in a simple formula
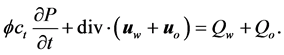 (19)
(19)
Using Darcy Law and the formula of capillary force, we rewrite the above equation as follows with respect to an unknown variable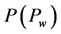 ,
,
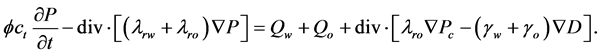 (20)
(20)
The initial values of the saturations are known at the beginning of simulations while the pressure values should be initialized in the following process. When the pressure  at the
at the 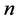 -th time step are known, then the flow velocities are obtained and the values of the saturation and components at the next step
-th time step are known, then the flow velocities are obtained and the values of the saturation and components at the next step 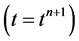 are computed. The pressure, denoted by a parabolic equation, is obtained by a seven-point central difference method. Considering the physical features of two-phase we assign
are computed. The pressure, denoted by a parabolic equation, is obtained by a seven-point central difference method. Considering the physical features of two-phase we assign 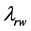 and
and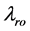 , the values of the left-side term, in accordance with upstream principles. At the injected wells and produced wells with fixed quantities, the right source term can be assigned directly and the values of quantity are determined by the difference between the pressure of local regions and the pressure of bottom holes at injected wells and produced wells with fixed pressures. The production quantities of different phases are distributed by the relative fluidity of oil-water phases. In addition, the pressure equation is degraded into an equation of elliptic type, and the matrix is not strictly diagonal-dominated under an impressible assumption (the coefficients of compressibility are assumed to be zero). In the way of taking the diagonal unit be 1 and non-diagonal units be zero, the equation of feature edges is consistent with the equation of normal oil deposits. The data in feature edges don’t need to be replaced by the values of solutions, which makes the quantity of physical data as a constant in the computation. If the program (necessary for the design) runs at feature edges virtual data will be used in the whole computation.
, the values of the left-side term, in accordance with upstream principles. At the injected wells and produced wells with fixed quantities, the right source term can be assigned directly and the values of quantity are determined by the difference between the pressure of local regions and the pressure of bottom holes at injected wells and produced wells with fixed pressures. The production quantities of different phases are distributed by the relative fluidity of oil-water phases. In addition, the pressure equation is degraded into an equation of elliptic type, and the matrix is not strictly diagonal-dominated under an impressible assumption (the coefficients of compressibility are assumed to be zero). In the way of taking the diagonal unit be 1 and non-diagonal units be zero, the equation of feature edges is consistent with the equation of normal oil deposits. The data in feature edges don’t need to be replaced by the values of solutions, which makes the quantity of physical data as a constant in the computation. If the program (necessary for the design) runs at feature edges virtual data will be used in the whole computation.
Given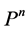 , using upstream seven-point central difference algorithm to compute
, using upstream seven-point central difference algorithm to compute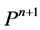 ,
,
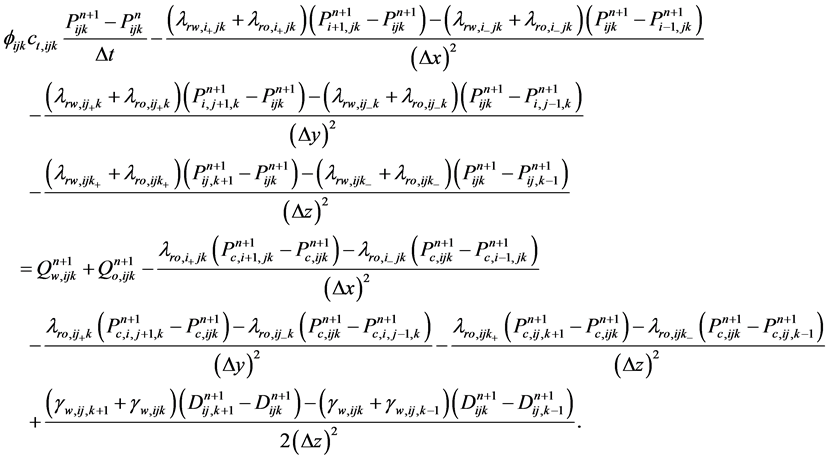 (21)
(21)
The subscript denotes the upstream position in the first direction between the 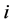 -th point and the
-th point and the 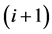 -th point. An assumption is given that there is no flow moving through the boundary. That is to say that its boundary condition is homogeneous of Neumann type. The quantities at the injected wells
-th point. An assumption is given that there is no flow moving through the boundary. That is to say that its boundary condition is homogeneous of Neumann type. The quantities at the injected wells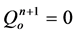 ,
, 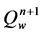 are known and those at the produced wells
are known and those at the produced wells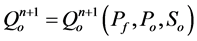 ,
, 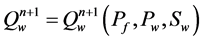 are given implicitly by the flowing bottom hole pressure
are given implicitly by the flowing bottom hole pressure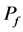 , the pressures of phases and the relative mobility ratio. Distributed quantities are computed by an allocation program after the pressure values are obtained. It is easy to solve the saturation equation when the values of source and sink terms.
, the pressures of phases and the relative mobility ratio. Distributed quantities are computed by an allocation program after the pressure values are obtained. It is easy to solve the saturation equation when the values of source and sink terms.
3.2. Solving the Saturation
Using upstream order, implicit upwind Newton iteration to solve the saturation of water phase, then the values of oil saturation 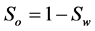 are computed. The saturation of water phase is described by
are computed. The saturation of water phase is described by
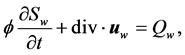
or expressed in another form combined with Darcy Law
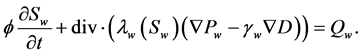 (22)
(22)
The pressure of water phase 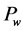 at
at 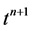 and the quantity
and the quantity 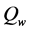 are known, then the saturation of water
are known, then the saturation of water 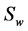 at
at 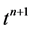 are computed by the following discrete algorithm,
are computed by the following discrete algorithm,
 (23)
(23)
where the subscript 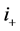 denotes the upstream position according to the moving trend between
denotes the upstream position according to the moving trend between 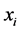 and
and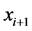 , i.e. it is either
, i.e. it is either 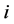 or
or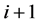 . It is hard to solve the nonlinear equations directly.
. It is hard to solve the nonlinear equations directly. 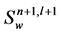 at the
at the  iteration step is obtained by Newton iteration under taking the value at the previous step as the initial condition
iteration step is obtained by Newton iteration under taking the value at the previous step as the initial condition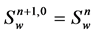 . Note the following Taylor expansion,
. Note the following Taylor expansion,
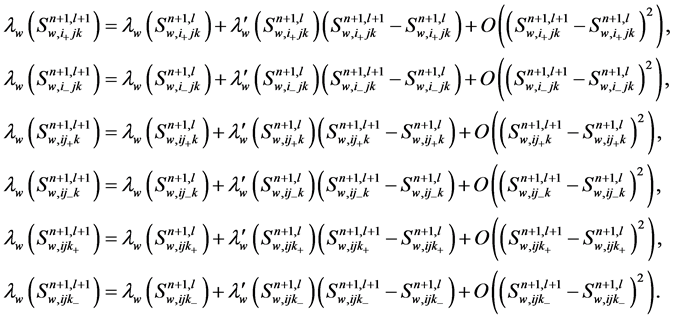
Delete the remainder truncation, substitute the approximation expressions into the difference algorithm, take 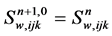 as iteration initial conditions and obtain the iteration values
as iteration initial conditions and obtain the iteration values 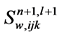 at the
at the 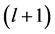 -th step by solving the following linear equations
-th step by solving the following linear equations
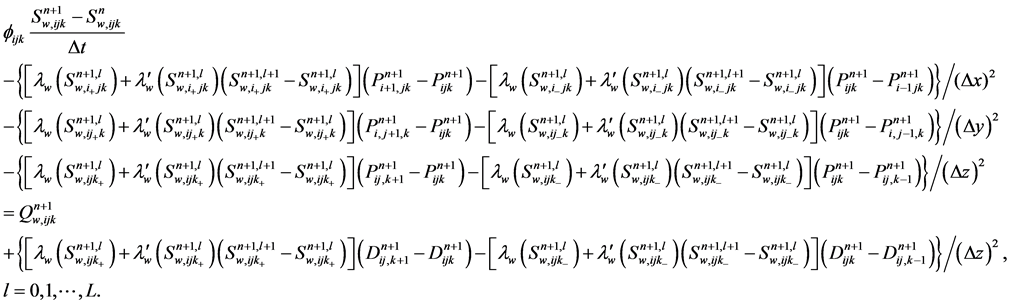 (24)
(24)
The program runs based on upstream sequence rule, and the iteration value at the 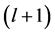 -th step is computed until the relative error meets a designed requirement or the iteration reaches the steps when the values at upstream points are known. The final iterative value is denoted by
-th step is computed until the relative error meets a designed requirement or the iteration reaches the steps when the values at upstream points are known. The final iterative value is denoted by .
.
3.3. Numerical Algorithm of Concentration Components
The components of water phase keep conservation of the mass of anions, cations and molecules and other particles, whose equation is of diffusion-convection and convection dominated. It has more strengths such as high order of accuracy and high efficiency of simulation applying decomposition of operators into the nonlinear system and solving two subproblems: a hyperbolic equation of convection type and a diffusion equation. The former is solved implicitly by an upwind method, which can be carried out explicitly by an upstream technique. The latter is solved by alternating directions finite difference method, which can improve the computational speed. The concentration equation of 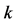 -component, a typical convection-diffusion equation, is simplified as follows
-component, a typical convection-diffusion equation, is simplified as follows
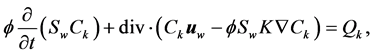 (25)
(25)
where the dispersion tensor is a diagonal form. Given the saturation 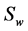 and the flow field
and the flow field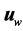 , the concentration
, the concentration 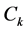 is to be computed by using an implicit upwind method to solve a convection problem, where the subscript k is ignored and C denotes a component concentration.
is to be computed by using an implicit upwind method to solve a convection problem, where the subscript k is ignored and C denotes a component concentration.
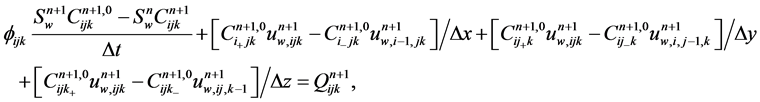 (26)
(26)
The values 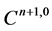 is obtained, then the diffusion equation is discretized alternatively in three directions. In x-direction,
is obtained, then the diffusion equation is discretized alternatively in three directions. In x-direction,
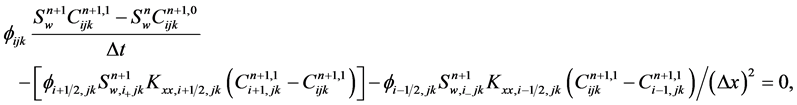 (27a)
(27a)
Then in 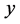 -direction,
-direction,
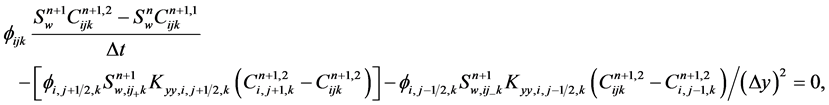 (27b)
(27b)
At last in 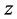 -direction,
-direction, 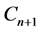 is obtained,
is obtained,
 (27c)
(27c)
Then the discrete solutions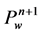 ,
, 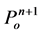 ,
, 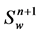 ,
, 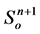 ,
, 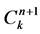 are obtained and the computation runs in the next step.
are obtained and the computation runs in the next step.
3.4. Viscosity Computation of High Temperature and High Salt Reservoir
The polymer hydrolysis can decrease the viscosity in the high temperature and high salt reservoirs, and the viscosity is different under different polymers. The viscosity is computed by
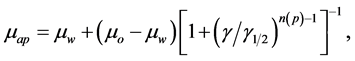 (28)
(28)
where the values of parameters are defined as follows,
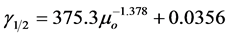 ,
, 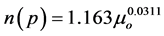 ,
, 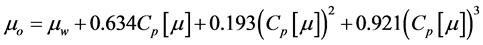 ,
, 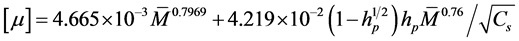 .
. 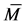 denotes the average molecular weight of
denotes the average molecular weight of
polymer, and 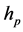 denotes the degree of hydrolysis of the polymer with decimal unit.
denotes the degree of hydrolysis of the polymer with decimal unit.  means the degree of mineralization and
means the degree of mineralization and  means the concentration of polymer, whose units are mol/L and mg/L, respectively.
means the concentration of polymer, whose units are mol/L and mg/L, respectively.
4. Computation Program Illustration
This section illustrates the computation program by Figure 1.
5. Actual Experimental Tests of Oil Fields
The adaptation efficiency of the software SLCHEM is tested in view of three aspects: dependability, universality and special applicability for large-scale oilfields. The numerical results are dependable by comparing with the actual results and popular business software computations. The software is applied successfully in different fields of Shengli Oilfield and the universality is tested. The software is used in large-scale oilfields and the special applicability is tested.
1) Experiments of the polymer flooding in small-scale oilfields
The rectangle computational domain (Tuo Block 28) is partitioned into 22 × 24 × 6 subdomains with uni-
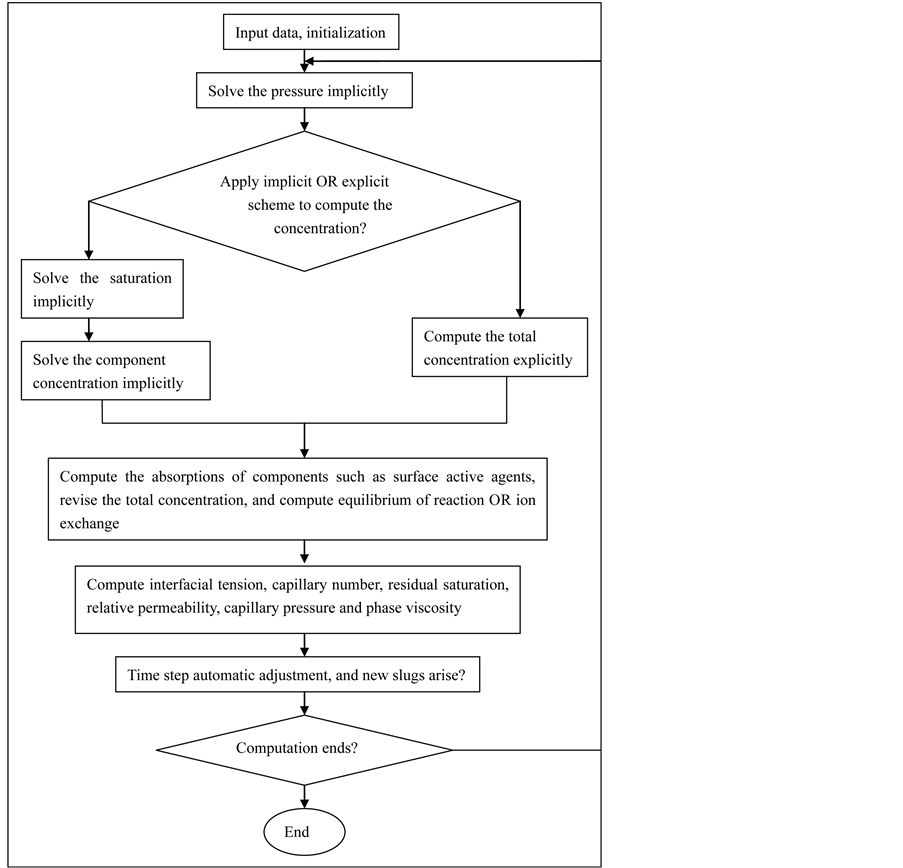
Figure 1. Computation program illustration.
form steps and the spacial steps in x-direction and y-direction are taken as 45.61 m and 47.35 m, respectively. The irreducible water saturation is 0.175, residual oil saturation is 0.25, and formation reserve is 9.9843 × 107 m3. There are fifty four wells in this block. The simulation works about 22,402 days and is considered in three periods. It works in November, 1966 and water is injected in March, 1967. The polymer, whose concentration is 1500 ppm, is injected from June, 2008 to April, 2015. Water is injected again from April, 2015 to January, 2030. The simulation results are illustrated in Table 1.
The comparison of moisture content of produced oil of SLCHEM, VIP, and actual results are shown in Figure 2.
The time cost of SLCHEM is about 0.44 hour, and the material balance error is satisfactory. The relative total error comparison with actual moisture content is about 7.8% before the polymer flooding is injected. All the results show that the computation of SLCHEM runs fast, the numerical results are reliable and this scheme can be applied into present oilfields production.
2) Experiments of surfactant-polymer flooding agents in middle-scale oilfields
The rectangle computational domain (Sheng Block 2) is partitioned into 82 × 74 × 7 subdomains with uniform steps and the spacial steps in 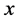 -direction and
-direction and 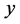 -direction are taken as 33.60 m and 29.29 m, respectively. Formation reserve is 3.4938 × 108 m3. There are sixty three wells in this block. The simulation works about
-direction are taken as 33.60 m and 29.29 m, respectively. Formation reserve is 3.4938 × 108 m3. There are sixty three wells in this block. The simulation works about

Table 1. Numerical results of polymer flooding in small-scale oilfield.
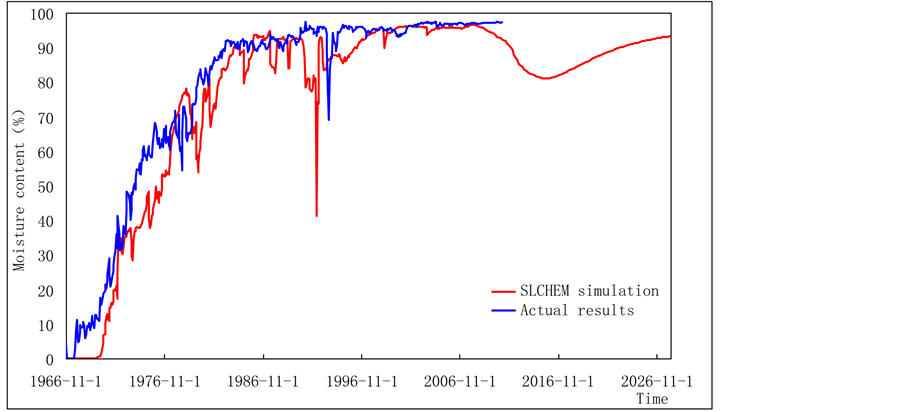
Figure 2. Curve of moisture content simulation of produced oil of polymer flooding in small- scale oilfields.
$2362 days and is considered in three periods. It works on April 1, 1966 and water is injected on January 1, 1974. The polymer, whose concentration is 1600 ppm, is injected from August, 2010 to September, 2016. Surfactant, whose concentration is 0.4%, is injected from August, 2011 to October, 2011. The largest time step is less than five days and the simulation results are illustrated in Table 2.
The comparison of moisture content of produced oil of SLCHEM, ECLIPSE, and actual results are shown in Figure 3. The time cost of SLCHEM is about 4.2 hours, and the material balance error is satisfactory. The relative total error comparison with actual moisture content is about 7.10%. All the results show that the computation of SLCHEM runs fast, the numerical results are reliable and this scheme can be applied into present oilfields production.
3) Experiments of large-scale oilfields
The rectangle computational domain (Gudaoguan Block 3) is partitioned into 72 × 62 × 26 subdomains with uniform steps and the spacial steps in  -direction and
-direction and  -direction are taken as 25 m. Formation reserve is 22,708,200.0 m3. There are one hundred and ninety one wells in this block. The simulation works about 12,965 days and is considered in three periods. It works on September 1, 1971 and water is injected on September 1, 1974. The polymer, whose concentration is 1000 ppm, is injected from March 1, 1994 to November 30, 2003. Water is injected again from December 1, 2003 to March 1, 2007. The largest time step is less than ten days and the simulation results are illustrated in Table 3.
-direction are taken as 25 m. Formation reserve is 22,708,200.0 m3. There are one hundred and ninety one wells in this block. The simulation works about 12,965 days and is considered in three periods. It works on September 1, 1971 and water is injected on September 1, 1974. The polymer, whose concentration is 1000 ppm, is injected from March 1, 1994 to November 30, 2003. Water is injected again from December 1, 2003 to March 1, 2007. The largest time step is less than ten days and the simulation results are illustrated in Table 3.
The comparison of moisture content of produced oil of SLCHEM and actual results are shown in Figure 4.
The time cost of SLCHEM is about 8.45 hours, and the material balance error is 10−6. The relative total error comparison with actual moisture content is about 7.0%. All the results show that the computation of SLCHEM runs fast, the numerical results are reliable and this scheme can be applied into present oilfields production.
4) Numerical simulation of surfactant polymer flooding
The polymer, whose concentration is 1000 ppm, is injected from March 1, 1994 to November 30, 2003. Surfactant, whose concentration is 0.5%, is injected from May 1, 1996 to December 1, 2003. Then water is injected again from December 1, 2003 to March 1, 2007. The largest time step is less than ten days and the simulation results are illustrated in Table 4.
Numerical results of SLCHEM of water flooding, polymer flooding and surfactant-polymer flooding are compared in Figure 5. The time cost of SLCHEM is about 13.5 hours, and the material balance error is satis-

Table 2. Numerical results of surfactant-polymer combination flooding in middle-scale oilfields.

Table 3. Numerical results of polymer flooding in large-scale oilfields.

Table 4. Numerical results of surfactant-polymer flooding.

Figure 3. Curve of moisture content simulation of produced oil of two components combination flooding in middle-scale oilfields.
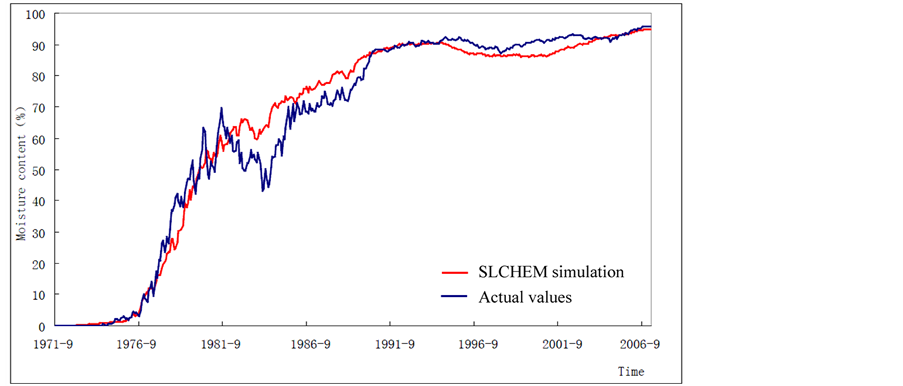
Figure 4. Curve of moisture content simulation of produced oil in large-scale oilfields.
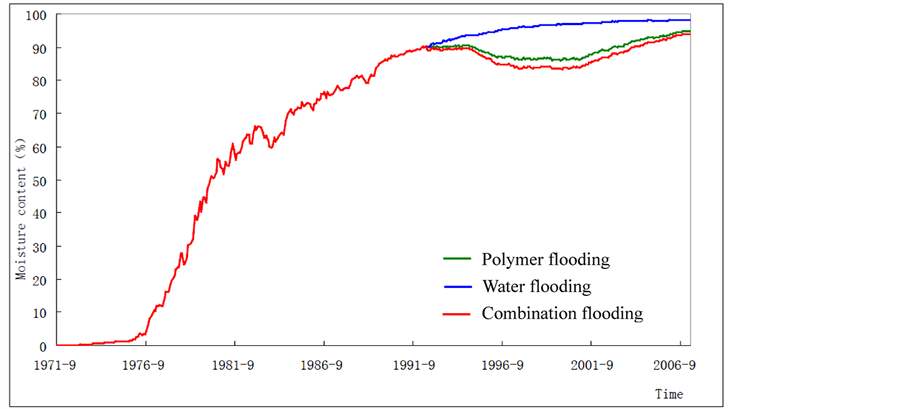
Figure 5. Curve of moisture content simulation of produced oil of surface active agent and combination flooding.
factory. The software has three flooding functions and physical-chemical parameters can be processed effectively. The software simulates reliably and generally based on the above experiments of different scales oilfields and the simulation scale is up to hundreds of thousands nodes.
6. Numerical Analysis of the Model Problem
In this section theoretical analysis is discussed for the numerical simulation of the polymer of porous media. For simplification and without loss of generality, a simple model is analyzed here, a three-dimensional multi-components compressible displacement [1] [2] [12] - [16] . It is a nonlinear system coupled with partial differential equations with initial values and boundary values described as follows
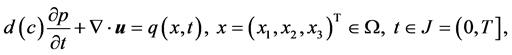 (29a)
(29a)
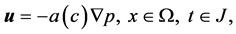 (29b)
(29b)
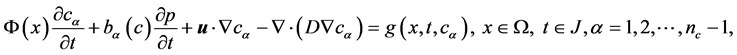 (30)
(30)
where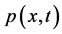 is the pressure of the mixture,
is the pressure of the mixture, 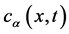 is the concentration of the
is the concentration of the 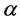 -th component
-th component 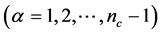 and
and 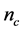 is the number of components. Because of
is the number of components. Because of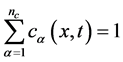 , the only
, the only 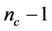 components are independent. Let
components are independent. Let  be a vector function of component saturation,
be a vector function of component saturation, 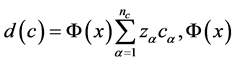 be the porosity,
be the porosity, 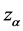 represent a compressible constant of
represent a compressible constant of 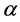 -th component,
-th component, 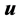 be the Darcy velocity.
be the Darcy velocity.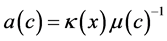 , where
, where 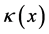 is the permeability,
is the permeability, 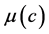 is the fluid viscosity, and
is the fluid viscosity, and ,
, 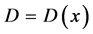 is the convection coefficient. The pressure
is the convection coefficient. The pressure 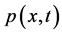 and the vector function of saturations
and the vector function of saturations 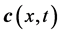 are to be computed later.
are to be computed later.
Impermeable boundary value conditions:
 (31)
(31)
where 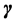 is the outer normal vector of the boundary
is the outer normal vector of the boundary 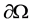 of
of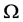 . Initial value conditions:
. Initial value conditions:
 (32)
(32)
For convenience, the computational domain is taken as 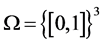 and the problem is supposed to be
and the problem is supposed to be 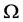 -peri odic, and the impermeable boundary value conditions are dropped. Let
-peri odic, and the impermeable boundary value conditions are dropped. Let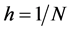 ,
, 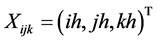 ,
, 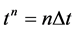 and
and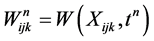 , and take
, and take
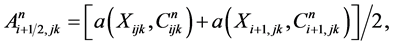 (33a)
(33a)
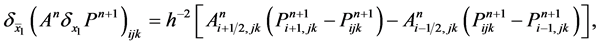 (33b)
(33b)
Then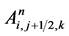 ,
, 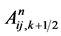 and other notations can be defined similarly.
and other notations can be defined similarly.
An implicit fractional finite difference algorithm for the diffusion Equation (29),
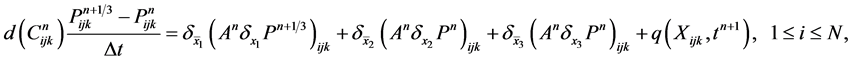 (34a)
(34a)
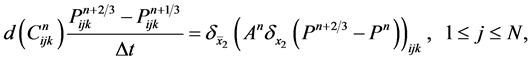 (34b)
(34b)
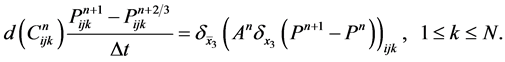 (34c)
(34c)
Compute the Darcy velocity 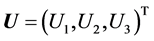 as follows,
as follows,
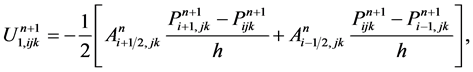 (35)
(35)
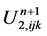 ,
, 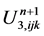 can be obtained analogously.
can be obtained analogously.
An implicit fractional upwind difference method for the saturation Equation (30)
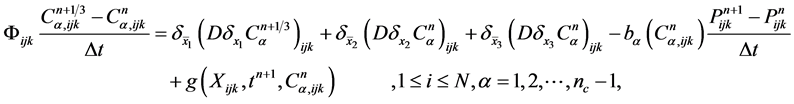 (36a)
(36a)
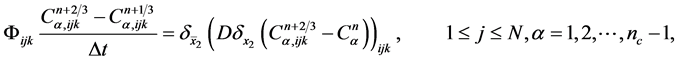 (36b)
(36b)
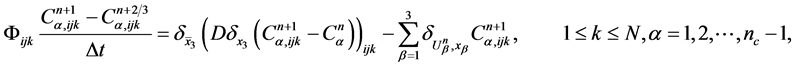 (36c)
(36c)
where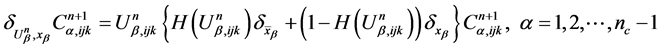 .
. 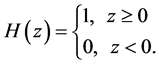
Initial value conditions:
 (37)
(37)
The program of implicit upwind fractional difference method runs as follows. Given 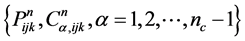 , the values
, the values 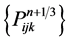 of transition layer is computed by using speedup method in
of transition layer is computed by using speedup method in 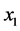 -direction by (34a),
-direction by (34a), 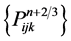 is obtained by (34b), and the solution of pressure
is obtained by (34b), and the solution of pressure 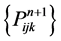 is solved by (34c). The values of Darcy velocity
is solved by (34c). The values of Darcy velocity 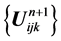 are computed by (35). Secondly, the values
are computed by (35). Secondly, the values 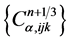 of transition layer is computed by using speedup method in x1-direction by (36a),
of transition layer is computed by using speedup method in x1-direction by (36a),  is obtained by (36b), and the solution of concentration
is obtained by (36b), and the solution of concentration 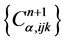 is solved by (36c). Note that the problem is positive definite, the solution of (34)-(36) exists and is sole.
is solved by (36c). Note that the problem is positive definite, the solution of (34)-(36) exists and is sole.
For the model (29)-(32), applying variation technique, energy analysis, decomposition of high order difference operators and theory and technique of product communitivity we can get error estimates in 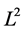 of the implicit fractional upwind difference method stated in the following theorem. The computational algorithms discussed in this paper is based on the mathematical and mechanical considerations.
of the implicit fractional upwind difference method stated in the following theorem. The computational algorithms discussed in this paper is based on the mathematical and mechanical considerations.
Theorem Suppose that the exact solutions of (29)-(32) are sufficiently smooth, and discrete solutions are computed by an implicit fractional step upwind difference algorithm (34)-(36). It holds
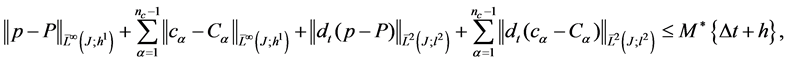 (38)
(38)
where the constant 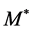 is dependent on
is dependent on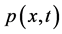 ,
, 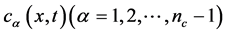 and their derivatives.
and their derivatives.
7. Conclusion and Discussion
Theory, method and application of numerical simulation of high temperature, high salt, complicated geology and large scale oilfields and complicated chemical flooding of flow mechanics in porous media are discussed in this paper consisting of several sections. Summary is stated about our project in Section 1. Mathematical model of permeation fluid mechanics is presented in view of petroleum geology, geochemistry, and computational permeation fluid mechanics Section 2. An implicit refined fractional step combined with upwind difference numerical algorithm based on upstream sequence, is structured in Section 3. A type of software applicable in major industries has been accomplished, mostly carried out the spacial step of ten meters, ten thousands of nodes and tens of years simulation period in Section 4. Some experimental tests taking place successfully in major oil fields such as Shengli Oilfield, are illustrated in Section 5. Numerical analysis proceeds for the model problem and precise theoretical results are stated on mathematical and mechanical consideration in Section 6.
Acknowledgements
The authors express their deep appreciation to prof. J. Douglas Jr, prof. R. E. Ewing and prof. Jiang Lishang for their many helpful suggestions in the serial of research of chemical production. This work is supported by National climbing plan (Grant No. 1990328), National Tackling Key Project (Grant No. 20050200069), Natural Science Foundation of China (Grant Nos. 11101244, 11271231, 10771124, 10372052), National Doctoral Foundation (Grant No. 20030422047) and Natural Science Foundation of Shandong Province (Grant Nos. ZR2011AM015, ZR2009AQ012), National Major Programs for Science and Technology Development (2011ZX05011-004, 2011ZX05052).