The Prime Sequence: Demonstrably Highly Organized While Also Opaque and Incomputable—With Remarks on Riemann’s Hypothesis, Partition, Goldbach’s Conjecture, Euclid on Primes, Euclid’s Fifth Postulate, Wilson’s Theorem along with Lagrange’s Proof of It and Pascal’s Triangle, and Rational Human Intelligence ()
1. Preamble
1.1. Statement of Purpose: Two Complementary Aims
The main design of the present paper is to determine the true nature of the sequence of the prime numbers, or primes, that is, of the sequence 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, and so on.
The sequence of the primes is something of a Holy Grail of number theory, if not of all of mathematics. Hardly any topic has more fascinated professional mathematicians—and also quite a few amateur mathematicians—from time immemorial.
A key question has always been: Is there a single organizational principle that accounts for why any prime follows another prime as next largest prime in the prime sequence? For example, can it be accounted for, by a single principle, at the same time why 13 is next after 11 and why 29 is next after 23?
A correlate question is as follows: Why is 2 the quantity by which 11 is smaller than the next largest prime 13 but 6 the quantity by which 23 is smaller than the next largest prime 29?
It has always been clear to all involved that no one has ever been able to answer these questions.
Of course, nothing is easier to understand on the basis of multiplication tables than that 13 is next after 11 and that 29 is next after 23. This is a form of organization. But it is a form of negative organization. The primes are defined by what they are not. They are what is left after all the numbers that have factors greater than 1 have been eliminated. This process of elimination is also known as the Sieve of Eratosthenes.
By contrast, the key questions formulated above evidently rather concern the positive organization of the prime sequence. In the search for a form of positive organization, it is necessary to leave the numbers that have factors, or the non-primes, out of consideration and focus just on the primes and on how they relate to one another.
Naturally, the relationship between the primes is defined by the quantities that separate them. The quantities in question relating to the part of the prime sequence mentioned at the outset is 1, 2, 2, 4, 2, 4, 2, 4, and 6. This sequence and its continuation has been called the music of the primes.
But no matter how much effort has been expended, it has not been possible to establish why these quantities follow one another in the way that they do. The much-desired Holy Grail is a single principle—a formula—that explains at the same time, say, 1), why 2 is separated from 3 by 1, and 2), why 29 is separated from 23 by 6.
The desired principle would presumably also explain cumulative distances, as in the question: Why is 29 separated from 11 by 18?
Much of the interest in the primes has been to find ever higher ones. But it should not be forgotten that a true overarching principle governing the entire prime sequence ought to explain already why 3 is next after 2 and 5 is next after 3.
It has been deeply felt by many over the decades and the centuries that the discovery of such an overarching principle would reveal something fundamental about the nature of physical reality. In that view, the music of the primes would say something about the music of nature itself.
A first principal aim of the present paper is to show that such overarching principles governing the entire prime sequence do undeniably exist.
The principal demonstration will be cast in Euclidean style. The demonstration will show that the organizational principles in question account for how each single prime relates to every other prime. According to these principles, each prime is like a musical note that makes its own exact contribution to a perfect harmony, the harmony of the primes. The primes behave in an extremely organized manner. They are all attuned to one another in order to achieve a common final and external goal.
At the same time, a second principal aim of the present paper is to show that the principles according to which the prime sequence is evidently organized are for obvious reasons beyond human comprehension.
In sum, the prime sequence is at the same time, 1), highly organized and, 2), fully opaque.
I have not found the view described above represented anywhere in what has been written about the primes.
Instead, the view held widely by default or by implication seems to be that, 1), the prime sequence is by all appearance random but, 2), will potentially at some future time be made transparent.
Because the nature of the organization of the primes is beyond comprehension, it is not possible to compute— according to a single formula or principle—at the same time what the next largest prime after 7 is and what the next largest prime after 11 is. In other words, the prime sequence is incomputable. The numbers 7, 11, and 13 do form part of an organized sequence. But the nature of this organization is incomprehensible to human intelligence.
Is the organization of the prime sequence an axiom? There are axiomatic facets to the organization of the prime sequence. But in the end, there is more to the organization of the prime sequence than an axiom,
One thing seems clear. The identity of the primes is axiomatic. An axiom is an observation that is so abundantly obvious that no one sees a need for proof. One simply accepts the observation without proof. For example, it is obvious to all that 7 and 11 are primes. There is no need to prove that they are. Everyone accepts without proof that they are primes.
But what in the case of a higher prime such as 99,923? It is not immediately clear whether this is a prime or not. Does this make the identity of the primes less than abundantly obvious and therefore less of an axiom? It does not. The reason is as follows.
On what grounds does one come to accept that 7 and 11 are primes? One does this more or less empirically by testing whether any number lower than half or so of 7 or half or so of 11 is a factor of 7 or 11.
The matter is fully obvious. The very same test can be applied to 99,923. If no factors can be found, then 99,923 can simply be identified as a prime without proof.
The difference between 7 and 11, on the one hand, and 99,923, on the other hand, is that it takes much longer to apply the procedure in question to 99,923 than to 7 or 11. But the fact that the procedure lasts much longer in the case of 99,923 does not make it any less obvious that 99,923 is a prime than that 7 and 11 are primes. It is not because it is more onerous to establish that 99,923 is a prime that it is axiomatically less obvious that 99,923 is a prime.
In fact, one might speculate that, if the human brain were much, much larger while exhibiting the same structure, it might be as easy to establish that 99,923 is a prime as that 7 and 11 are.
The identity of the primes is axiomatic in the sense that one accepts it without proof. An axiom is something that is completely self-evident all by itself, like 1 + 1 = 2. One does not expect anything more.
The prime sequence is different. It will be shown below that it is highly organized. The fact of this organization seems so obvious that it may be deemed axiomatic. But it will also be shown that the organization in question transcends human cognition. This fact too seems so obvious that it may be deemed axiomatic. But all this does not quite yet make the prime sequence itself axiomatic.
The difference between the organization of the prime sequence strictly speaking and an axiom is as follows. From the fact that the organization of the prime sequence transcends human cognition, it follows that there is something more about the prime sequence than just an axiom. However, the limits of rational human intelligence prevent one from reaching that something more. By contrast, with axioms strictly speaking, there is nothing more. Axioms constitute an endpoint. The prime sequence points to something beyond.
It can be concluded from the incomputability of the prime sequence that certain facets of physical reality are beyond human comprehension. But that is in a sense not entirely unexpected. There is probably no one who doubts that the understanding of the universe by the human intellect in its current state is subject to certain absolute limitations. It appears that the organization of the prime sequence involves one of those absolute limitations.
In sum, considering the current circumstances of the human condition, it is time to give up hope of explaining why the prime sequence is the way it is.
If someone publishes a formula to the contrary hundreds of pages long that only two and a half mathematicians can understand or claim to understand, I might have questions. Also, approximate results, however close, in the form of certain series or the like, are not the same as exact results.
The great L. Euler (1707-1783) already had deep suspicions about the possibility of providing answers to the questions posed at the outset of this section and he presumably suspected that the prime sequence is random. The great F. K. Gauss (1777-1855), who considered number theory—to which the study of primes belongs—the prince(ss) of mathematics, lent the matter his close attention from a very young age. But he, like L. Euler, never got anywhere even close to mere hints of answers to the questions posed above.
It is true that F. K. Gauss and many in his wake have obtained significant—though only approximate—results in regard to the question as to how many primes there are up to a certain number, answering questions like the following: How many primes are there up to the number 1000? The number in question is now written as π (1000); in this case, π is not the ratio between a circle and its diameter. The desired number is 168.
According to one approximate function proposed by mathematicians, namely , the number is 145; according to a second, F. K. Gauss’s so-called Li-function, it is 178; and according to yet a third,
, the number is 145; according to a second, F. K. Gauss’s so-called Li-function, it is 178; and according to yet a third, 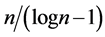 , it is 169. Although the third function is closest to the actual number in this case, it may not be in other cases.
, it is 169. Although the third function is closest to the actual number in this case, it may not be in other cases.
But these results, significant though they are, seem like light-years removed from explaining the prime sequence itself. The well-known Riemann Hypothesis also pertains to the general question of how many primes there are up to a given number. This hypothesis has been tested so often—without any failure—for ever higher numbers that mathematicians now more or less generally agree by default that the hypothesis must somehow be true. Then again, all agree that there is still no proof.
As regards the history of mathematical research on primes, L. E. Dickson has described it from its beginnings in antiquity in excruciating detail [1] . As regards general access to the topic, three books of more recent date— addressed to wider audiences—have done much to facilitate access to what some have called the “mystery” of the primes [2] -[4] .
It is true that the primes are something of a mystery, but not in the way that one might suspect. They are considered a mystery, it seems, because they seem random. But in what follows, it is shown that they are not random at all. They appear to be highly organized. But this organization is inaccessible to human comprehension. And rather therein, it might be said, lies the mystery.
1.2. Structure and Contents of the Present Paper
Sections 8 and 9 form the paper’s center. The present Section 1 contains introductory observations.
Section 2 describes how Euclid does number theory in geometrical fashion. The reason for this description is that this manner of doing number theory will play a role in the demonstration of the paper’s main thesis in Sections 8 and 9.
Section 3 describes another key ingredient in the demonstration of the paper’s main thesis in Sections 8 and 9, namely that which will be called here L. Euler’s infinite prime product.
Section 4 provides historical context by describing the Riemann Hypothesis. The reason for the description is that L. Euler’s prime product is nowadays mostly discussed in relation to this hypothesis. The hypothesis is itself not analyzed. Still, a conclusion is proposed regarding its relevance to the prime sequence. It is suggested that, even if the hypothesis is ever proven, which seems unlikely, it will be irrelevant.
The Riemann Hypothesis has by now been tested for so many numbers that it is generally assumed that it is true. But everyone agrees that there is still no proof. There is a general expectation that an understanding of the Riemann Hypothesis may well reveal a deep truth about the prime sequence. However, it is proposed in the present paper that, even if the hypothesis is true, it will not reveal anything about the ultimate nature of the prime sequence.
Section 5 applies Euclid’s geometrical way of doing number theory, which is described in Section 2, to the prime sequence. This manner of viewing the prime sequence will play a role in the demonstration of the main thesis of the paper in Sections 8 and 9.
Section 6 describes four possible approaches to interpreting the prime sequence.
Section 7 describes a fifth approach, the one followed in the present paper.
As was said, Sections 8 and 9 are central to the paper’s structure.
Section 8 shows how the prime sequence is highly organized and not random at all.
Section 9 shows that the organization in question is not accessible to human cognition.
Section 10 is a sort of appendix to Sections 8 and 9. It addresses a potential objection to declaring the prime sequence at the same time highly organized and inaccessible to human cognition.
Section 11 shows certain patterns of organization according to which the primes, the non-primes, the even numbers, and the uneven numbers all relate to one another in what might be called a grand mathematical “poem”. Among the Equations that will play a role in this “poem” are the following:




Remarkably, multiplying the first Equation pertaining to the primes with the fourth Equation pertaining to the uneven numbers yields the same result as multiplying the second Equation pertaining to the non-primes with the third Equation pertaining to the even numbers, as follows:

Section 12 describes how the Equations adduced in Section 11 are obtained.
Section 13 is a sort of appendix to Sections 11 and 12. It describes patterns and Equations related to those described in Sections 11 and 12. For example, one Equation involves an interesting way of defining the number 1, as follows:

The primes and the non-primes jointly but also distinctively converge on 1.
Section 14 examines the question as to how special the prime sequence really is, now that Sections 11, 12, and 13 have revealed patterns according to which the primes are no more special than the non-primes, the even numbers, and the uneven numbers.
Sections 15, 16, 17, 18, and 19 treat topics that are related to the paper’s main topic, the prime sequence.
Section 15 provides context by describing some reflections by Aristotle on the limitations of rational human intelligence. The inaccessibility of the prime sequence to human cognition is such a limitation. It is therefore of interest to probe what others have said about such limitations, in this case Aristotle.
Section 16 presents an obvious way of looking at primes that I have not found applied anywhere. It is shown that the study of the primes can be seen as one manifestation of partition theory. But observing how far partition theory is removed from saying anything about the structure of the prime sequence only supports the general point made in the present paper that the sequence is inaccessible to human cognition.
Section 17 investigates what the paper’s main thesis concerning the prime sequence means for the analysis of Goldbach’s Conjecture.
Section 18 examines Euclid’s approach to the primes and the prime sequence.
Section 19 is a comparison between the analysis of Euclid’s Fifth Postulate and the analysis of the prime sequence. Both involve mathematical problems that have over the centuries resisted countless attempts at deeper understanding. In this sense, they have similar status in mathematics. A comparison may therefore be useful.
Section 20 is an excursus that does not concern the prime sequence directly, but rather primes in general. The subject matter of this section arose in the course of my engagement with primes in general and this is as good a place as any to address it. The specific topic is Wilson’s Theorem, that is, J. Wilson’s theorem, pertaining to the primes, perhaps the most beautiful theorem pertaining to primes, if already merely owing to its eminent simplicity.
It will be useful to contemplate the earliest proof of this theorem, perhaps the most informative ever, namely J.-L. Lagrange’s. It will also become evident in this connection that there is room for a better appreciation of the coming into existence of Wilson’s Theorem in relation to what is widely regarded as the most beautiful proof of any theorem pertaining to primes ever, Euclid’s proof of the proposition that there are an infinite number of primes.
1.3. The Larger Project of Which the Present Analysis of the Prime Sequence Is Part
The present paper is about primes. But the ulterior goal of the line of argument presented in this paper goes beyond primes. The paper is part of a larger project that aims to produce a complete and final theory of rational human intelligence. In that regard, the primes are considered interesting for what they reveal about the nature of rational human intelligence and its place in the universe.
What exactly does it mean for rational human intelligence to come face to face with the prime sequence? What exactly does it mean, more generally, for rational human intelligence to come face to face with a curtain behind which it cannot look, face to face with a veil that it cannot lift?
The brain is a physical tool with absolute material limits. Most everyone will probably agree that there are things that it can do and things that it cannot do. Absolute material limits mean that there is an end to what it can do and also raise the specter of describing all of it because, after all, it ends somewhere. But where exactly does it end? What is the line between what the brain can do and what it cannot do? Where precisely is the curtain? Primes provide one means of probing those absolute limits.
The first installment of the afore-mentioned theory has now appeared [5] .
This first installment deals with, as its title states, the mathematical foundations of the theory. Little or nothing is known at this time about how rational human intelligence propagates electrochemically in the brain. And yet, it is proposed that a complete and final mathematical and physical theory of rational human intelligence is now possible. There is every reason to expect that the biochemistry of the brain will be completely revealed at some future time. The brain is after all a finite material structure. Then again, it is also anticipated that, even when the brain’s physical makeup is completely laid bare, the theory of rational human intelligence will still in essence be a mathematical and physical theory.
The theory of purely rational human intelligence is in the end not about biology, chemistry, culture, electricity, logic, mysticism, neuroscience, philosophy, psychology, religion, sociology, or theology. It is entirely about the purely mathematical description of a physical event. That is why it has been deemed necessary to present the theory in a journal of mathematics, even though the author is not strictly speaking a mathematician. In fact, there seems to be no way that the theory of rational human intelligence cannot be mathematical. However, the theory is not quantitative-mathematical—that is, not mathematical in the way most everyone would define mathematical—but rather digital-mathematical.
Emotional intelligence is another matter. Substances such as adrenaline, dopamine, and serotonin probably have a lot to do with it. Emotional intelligence is presumably analogue, not digital. One can be a little happy and a little more happy, and so on. The same with angry. It is not just On or Off. Furthermore, the correct results of rational human intelligence are mathematical and ought to be the same for everyone. By contrast, what makes one person happy can make another person angry. Then again, quite a few things make everyone happy or everyone angry.
The digitality of rational human intelligence consists entirely of four flavors, as follows: 1), Selection Digitality (SelDi); 2), Nexus Digitality (NexDi); 3), Certification Digitality (CerDi); and 4), Supplement Digitality (SupDi).
The first two flavors, SelDi and NexDi, are described for the greater part—though not entirely—by G. Boole.
The essence and the fundamental digitality of the other two flavors, CerDi and SupDi, have already been defined and outlined in earlier work by the present writer [6] [7] .
CerDi and SupDi pertain more to the specifically human component of rational human intelligence. That may be why these two flavors were not detected by mathematicians like G. Boole and J. Venn. Yet, Certification Digitality is in a sense the cornerstone of rational human intelligence in as far as the humanity of rational human intelligence is concerned. Even if it may not be part of the digital mathematics that drives logical reasoning, CerDi does allow the brain to draw inferences that lead it to act.
The second installment of the theory of rational human intelligence will be concerned with Selection Digitality (SelDi). Probability theory will play a crucial and dominant role in the exposition of SelDi.
Incipient work on installment two soon revealed that the concept of partition is an essential component of probability theory. And it is the contemplation of partition that led to the consideration of primes. In fact, the primes can be viewed as a special problem of partition theory. A prime number of things cannot be divided into a certain number of equally large groups. In fact, what is said about primes could allow certain conclusions about partition theory. A suspension of work on installment two became desirable in order to establish what the primes are all about. This led to the present paper. Some of the present paper’s contents is briefly anticipated in two sequences that I have published in the Online Encyclopedia of Integer Sequences as A231273 and A231327 [8] .
2. Back to Euclid: Viewing Numbers Geometrically
Over the centuries, much rule-determined behavior to which primes are subject has been uncovered. But when it comes to the prime sequence, nothing is more common than to read that it is—or seems to be—completely random. There appears to be no rhyme or reason to a sequence such as 7, 11, 13, 17, 19, 23, 29, 31, 37, and so on.
Using metaphorical language, it can be said—and has been—that the primes do not sing [9] .
The design of what follows is to show that the primes do sing. However, again using a metaphor, it can be said that their clearly discernable melodies follow the beat of a different drum, and a drum that is inaudible to human ears.
In assessing the prime sequence and determining how they are organized, it will be useful to visualize numbers just as Euclid does in the three books of his celebrated Elements that deal with number theory, namely Books 7, 8, and 9. Book 10 treats related material. More than two thousand years of mathematical research have amply demonstrated that it has so far always been wrong to bet against Euclid.
Numbers denote quantities. There can be no doubt that Euclid visualized these quantities in geometrical terms as lines. For example, if the number 2 is a line, then the number 6 is a line that is three times as long.
In modern mathematics, it is common to say that 2 is a factor of 6 or also that 2 is a divisor of 6. Euclid’s conception of the relation between 2 and 6 is quite different. In other words, if one takes a line of size 2, it can be fitted a number of times inside a line of size 6, or 2 + 2 + 2 = 6.
According to Euclid, a number that is the divisor or factor of another number is conceived of as a line that “measures” (Greek katametrein) another line. A line that “measures” another line is a line that fits exactly a certain number of times into another line.
Nowhere in his treatment of number theory does Euclid use numbers as we understand and notate them, namely as “1”, “2”, “3”, and so on. Instead, he refers to numbers as lines, for example as AB and CD.
Euclid is therefore not concerned with quantities per se. Nowhere does he state how long lines are. The exact lengths of the lines themselves as representations of numbers are irrelevant. In other words, line symbols such as AB and CD do signify numbers. But they do not stand for numbers such as 1, 2, or 3, and so on. Euclid’s focus is on the relations between lines of different length.
One example of such a relation is found in Proposition 5 of Book VII. Euclid’s formulation, augmented by slight clarifications, is as follows:
If a first number be a part of a second number, and a third number be the same part of a fourth number, then the sum of the first number and the third number will also be the same part of the sum of the second number and the fourth number.
From the proof, it is clear that Euclid imagines this as follows: If a line AB measures a line CD in a certain way in the sense that AB fits a certain number of times into CD and if a line EF measures a line GH in that same way in the sense that EF fits that same number of times into GH, then the total length of AB and CD together will also fit exactly that very same number of times into the total length of EF and GH together.
For example, in modern terms, if 5 goes 4 times into 20 and 6 goes likewise 4 times into 24, then 11 or 5 + 6 will go likewise 4 times into 44 or 20 + 24.
Since early modern times, the following algebraic representation is the rule. If

then
 .
.
Adding up both sides of the two Equations readily leads to this result. Again, using integers, if

and
 ,
,
then
 .
.
Euclid’s books on numbers are therefore in great part about what is now called algebra, that is, about general relations between numbers. But they do move into number theory whenever he examines relations between types of numbers such as prime numbers and non-prime or composite numbers.
That Euclid visualizes numbers in geometric fashion is also immediately apparent from the fact that he describes a square number, say 22, as a plane and a cube number, say 23, as a solid.
Thus, Definition 16 at the beginning of Book 7 of his Elements is as follows [10] :
[W]hen two numbers having multiplied one another make some number, the number so produced is called a plane, and its sides are the numbers which have multiplied one another.
Clearly, the “sides” of a “plane” are lines. In fact, Definition 6 of Book 1 of his Elements is as follows [11] :
The extremity of a surface are lines.
And a “plane” (Greek epiphaneia) is nothing but a type of “surface” (Greek epipedos). In fact, in Definition 7 of Book 1, the following is stated [11] :
A plane surface is a surface which lies evenly with the straight lines on itself.
Just as Euclid describes two numbers multiplied with one another as a “plane” in Definition 16 of Book 7, he calls three numbers multiplied with one another a “solid” in Definition 17 of Book 7.
The aim of the present line of argument is to visualize the prime sequence—and more specifically the gaps between any prime and the next largest prime or between any two primes for that matter—in geometrical and Euclidean fashion according to a single organizational principle that is external to the primes. But first, it is necessary to introduce a concept that will play a crucial in this process of visualization.
3. L. Euler’s Infinite Prime Product Equation
The following infinite sum is known as the harmonic series:
 (1)
(1)
It is known that it diverges. That is, it gets ever larger and larger and moves ever closer to infinity. Thus, the following Equation applies:

N. D’Oresme already proved this in the Middle Ages [12] .
Expression (1) is evidently the same as
 .
.
And it is also—to satisfy a certain sense of consistency—the same as:
 .
.
In other words, the shared exponent of the numerators is 1.
But what about when the exponent is 2, as follows?
 . (2)
. (2)
It is easy to establish that the infinite series in (2) does not diverge. But on which number does it converge? J. Bernoulli—that is, Jakob (1654-1705)—first asked the question, at least in the written record, and it was L. Eu-
ler who first proved in 1735 that (2) converges on , that is, on about 1.644934 (I round off at a zero) [13] .
, that is, on about 1.644934 (I round off at a zero) [13] .
Accordingly,
 . (3)
. (3)
It is not necessary to look up L. Euler’s celebrated proof in a book. These days, one can find video descriptions of it on the Internet.
In a different connection, L. Euler obtained another remarkable result, the following:

And more generally, the following:
 (4)
(4)
In (4), expression (2) is equated with an infinite product that involves all the, and only the, primes. J. Derbyshire gives a convenient description of L. Euler’s proof, that is, of how L. Euler converts the infinite sum of expression (2) into an infinite product involving all the primes [14] . L. Euler’s original is written in Latin.
Equation (4) is known by more than one name. I will call it L. Euler’s infinite prime product Equation. The product involves all the primes, hence prime product. The product is infinite, hence infinite prime product. Naming the Equation after the product, and not the sum, is inspired by the fact that the product is derived from the sum and not the other way around. The product by itself may be called L. Euler’s infinite prime product.
It evidently follows from Equations (3) and (4) that
 (5)
(5)
Perhaps, some may prefer to write this Equation as follows:
 (6)
(6)
Equation (6) is analytically more satisfying. It conveniently signifies that, on the left side of the Equation, the numerators have to be of the same number as the denominators if the infinite product is to keep converging on the result on the right.
In Equation (5), the primes are organized in a certain way to converge on a specific number. As regards the nature of this organization, a suggestive variant of (5) is as follows:
 (7)
(7)
Equation (7) can also be written as follows:

The infinite product in Equation (7) exhibits the following remarkable property. The terms are all ratios either of a prime number to a composite number that is one larger or of a prime number to a composite number that is one smaller.
It may be noted that numbers that are larger or smaller by two than a prime could themselves be primes. But not numbers that are larger or smaller by one, except 2. All the ratios except the first two are therefore all between a prime and a non-prime.
I do not think that anyone has ever attributed any significance to Equation (5) or tried to exploit it for an ulterior design. And yet, I am convinced that it reveals something truly fundamental, not only about the nature of the primes, but also about the nature of rational human intelligence.
As regards expression (2), it is altogether possible to contemplate exponents higher than 2. And it comes as no surprise that that is exactly what L. Euler already did. In other words, the focus turned towards the generalized expression
 (8)
(8)
in which n is a natural number larger than 1.
L. Euler noted a remarkable fact pertaining to (8). When the common exponent of the numerators is even, 2, 4, 6, 8, and so on, a precise solution involving π is possible. But when the exponents are uneven or odd, only an approximate solution is attainable. The variants of (8) that have a precise value involving π can therefore be expressed as follows:

In this infinite sum, all the powers can be viewed as a second power, even if the second power of another power.
How can one account for the connection with π? One is reminded in an uncanny way of another connection of π with the second power.
As a point moves on a circle, the triangle formed by this point and the two extremities of the diameter is at all times a right triangle. The lengths of the two ever changing lines that define the position of the point moving on the circle is therefore at all times defined by the Pythagorean theorem, which is all about the second power.
But what about an exponent other than a natural number? The question is addressed in the next section. The matter is not directly relevant to the main line of argument of the present paper. But still, it does concern one of the best-known hypotheses of mathematics. And, more importantly, the prime sequence is involved.
4. The Riemann Hypothesis
B. Riemann generalized expression (6) to all complex numbers [15] . He represented the complex numbers by the symbol s. And ever since, everyone has done so in this context. Accordingly, expression (6) becomes
 (9)
(9)
B. Riemann contemplated the corresponding function involving continuously changing s. He called it the Zeta Function, after the sixth letter of the Greek alphabet, . And ever since, everyone has done so in this context. Accordingly, expression (9) becomes
. And ever since, everyone has done so in this context. Accordingly, expression (9) becomes

B. Riemann evaluated this function and found values for all numbers except 1. He notes that, for certain values of s, the function  or Zeta Function is 0. Among these values are the negative even numbers. But these are now called “trivial” zeros. In addition, certain complex numbers of the type
or Zeta Function is 0. Among these values are the negative even numbers. But these are now called “trivial” zeros. In addition, certain complex numbers of the type  (also written as
(also written as ) in which a is the real part, also yield 0 as value of the function. These are now called “non-trivial” zeros.
) in which a is the real part, also yield 0 as value of the function. These are now called “non-trivial” zeros.
B. Riemann hypothesized that the real part of the complex numbers in question is always . This is known
. This is known
as the Riemann Hypothesis. Many consider it to be one of the most important unsolved mathematical problems, some even the most important. Most of those knowledgeable in the matter assume that the hypothesis is true. But all agree that no proof has been found.
Owing to the relation between the Riemann Hypothesis and L. Euler’s infinite prime product Equation, it is assumed that a proof of the Riemann Hypothesis might provide crucial insights into the prime sequence.
The Riemann Hypothesis does not play a role in the line of argument presented in this paper, the aim of which is to show that the prime sequence is highly organized while fully opaque.
The opposite is rather the case. The thesis proposed in the present article, if it is correct, in a way implies consequences for the Riemann Hypothesis. Perhaps someone will some day prove the Riemann Hypothesis. But many would seem to doubt that anyone will.
In any event, it is not certain at all that a possible proof would shed light on the true nature of the prime sequence. What is proposed in the present paper rather implies by necessity that it would not.
5. A Geometric Interpretation of the Prime Sequence in Euclidean Fashion
It follows from Equation (5) that
 (10)
(10)
The aim is to visualize Equation (10) in Euclidean fashion.
In general, as was noted above, Euclid imagined numerical quantities as lines of a certain length. Accordingly, Equation (10) can be interpreted as a line that starts at 6.00 and ends at 9.8696∙∙∙. The length of this line is therefore 3.8696∙∙∙.
The function of the expression
 (11)
(11)
in Equation (10) is in a sense to bridge the gap between 6 and π2 or 9.8696∙∙∙. Each single prime contributes to the bridging of the gap.
In other words, in conjunction with denominators that are either one larger or one smaller, the primes as numerators can be seen to behave together as a group in relation to π.
How can the gap between 6 and π2 be described in Euclidean fashion?
It seems clear that, in Euclid’s preferred geometrical visualization, the effect of multiplying 6 by each successive fraction of expression (11) is to traverse a well-defined section of the line interval whose length is 3.8696∙∙∙, starting at 6 and moving to π2 or 9.8696∙∙∙. Each traversed interval can be defined in exact numerical terms.
For example, the first fraction of (11), which involves the smallest prime, namely 2, is as follows:
 .
.
It is evident that
 .
.
Accordingly, by multiplying the left extremity of the line that stretches from 6 to π2 or 9.8696∙∙∙, a distance amounting to 2 has been traversed starting at 6 and ending at 8. In other words, the length of the traversed distance is 2.
What matters presently is that the first prime 2 can be correlated with a precisely defined section of the line stretching from 6 to π2 or 9.8696∙∙∙, the section beginning at 6 and ending at 8.
Likewise, the section that still remains to be traversed is evidently

By the same token, all the other primes all the way to infinity can also be correlated with a precisely defined section of the line stretching from 6 to π2 or 9.8696∙∙∙.
For example, the second largest prime, 3, can be correlated with its own section as follows.
By multiplying 6 by the first fraction involving the first prime in expression (5), the line running from 6 to 8
has been obtained above. The first result 8 can now be multiplied by the second fraction  to obtain a
to obtain a
second result. The second result is as follows:
 .
.
What matters presently is that the second prime 3 can be correlated with a precisely defined section of the line stretching from 6 to π2 or 9.8696∙∙∙, the section beginning at 8 and ending at 9. Its length is 1.
It is also evident that multiplying 6 by both afore-mentioned fractions results in a line section that is the sum of the two line sections pertaining to the two primes 2 and 3, as follows:
 .
.
The line section runs from 6 to 9. What remains is evidently .
.
Following the same procedure, it is possible to correlate each single prime all the way to infinity geometrically and numerically with its own section on the line that is 3.8696∙∙∙ long and runs from 6 to π2 or 9.8696∙∙∙. Furthermore, by combining a given prime with all the primes smaller than itself, each single prime can be associated with an ever dwindling remaining line section up to π2.
What follows are the precise numbers in question up to the sixth largest prime, 13. There is no need for adducing additional primes to make the point.
When the line sections correlated with all the primes all the way to infinity are added up, the entire line running from 6 to π2 will be obtained.
and so on.
The list above could be extended into all perpetuity. Accordingly, the successive results would ever more closely approach π2. And apparently, the total result is equal to π2 in the dimension of infinity.
In any case, the precise numbers do not matter much. Nor do such interesting facts as that 3072 equals 3 × 212.
What matters truly in the present context is that the interpretation of the prime sequence in Euclidean fashion allows the discernment of an extremely high degree of organization in the prime sequence that can be defined in strictly numerical terms. This high degree of organization contradicts the general perception that the prime sequence is entirely random. It is not.
Before describing this type of organization in greater detail in Section 8, it will be useful to determine in which way the present approach to the prime sequence differs from past approaches in the next two sections.
6. Four Past Approaches or Attitudes to the Prime Sequence
The prime sequence has always seemed utterly random to all. To be sure, the primes exhibit a high amount of rule-determined behavior, as established by many centuries of discoveries about them by number theorists. An example is Wilson’s Theorem, that is, J. Wilson’s theorem, first proven by J.-L. Lagrange. The theorem and the proof are both discussed in Section 20 below.
But in spite of all this well-known regularity exhibited by the primes, the prime sequence itself gives every appearance of winding its way through the sequence of the positive integers in obedience to no recognizable pattern whatsoever: 3 follows 2, 5 follows 3, 7 follows 5, 11 follows 7, and so on, in no apparent pattern whatsoever.
It would seem as if four approaches to the prime sequence are conceivable.
The first approach is that one accepts the prime sequence as an axiom. It seems so obvious why 13 follows 11 and 17 follows 13. They are the numbers that are left once one has produced by multiplication all the numbers that are non-primes, as in the Sieve of Eratosthenes. In this approach, all this is by itself considered so obvious that there is no desire for looking further.
The second approach is closely related to the first. The second approach takes into consideration the possibility of a pattern. But the approach involves positively denying that there is a pattern. As in the first approach, there is no desire to look for one.
The third approach is to assume that there is a pattern but that it cannot possibly be detected.
These first three approaches have in common that they imply that one should not give the prime sequence any further thought.
The fourth approach is to assume that there is a pattern but that it has not yet been detected and may perhaps some day be.
The four approaches all have the same effect: no pattern governing the prime sequence can be formulated. Therefore, choosing between the four is rather theoretical in the sense that the practical effect is exactly the same in all four.
It would appear, however, that the minds of many by default probably linger with the fourth approach. One likes to think that everything exists for a reason. Then why not also the prime sequence? And after all, why give up hope? One thing is certain: The search for patterns in the prime sequence has not been called off.
But there is a fifth approach, which is adopted in the present paper. It is in this regard that the present paper departs radically from universally received opinion and from the four approaches defined above. The new approach is described next.
7. A New, Fifth, Approach to the Prime Sequence
The four approaches defined in Section 6 above all have in common that they assume that no pattern can be formulated.
By contrast, the fifth approach to be described next involves demonstrating that there is in fact a pattern and describing the pattern. In fact, there is more than one pattern, in fact an infinite number of them. All these patterns can be defined in numerically precise terms. Together, the patterns evidence that the prime sequence is extremely highly organized. It is not random. In other words, the fact that 3 follows 2, 5 follows 3, 7 follows 5, 11 follows 7, and so on, is not random.
But the fifth approach involves something else. A distinction is necessary between the patterns as facts and the true nature of the patterns. It can be shown that, for a fact, there are patterns. However, it is also immediately obvious that the true nature of these patterns is opaque. The true nature transcends rational human intelligence.
This means that it is not possible to compute by means of one single principle or formula why 5 follows 3 and 19 follows 17. The prime sequence is not computable by the human brain.
8. Highly Organized Patterns Exhibited by the Prime Sequence
G. H. Hardy and E. M. Wright state that “the distribution of the primes in detail is extremely irregular” [16] . I do take issue with this statement.
In Section 5, the prime sequence was related to π2. It was noted that

It was also noted that this Equation equals

But what does this Equation mean? It seems to have remained unappreciated that the Equation reveals that the primes are organized to an extremely high degree according to a single overarching principle.
In regard to this principle, each prime relates in a precise manner to every single other prime, to any single set of other primes, and to all other primes together in an empirically definable and numerically precise manner. In short, there is not a single conceivable relation among the primes viewed individually, or as sets, or all taken together, that is devoid of organization according to this single overarching principle.
What is this high degree of organization? It is evident from what has been said in Section 5 that each prime can be associated in Euclidean fashion with an accurately definable section of a line that extends from 6 to π2 or about 9.8696∙∙∙ and is about 3.8696 long.
How large exactly is this line section? Let us take, for example, the line section associated with the prime 5.
In Section 5.1, the length of the line section was determined to be exactly  of the expanse from 6 to π2, which
of the expanse from 6 to π2, which
amounts to about 3.8696.
How was , as the precise magnitude of the line section pertaining to the prime 5, obtained? It was obtained
, as the precise magnitude of the line section pertaining to the prime 5, obtained? It was obtained
as an addition to the distance away from 6, a distance that is itself obtained by all the primes that precede 5, that is, in this case 2 and 3.
Each line section is a component of a product that encompasses all the primes. Evidently, every component of a product contributes to the total quantity of a product. Consider a product such as
 .
.
The result is 720. Changing any of the six components affects the final result. In other words, every component needs to be exactly as large as it is and behave exactly in the way in which it does for the final result to be obtained. What is more, because all the components are multiplied with one another, each component relates to every other component or any group of two or more components.
Multiplication has been represented as addition of line sections in Euclidean and geometrical fashion to visualize the organization of the prime sequence better. This geometrical representation is not indispensable. The arithmetic progression of the infinite product also reveals the organization of all the primes working as a team, as it were, to yield a common end result.
For example, one might elect to focus on the ratio of every prime to every preceding prime. In fact, Euclid also pays much attention to proportions.
Thus, the ratios of Equation (6), namely

can be written as follows:
 .
.
These ratios have a common goal. Each is exactly as large as it is, no smaller, no bigger, in order to achieve the result to the right.
In this regard, the degree of organization of the primes could not be higher. This extremely high degree of organization defines the following relations, and many more:
1) the relations between each prime, or group of primes, and each other prime, or other group of primes, or all other primes together;
2) the relations between each prime, or group of primes, or all primes, and π, in this case more specifically π2.
3) the relations involving other patterns of successive line sections obtained by changing the order of multiplication, for example as in
 ;
;
4) the relations involving yet other patterns of successive line sections obtained by related Equations such as
 (12)
(12)
and so on.
The results in 4) are derived from the values that the Zeta Function yields for the even numbers higher than 2, that is, 4, 6, 8, 10, and so on. The values can be conveniently accessed on the web at Wolfram Research [17] . Thus,
 (13)
(13)
and so on.
According to Equation (4),
 (14)
(14)
and so on.
The Equations in (13) together with the Equations in (14) yield the Equations in (12) above.
The second Equation in (12) can also be written as follows:

The generic form is as follows:
 ,
,
in which x and y are natural numbers; x is 1 for the exponents 2, 4, 6, 8, and 10.
The fraction  above tends to 1 as the exponent n increases towards infinity. Part of the progression is as
above tends to 1 as the exponent n increases towards infinity. Part of the progression is as
follows (I round off at the first zero):
exponent 6: 1.017343 ;
;
exponent 8: 1.004 ;
;
exponent 10: 1.000994575127818 ;
;
exponent 12: 1.000246 ;
;
exponent 14: 1.000061248135 ;
;
exponent 16: 1.0000152822594 ;
;
and so on.
This convergence is obvious from the following Equation, a variant of Equation (4):

Evidently, as n increases, there is less that gets added to 1 in the infinite sum, and multiplying the fractions of the infinite product gradually approaches 1.
The dimension of infinity is a challenge to the mathematical imagination. Consider the following Equation:

One is invited to imagine that, the more terms one adds starting from the first term to the left, namely 1, the smaller the difference of the sum with 2 becomes and that, if one goes on into infinity, the difference will become 0. L. Euler also makes it as simple as that, no further justification required. In his words [18] ,
The more terms we take, the less the difference becomes; and, consequently, if we continue the series to infinity, there will be no difference at all between its sum and … 2.
The concepts of infinity, of the limit, and of the infinitesimally small are discussed in more detail in Section 19.3 below.
In sum, close inspection reveals that, in the prime sequence, the primes relate to one another—or closely collaborate with one another, as it were—according to numerically definable principles. As a set of numbers, the primes present themselves as a truly close-knit and highly organized bunch. Their coordination is perfect. Their common design is to converge on a number involving π.
The prevailing notion that the primes wind their path through the positive integers aimlessly cannot be upheld. The evidence contradicts it. Nothing is more apparent than the extreme level of organization of the primes.
I therefore beg to differ with the following statement by L. Euler, as cited by D. Wells [19] :
Till now mathematicians have tried in vain to this day to discover some order in the sequence of prime numbers, and we have reason to believe that it is a mystery into which the human mind will never penetrate. To convince oneself, one has only to glance at the tables of primes which some people took the trouble to compute beyond a hundred thousand, and one perceives that there is no order and no rule.
9. Inaccessibility to Human Cognition of the Prime Sequence’s Highly Organized Patterns
Now that it has been established that the primes are extremely highly organized in certain ways involving π (additional ways will be adduced below), the next step is to search for an explanation of how these patterns of organization in question exactly work.
It is at this point that it becomes readily apparent that an explanation is inaccessible to human cognition. This inaccessibility pertains to both
1) infinity and
2) π, which in the end also involves infinity.
First, infinity. In the analysis in Euclidean fashion presented in Section 5, each number can be related to a line section of a certain length. All the line sections, each one corresponding to a prime, add up to a number involving π. This fact reveals an extraordinarily high level of organization.
In order to comprehend the relation between all these precise line lengths pertaining to primes, it is indispensable to know every single one of them.
However, nothing is more obvious than that these precise line lengths are infinite in number. It is therefore impossible for human intelligence to know them all. And knowing them all is a necessary condition for understanding certain highly organized patterns of organization—described above—in which every prime relates to every other prime, every prime relates to any set of two or more primes, any set of two or more primes relates to every other set of two or more primes, and any single prime or set of two or more primes relates to all the primes together.
Next, π. As the sum of the afore-mentioned precise numbers grows larger, it approaches ever more closely a number involving π. π is transcendental. As distinct from irrational numbers, transcendental numbers are not the root of another number. But the decimals of both irrational and transcendental numbers run on into infinity.
Each prime has been presented above in Euclidean fashion as corresponding to a precise line length. All the line lengths were counted cumulatively from a certain number. But there is another way of measuring lengths, namely in terms of distance from a number involving π, in the above case π2. These distances too are highly organized because each collaborates singly and jointly with all the others to make the sequence of primes reach an exact number involving π.
However, none of these latter distances can be known with precision because π cannot be precisely known even though it is a precise number. These distances are a direct reflection of the prime sequence. Because the distances stop at a number involving π, they end in an infinite number of decimals. Yet, in order to establish how all the primes work together, it is necessary to know the distances exactly as they get smaller and smaller.
How π can be a precise number and yet not be fully known is simply beyond human cognition. And so is by extension, according to the present line of argument, the prime sequence.
In any attempt to explain the prime sequence, the following consideration already mentioned above also applies.
Take the lowest primes, say, the sequence of just the first seven primes 2, 3, 5, 7, 11, 13, and 17. It has been common for mathematicians to search for ever higher primes containing millions of digits. The danger of these large scale endeavors is that one loses sight of the fact that a full understanding of the prime sequence needs to include an understanding of the simple facts that 11 is the next largest prime after 7 and that 13 is the next largest prime after 11.
It appears that, in relation to the facts presented above, the relation between 11 and 7 and the relation between 13 and 11 are but two links in a perfectly organized chain that runs on into all infinity, up to a number involving π.
Each link makes a contribution to the entire chain. If the contribution of any link were a little smaller or a little larger, the entire chain would be affected. Accordingly, each gap between two primes is exactly as it should be.
It also follows that it is necessary to know all the links in the chain to understand the relation between 11 and 7 and the relation between 13 and 11, or already between 2, 3, and 5. The distances between 2, 3, and 5 are part of a pattern that runs on into all infinity.
But the links in the chain cannot all be known. That is because there are infinitely many of them. Accordingly, it is not humanly possible to comprehend the highly organized behavior of the primes described above according to which 11 is the next prime after 7, 13 is the next prime after 11, and so on. Nor is it possible to compute the sequence of the primes according to a single overarching principle, in the sense that a single formula can be constructed that makes it possible to compute 11 as the next largest prime after 7, 13 as the next largest prime after 11, and so on.
L. Euler’s infinite prime product was converted above into a sum in order to imagine the addition of quantities spatially in Euclidean fashion. Such spatial imagery is not indispensable to the conclusion that the prime sequence is inaccessible to human cognition. The same can be concluded arithmetically by turning the product into a sum, with each term of the original product making a number larger by a certain quantity in a sum that ever increases.
Then again, there are in fact also infinite sums involving all the primes converging on a number involving π. An example is as follows:
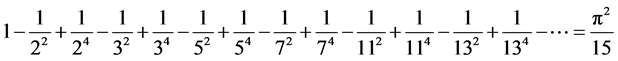 . (15)
. (15)
This is not my result. I have found it in the literature on the primes but neglected to note down the source. I will use the result again in what follows. The sum converges on about 0.658, starting from 1, through the addition or subtraction of an infinite number of quantities. Again, to understand how these quantities interact, one has to know all of them. But that is not possible because there are an infinite number of them.
10. Potential Objection to Assuming That the Prime Sequence Is at the Same Time Opaque and Highly Organized
One might object at this point by assuming that, while the highly organized patterns of the prime sequence described above cannot possibly be comprehensible, other highly organized patterns will perhaps be discovered in the future that do permit comprehension. Accordingly, the mystery of the prime sequence would finally be solved.
These other newly discovered patterns would presumably make the prime sequence computable. There would be a single theoretical principle or theory that explains why 19 is separated from 17 by 2, 23 from 19 by 4, and 29 from 23 by 6, and so on.
One might also assume that the size of the ratios of every prime over any other prime would be understood. An example is the ratios of any prime over the next smallest prime. The ratios are as follows:
 ,
,  ,
,  ,
,  ,
,  ,
,  , and so on.
, and so on.
These ratios increase or decrease in quantity with ever higher primes. A newly discovered pattern might be expected to explain these changes in quantity according to a single principle.
The problem with this assumption is as follows. It is a fact that the very same afore-mentioned distances 2, 4, 6, and so on, also allow the primes to converge on a precise number according to the following pattern and many like it:

It would follow that the very same, numerically extremely precise, sequence of distances or ratios would be opaque in one pattern, the one described above, and transparent in another newly discovered one. This seems like a contradiction.
In other words, the sequence 2, 3, 5, 7, 11, and so on, would be completely transparent by means of the newly discovered pattern but it would be opaque in the infinite prime product above.
The infinite prime product can be interpreted as a kind of function of the prime sequence, as follows:
 ,
,
in which p stands for “prime number”.
A newly discovered fully transparent pattern characterizing the prime sequence would explain the continuous change of p from 2 to 3 to 5 to 7, and so on, according to a single overarching principle or formula.
But at the same time, the continuous change in  or
or  would be explained because
would be explained because 
 is a function of p. In other words, the rate of growth of
is a function of p. In other words, the rate of growth of  would be explained by the rate of growth of p.
would be explained by the rate of growth of p.
One has every right to assume that a newly discovered transparent pattern involving the prime sequence ought
to make the pattern of convergence of the infinite prime product on  transparent.
transparent.
But as was noted above, the convergence pattern involves an infinite number of terms and the number π. The newly discovered pattern would therefore in a sense explain infinity itself and π itself!
I do not deem such a thing possible. Infinity cannot be truly grasped, at least not by the physical brain. Nor can it be explained why π is about 3.14 and not about 2.14 or about 4.14. Infinity and π are curtains, as it were, behind which rational human intelligence cannot look.
11. A Mathematical “Poem” Involving the Prime, Non-Prime, Uneven Number, and Even Number Sequences, and Its Relation to the Riemann Hypothesis
What is proposed above is that, while the prime sequence is organized, its organization cannot be understood by the human brain. There are additional indications that suggest the same. One of these indications is as follows.
All the interest in the prime sequence implies that there is something special about the primes and their sequence. I know of no similar efforts to seek a principle that explains the sequence of the non-prime or composite numbers, let alone the sequence of the uneven numbers or the sequence of the even numbers.
One speaks about the music of the primes. But what about the music of the non-primes? The non-primes are just one side of the coin the other side of which is the primes. In what follows, it will appear that the non-primes and the even and uneven numbers display some of the same music as the primes.
What follows suggests that the prime sequence may not be all that special at all.
Much of the interest in the primes revolves around the Riemann Hypothesis, described in Section 4. The Riemann Hypothesis is one manifestation of the belief that there is something special about the prime sequence. Many assume that proving the Riemann Hypothesis might reveal what is so special about the primes.
What is the connection between the prime sequence and the Riemann Hypothesis? The connection involves the fact that B. Riemann made the following Equation, discovered by L. Euler, into the “point of departure (Ausgangspunkt)” of the study in which he proposed what is now called the Riemann Hypothesis [20] :
 (4)
(4)
Evidently, this Equation makes an essential statement about the prime sequence.
In other words, the Riemann Hypothesis is ultimately derivative of—or subordinate to—the expression
 , (16)
, (16)
which involves the primes.
As was noted before, the Riemann Hypothesis is now widely accepted, even though everyone agrees that there is no proof of it and I personally doubt that there ever will be.
In any event, if the Riemann Hypothesis or a proof thereof reveals anything about the primes, then the revelation should most directly concern expression (16) as a pattern of organization and not some other pattern of organization because the Riemann Hypothesis is derived from (16). That seems only logical. Expression (16) is the source of the Riemann Hypothesis, as it were, in as far as the prime sequence is concerned.
However, as it happens, the design of the present article is to demonstrate, not only that expression (16) does indeed exhibit a form of organization, but also that this form of organization cannot be comprehended by rational human intelligence.
It follows that the Riemann Hypothesis, proven or not, cannot say anything about the prime sequence. Such is the logical conclusion from the preceding sections. The line of argument of the present paper did not set out to make this statement about the Riemann Hypothesis. But the statement in question is just what logically follows from the paper’s line of argument. If expression (16) is demonstrably opaque, then how could the Riemann hypothesis—proven or not—say anything comprehensible about it?
J. Derbyshire seems to evoke a general sentiment when he states as follows [21] :
It follows that all the properties of the prime counting function are coded, in some way, in the properties of ζ [that is, the Zeta Function]. A sufficiently close study of  will tell us all we want to know about π—that is, about the distribution of the primes.
will tell us all we want to know about π—that is, about the distribution of the primes.
I am taking a different position in this regard. I deem infinity and π, which involves infinite decimals, to be beyond the grasp of human cognition.
One manifestation of expression (16) and what it is equal to is as follows:
 . (17)
. (17)
The Riemann Hypothesis involves a special property of certain values of the Zeta Function. Because the Zeta Function includes expression (16) involving the primes, many assume that the Riemann Hypothesis or its proof might reveal that the prime sequence exhibits special status among number sequences. But this expectation is contradicted to a degree by the following Equations, featuring all the non-primes in (18), all the even numbers in (19), and all the uneven numbers in (20):
 (18)
(18)
 (19)
(19)
and
 . (20)
. (20)
Also of interest is the following Equation, which features all the uneven numbers that are not primes:
 . (21)
. (21)
It is explained in Section 12 below how these four Equations are obtained.
The four Equations (17), (18), (19), and (20) display in unison, as it were, a remarkable pattern of multiple symmetries, contrasts, and complementarities. It is a kind of mathematical poem of the integers of which the deeper meaning will forever elude us. It rhymes, as it were. The multiple stylistic and structural features of this poem are as follows:
1) All the four principal types of integers are represented: the primes in (17), the non-primes in (18), the even numbers in (19), and the uneven numbers in (20). The mathematical poem at hand comprehensively concerns all the integers and all the four main types of integers.
2) Pairing.—Two facts signify that the primes and the non-primes together form a pair and that the uneven and the even numbers do so too.
First, all four infinite products in (17), (18), (19), and (20) converge on a ratio involving π. But in the Equations pertaining to the even and the uneven numbers, the infinite products converge on the first power of π. By contrast, in the Equations pertaining to the primes and the non-primes, the infinite products converge on the second power of π.
Second, one member of either pair encompasses all the integers that the other does not. Or, each pair encompasses all the integers.
This much for the question as to which infinite product goes pair wise with which other infinite product.
The attention now turns to, a), the relations between the two members of each pair and, b), to the relations between the pairs. The former, a), are addressed in 3) and the latter, b), in 4), 5), and 6).
3) Complementarity between the Members of the Pairs.—As to the relations between the two members of each pair, there is what might be called complementarity. The two members of both pairs behave like two sides of a coin, as it were.
In Equation (17) concerning the primes, the squares appear in the numerator and the same squares minus 1 appear in the denominator. Exactly the opposite is the case with Equation (18) concerning the non-primes. As it has already been established that the primes and the non-primes are two members of the same species, it would appear that the property in question points to a certain type of complementarity of the two members inside each pair.
In Equation (19) concerning the even numbers, the squares appear in the numerator and the same squares minus 1 appear in the denominator. Exactly the opposite is the case with Equation (20) concerning the uneven numbers. As it has already been established that the even numbers and the uneven numbers are two members of the same species, it would appear that the property in question points to a certain type of complementarity.
4) Similarity of the Pairs Themselves.—As regards the relations between the pairs, there is similarity or repetition.
First, in both pairs, the result yielded by one member of the pair is twice as large as that yielded by the other member. The result of the infinite product of primes in (17) is twice as large as the infinite product of non-primes in (18). And the result of the infinite product of even numbers in (19) is twice as large as the infinite product of uneven numbers in (20).
Second, the complementarity described in 3) is of the same type in both pairs, involving the relation of squares to the same squares minus 1.
5) Complementarity between the Pairs Themselves.—Is there a way of viewing the primes or the non-primes as being complementary with either the uneven or the even numbers?
In 3) above, it was noted that the contrasting positions in the numerator and the denominator of squares and the same squares minus 1 suggests complementarity.
The same contrasting positions now suggest complementarity between the prime numbers and the uneven numbers, on the one hand, and between the non-prime numbers and the even numbers, on the other hand.
In addition, (21) suggests that the primes also exhibit the same type of complementarity with the uneven numbers that are not primes.
This complementarity between the pairs can ultimately not be fully understood by the human brain. But there is another fact that points to a certain complementarity.
The fact concerns what primes and uneven numbers, on the one hand, and non-primes and even numbers, on the other hand, share in terms of partition. The matter of partition and the primes is discussed in more detail in Section 16 below. The position will be taken that the problem of the primes and the non-primes viewed jointly as two sides of a coin is also about the concept of partition. I have not found the primes and non-primes studied in terms of partition theory.
Primes owe much of their lofty status in mathematics and also in the popular imagination to multiplication and factors. According to the fundamental theorem of arithmetic, every number is either a prime or a unique product of primes, 1 not being a prime and disregarding the order of the primes. For example,
 . (22)
. (22)
No other number evidently exhibits this same product of primes. And it is possible to prove it in more than one way.
That means that the primes can be seen as the numbers from which all the non-primes are constructed. The primes can therefore metaphorically be regarded as a kind of building blocks of nature.
But in the end, multiplication is just an abbreviation of addition. Multiplication is derivative of addition, as follows:

is nothing other than
 (23)
(23)
or
 . (24)
. (24)
In the abbreviation, information is lost in that the distinction between (23) and (24) is obliterated. Clearly, three couples is not the same as two threesomes, as it were.
Again, multiplication is a secondary and derivative concept. This is also a reason why I have preferred above to interpret primes in terms of additions of quantities, as expressed in Euclidean fashion by lengths of lines, and not in terms of multiplication.
Partition is all about addition. Accordingly, the right-hand side of (22) can be partitioned in three ways. The three ways correspond to 2 × 2 × 5, 2 × 5 × 2, and 5 × 2 × 2 on the assumption that order makes a difference, which it otherwise does not in multiplication.
Expressed by means of addition, the three ways in question are as follows:

It is in fact the mathematical concept of partition that led to the writing of the present paper. Partition itself had come to my attention in the course of my study of probability. And ever since G. Boole, probability matters to the study of rational human intelligence because half of it is digital mathematics.
More about partition in Section 16 later. How is partition relevant to the present line of argument?
The contrast between even numbers and uneven numbers and the contrast between primes and non-primes can both be defined by the concept of partition.
The contrast between even numbers and uneven numbers is between presence and absence of partition into equal groups of 2.
The contrast between primes and non-primes is between presence or absence of partition into any kind of equal groups.
In that regard, one might say that the primes are hyperuneven and the non-primes hypereven. More on the concepts hyperuneven and hypereven follows in Section 18.4.
It appears that both primes and uneven numbers exhibit absence of their respective defining partitions and that both non-primes and even numbers exhibit presence of their respective defining partitions.
When it comes to any kind of partition, it appears that primes always exhibit partition whereas non-primes and even numbers never exhibit partition. Uneven numbers are the odd man out. They can or cannot exhibit partition.
In regard to presence or absence of partition, the exact complement of primes is uneven numbers that are not primes. It so happens that Equation (21) confirms that there is complementarity between the two in regard to the position of squares and the same squares minus 1.
6) Similarity of the Complementary Pairs.—This similarity involves the multiplication of the infinite prime product in (17) with the infinite uneven product in (20), on the one hand, and the multiplication of the infinite non-prime product in (18) with the infinite even number product in (20), on the other hand. Remarkably, the result is the same, as follows:
 .
.
Or the following applies:
 .
.
A pattern involving all the primes and all the uneven numbers yields the same result as a pattern involving all the non-primes and all the even numbers.
In sum, from 1), 2), 3), 4), 5), and 6) above, it is difficult to escape the impression that some grand poetic harmony is at work here. There is more than the primes running 2, 3, 5, 7, 11, 13, and so on, than the non-primes running 4, 6, 8, 9, 10, 12, and so on, than the even numbers running 2, 4, 6, 8, 10, 12, and so on, and than the uneven numbers running 3, 5, 7, 9, 11, 13, and so on. They can all four together in their totality be seen to obey
a single architecture culminating in 6) in the all overarching number .
.
It may seem frustrating that this harmony involving number sequences is inaccessible to the human brain. Then again, inaccessible high patterns of organization involving number sequences is what this paper is all about.
The harmony described above and others like it (see below) make another crucial point that is specific to the present section.
In the grand harmony in question, the primes do not occupy a special place. They are just a cog in a much larger wheel. The roles played by the non-primes, the even numbers, and the uneven numbers are equally important. Yet, again, no one ever seems to worry about these three sequences. Everyone seems to accept them as completely self-explanatory. But what about the music of the non-primes, the music of the even numbers, and the music of the uneven numbers? Do they have a right to a hearing?
The impression that arises from the above is of a much grander scheme that far transcends the scope of the prime sequence. There is nothing special about the prime sequence in this grander scheme.
Before pointing to some other indications of a certain unexceptionality on the part of the prime sequence, it will be useful to describe how Equations (18), (19), (20), and (21) have been obtained. I have not been able to find them anywhere. But the literature on number theory is immense.
12. How the Mathematical “Poem” Is Obtained
12.1. Equation (18)
Equation (17) shows how an infinite product involving all the primes converges on a certain number. It follows evidently that, if one knows to which number the corresponding infinite product involving all the natural numbers converges, then dividing the result for all the natural numbers by the result for all the primes will yield the result for all the non-primes.
It appears that the infinite product of the same type as L. Euler’s infinite product, but involving all the natural numbers except 1, is known. The fact is not too difficult to obtain. But I have not found it reported anywhere.
The infinite product of the same type involving all the natural numbers is as follows:
 .
.
However, the denominator includes , which is equal to 0. The entire denominator is therefore equal to 0. And dividing by 0 is considered undefined.
, which is equal to 0. The entire denominator is therefore equal to 0. And dividing by 0 is considered undefined.
The problem is easily resolved by excluding 1. In other words, the natural numbers without 1 exhibit coherence as a set.
The exclusion of 1 could be seen as supporting Euclid’s assumption in Definitions 1 and 2 of Book VII of his Elements that 1 is not a number. It is rather the “unit” (Greek monas) by which “numbers” (Greek arithmos), that is, positive integers or natural numbers larger than 1, are “composed” (Greek sugkeimenos) and with which everyone of them is “being measured” (Greek metroumenos).
It will be wise to recall—as has been done above—that, for more than 2300 years now, no one has ever bet against Euclid and won.
The desired infinite product is therefore as follows:
 (25)
(25)
An equivalent expression is evidently as follows:

Or also:
 .
.
This expression can be rewritten as follows:
 . (26)
. (26)
And therefore also as follows:
 .
.
It thus appears that the following Equation applies:
 . (27)
. (27)
It is evident that the result of the infinite product in (25) is 2. If one considers (26), it appears that the infinite product cannot quite be said to converge on 2 in the sense of ever coming closer to 2. It is rather that a distance away from 2 created by multiplication with one fraction is instantly annulled by multiplication with the next fraction.
Then again, there is a way of presenting (25) so that it can be seen converging, namely as follows:
 (28)
(28)
Equation (28) begins at  and gradually inches upward. It is not clear from just looking at (28) that it con-
and gradually inches upward. It is not clear from just looking at (28) that it con-
verges on 2. But the derivations presented above show that it does.
Dividing Equation (27), which involves all the natural numbers except 1, by Equation (17), which involves all the primes, looks as follows:

Eliminating the terms common to numerator and denominator yields the following result involving all the non-primes:

This Equation can also be written as follows:

A more analytical presentation is the following:

L. Euler’s infinite prime product in Equation (17) begins at  and converges upward on
and converges upward on . The corresponding inverted infinite product of all non-primes begins at
. The corresponding inverted infinite product of all non-primes begins at  and converges downward on exactly half that, namely
and converges downward on exactly half that, namely .
.
Viewed in this manner, the non-primes are seen winding their way through the positive integers or natural numbers in a manner that is exactly the same as the primes, in the following way. Forming fractions together with natural numbers larger by 1 or smaller by 1, they converge by means of an infinite product on a number including π2 in the numerator.
What is more, the infinite prime product and the infinite non-prime or composite product behave in a way as 2 does to 1. One is larger than the other by a factor of 2.
It is the behavior of the prime sequence that has traditionally gotten all the attention. However, any effort to explain the pattern of the prime sequence must at the same time explain the pattern of the non-prime or composite numbers. The prime sequence cannot be studied in isolation. The problem of the primes is a problem of all the numbers in their totality. And what is more, it appears from the above that the two sequences, as mirror images of one another, lead to a similar type of result.
12.2. Equations (19) and (20)
Equations (19) and (20) can be inferred fairly directly from the following Equation first established by J. Wallis in his Arithmetica infinitorum of 1655:
 (29)
(29)
The following two equivalent presentations will readily show that J. Wallis’s infinite product is of the same general type as L. Euler’s infinite prime product.
A first equivalent of (29) involving all the even numbers is as follows:

L. Euler might also have written this as follows:
 . (30)
. (30)
A second equivalent of (29) involving all the uneven numbers is as follows:

Or also as follows:

L. Euler might have written this as follows:
 . (31)
. (31)
Or maybe as follows:
 (32)
(32)
If one multiplies (30) with (32), one obtains an infinite product involving all the natural numbers except 1, whose result—already obtained above in a different way—is 2, as follows:
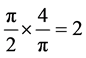 .
.
It has already been noted in Section 12.1 that, as far as infinite products of a certain type first proposed by L. Euler are concerned, the primes relate to the non-primes or composite numbers as 2 does to 1. Now it appears that the even numbers relate to the uneven numbers also as 2 does to 1.
It may be noted that 1 is excluded from (30) and (31) just as it is from (17) and (18), again a confirmation of sorts of Euclid’s view that 1 is not a number, or is at least to be categorized as being in some way fundamentally different from the integers larger than 1.
12.3. Equation (21)
Equation (21), featuring an infinite product running over all the uneven numbers that are not primes, is obtained by multiplying Equation (17) by Equation (31), as follows:
 (33)
(33)
After elimination of the common factors in numerator and denominator, Equation (33) can be rewritten as follows:
 (34)
(34)
The fraction  has already played a role in Section 11.
has already played a role in Section 11.
Equation (34) can also be rewritten as follows:

And also as follows:

This is the desired infinite product involving all the uneven numbers that are not primes.
13. Variations Related to the Mathematical “Poem”
In the numerical architecture described in Sections 11 and 12 above, the prime sequence is not endowed with special status among the main number sequences.
Absence of special status on the part of the primes also characterizes the following Equation:
 (35)
(35)
Equation (35) can also be written as follows:

This Equation is obtained by multiplying Equation (17) by Equation (18). In Equation (35), the primes and the non-primes display their distinct identities as follows. The squares of the primes appear in the numerator and the squares of the non-primes in the denominator. The opposite is the case for the squares minus 1.
Equation (35) shows the primes and the non-primes collaborating, as it were, towards a common a goal. In this process, the primes and the non-primes appear to have equal status, complementing one another.
Similar complementation of the primes and the non-primes can be found in the following Equation:
 (36)
(36)
A plus sign accompanies the primes; a minus sign, the non-primes. The infinite product of fractions can be inverted because the product equals 1. Equation (36) represents a novel way of defining the number 1. It can also be written as follows:

Equation (36) is obtained as follows. One takes as point of departure the value of L. Euler’s infinite prime product when the exponent is 4, namely the following:
 (37)
(37)
One next inverts Equation (37) and multiplies the inversion of (37) by Equation (35) above. This means that the fractions pertaining to the non-primes in (35) survive as they are. By contrast, each fraction pertaining to a prime is multiplied by a second fraction pertaining to the same prime. In the case of the prime 2, the resulting product is as follows:
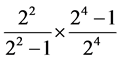 .
.
And therefore also as follows:
 .
.
Elimination of the common terms produces the following result:
 .
.
And so likewise for all the other primes.
The result of multiplying the inversion of (37) by Equation (35) is therefore as follows:

Or also as follows:

And transferring  to the other side of the Equation yields Equation (36). As was noted, inversion of (36)
to the other side of the Equation yields Equation (36). As was noted, inversion of (36)
produces the same result because the result equals 1.
There are countless related infinite products. But there are also countless related infinite sums. The following example has already been cited at the end of Section 9:
 (15)
(15)
This product concerns the primes. It can also be written in a form that resembles (37) more closely, namely as follows:

The corresponding infinite product involving all the non-primes is as follows:
 (38)
(38)
Equation (38) is obtained as follows. The following Equation applies:
 (39)
(39)
The search for the solution of the infinite sum in (39) is known as the Basel problem. As was already noted, L. Euler solved it.
Adding (39) to (38) yields the following result:
 (40)
(40)
The following Equation also applies:
 (41)
(41)
This is (39) with exponent 4 instead of 2.
Subtracting (41) from (40) yields (38), which is the Equation sought.
Equation (38) can also be written as follows:

Adding (41) to (40) yields the following result

In this Equation, primes and non-primes exhibit contrasting behavior.
Once again the primes do not seem special since the non-primes behave in the same way.
Similar behavior can be seen in the following infinite sum involving the uneven numbers, discovered independently by both G. W. Leibniz and J. Gregory [22] :
 .
.
14. Is the Prime Sequence Special?
14.1. From Primes to Primes-cum-Non-Primes and Back to Just Primes
According to the material presented in the preceding sections, there seems to be nothing special about the prime sequence in its relation to other number sequences. Then again, there are opportunities to observe the possibility of prime primacy, so to speak. It is not entirely clear what to make of it. In any event, any hints at the primacy of primes also are subject to the observations already made above. The primacy involves the factor of infinity in a way that makes its comprehension inaccessible to human cognition.
Results for the non-primes such as (18) and (38) were derived from the behavior of the primes and not vice versa. Does this point to a certain primacy of the primes over the non-primes? Whatever may be of the matter, for the reasons already laid out above involving the dimension of infinity and π, comprehension of such primacy by the human brain would be impossible because it involves the factor of infinity.
An inexplicable prime primacy affects the following Equation already discussed above:
 (35)
(35)
The primes and the non-primes appear to exhibit a balanced relation. Still, the behavior of the non-primes in (35) has been derived from the behavior of the primes (see above).
So it perhaps comes as less of a surprise that, if one makes all the fractions explicit and eliminates all the terms common to numerator and denominator, one obtains a different result that exclusively involves the primes.
The fractions are as follows:

Elimination of the common factors yields the following result:
 (42)
(42)
The non-primes in the denominator are all adjacent to primes. Since a non-prime between twin primes—that is, primes separated by 2—are adjacent to two primes, they receive the exponent 4 and not the exponent 2.
Equation (42) is the desired expression involving exclusively the primes. How so?
It appears that the left-hand side of (42) can be rewritten as follows:

And therefore also as follows:

Or also as follows:

As one can see, only the primes are involved in this expression.
What about the special behavior of 2 and 3? It is clear that, 1), 3 is adjacent to only one non-prime and not to two non-primes like the primes higher than 3, and that, 2), 2 is adjacent to no non-prime if, like Euclid, one excludes 1 as a number. This structural principle seems reflected in the following equivalent of (42):

The behavior of the square of 3 somehow seems indicative of the fact that it is bordered on only one side by a non-prime, the plus side.
Primes bordered on two sides exhibit the exponent 4 in (42). It therefore somehow seems natural that 3 exhibits the exponent 2, or half of 4.
Then again, the behavior of 3 can be made to look exactly like that of the higher primes by means of the following suggestive equivalent of (42):

And in fact, in the following equivalent of the left-hand side of (42), every single prime can be seen behaving in the same way, accompanied in the numerator by the number that is one smaller and the number that is one larger:

This means that another equivalent of Equation (42) is as follows:

This Equation is all about primes in the denominator and numbers that are one more or one less than a prime in the numerator.
Or also as follows:

This Equation is all about the primes in the denominator and numbers that are one more or one less than a prime in the numerator, but excluding 1 as a number with Euclid.
One is reminded of an Equation already adduced above, the following:
 (18)
(18)
This Equation can be rewritten as follows:

This Equation is all about the non-primes in the denominator and numbers that are one more or one less than a non-prime in the numerator.
If one compares the two afore-mentioned Equations

and

and also realizes that
 ,
,
then it appears that squaring a result involving all the non-primes (and all the numbers one smaller or larger) in the first power yields a result involving all the primes (and all the numbers one smaller or larger) in the second power. It is a bit as if squaring the non-primes yields the primes.
One is once more reminded of being in the presence of a number harmony. But again, the harmony takes place in the dimension of infinity. The deeper nature of the harmony is therefore not accessible to rational human intelligence.
The whole matter just again and again keeps evading and eluding rational human intelligence. But who would dare to state that rational human intelligence knows no boundaries and is as large as the universe itself?
14.2. Variations on L. Euler’s Infinite Prime Product and Prime Primacy
Another case in which a certain prime primacy may possibly be discerned is as follows. Again, if there is indeed prime primacy, then it is at the same time obvious that the organized behavior is not accessible to human cognition.
This second case involves L. Euler’s infinite prime product, which is as follows:
 (4)
(4)
Values involving fractions that include integers and π can be determined for all even powers. The first are as follows:



and so on.
Since B. Riemann expanded L. Euler’s infinite prime product and named it the Zeta function, it is customary to refer to the results above as ,
,  ,
,  , and so on. Higher values can be found on the Internet [23] .
, and so on. Higher values can be found on the Internet [23] .
It is also possible to establish values for an infinite prime product that differs from the one above only in that one finds plus where the product above has minus. It may be called the infinite prime product-plus. The first values are as follows:


exponent 6: 
exponent 8: 
exponent 10: 
exponent 12: 
exponent 14: 
exponent 16: 
exponent 18: 
and so on.
I submitted the sequence of the integers in the numerators and the sequence of the integers in the denominators of this infinite prime product-plus to the Online Encyclopedia of Integer Sequences (www.oeis.org), computed in longhand, in the fall of 2013 and they were accepted as sequences A231273 and A231327. The website administrators have computed and added values for higher exponents.
Another infinite series is also related to L. Euler’s prime product. It may be called the infinite prime product-minus-plus. It is as follows:
 ;
;
 ;
;





and so on.
It was in order to submit these sequences that I originally for the first time consulted www.oeis.org. A search quickly revealed that B. Cloitre had already submitted them in February of 2006. They are sequences A114362 and A114363. The proof provided below indicates that I reached the same results independently. No explicit proof is otherwise provided for A114362 and A114363 on www.oeis.org. Therefore, I do not know at this time whether there is another way of providing proof.
B. Cloitre notes, as a remarkable property of the results of the infinite prime product-minus-plus, that they are rational. The reason for this property is explained below.
The infinite prime product-plus and the infinite prime product-minus-plus are obtained as follows.
Consider the expression
 , (43)
, (43)
which is one manifestation of L. Euler’s infinite prime product, namely
 . (44)
. (44)
Expression (43) evidently equals
 (45)
(45)
One manifestation of (44) is
 . (46)
. (46)
Dividing (45) by (46) obviously, after simplification, yields a manifestation of the desired infinite prime product-plus, namely
 . (47)
. (47)
But on what does (47) converge? In order to obtain (47), (45) was divided by (46). It so happens that it is known on what (45) and (46) converge. All that one needs to do, therefore, is to divide the number on which (45) converges by the number on which (46) converges. (45) is commonly styled as  and (46) as
and (46) as . It is well-known and has already been noted above that
. It is well-known and has already been noted above that

Evidently, dividing (45), or , by (46), or
, by (46), or , yields
, yields .
.
The same reasoning applies to the relation in general between

and
 .
.
All the manifestations of the infinite prime product-plus converging on a number involving π are therefore obtained by the following division:
 .
.
QED.
The manifestations of the infinite prime product-minus-plus converging on a number involving π are obtained by dividing (47) by (46). The division in question looks as follows:

Since (47) is itself the result of dividing (45) by (46), dividing (47) by (46) is in effect the same as dividing (45) by the square of (46). The procedure can be presented as follows:
 .
.
The actual values are as follows:
 . (48)
. (48)
The procedure can be generalized as follows:
 .
.
Other values for  have already been listed above.
have already been listed above.
It appears that (48), in which , is a ratio between two fractions that both feature π4 in their denominator. The factor π4 is therefore eliminated. What is left is a rational number.
, is a ratio between two fractions that both feature π4 in their denominator. The factor π4 is therefore eliminated. What is left is a rational number.
In conclusion, it is because the infinite prime product-minus-plus is a ratio of two fractions with the same numerator π4 that its results are rational.
In Section 11, the infinite non-prime product was determined for exponent 2, as follows:
 (18)
(18)
But it is not clear whether the results for exponents higher than 2 are similarly elegant, probably not.
The procedure to establish (18) for exponent 2 in Section 12.1 could not be used because no usable result could be obtained for the following expression when n > 1:

Only a minor marginal result was obtained for the following expression, in which n = 2:
 . (49)
. (49)
This expression is evidently the same as the following:

It has already been noted in Section 12.1 above that the first product of the two infinite products in this expression equals 2. Expression (49) therefore is the same as
 .
.
Therefore, the following Equation applies:
 (50)
(50)
It appears that, by squaring the exponents and by changing the sign from − to + in
 ,
,
one obtains a result that is exactly twice as large.
The left side of Equation (50) is an infinite product beginning at  and increasing. The right side is an infi-
and increasing. The right side is an infi-
nite product beginning at 2 and decreasing. It is obvious that both infinite products converge on the same number from two directions. They meet at roughly 1.1.
It can be concluded that certain types of results that can be obtained for primes cannot be obtained for non- primes. Is this an indication of prime primacy? If it is, the main point of the present article is once again illustrated, namely that there is abundant evidence of organization in number sequences such as the prime sequence; but also that all this patent organization is not accessible to human cognition.
15. Aristotle and the Limits of Rational Human Intelligence
Aristotle writes as follows about axioms in his Metaphysics, at 4.3.9 and 4.4.2 [24] .
A single thing cannot at the same time possess and not possess the same attribute all being the same. … That is the firmest of all axioms. …
Some ask for proof, but only because they lack education. Proving everything is definitely impossible. One would just recede into infinity [that is, in trying to prove everything by something else]. (My translation.)
Distinctions are the stuff of which knowledge is made. Aristotle makes three distinct statements about axioms.
First, more specifically, he describes an axiom, the one that he deems to be the most fundamental one of all. It is also known as the fundamental axiom, or law, of thought.
After Aristotle, it became common to think of the existence of three fundamental axioms of thought.
1) The Principle of Identity, as in “A cow is a cow”.
2) The Principle of (Non-)Contradiction, as in “Something cannot be both a cow and not a cow at the same time”.
3) The Principle of the Excluded Middle, as in “Something is either a cow or not a cow”.
The Principle of Contradiction is closest in formulation to Aristotle’s sole fundamental axiom of thought.
I intend to present a detailed treatment of the fundamental axiom(s) of thought elsewhere.
The second, more general, statement that Aristotle makes in the passage quoted above is that there must be such a thing as axioms. It is a kind of “proof of unprovability (Unbeweisbarkeitsbeweis)” [25] .
Nothing seems more evident. A proof of a theorem requires given and accepted observations that are outside that theorem. But if the accepted observation is itself always a theorem, there could be no end to the proof. Each time that one stops at a certain theorem, one would not be finished because the theorem in question would also need to be proven by yet another theorem. Without axioms, proofs would need to run on into infinity, which is impossible.
It may be assumed that the number of theorems, however large it may be, is limited.
To keep things simple, let us assume that there are just five theorems, A, B, C, D, and E. Let us assume that A is proven by B, B by both C and D, and D by E. But then there is no proof for C and E. And one cannot prove C or E by A, B, or D because that would be circular reasoning. C or E already prove A, B, or D.
However many arrangements one comes up with, at least one theorem ends up without a proof. The same may be assumed if one could consider all the theorems of mathematics all at once. There is no reason why things would be any different from what one finds in the above simple scenario.
Aristotle’s statement sounds a lot like K. Gödel’s Incompleteness Theorem. Is there more to the Incompleteness Theorem than what Aristotle stated already more than two millennia ago?
The third statement concerns the order of the axioms. In that regard, the fundamental axiom of thought stands at the very beginning. It does not even depend on another axiom.
What does this mean for the prime sequence? If something outside the sequence explains it, then that would still need to be explained by something else.
Or perhaps, many tacitly assume and hope that the deepest structure of the Book of Nature would be magnificently revealed if the prime sequence can be explained, for example, by proving the Riemann hypothesis. But I believe that this is not possible. The brain is a finite material tool. It can do certain things. But it is certain that there are things that it cannot do. Therefore, there is a line between the two. That line is the final frontier of the brain’s limitations.
The thesis of the present paper is that nothing can explain the prime sequence. But even if one assumes for the sake of the argument that something could, then what explains it would still require an even deeper explanation. In other words, there are no final explanations of nature accessible to the limited physical brain in its current state.
This approach makes it also easy for the physical brain to be completely comfortable inside its absolute limitations once it realizes that there simply must be limitations to something that is physically finite.
This approach makes what are considered abstruse mathematical concepts delightfully simple. Consider infinity. My own view is that nothing is easier to understand than infinity. Additional remarks on infinity and the pesky concept of the infinitesimally small follow in Section 19.2.
What about infinity? The matter is simply this. However great a certain number may be, one can always add 1 and make it bigger. And one can just keep doing this. There is no reason to stop. What could be more obvious?
As regards space, one can always extend a line. How else could it be? What could be simpler?
This approach makes it easier to come to terms with the prime sequence.
The identity of the primes is axiomatic. That is clear, as has already been pointed out above. What is easier to accept than that 17 is a prime? An axiom is an observation that is so abundantly obvious that no one sees a need for a proof. One simply accepts it without proof. Everyone agrees without proof that, say, 7 and 11 are primes. I personally know of no one who has ever asked for a proof that 7 and 11 are primes. That makes their identity an axiom. And that is also how Euclid appears to treat their identity (see below).
It is true that, in terms of identity, it becomes ever more difficult to identify ever higher primes. Does this make the prime sequence less than abundantly obvious and therefore less of an axiom? It does not. The difficulty with finding ever higher primes has to do with limitations of human intelligence and, beyond that, of computing power. If one had all the time in the world if not more and boundless intelligence, one could establish very high primes by the very same principles by which one establishes that 7 and 11 are primes.
Physicists have long stopped looking for final causes and perhaps mathematicians should likewise become a little less ambitious. In his Mécanique analytique (2nd edition 1811), J.-L. Lagrange “emphasized the laws connecting phenomena and he makes no attempt to search for a final cause of the phenomena” while “[p]rior to Lagrange a great deal of effort is spent uselessly by scientists in the search for final causes” [26] .
In his Mécanique analytique, J.-L. Lagrange writes, as translated from the French [27] :
The purpose of this work is to reduce mechanics to purely algebraic operations.
J. C. Maxwell’s theory of electromagnetism is complete, yet J. C. Maxwell did not know what an electron is.
In sum, I am at peace with the notion that the prime sequence exhibits a perfect structure that I will never be able to understand.
Much of what has been written above involves infinite series. Infinite series expose much—one might even say, an infinite amount of—organized behavior on the part of the primes, the non-primes, the even numbers, and the uneven numbers, and so on. But it reveals this behavior only in the dimension of infinity, which is inaccessible to human cognition.
Infinite series have played an enormous role in the development of mathematics since early modern times. They have revealed many truths. But the series also imply by their very nature that these truths are located in the dimension of infinity.
16. Partitions, the Primes, and the Prime Sequence
16.1. What Are Partitions?
The concept of partitions has already been introduced and briefly described in Section 11 above. It is my impression that the organization of the primes should have something to do with partition. Yet, I have so far not been able to find any reference to partition in connection with the prime sequence in standard descriptions of number theory (including those by G. E. Andrews, T. Apostol, U. Dudley, G. H. Hardy and E. M. Wright, E. Lucas, O. Ore, and others).
For example, in the chapter on partitions in G. H. Hardy’s and E. M. Wright’s survey of number theory, I cannot readily find the word “prime” mentioned even once [28] . Then again, the literature on number theory is enormous.
The reason for the absence may well be that, while the concept of partitions must be relevant to the prime sequence, it appears upon closer inspection that there is little or nothing that partition theory can say about the prime sequence at this stage. And it seems probable that partition theory never will, even if primes have everything to do with partition. In that regard, the concept of partitions supports the notion maintained in the present article that the organization of the primes is ultimately not accessible to human cognition.
What are partitions? Partitions are a property of numbers. They are the ways in which an integer can be equated to, or partitioned into, sums of integers. Partitions are therefore in effect sums and might be called partition sums. Partition(s) theory is the branch of mathematics that studies partitions.
An easily accessible introduction to partitions by J. Tanton, who has announced a book on the subject, is available on the Internet [29] . I adopt a number of general observations from his account in what follows.
For example, there are four ways of partitioning the integer 4 if order is not considered important. The resulting partitions or partition sums are as follows:

If order is taken into consideration, there are eight partitions, as follows:

Partition theory is not just about identifying all the specific partition sums. Partition theory is concerned mainly with ways of determining by means of general formulas how many possible partitions there are.
That does not only involve determining how many partition sums there are in general but also how many there are of a certain type. The distinction again applies between disregarding order or taking it into consideration.
The problem of partition theory that attracts perhaps the most attention—not in the least because it has not been solved—is determining how many partitions there are in general of a given integer n if order is not important.
The desired number is signified by the expression . Thus, in the example mentioned above,
. Thus, in the example mentioned above, .
.
S. Ramanujan first guessed, and then later proved together with G. H. Hardy, that  is approximately
is approximately
 .
.
An example of a type of question for which partition theory does offer a solution is as follows [30] : In how many ways can 12 be partitioned into sums of three sum components? There are 12, as follows:
 ,
,  , and so on.
, and so on.
This question calls to mind indeterminate algebra and Diophantine Equations. But this is not the place to elaborate on the matter.
Another question that has been answered in general and involves types of partitions is as follows: How many partition sums contain all even numbers or how many contain all uneven numbers? The number of integers is infinite. No precise numbers can therefore serve as the answers to these questions.
Instead, L. Euler proved that there are as many partitition sums involving all even numbers as there are partition sums involving all uneven numbers, without however providing a formula to determine how many exactly there are of both.
Interestingly, L. Euler used infinite series in his proof. The present paper proposes that no formula can be found for the prime sequence because the organization of the primes plays out in the dimension of infinity, which is not accessible to human cognition.
L. Euler’s afore-mentioned proof likewise suggests, in my opinion, that certain questions about partition theory such as how many partition sums there are in general or of certain types will never be answered because the deeper truths that should be the answers to the questions play out in the unreachable dimension of infinity.
Primes may well be the subject of one such question. Primes are integers that have no partition sums consisting of two or more equally large sum components, excluding 1 as a possible sum component. More on this below.
The question that partition theory might ask about primes is therefore as follows: Can it be determined on the basis of one formula whether a certain integer can or cannot be partitioned into equally large sum components? Those that cannot be would be the primes.
Partition theory seems like a vast area of mathematics in which so much still needs to be discovered. Or perhaps it is a much smaller area than may be assumed because so much will forever remain opaque.
The term “partition theory” is typically reserved for a branch of number theory. It is all about dividing numbers into types of sums.
However, beyond number theory, an integer can refer to a number of things in reality. These things can all differ from one another. What is more, these things can come in different orders or arrangements. And the question may be asked in how many ways a certain number of things can be arranged.
In this case, the number of partitions can be determined exactly. Combinatorics plays a role in determining the numbers. Combinatorics is the field of mathematics that teaches one in how many ways 12 people can sit on 12 chairs. The answer is 12! (“12 factorial”), that is,  , or 479,001,600 ways.
, or 479,001,600 ways.
The first person can sit on 12 different chairs. In each of these 12 different ways of sitting, 11 chairs are left and the second person can therefore sit on 11 different chairs. In other words, for each of the 12 ways in which the first person can sit, the second person can sit in 11 ways. The number of ways in which both can be seated is therefore 12 × 11. And so on for the third person and all the other persons.
It is easy to see the difference between partitions and the problem just discussed. The people seated on the chairs are not partitioned into groups, such as 5 (persons) + 3 (persons) + 2 (persons).
A question involving combinatorics that does exhibit similarity with the partition theory component of number theory is as follows: In how many ways can one hang 20 flags on 12 poles to broadcast different signals? The assumption is that there may be poles without flags.
The answer is
 ways,
ways,
that is,
 ways,
ways,
or
 ways,
ways,
and also
205,999,445,200,465,037,721,600,000 ways.
How is this answer obtained?
It is with the flags hanging on the poles as with the persons seated on the chairs above. The way of arranging 20 flags in a sequence is 20!. But there is more to be arranged than just the flags.
The sequence of the flags may be disrupted by a shift from one pole to the next. So the beginning of a sequence may be as follows: flag, flag, pole shift, flag, pole shift, and so on. That means that there are 2 flags on the first pole and 1 flag on the second pole. The beginning of another sequence is as follows: flag, flag, flag, pole shift, flag, flag, flag, pole shift, and so on. That means that there are 3 flags on the first pole and 3 flags on the second pole.
Between 12 poles, there are 11 shifts of poles. It appears that 20 flags and 11 pole shifts need to be arranged, or 31 items. If the 31 items were all different, as is the case with the persons seated on the chairs above, the number of the arrangements would be 31!
But whereas the 20 flags are all different, the 11 pole shifts are all the same. It is therefore necessary to divide 31! by 11! according to a well-known procedure of elementary combinatorics, which I will not discuss in detail here.
It was noted above that . For let the reference be to four flags. There are five ways of partitioning four flags if order is not important: 1), all 4 together, 2), 3 + 1, 3), 2 + 2, 4), 2 + 1 + 1, and 5), 1 + 1 + 1 + 1.
. For let the reference be to four flags. There are five ways of partitioning four flags if order is not important: 1), all 4 together, 2), 3 + 1, 3), 2 + 2, 4), 2 + 1 + 1, and 5), 1 + 1 + 1 + 1.
How does the classical partition problem exemplified above by —or that 4 flags can be partitioned in 5 ways—differ from the problem involving 20 flags and 12 poles? One difference is that arrangement of the flags, the sequence in which they come, plays no role in the classical partition problem whereas it does in the problem involving 20 flags and 12 poles.
—or that 4 flags can be partitioned in 5 ways—differ from the problem involving 20 flags and 12 poles? One difference is that arrangement of the flags, the sequence in which they come, plays no role in the classical partition problem whereas it does in the problem involving 20 flags and 12 poles.
By arrangement, I do not mean order of the quantities of the flags, in that arranging 5 flags on a first pole and 10 on a second is different from arranging 10 on the first and 5 on the second.
To get closer to the classical partition problem, arrangement may be made irrelevant. This means that the difference between placing flag a above flag b on a pole and placing flag a below flag b on the same pole does not make for a different signal.
In how many ways can 20 identical flags be placed on 12 poles if arrangement is irrelevant?
The answer is:
1220 ways
or
3,833,759,992,447,475,122,176 ways,
evidently fewer than when arrangement matters.
If f is “flags” and p is “poles”, the general formula is as follows:
 .
.
How so? Each of the 20 flags can hang on each of the 12 poles. If there were just 2 flags, the first could hang on each of the 12 poles and so could the second. Just as 3 men can combine with 3 women to form 9—or 3 × 3—possible couples, the 12 possible positions of the first flag can combine with the 12 possible positions of the second in 144—or 12 × 12—ways. These 144 combinations can combine with the 12 positions of the third in 1728—or 144 × 12—ways.
Evidently, one needs to multiply 12, the number of positions of one flag, as often with itself as the number of the flags, that is, 20. The total number of the combinations is therefore 1220.
How does this second problem involving 20 flags and 12 poles still differ from the classical partition problem  if “4” refers to flags, now arrangement is no longer relevant?
if “4” refers to flags, now arrangement is no longer relevant?
The 20 flags are still all different, but not in . To get even closer to the classical partition problem, let the 20 flags be all the same. How close is this? Close but not the same. For example, one partition by the classical partition problem not covered is as follows: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1. This partition into 20 portions is not possible because there are only 12 poles. What can be solved at this time, apparently, is the number of partitions of 20 flags into 12 portions. But the need is for the number of partitions in 12 portions or less. As far as I know, there is no solution to this problem.
. To get even closer to the classical partition problem, let the 20 flags be all the same. How close is this? Close but not the same. For example, one partition by the classical partition problem not covered is as follows: 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1. This partition into 20 portions is not possible because there are only 12 poles. What can be solved at this time, apparently, is the number of partitions of 20 flags into 12 portions. But the need is for the number of partitions in 12 portions or less. As far as I know, there is no solution to this problem.
By order, I evidently do not mean order in the sense of arrangement of the flags. After all, it is not possible to place the flags in different arrangements in the second problem of flags and poles because they are all identical. What is meant by order is the order of the quantities, in the sense that 1 + 3, or 1 flag on a first pole and 3 on a second, is different from 3 + 1, or 3 flags on the first pole and 1 on the second.
Much more could be said about partition. The afore-going remarks are meant to provide general background.
16.2. Partition and the Primes
Partition theory as a branch of number theory was a preferred subject of study of the celebrated, and slightly enigmatic, mathematician S. Ramanujan (1887-1920). Before him, L. Euler’s contributions to the subject were foundational.
I am not sure whether S. Ramanujan ever associated partition with primes or was ever inspired to study partition because of primes. I have not engaged in any in-depth investigations.
Advances keep being made in the theory of partition, even in most recent time. New results obtained by J. H. Bruin and K. Ono were recently widely publicized.
Partition is not an easy subject, especially when order is not important. The subject swiftly moves into higher mathematics as soon as—beyond the basic definition—past results need to be discussed when order is not relevant. Thus, in a 763-page introduction to number theory, partition is only mentioned briefly in a historical account of S. Ramanujan’s life [31] .
How is partition possibly relevant to the study of the prime sequence?
Mathematics is ultimately a reflection of how the brain perceives reality. It is customary to define primes and non-primes in terms of their factors. The focus is on multiplication. But as has been already noted in Section 11, multiplication is just an abbreviation of addition, as follows:

is nothing other than
 (23)
(23)
or
 . (24)
. (24)
In the abbreviation, information is lost in that the distinction between (23) and (24) is obliterated.
It is in regard to addition that there is a more direct way in which primes and non-primes make a statement about reality and directly affect certain very practical aspects of daily life.
Consider a number of people needing to divide into equal groups. A prime number of people cannot divide into a number of all equal large groups. A non-prime or composite number of people can.
The need to divide something into equal groups may be of concern in all kinds of practical situations. What if camp leaders at a summer camp are faced with 31 boys and need to divide them into equally large groups for all kind of tasks? If a soccer tournament were organized involving all the boys, it would not be possible to field teams that are all of equal size. The same with cleaning crews. And so on.
It is evident that a prime has partition sums just as much as a non-prime. Only, the sum components of a prime are never all the same.
What kind of answers might the student of the primes and the prime sequence want to expect from partition theory? The need is for a single function or a single formula or the like that could establish whether or not the integers of each of the partition sums of a certain integer are never all equal.
There is a procedure for establishing in how many partition sums of an integer all integers are unequal [32] .
For example, the number 6 has four such partition sums, as follows:
 ,
,  ,
,  , and
, and .
.
This result is somewhat close to the partition of primes into unequal sum components. But it is not nearly close enough. It is removed from the primes by at least three steps.
The first step of removal is that the procedure does not concern all partition sums of a certain integer. It singles out only those that exhibit a certain property, in this case all those whose integers are all different. The need is for a procedure allowing a statement about all partition sums of an integer.
The second step of removal is that the property of the partition sums in question does not cover all partition sums pertaining to primes. Take, for example, the prime 7. The partition sums
 and
and .
.
are not captured by the procedure at hand because two integers are identical. The procedure at hand only captures partition sums in which all integers are different. The procedure cannot, therefore, isolate the primes.
The third step of removal is as follows. Let us assume for the sake of the argument that there indeed exists— though there apparently does not—a procedure that identifies the exact number of the partition sums whose integers are not all equal, even if the integers of some other sums may be equal. This procedure would not exclude the possibility that, in some partition sums, all integers are indeed equal. How to establish that, in none of them, the partition sums relating to a certain integer contain integers that are all equal? Establishing this would make it possible to identify the integer in question as a prime.
There exists a procedure discovered by L. Euler that generates all the ways in which any number can be partitioned, with order not being taken into consideration [33] . J. H. Bruiner and K. Ono have recently discovered a finite formula for computing partition numbers. H. Rademacher had earlier discovered an exact convergent series for the partition function p(n), improving upon S. Ramanujan’s asymptotic non-convergent series.
Accordingly, if one would compare the number of all the possible partition sums with the number of the partition sums whose integers are not all equal produced by the fictional procedure mentioned above, it would be possible to establish whether the integer that is being partitioned is a prime or not. In the case of a prime, the two numbers would be the same. In other words, there would be no partition sums whose integers are sometimes all equal.
That would be a fine result. But the key point is this. This fictional manner of identifying primes would still only identify the primes a little bit in the way that the Sieve of Eratosthenes does. It is not clear whether it would say anything about the prime sequence itself.
It is proposed in the present paper that the prime sequence is not accessible to rational human intelligence. It is therefore suggested that the results that the study of the primes desires from partition theory will not be obtained by rational human intelligence in its current state.
Incidentally, as was already noted above, according to a celebrated proof by L. Euler, the number of partition sums containing all unequal integers is the same as the number of partition sums containing all uneven integers [34] .
For example, as was noted above, the integer 6 has 4 partitions sums featuring integers that are all unequal, as follows:

But the same integer also has four partition sums featuring only uneven numbers, as follows:

Is anything to be learned from all this? Inequality of the integers making up partition sums is associated with primes. The result is an interesting connection between primes and uneven numbers. Association of primes and uneven numbers has already been observed in Section 11 above. The deeper cause of this association may well remain opaque in light of absolute limitations imposed on rational human intelligence. In fact, as has also been noted above, L. Euler’s proof locates a true understanding of what is happening in the dimension of infinity.
17. Goldbach’s Conjecture and the Sequence of the Primes
The conjecture by C. Goldbach (1690-1764) holds that every number larger than 2 is the sum of two primes. It is obvious that a prime forming part of the sum in question can only be 2 in the case of 4. In the case of 4, the sum of the two primes is evidently 2 + 2. The primes making up the sum in question will therefore otherwise always be two uneven numbers.
There is reason to believe that the conjecture has a relation to the prime sequence. As it has been proposed above that rational human intelligence is incapable of explaining the prime sequence, does that make the conjecture also unexplainable?
Recently, it was announced that H. A. Helfgott proved the “weak” version of the Goldbach Conjecture, according to which all uneven or odd numbers greater than 7 are the sum of three uneven or odd primes. The proof can easily be found on the Internet.
The version of the Goldbach conjecture cited above is by contrast called the “strong” version. The strong version implies the weak version. Therefore, any proof of the strong version will automatically also be a proof of the weak version. The proof in question of the weak version is dozens of pages long and only few will be equipped to understand it.
It is difficult for the outsider to know what to do in the case of very long proofs, especially if all the people in the know cite one another.
Consider, for example, the case of Euclid’s Fifth Postulate. There have been countless efforts over the centuries to prove it. F. K. Gauss was the first mathematician to express the conviction that the Postulate cannot be proven [35] . One reads on occasion, as has already been noted above, that E. Beltrami and J. Hoüel proved the unprovability of it [36] [37] . But E. Schröder refers to opposition to a proof of this type, some of it bitter [38] . What does this mean? I have not further examined the matter. What is the outsider supposed to do if the leading experts cannot agree?
J.-L. Lagrange’s proofs may be strokes of brilliance. And yet in spite of that, outsiders have a sense that, if they take the time (when needed with a little help), they can succeed in following the proofs and verify their validity. Why has mathematics become so different since the time of J.-L. Lagrange?
Now back to the strong version of the Goldbach Conjecture. What is the connection between the Goldbach Conjecture and the prime sequence?
Consider, for example, the even number 20. All the possible ways in which 20 can be the sum of two uneven numbers, excluding 1, are as follows.
1) 3 + 17;
2) 5 + 15;
3) 7 + 13; and
4) 11 + 9.
Evidently, if 20 is the sum of two primes, the sums in question must be found among the four sums listed above. It appears that two of the four sums are sums of primes, namely 1) and 3).
But what about 22? All the possible ways in which 22 can be the sum of two uneven numbers can be obtained by adding 2 to the eight numbers in the four sums listed above. The result will be eight sums. It then needs to be verified whether any of these eight sums are sums of two primes.
But in fact, two of these eight sums can be eliminated even before adding 2 on the basis of other considerations. It makes no sense to add 2 to 5 or to 11 because the other number of the sum is not a prime. The two new resulting sums would therefore not yield a sum of two primes. That leaves six additions of 2 to be evaluated.
The additions in question are as follows: in sum 1), either 3 + 2 or 17 + 2; in sum 2), 15 + 2; in sum 3), either 7 + 2 or 13 + 2; and in sum 4), 9 + 2.
These additions of 2 pertain to Goldbach’s Conjecture in the following manner. If any of the additions—even just one—results in a prime, then Goldbach’s Conjecture remains valid. Put differently, according to Goldbach’s Conjecture, a prime must follow at least one of the six numbers 3, 7, 9, 13, 15, and 17. This is obviously the case. The resulting sums adding up to 22 are as follows:
1a) 5 + 17;
1b) 3 + 19;
2) 5 + 17;
3a) 9 + 13;
3b) 7 + 15; and
4) 11 + 11.
Three sums are sums of two primes. Sums 1a) and 2) are the same sum, which is a sum of two primes. Sums 1b) and 4) are also sums of primes.
With ever higher numbers, the primes are separated from one another by ever greater distances. But there are also increasingly more possible sums of primes.
Let us assume that the Goldbach Conjecture can be proven. Then the proof would presumably explain why a twin prime must follow at least one of the six numbers 3, 7, 9, 13, 15, and 17. Twin primes are two primes separated by just 2.
However, the distances between the primes are what makes up the prime sequence. The proof in question would therefore explain something about the prime sequence. The prime sequence is all about predicting by a single rule the next largest prime q after any prime p. But it is proposed in the present article that the sequence is organized but, in the end, unexplainable and the sequence therefore incomputable. It is not apparent, therefore, how Goldbach’s conjecture could ever be proven.
18. Euclid, the Primes, and the Prime Sequence
18.1. The Perennial Character of Euclid’s Elements
There is something mystical, as it were, about Euclid. And I am not referring to the contents of his works, which are all but mystical. I am also not referring to the stature of his Elements as perhaps the most widely used textbook of all time.
What does seem mystical is the fact that Euclid has never been proven wrong in anything. And he wrote so very long ago. How could his entire Elements have withstood the test of time for more than 2300 years without even breaking a sweat, as it were? The great mathematician S. Ramanujan produced some astonishing results. And yet, mistakes were found in his notebooks after his death.
Then again, Euclid must to a large extent have collected the results of earlier mathematicians. It is quite possible that all that was eventually included in the Elements had been submitted to repeated vetting over a longer time period, in the case of some results for generations.
In any event, the present concern is with primes. Euclid deals at great length with primes in Books VII to IX of his Elements, the books concerned with number theory. It seems evident that anyone interested in primes would be curious to verify what Euclid has to say about the matter.
Euclid demonstrates many properties of primes. These properties are the results of proven theorems. The theorems evidence that there is organization in the primes. But so there is in the non-primes, the even numbers, and the uneven numbers. The primes are not necessarily special in this regard.
The present focus is on the primes as a concept. What is the status of the concept according to Euclid? And what would Euclid have thought about the approach proposed in the present paper?
A distinction has already been mentioned above between the identity of the primes and the prime sequence. Both are discussed next.
18.2. Euclid’s Conception of the Identity of the Primes as an Axiom
It seems clear that Euclid considers the identity of the primes to be axiomatic. An axiom is something that most everyone, if not everyone, accepts without questioning or without demanding proof.
Euclid defines the prime axiomatically, that is, as a “definition” (horos). It is Definition 11 of the 22 definitions listed at the beginning of Book VII of his Elements. The manuscripts list it as Definition 12. But it is generally accepted that Definition 10 found in all the manuscripts is interpolated.
Definition 11 is as follows:
A prime number is any (number) measured only by a unit (that is, 1) (prōtos arithmos estin ho monadi monēi metroumenos).
The Greek can be found in J. (Johannes) L. Heiberg’s edition of the Elements [39] and E. S. Stamatis’s updated reedition of J. L. Heiberg’s edition [40] .
It is a fact that the prime is nowadays defined as a number that is divided only by 1 and by itself. But Euclid imagines divisibility as a smaller line fitting into a larger line an exact number of times. In this conception, what is the point of measuring a line by itself? What is more, if one did, the result would be 1. And Euclid does not consider 1 to be a number. He defines it as the “unit” (monas).
In terms of identity, it is difficult to see how the notion that 11 and 13 are primes requires any proof. The fact seems so obvious.
There seems to be no reason to treat very large primes any differently from small primes. That would be inconsistent.
It is true that very large primes may be difficult to find. But, as has already been noted above, that is another matter having to do with the limitations of human intelligence or of computing power. Once a new higher prime is found, there is no need for proof to accept that it is a prime. The method of finding a high prime is a computation and not a proof.
The difference between computation and proof may further be illustrated by two examples.
The first example concerns the converse of identifying a number as a prime, identifying a number as a non- prime. Both are part of the same larger problem and involve similar methods.
Thus, in early modern times, it cannot have been easy to establish that 10,072,531,043 is the product of the twin primes 100,361 and 100,363. But once the computation had been achieved, there is no need for proof that 10,072,531,043 is the product of the twin primes. All one needs to do is to simply multiply the twin primes. This procedure is computation, not proof.
To an imagined intelligence sufficiently large, it would be just as easy to observe that 10,072,531,043 is the product of the twin primes 100,361 and 100,363 as it is to observe that 15 is the product of the twin primes 3 and 15. There would be no need for computation. Computation is just a symptom of the limitations of human intelligence or computer intelligence.
The second example concerns multiplying in one’s head. Everyone will find it easy to compute in one’s head that 3 multiplied by 5 is 15. Conversely, everyone will find it easy to establish that 3 and 5 are factors of 15. But most will find it difficult or impossible to multiply 123,456,789 by 123,456,789 in the same manner. The result is 15,241,578,750,190,521. There are computing techniques to obtain the result. But that does not mean that one has proven that 15,241,578,750,190,521 is the product of 123,456,789 and 123,456,789. Computation is not the same as proof.
18.3. Euclid and the Prime Sequence
It has been proposed above that the identity of the primes is an axiom and that Euclid apparently thought so too. But what about Euclid and the prime sequence?
I could not find anything about the prime sequence in Euclid. Much of what Euclid does is establishing ratios or proportions between types of numbers regardless of what the numbers are. Euclid never mentions specific magnitudes as expressed by natural numbers such as 2, 5, 8, 12, 17, and so on.
Euclid’s propositions are all of the type that may be exemplified by Proposition 6 in Book VII, as follows:
If a number be parts of a number, and another be the same parts of another, the sum will also be the same parts of the sum that one is of the one.
It does not matter what the natural numbers specifically are. The proposition concerns a single relation that applies between infinitely many numbers.
In that regard, a matter that might have attracted the attention of Euclid—judging by the way in which he does number theory—is the sequence of all the ratios of two successive primes. This sequence looks as follows:
 ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  ,
,  , and so on.
, and so on.
It would somehow seem natural for Euclid as a number theorist to ponder whether these ratios can all be related to one another according to a single principle. There is not a single reference to the sequence in question in Euclid’s Elements. Is it permitted to speculate that the sequence did catch Euclid’s attention but that he was unable to detect any organized behavior in the sequence? There is no way of knowing.
It is proposed in the present paper that the sequence in question is indeed organized, but also that this organization is beyond human cognition. Could one have expected Euclid to consider a proposal of this nature? I believe not. Why?
The proposal made in the present paper involves infinite series. Euclid had no notion of infinite series. In recent centuries, infinite series have produced many amazing if not startling results. Then again, in infinite series, mathematical events occur in the dimension of infinity. There is therefore something fundamentally elusive about infinite series, something intangible to human cognition. On some occasions, infinite series have even been viewed with suspicion by mathematicians.
Euclid seems to offer no help in terms of the prime sequence. Did he consider the sequence to be an axiom, something that one accepts without any proof whatsoever? He does not say. And there is in the end no way to know for sure.
There is some temptation to assume that Euclid accepted that the prime sequence is an axiom, something so obvious to all that there is no need to prove it. And I admit that I was myself tempted to take this position in the course of the earlier stages of the present investigation.
A main consideration in deeming the sequence to be an axiom is as follows. Understanding the sequence includes understanding why 13 is the next largest prime after 11, the difference being 2, and 17 the next largest after 13, the difference being 4.
It seems somehow obvious why this is the case. Why would anyone want proof? The question arises: Can one then not accept the prime sequence simply as an axiom and abandon all effort at explaining it?
Again, I was certainly tempted at some point to defend such a position. Then again, what is lost in holding out hope that the prime sequence will some day be solved? It would seem as if the following is the default position typically held by mathematicians: inability to explain the prime sequence without abandoning hope that it might some day be explained.
It is against this typically held default view that the present paper takes position. It is proposed that the prime sequence is demonstrably not random and at the same time ultimately unexplainable.
I summarize some of what came before.
The contrast between what seems to be the default view and the view proposed in the present paper is therefore sharp. It also dual in nature, in relation to two On-or-Off toggles as it were.
According to the default view, the prime sequence appears random but it is not excluded that it might ultimately be explainable. According to the view in the present paper, the prime sequence appears highly organized but it is excluded that it can be understood by the human brain. The two views are exactly opposite in these two regards.
According to the default view, there may be a pattern and it may be understood. According to the present view, there definitely is a pattern but it cannot be understood.
The approach taken in the present paper also involves a call to abandoning the search for a pattern in the prime sequence. But the reason is not that the pattern cannot be found, but rather that the pattern has been found. But there is no point in trying to understand it because it transcends human cognition.
How does the present paper defend its position? It does so with what may be called empirical observations. There are two main observations. The first observation is of the pattern itself. The second observation is that the pattern involves infinity and π and therefore transcends cognition. Each will need to decide for oneself whether they can observe what I believe can be observed.
These observations cannot be called proof in the strict mathematical sense. There is no QED. The observations involve a new way of looking at the prime sequence.
18.4. Non-Primes as Hypereven Numbers and Primes as Hyperuneven Numbers
Definitions 6 and 7 at the beginning of Book VII of Euclid’s Elements are as follows [42] .
6. An even number is that which is divisible into two equal parts.
7. An odd number is that which is not divisible into two equal parts, or that which differs by a unit from an even number.
Consider the non-prime 12 and the prime 11. The non-prime 12 can be represented by dots as follows:

There are as many groups of dots to the left as there are single dots to the right. Such an arrangement is always possible when a number is a non-prime.
This arrangement is similar to the division of an even number into two equal parts. Take the even number 6. It can be represented as two equal parts by the following arrangement of dots:

This arrangement by dots is the same as the arrangement by dots of the non-prime 12 if one takes each of the three dots to the left as representative of a group of dots. If a dot can stand for a group of dots, then each unit to the left corresponds to a unit to the right in the representations by dots of both 12 and 6 above.
If a dot can stand for a group of dots in the case of the non-primes, then the non-primes share with the even numbers Euclid’s Definition 6 cited above. Non-primes might therefore be called hypereven, as it were.
By contrast, primes share with uneven numbers that they cannot be divided into two equal groups if groups of dots can be viewed as units in the case of primes. Take the prime 19. It can be represented as follows:

Then take the uneven number 9. It can be represented as follows:

If a dot can stand for a group of dots in the case of primes, then primes share with uneven numbers Euclid’s Definition 7 cited above. They cannot be divided into two equal groups and they are always a unit away from an even number, which is also a non-prime. Non-primes might therefore be called hyperuneven, as it were.
Can one think of a group of dots as a unit? Euclid defines the unit as follows in Definition 1 at the beginning of Book VII of his Elements [41] :
A unit is that by which each of the things that exist is called one.
Th. L. Heath notes in his comments to this definition of the “unit” (monas), that is, 1 of modern mathematics, that Iamblichus, who lived around 300 C.E., that the “newer” writers define the unit in this way in that it lacks the words “even if it is composite (kan sustēmatikon ēi)” [42] . I refer to Th. L. Heath’s account for all references.
In the horizontal dimension alone, the groups of dots to the left in the representation above by dots of the non- prime 12 fit exactly onto the single dots to the right, just as much as the single dots to the left in the representation above by dots of the even number 6 do onto the single dots to the right.
One is reminded of “Common Notion” 4 found at the beginning of Book I of Euclid’s Elements, as follows [43] :
Things which coincide with one another are equal to one another.
The Greek verb translated here by “coincide” is epharmozein.
What can be learned from the concepts hypereven and hyperuneven in the spatial sense? Two things.
First, it was already noted in Section 11 that certain facts of the mathematical structure of integers are such that the primes are associated for some reason with uneven numbers and that non-primes are associated somehow with even numbers, arithmetically speaking. The properties presented above in this section confirm these two associations.
Second, the associations in a sense confirm the axiomatic character of the identity of the primes. Primes exhibit the same property as the uneven numbers. No one has ever deemed it necessary to accept the uneven numbers as anything other than axiomatic. Then why would the primes be different if they behave in the same way?
19. Euclid’s Fifth Postulate and the Sequence of the Primes
19.1. The Postulate and the Sequence: Both Inaccessible to Human Cognition
What does Euclid’s Fifth Postulate do in a paper on the prime sequence? The reason is the fact that, as mathematical problems, both the Postulate and the sequence have over the centuries resisted countless attempts at deeper understanding. In this sense, they have similar status in mathematics. A comparison may therefore be useful.
It appears that they share a remarkable property in that their deeper structures are ultimately inaccessible to human cognition because these structures play out in the dimension of infinity.
As regards Euclid’s Fifth Postulate, the attempts in question have come in the form of efforts to prove the Postulate, many of them by some of the most prominent mathematicians of all time. These efforts have not been successful in the least.
As regards the prime sequence, the attempts in question have come in the form of efforts to find a formula that accounts for the distances between all the primes. Hundreds if not thousands of attempts were made, again by some of the most prominent mathematicians of all time. These efforts have not been successful in the least.
There is, however, a crucial difference between the Fifth Postulate and the prime sequence in regard to these attempts.
The attempts pertaining to the Fifth Postulate have come to an end in the nineteenth century when most everyone, if not everyone, came to agree that the Postulate is indeed unprovable. Accordingly, Th. L. Heath’s survey of efforts to prove the Postulate beginning all the way back in antiquity is not obsolete even though it was written in the early twentieth century [44] .
By contrast, the desire to find a formula for the prime sequence still persists. Then again, no one has ever even come anywhere close to establishing what such a formula might look like. In that regard, there is little or no meat to any of the pertinent efforts. It all seems more like wishful thinking.
In this regard, the following lesson may be learned for the prime sequence from the history of the study of the Fifth Postulate. It has been very difficult to convince everyone that attempting to prove the Postulate is futile. It may therefore be even more difficult to convince everyone that attempting to find a formula for the prime sequence is also futile, as is proposed in the present paper.
But there is a second way in which a comparison of the prime sequence and the Fifth Postulate seems useful. It is discussed next.
19.2. The Fifth Postulate and the Prime Sequence: Both Playing out in the Dimension of Infinity
As was noted before, it has been reported that E. Beltrami and J. Hoüel proved the unprovability of the Postulate [36] [37] . But the proof appears to be controversial [38] .
In any event, whether the proof in question is valid or not, the present concern is with another property of the Fifth Postulate that it and the prime sequence share as objects of rational human intelligence.
It has been noted above that the prime sequence transcends human comprehension because organized behavior takes place in the dimension of infinity, which is inaccessible to rational human intelligence.
It so happens that it is also possible to interpret behavior relating to the Fifth Postulate as occurring in the dimension of infinity. Accordingly, there is something that clearly transcends human comprehension with regard to the Fifth Postulate.
This behavior would in its own right seem to support the unprovability of the Fifth Postulate. How can something that is not accessible to rational human intelligence be proven?
What is the property in question? In fact, what is Euclid’s Fifth Postulate? Euclid’s formulation is as follows [45] :
That, if a straight line falling on two straight lines make the interior angles on the same side less than two right angles, the two straight lines, if produced indefinitely, meet on that side on which are the angles less than the two right angles.
What does this mean? Consider Figure 1 at the bottom of the page.
A straight line a cuts another straight line c, creating four angles 1, 2, 5, and 6. Another straight line b also cuts the straight line c, creating four additional angles 3, 4, 7, and 8. The angles 2, 3, 6, and 7 are located between the two straight lines a and b. They are therefore called the interior angles. The angles 1, 4, 5, and 8 are not located between the two straight lines a and b. They are therefore called the exterior angles.
Let it be assumed that angles 2 and 3 are together smaller than two right triangles. According to standard Euclidean geometry, the correlate is that angles 6 and 7 are together greater than two right triangles.
Euclid’s Fifth Postulate states that the two lines a and b will meet on the side of c where the interior angles are together smaller than two right angles. That side is evidently the side where the angles 2 and 3 are.
Incidentally, it is not fully clear how Euclid was led to this observation. One view that I have not found represented anywhere is that the Postulate implies that it is possible to draw a triangle. The Fifth Postulate is part of a group of five postulates of which at least the first three and possibly also the fourth state without proof that

Figure 1. Visualizing Euclid’s Fifth Postulate.
it is possible to draw a certain figure. The four others are as follows [46] :
1) To draw a straight line from any point to any point.
2) To produce a finite straight line continuously in a straight line.
3) To describe a circle with any centre and distance.
4) That all right angles are equal to one another.
How does one draw a triangle? Presumably, one draws a finite straight line AB. Next, at points A and B, one begins two straight lines whose two angles with AB are together less than two right angles or 180 degrees. According to the Fifth Postulate, the two straight lines will meet and a triangle will be formed.
An argument in favor of this view is Euclid’s variant description of the Fifth Postulate in Propositions 29 and 44 of Book I, as follows [47] :
Straight lines produced indefinitely from angles less than two right angles meet.
This is not about two lines a and b cutting a third line c, as in Figure 1 above. It is about two straight lines departing from the extremities of a finite straight line, as in drawing a triangle.
Whatever may be of the origin of the Fifth Postulate, what does the Postulate have in common with the prime sequence? It was anticipated above that both involve the dimension of infinity and are therefore inaccessible to rational human intelligence. The prime sequence is highly organized. But this organization involves infinity.
How can the Fifth Postulate be seen as involving infinity and therefore in the end being inaccessible to rational human intelligence? Consider Figure 2 at the bottom of the page.
The triangle ABC is formed by three straight lines a, b, and c. Let us assume that angle 1 is a right angle, though this assumption is not necessary. But assuming a right triangle may make it easier to visualize my argument.
Angle 2 is smaller than a right angle. Angles 1 and 2 are therefore together smaller than two right angles. According to the Fifth Postulate, a and b therefore meet on that side of c on which the two angles 1 and 2 are located.
Now let the straight line a be raised in continuous fashion so that it approaches the straight line d ever more closely. This means that angle 2 gradually increases and that angle 3 gradually decreases. It also means that the straight line a cuts the straight line b at an ever higher point, as it were.
Now let angle 3 be decreased in the following organized fashion. In the first diminution, angle 3 gradually shrinks to half its size. This also means that the point at which a and b intersect gradually moves higher up. What is more, in every subsequent diminution, angle 3 is likewise gradually reduced by half and the point of intersection of a and b keeps rising higher.
At this point, the concept of infinity enters into the picture. The following observation seems self-evident. It is possible to keep halving angle 3 without end. Accordingly, the point of intersection of a and b keeps rising without end.
There is no way in which rational human intelligence can replicate a process that never stops. How could rational human intelligence participate in a procedure that lasts forever? Everything about the human condition is finite. It is otherwise easy for human intelligence to accept that halving an angle can be carried on without end. How else could it be? Has anyone ever found a reason why the process needs to end? I believe not. Then again, truly comprehending what happens in the dimension of infinity transcends human cognition. It is time for rational human intelligence to recognize where its absolute limits are.
A similar process of continuous halving characterizes the following infinite series:

Figure 2. Euclid’s Fifth Postulate and Infinity.
 .
.
Everyone appears to accept that this sum equals 2. There is every indication that this is the case. For example, if the original infinite sum is equated with x, then 2x is as follows:
 .
.
The result of subtracting x from 2x is evidently 2. QED.
Keeping adding half of 1 to 1 and half of half of 1 to the result and so on will yield 2 as the result. But here is the catch. One needs to be able to protract the addition into infinity to get to 2. In other words, one needs to keep adding forever to get to 2. How can the human brain keep adding forever without ever stopping? And yet, this is exactly what the infinite series conveys. If one could keep adding forever, one would get to 2. Evidently, what happens in the dimension of infinity is opaque to human cognition. It is therefore not possible for the human brain to comprehend on a deeper level how an infinite sum produces a precise number.
Does this mean that, in continuously halving angle 3 in Figure 2, the end result will be that 2 becomes a right angle and a will come to coincide with d and no longer cut b? Yes, it does. But again, one cannot ever stop halving. One has to do it forever to obtain a right angle. If one never stops, one will get there. There is no doubt about it.
The three interior angles of a triangle equal two right angles or 180 degrees, as Proposition 32 of Book I of Euclid’s Elements demonstrates. Therefore, however small angle 3 becomes, one should always be able to compute the size of angle 4, however small it becomes.
Does this prove the Fifth Postulate? It does not. First of all, when angles 3 and 4 become very small, the two lines a and b may meet somewhere in outer space where no one can actually verify that they meet. And second, the process of halving the angles can go one forever. One can always add a zero after the period and make the angle smaller. But it is not possible to prove something that happens in the dimension of infinity.
All this leads to the following remarkable conundrum involving the relation between two facts that seem clear.
First, one can keep halving angle 3 into all infinity. Second, the angle must somehow become zero in the dimension of infinity. But when it does become zero, the halving must stop in infinity. In other words, in the dimension of infinity, the halving not only goes on forever but also stops. The fact is undeniable. But there is no way of understanding it.
Once again, the best approach of the human brain to this conundrum is to identify a limit beyond which its powers cannot go. Once this limit has been safely established, nothing prevents the brain from engaging in pure speculation on what may lie beyond the limit.
The same conundrum applies to the infinite series
 .
.
First, one can keep adding ever smaller fractions forever without ever stopping. But second, one will also reach 2 in the dimension of infinity. It is remarkable how self-evident these observations are. But what does it mean to end at 2 without ever stopping adding? Again, infinity transcends human cognition.
19.3. The Pesky Concept of the Infinitesimally Small
There has been so much discussion over the centuries about limits and the infinitesimally small in relation to functions and the calculus.
And there has been much dissatisfaction because the infinitesimally small seems not precise or the like. I am not sure that this dissatisfaction is founded. Nothing could be more precise or clearer than the infinitesimally small and its relation to the concept of the limit.
Consider the function
 .
.
Evidently, the larger x becomes, the smaller  becomes, as evidenced by the following sequence:
becomes, as evidenced by the following sequence:
 and so on.
and so on.
It also becomes clear that  ever more closely approaches 0 as x becomes ever larger. In other words, the difference between
ever more closely approaches 0 as x becomes ever larger. In other words, the difference between  and 0 gradually becomes what is called infinitesimally small.
and 0 gradually becomes what is called infinitesimally small.
Linguistically speaking, “infinitesimally small” means something like “becoming smaller without end”. This perception is conventionally represented as follows:
 .
.
Put into words, this Equation states that, as x keeps becoming ever larger,  will at some point become equal to 0. 0 is the limit of the gradual decrease of
will at some point become equal to 0. 0 is the limit of the gradual decrease of  in the sense that
in the sense that  cannot get any smaller than 0.
cannot get any smaller than 0.
It is easy to spot some kind of uneasy contradiction between 1) and 2). On the hand, according to 1),
 keeps getting smaller. On the other hand, according to 2), it becomes 0 and thus stops becoming smaller.
keeps getting smaller. On the other hand, according to 2), it becomes 0 and thus stops becoming smaller.
How can something keep getting smaller and stop becoming smaller? This seeming contradiction may have much to do with a certain malaise that has always surrounded the notion of the infinitesimally small.
In short, how can one make  into 0 while always keeping making
into 0 while always keeping making  smaller? The answer is obvious.
smaller? The answer is obvious.
One must never ever stop making it smaller. If one goes on forever, then one will get to 0. That is in a sense what the expression

states.  signifies a movement to infinity. But that is the same as saying that one never stops.
signifies a movement to infinity. But that is the same as saying that one never stops.
In sum, what is needed to get to 0 is to never stop making  smaller.
smaller.
The part that makes sense to the human brain is not stopping and keeping going on. What is so difficult to understand about just going on? If you do not want to stop, don’t stop. Just keep going.
The part that cannot quite be grasped by human intelligence is, not the keeping going on or the not stopping, but the going on forever or never stopping.
Not stopping is something that human intelligence can come to terms with. But what about never stopping or always keeping going on? What exactly is that like? Nothing in what the brain does or in human activity in general plays out in the dimension of infinity. In human existence, everything comes to an end. Consequently, the brain can contemplate infinity. But it cannot truly grasp it. It is something that it does not have any direct experience of.
As regards the dimension of infinity, is there something contradictory between never stopping and ending up at 0? After all, one might ask: Does one not finally stop when one reaches 0? And if one does indeed finally stop, then how can one possibly go on forever?
The answer is again clear. One stops only after one has gone on forever. What could be more obvious? The answer naturally follows from all that infinity entails. It is clear that one has to go on forever. That is what infinity is all about. It is also clear that one does end up at 0 after having gone on forever. It is also more than obvious that one cannot go on after reaching 0. Therefore, reaching 0 must come at the end of going on forever.
That much is clear to the brain. However, that does not mean that the brain has the cognitive capacity to follow a process into all infinity, just as it is able to follow, say, a soccer game or a motion picture. There is therefore something profoundly elusive to the brain about the concept of stopping after going on forever.
Everything points to the following as a mathematical fact: one goes on forever and thus reaches 0. All manner of indications demonstrate the fact. Where human intelligence hooks off, as it were, is at the point of needing to comprehend the infinite dimension of the fact.
Concepts such as “infinitesimally small” and “limit” are best defined in terms of rational human intelligence. The aim is to distinguish as carefully as possible between what is accessible to the brain and what is not, as illustrated above by the distinction between not stopping and never stopping. But back to Euclid.
19.4. The Fifth Postulate as a Transparent Concept
What the above consideration of the ever decreasing sizes of angles 3 and 4 in Figure 2 above does, I hope, is to make the Fifth Postulate more transparent. What could be more evident than that the lines a and b will keep meeting into all infinity, even if there is no proof? Axioms are after all notions that are so self-evident that most everyone accepts them without proof.
All the countless attempts at proving the Postulate suggest that the Fifth Postulate is perhaps not as immediately obvious as one might desire from an axiom.
The above considerations are designed to make the Fifth Postulate more transparent, as one would expect an axiom to be. But what is more, they are also designed to show that it is ultimately not possible to prove the postulate.
Euclid’s Fifth Postulate transcends human cognition. And what transcends human cognition cannot be proven.
Who will deny that rational human intelligence comes with limitations? The task at hand is therefore to establish where these limitations are located. There has been a tendency in mathematics to assume that the powers of the human brain are infinite and that the brain can escape its physical bonds and comprehend something that is beyond its capacity.
The halving of numerical quantities or of geometrical angles reminds one of one of Zeno’s paradoxes. According to this paradox, if one shoots an arrow at a wall, the arrow will never reach the wall. For to reach the wall, it has to first traverse half of the distance, and then half of the distance that remains, and so on. In fact, if that is what the arrow does, it will indeed not reach the wall in the finite dimensions of the human condition. But that is not what the arrow does. Then what does the arrow do? And how does the scenario of continuous halving of its trajectory to the wall described in Zeno’s Paradox relate to what it actually does? I would hope to elaborate on the matter elsewhere.
In conclusion, the design of the reflections offered in this section is not to transcend certain conundrums. That is not possible. The design is to gain a better appreciation of the absolute limitations of the human condition.
20. Excursus: The Origin of Wilson’s Theorem
20.1. Wilson’s Theorem, Its Converse, and Euclid
In the margin of the present investigation pertaining to primes, Wilson’s Theorem came to my attention. It is a well-known theorem. J.-L. Lagrange calls it a “very beautiful (très-[sic]beau)” theorem [48] . But it seems right to ask: To whom is this beauty owed?
J. Wilson proposed the theorem without proof, as did G. W. Leibniz before him in unpublished papers. But if the observation in Wilson’s Theorem was arrived at without proof, it must have been inspired by at least something. It appears that that something is in all probability Euclid’s Elements and one of its most celebrated proofs.
In a sense, on the path to Wilson’s Theorem, much of the ground appears to have been covered by Euclid. A fair share of the “beauty” of the Theorem is therefore owed to Euclid.
Then it is only fair to ask: Why did not Euclid himself come upon Wilson’s Theorem? The reason appears to be the geometrical manner in which Euclid does number theory. The Theorem involves factorials, signified by the symbol “!”, and factorials are not easy to manage in Euclid’s frame of reference if at all.
Wilson’s Theorem surfaced in the following fashion.
In 1770, E. Waring published a theorem concerning the primes that had been communicated to him, though without proof, by the English mathematician J. Wilson (1741-1793).
J.-L. Lagrange (1736-1813) took note of it and soon proposed the first proof of the theorem, and also of its converse, in a lecture read at the Paris Academy on 13 June 1771. There have been other proofs of both since then.
J.-L. Lagrange’s corresponding written paper was published in the memoirs of the Berlin Academy for the year 1771. I have used the reedition of the paper in his collected works [49] .
Wilson’s Theorem, as it came to be called, is evidently very well known. It is as follows:
If n is prime, then n divides, or is a factor of,
 . (51)
. (51)
Expression (51) can obviously also be expressed as follows:
If n is prime, then
 .
.
The symbol | stand for “divides”.
Examples are as follows. If n is 5, a prime, then expression (51) becomes
 ,
,
of which 5 is evidently a factor.
If n is 7, another prime, then expression (51) becomes
 ,
,
of which 7 is evidently a factor.
But if n is 6, a non-prime, then expression (51) becomes
 ,
,
of which 6 is evidently not a factor.
And so on.
Factorials increase in size rather rapidly. As has often been noted, this rapid increase renders Wilson’s Theorem just about useless for finding ever higher primes.
For example, if n is 19, a prime, then expression (51) becomes
18! + 1 or 6,402,373,705,728,001,
which—divided by 19—yields
336,967,037,143,579.
The converse of Wilson’s Theorem is also true. There is no report of J. Wilson himself stating it. The converse is as follows:
If n divides, or is a factor of,  , then n is always a prime.
, then n is always a prime.
20.2. Wilson’s Theorem and Euclid’s Proof of the Infinitude of the Primes
J. Wilson was a very good mathematician. He was Senior Wrangler at Cambridge University. The Senior Wrangler is the student with the highest score on the yearly mathematical tripos, a competitive exam. However, J. Wilson later led a life outside academia. No other significant mathematical result is attributed to J. Wilson.
It appears that G. W. Leibniz (1646-1716) had come upon the theorem before J. Wilson. It was found in his unpublished papers after his death [50] . But there is again no proof.
Incidentally, in his history of number theory, the most detailed to date, L. E. Dickson mentions G. W. Leibniz and J.-L. Lagrange in connection with the theorem, but not J. Wilson himself.
What strikes one about Wilson’s Theorem and about the way in which it emerged is a certain seeming isolation. I have not readily been able to find any reports regarding the circumstances in which the theorem was observed. Surely, G. W. Leibniz and J. Wilson cannot have arrived at the theorem out of the blue, as it were.
In other words, something must have led them to think at the same time about
1) primes,
2) adding 1 to a product, and
3) testing the sum of the product plus 1 for divisibility.
It so happens that I am almost certain what brought G. W. Leibniz and especially J. Wilson to Wilson’s Theorem. I cannot positively prove it. A much more detailed investigation remains desirable.
The mathematical tripos at Cambridge University is not about producing new results in mathematics. It is about applying known rules with speed and accuracy. The question arises: What did the mathematical knowledge that J. Wilson acquired at Cambridge University include?
Surely, Euclid’s Elements must have occupied a prominent place in his education. It is perhaps the most popular textbook of all time. And studying many if not most or all of Euclid’s many, many theorems must have been part of a good preparation for the mathematical tripos.
Among Euclid’s theorems is the proof that there are an infinite number of primes in Proposition 20 of Book IX of the Elements. Euclid does not quite say that there are infinitely many primes. Rather, he puts it is as follows: if one has a certain number of primes, one can always add another one. The matter is detailed further below.
I cannot fail to notice the similarity between how Euclid understands infinity and the way in which I would prefer to understand it myself, as described in Section 15 above, namely as follows: One can always add 1. What could be more obvious? Once again, no one has ever bet against Euclid and won.
It appears that Euclid’s proof exhibits the following three characteristics identified above as being also characteristics of Wilson’s Theorem:
1) a concern with primes;
2) adding 1 to a product; and
3) testing the resulting total sum of the product plus 1 for divisibility by factors.
Euclid’s proof in question is in more popular treatments of mathematics considered to be one of the most elegant of all time. It therefore comes as a bit of a surprise that it is typically misrepresented in standard accounts of number theory (see below). The proof that is often styled as Euclid’s does indeed prove the infinitude of the primes. But it is not quite Euclid’s. It is a special case of Euclid’s. Apparently, hardly anyone ever bothers to go back to the original text of Euclid’s proof.
As was said before, the study of Euclid’s proof that there are an infinite number of primes can easily lead to the observation of Wilson’s Theorem. It almost seems as if the Theorem is just there for the taking.
Did J. Wilson, and perhaps also earlier G. W. Leibniz, stumble upon Wilson’s Theorem through Euclid’s celebrated proof that the primes are infinite? I strongly suspect so. How else could it have been?
In any event, the following is an undeniable fact. I myself stumbled upon a proof of the converse of Wilson’s Theorem while studying Euclid’s proof. I cannot quite reconstruct the train of thought that led me from Euclid’s proof to a proof of the converse of Wilson’s Theorem. In any event, I have not found this manner of proving the converse reported anywhere.
Naturally, the contemplation of the converse of Wilson’s Theorem, whether proven or not, easily leads to the contemplation of the Theorem itself (see below).
Were J. Wilson or G. W. Leibniz aware in any way of the converse without reporting this awareness and did they come to Wilson’s Theorem by way of the converse?
The question arises: Why did Euclid himself not present a proof of either Wilson’s Theorem or its converse? The answer is not, and cannot be, that Euclid simply missed it. Rather, the answer lies in how Euclid does number theory (see above and below). According to his manner of doing number theory, it seems very unlikely that he could have found a proof of the converse of Wilson’s Theorem.
Before presenting the proof of the converse in question, it will be useful to describe Euclid’s proof of the infinitude of the primes.
20.3. Arithmetical Description of Euclid’s Proof of the Infinitude of the Primes
In the interest of clarity, though not necessarily of brevity, I will not describe the proof in Euclid’s own geometrical fashion, and not even in algebraic fashion as is often done, but rather in simple arithmetical fashion.
I somehow feel that number theory could be made much more inviting if proofs were presented in this fashion. Then again, understanding Euclid on his own terms remains always enlightening in its own right.
Euclid wants to show that, if one has a group of primes, one can always find one more, into all infinity. He proceeds as follows.
Consider the following two simple groups of primes:
1) 2 and 3;
2) 3 and 5.
Next, one considers the product of these groups and adds 1. The results are as follows:
1) ;
;
2) .
.
The need is for an extra prime. There are two cases. In the first case, the product plus 1 is a prime, as in 1). In the second case, the product is not a prime, as in 2).
In the first case, one immediately obtains the needed extra prime, 7 in this case.
In the second case, the needed prime is obtained as follows. The product of the primes in 2) above is
 .
.
Accordingly, geometrically speaking, the two primes 3 and 5 will both fit an integer number of times into 15, as follows: 3 fits five times into 15 and 5 fits three times into 15.
It follows that, if one adds 1 to 15, neither 3 nor 5 can fit an integer number of times into the sum, namely 16. In other words, neither 3 nor 5 can be factors in a product whose result is 16.
It is a fact that all non-primes are products of primes. So is the non-prime 16. Which are the primes whose product is 16? One thing is certain. Neither 3 nor 5 can be one of the sought primes. It has been noted above that both fit an integer number of times into 15. How, then, could they also fit an integer number of times into 16?
As Euclid puts it in geometrical fashion, here translated into arithmetical fashion, if 3 fits an integer number of times into both 15 and 16, then it would also need to fit an integer number of times into the difference between 15 and 16, which is just 1. Euclid calls 1 the “unit” (Greek monas) and does not consider it a number (arithmos).
Euclid asks the equivalent of the following question: How can a number like 3 be made to fit an integer number of times into 1? Again, he imagines this concept geometrically as a line of longer length fitting into a line of shorter length. He declares this concept to be “absurd” (atopos).
All this means that some prime other than 3 or 5 must be part of the product of primes whose result is 16.
In the example at hand, there is only one other prime and it is 2, since . In sum, 2 is the needed extra prime. In other words, it has been possible to prove—from the mere existence of the primes 3 and 5—that there must be one more prime.
. In sum, 2 is the needed extra prime. In other words, it has been possible to prove—from the mere existence of the primes 3 and 5—that there must be one more prime.
What is more—as Euclid points out—this process can be repeated endlessly with all kinds of primes. That is, one can always find one more prime. And this is the same as saying that the number of the primes is evidently infinite. QED.
20.4. Misrepresentations of Euclid’s Proof of the Infinitude of the Primes
An exhaustive search has not been possible, but it is difficult to find Euclid’s proof of the infinitude of the primes described correctly anywhere. I refrain from listing all the works on primes that I have checked in regard to this matter.
A principal reason for the absence of true accounts of Euclid’s proof must be that most accounts of the proof are derivative of other accounts, without the original Greek text of the proof—or a translation thereof—ever having been checked.
The proof that is styled in error as Euclid’s is otherwise valid even if it is not Euclid’s.
It would require much historical work to investigate when misrepresentations of Euclid’s proof first began showing up in the mathematical literature.
Th. L. Heath gets it right in his commentary on Euclid’s Elements [51] . But then, his commentary accompanies his own translation. Evidently, Th. L. Heath had read the proof in the original Greek.
The most common inaccurate representation involves two ingredients that one does not find in Euclid’s proof. I have found it in the handbook by G. H. Hardy and E. W. Wright [52] and in the textbook by J. E. Pommers- heim, T. K. Marks, and E. L. Flapan [53] .
The first ingredient is what one might call the prime factorial. Whereas the regular factorial (!) of a number is the product of all the successive natural numbers smaller than or equal to that number, as in
 ,
,
the prime factorial of a prime is the product of the successive primes smaller than or equal to that prime. Thus the prime factorial of 11 is
 .
.
Euclid’s geometrical manner of practicing number theory does not make the use of factorials easy. As far as I know, Euclid does not use regular factorials or prime factorials or any equivalent thereof.
The second ingredient is the search for a larger prime. By contrast, Euclid’s search is for another prime, whether smaller or larger. In that regard, the alternative proof is a special case of Euclid’s proof. In the alternative proof, the primes given at the outset form a prime factorial. In Euclid’s proof, any configuration of primes can be part of the primes given at the outset.
The title of Euclid’s proof is, in Th. L. Heath’s translation, “Prime numbers are more than any assigned multitude of prime numbers”. Has “more” on occasion been understood as “greater” by anyone who did not read the proof itself?
L. E. Dickson also assumed that Euclid’s proof involves the search for a greater prime rather than the search for more primes while referring to the edition of the original Greek, along with a Latin translation, by I. L. Heiberg. He describes the proof as follows [54] :
Euclid noted that, if p were the greatest prime, and  is the product of all the primes
is the product of all the primes , then
, then  is not divisible by one of those primes and hence has a prime factor
is not divisible by one of those primes and hence has a prime factor , thus involving a contradiction.
, thus involving a contradiction.
Euclid has no notion of what L. E. Dickson calls the “greatest prime”. Also, L. E. Dickson omits the possibility that  is itself a prime.
is itself a prime.
The proof in question, which is valid while not being Euclid’s, may be described as follows. The starting-point is any prime factorial. The aim is to show that there is a prime greater than the primes of the factorial.
Take, for example, the prime factorials of 11 and 13 augmented by 1, as follows:
 ;
;
 .
.
As in Euclid’s proof, two possibilities present themselves. Either the result is a prime or it is not a prime.
If it is a prime, then a larger prime has been immediately obtained. QED. This is the case with 1471, which is a prime.
If the result is not a prime, then it must be—like all non-primes—a product of primes. This is the case with 30,031, which is not a prime. It is therefore a product of primes.
But which primes? Clearly, none of the ones belonging to the prime factorial. If 2, 3, 5, 7, 11, and 13 fit an integer number of times into 30,030, then they surely do not do so into 30,031. The prime factors of 30,031 must therefore be larger than 13. In fact, 30,013 is the product of the two primes 59 and 509. The desired larger prime has consequently been found. QED.
20.5. A New Proof of the Converse of Wilson’s Theorem in Euclidean Fashion
It was suggested above that J. Wilson and G. W. Leibniz may have been inspired, in obtaining Wilson’s Theorem, by Euclid’s proof of the infinitude of primes. The proof shares three key properties with the Theorem, as follows:
1) a concern with primes;
2) adding 1 to a product of primes; and
3) testing the resulting product augmented by 1 for certain types of divisibility.
There is a crucial element that Wilson’s Theorem does not share with Euclid’s proof: the factorial (!).
The alternative proof described in Section 20.4 contains prime factorials. Did this proof possibly inspire J. Wilson or G. W. Leibniz to investigate regular factorials in terms of what divides them once they are augmented by 1? I have not investigated whether the alternative proof already existed in the time of J. Wilson or G. W. Leibniz. Such an investigation might involve some laborious historical research.
In any event, it is possible to prove the converse of Wilson’s Theorem along the lines of Euclid’s proof of the infinitude of the primes. I have not been able to find the proof in the mathematical literature. Two stratagems need to be used that are not found in Euclid’s proof, the following:
1) looking at primes from the perspective of the non-primes;
2) the factorial.
As was already noted above, the converse of Wilson’s Theorem is as follows:
If n divides , then n is a prime.
, then n is a prime.
I see no way of proving the converse directly in Euclidean fashion. But the correlate is another matter.
The correlate of the converse concerns the non-primes. The correlate is as follows:
If n is not a prime, then n does not divide .
.
If one can prove the correlate of the converse, then the converse itself is automatically proven as well.
The correlate can be proven as follows. I again prefer to use an exposition of the arithmetical type for easy access.
Let the non-prime n in the correlate of the converse of Wilson’s Theorem be 6. It will appear that there is no reason why the following line of argument applying to 6 does not apply to all other non-primes as well.
Accordingly, the need is for evaluating the expression

or

in terms of what divides it.
The key question is as follows: Is the expression in question divisible or not divisible by 6—or by n in general if n is a non-prime?
Because 6 is a non-prime, 6 must be a product of primes. What is the identity of the primes making up the product whose result is 6?
Evidently, the primes that are factors of 6 are smaller than 6, and that at least by half. This means that they need to be found among the components of the factorial of, 5, that is, 5! The factorial of 5 includes all the natural numbers that are smaller than 6.
The primes whose product is 6 are 2 and 3. According to the fundamental theorem of arithmetic, there is no other way to represent 6 as a product of primes; each non-prime corresponds to a unique product of primes.
It is evident that the expression

is divisible by 2, 3, 4, and 5.
At the same time, it is obvious that the expression

cannot be divisible by 2, 3, 4, or 5.
That also means that it cannot be divisible by 6 because 6 is the product of 2 and 3. QED.
The same reasoning can be applied to all the non-primes. It also follows that, if any number n divides the expression
 ,
,
it must be a prime, which is the converse of Wilson’s Theorem.
20.6. Appendix to the Excursus: Wilson’s Theorem, Lagrange’s Proof Thereof, and Pascal’s Triangle
The design of what follows is to explain a peculiar property of the numbers in Pascal’s Triangle. Though I was familiar with the Triangle, the property had not attracted my attention until I read D. Wells’s description of it [55] . D. Wells does not provide an explanation.
The explanation of the property connects with what has been said before in this paper in two ways. First, it connects with the paper in general in that it concerns primes. This paper is about primes. Second, it connects with the present excursus on Wilson’s Theorem in that the explanation of the property is of the same type as J.-L. Lagrange’s proof of Wilson’s Theorem, the first proof ever of the theorem.
The numbers of the triangle are the coefficients of the expansion of the powers of the binomial . For example, in
. For example, in
 ,
,
the four coefficients are
1, 3, 3, and 1.
In
 ,
,
the five coefficients are
1, 4, 6, 4, and 1.
The numbers are represented in the following figure, from exponent 0 to exponent 8.

and so on.
One will note that every number in the triangle is the sum of the number above it to the left and the number above it to the right.
The property in question is that, in the case of prime exponents, the exponent always divides all the corresponding numbers except 1. For example, in the third row, 3 divides 3. In the fifth row, 5 divides 5 and 10. In the seventh row, 7 divides 7, 21, and 35. And so on.
By contrast, in the case of the non-prime exponents, the exponent may or may not divide the corresponding numbers besides 1. Thus, in the fourth row, 4 divides 4 but does not divide 6. And in the eighth row, 8 divides 56 but does not divide 28. And so on.
A. F. W. Edwards has described much if not most of what is known about Pascal’s Triangle at length [56] . But there is no mention of primes in his work.
Incidentally, the broader project of which the present paper is part is rational human intelligence. The design of the broader project is to demonstrate that rational human intelligence is entirely digital. It is therefore interesting to observe the connection between Pascal’s Triangle and digitality and therefore indirectly between Pascal’s Triangle and rational human intelligence.
Consider that classic embodiment of digitality, the light-switch. For example, in how many ways and in which ways exactly can three light switches be On or Off?
The answer is provided by expanding the expression (On + Off)3 in the same way as the expression  above into
above into

The symbol “×” needs to be understood digitally as AND, not quantitatively.
Evidently, there are eight ways, that is, 23. The two center expressions denote the three ways in which only one switch is Off, namely

and the three ways in which only one switch is On, namely

The three switches are marked by the raised numbers 1, 2, and 3.
If there were four light switches, there would by 16 or 24 ways, shown in the following expansion of (On + Off)4:

This much for a light switch. But what about rational human intelligence? I refrain from treating the digitality of rational human intelligence here in any detail. Let it suffice to consider here ever so briefly the following question: How many different classes of people are there exhibiting none, some, or all of the four attributes “male”, “doctor”, “French”, and “under 40 years of age”. It appears that there are 16. That is exactly as many classes as there are ways in which four light switches can be On or Off. The coefficients 1, 4, 6, 4, and 1 also apply.
But again, this is not the place to explore the connection between Pascal’s Triangle and the structure of rational human intelligence. I hope to do so much more fully elsewhere.
The crucial question remains: What explains the behavior of prime exponents in Pascal’s Triangle in terms of divisibility?
The explanation is obvious if one considers the structure of the coefficients. Consider the coefficients of exponent 7 except the first and the last, which are both 1. They are the following: 7, 21, 35, 35, 21, and 7.
L. Euler displays how these six coefficients are obtained in his Elements, this paragon of clarity and distinction, as follows [57] :

These coefficients can also be written as follows:

It is evident why all the coefficients are divisible by 7, and by extension why they are all divisible by the exponent when the exponent is a prime.
To obtain the natural numbers that are the coefficients, factors common to numerators and denominators need to be canceled. As a prime, the number 7 in the numerator can only be canceled by itself in the denominator. But it only occurs in numerators. It is therefore never canceled. The coefficients are therefore all divisible by 7. The same reasoning applies to all the primes.
A similar inability to cancel a prime plays a crucial role in J.-L. Lagrange’s proof of Wilson’s Theorem. To repeat, Wilson’s Theorem is as follows:
If n is prime, then n divides, or is a factor of,
 . (51)
. (51)
Everything revolves around the divisibility of a number by primes.
J.-L. Lagrange proves Wilson’s Theorem by pointing out that certain natural numbers as coefficients are always divisible by a certain prime because the prime appears in the numerators but not in the denominators of fractions that, after cancellation of common factors, yield the coefficients in question.
This is not the place to analyze J.-L. Lagrange’s entire proof. He obtains the proof by manipulating coefficients. L. Euler famously manipulated coefficients to obtain interesting results in partition theory.
J.-L. Lagrange’s results in relation to Wilson’s Theorem include an interesting rule that describes by a single principle how any factorial relates to the next largest factorial, say 4! to 5!, 5! to 6!, and so on (see below).
The focus of what follows will not be on the entire proof but only on those parts thereof that evaluate coefficients in terms of divisibility by primes. I will make the description arithmetical by choosing a specific prime, namely 5. It will be easy to see that what is said below about 5 applies to any prime.
The point of departure of J.-L. Lagrange’s proof is the evaluation of the expression
 .
.
If n is the prime 5, then the expression becomes
 .
.
By multiplying out, one obtains the following expression, which includes the coefficients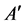 ,
,  ,
,  , and
, and :
:
 .
.
 is evidently
is evidently  or 4! It corresponds to the expression
or 4! It corresponds to the expression  that is part of Wilson’s Theorem. The Theorem revolves entirely around this expression augmented by 1, that is,
that is part of Wilson’s Theorem. The Theorem revolves entirely around this expression augmented by 1, that is,  , and its divisibility by primes.
, and its divisibility by primes.
It is clear what the coefficient  is. But what about the coefficients
is. But what about the coefficients ,
,  , and
, and ? It is expected that they are natural numbers. And it is expected that factorials will play a role in obtaining the natural numbers.
? It is expected that they are natural numbers. And it is expected that factorials will play a role in obtaining the natural numbers.
J.-L. Lagrange demonstrates the following:
 (52)
(52)
 and
and  are a kind of involuted factorial expressions, fascinating to observe.
are a kind of involuted factorial expressions, fascinating to observe.
It is clear that all three coefficients in (52) are divisible by 5 because 5 is a prime. In the fractions that yield the natural numbers as coefficients, 5 appears in numerators but not in any denominators. The number 5 can only be canceled or reduced if it has factors that also appear in denominators. But because 5 is a prime, it is only divisible by itself. And since, again, 5 does not appear in any denominators, it is never canceled. Accordingly, the natural numbers that are the coefficients always have 5 as a factor. In other words, 5 divides them. The same reasoning applies to all the primes.
Another way of representing (52) is as follows:

The results are as follows:

J.-L. Lagrange also shows that, when n is 5:
 (53)
(53)
Entering the values of the coefficients yields the following expression:

Or also
 (54)
(54)
and
 .
.
Expression (53) is evidently also equivalent to
 . (54)
. (54)
The left-hand side of this equation is an instance of the expression around which Wilson’s Theorem revolves, namely
 ,
,
with p being a prime, in this case 5.
The crux of J.-L. Lagrange’s proof is that all the components of the right-hand side of (54) are divisible by 5. And the same reasoning applies to all the primes. Accordingly, the left-hand side of (54), namely , must be too. And thus, in general,
, must be too. And thus, in general,  will always divisible by the prime p. QED.
will always divisible by the prime p. QED.
Expression (54) also provides an interesting way of relating every factorial, not only factorials of primes, to the next largest factorial, that is, relating n! to .
.
The generalized equivalent of (54) is as follows:

Or also as follows:

The numbers accompanying A are obviously not exponents. They count the number of coefficients, of which there will be . When n is 5, as was the case in the example above, one will need to reckon with 5 − 2, or 3, coefficients.
. When n is 5, as was the case in the example above, one will need to reckon with 5 − 2, or 3, coefficients.
It appears that dividing  by
by  leads to the same result as subtracting the expression
leads to the same result as subtracting the expression
 (55)
(55)
from it, namely n!. A product is associated with a sum. Expression (55) is the quantity by which any factorial is smaller than the next largest factorial.
Acknowledgements
A statement of acknowledgements is an opportunity to express gratitude for support received in the course of an endeavor—in the present case, an intellectual endeavor. The following acknowledgments may perhaps appear to readers as Something Completely Different from what one might expect in a mathematics article. Yet, they help explain the circumstances in which the present paper came into existence. The paper owes much to these circumstances.
First of all, I acknowledge the suggestions and comments by an anonymous reviewer who realized that this paper by someone who is not strictly speaking a mathematician may not be your traditional mathematics paper, yet deemed it worthy of publication.
In a paper that is intimately related to the present one in that it shares the same ultimate purpose of presenting a complete and final theory of rational human intelligence [58] , I already expressed my personal opinion that style is everything, citing G.-L. Leclerc (1707-1783), Comte de Buffon, who actually said, “The style is the man (Le style c’est l’homme même)”. And I singled out the composer G. B. Pergolesi (1710-1736) as a true inspiration.
The celebrated traveler, author, and musician Ch. Burney (1726-1814), father of the novelist Fanny Burney, described G. B. Pergolesi’s music not only as singularly clear, simple, and true, but also as sweet [59] .
In this connection, the Belgian composer A. E. M. Grétry (1741-1813), who won great acclaim at theaters and the royal court in France, who wrote the music for Voltaire’s funeral, and whose body is buried at the famed Père Lachaise cemetery in Paris while his heart rests in a shrine below a statue of him towering in front of the Royal Opera of Wallonia in his native Liège in Belgium, famously stated the following about G. B. Pergolesi in his Memoirs [60] :
Pergolesi was born and the truth was known (Pergolèze naquit et la vérité fut connue).
G. Radiciotti fittingly put this statement on the title page of the first edition of his biography of G. B. Pergolesi [61] . A street is named after A. E. M. Grétry in the center of Brussels, Belgium. And a restaurant in this street even bears the name of his memoirs.
As noted already above on more than one occasion, the present article is part of a larger project on rational human intelligence. This project is deeply influenced by the works of G. Boole (1815-1864). One design of this project is to advocate for the following conviction regarding rational human intelligence:
G. Boole was born and the truth was known (G. Boole naquit et la vérité fut connue).
It occurred to me at some point that there is an almost eerie resemblance between G. Boole’s work and G. B. Pergolesi’s work in terms of how they have fared in the decades or centuries following their deaths and then, by stark contrast, in recent decades. There is no denying that their labors have been appreciated. As for G. B. Pergolesi, he was perhaps the first composer of truly international renown. As for G. Boole, how many mathematicians have an entire algebra named after them?
Then again, how many would name G. B. Pergolesi among the five to ten greatest composers of all time? How many would name G. Boole among the five to ten greatest mathematicians of all time? Where would the two men place in a ranking of hundreds of the most prominent musicians and mathematicians respectively? And how well are they known to the wider public?
I have elsewhere described the great influence—even if a very indirect one—of J. C. Maxwell’s (1831-1879) theory of electromagnetism on the afore-mentioned larger project on rational human intelligence [62] .
It was my acquaintance with this theory and its significance that convinced me personally all at once in a watershed revelation in late 2012, 1), that the theory of rational human intelligence is a theory of physics with its own mathematics, 2), that the theory can be complete, and 3), that the theory is a so-called “black box” theory.
When it comes to the fate of J. C. Maxwell’s legacy, there is an uncanny resemblance with the fates of G. B. Pergolesi’s and G. Boole’s legacies described above. It can hardly be said that J. C. Maxwell has gone unrecognized. Very far from it. Then again, how many would name J. C. Maxwell among the top five to ten physicists of all time? A recent biographer, B. Mahon, is not a little baffled at how little—relatively speaking—J. C. Maxwell seems to be known and he adduces evidence to support the fact [63] . In this connection, he rightly notes the following about J. C. Maxwell’s influence on “the whole development of physical science” [64] :
[Maxwell] started a revolution in the way physicists look at the world. It was he who began to think that the objects and forces that we see and feel may be merely our limited perception of an underlying reality which is inaccessible to our senses but may be described mathematically.
This statement might as well describe the way of looking at the prime sequence that is advocated in the present paper. It also describes the way in which I propose to look at all of rational human intelligence.
A fourth key influence is the Italian-French J.-L. Lagrange (1736-1813), “generally regarded as the keenest mathematician of the eighteenth century” [65] . It has already been noted in Section 15 above that he writes the following in his “Analytical Mechanics (Mécanique analytique)” [66] :
The purpose of this work is to reduce mechanics to purely algebraic operations.
What J.-L. Lagrange does in this work is to derive all of mechanics from a single principle, which he describes as the principle of “virtual velocities”. I mention this here because I firmly believe that it is possible to likewise derive all of rational human intelligence from a single principle, improbable as it may sound. And I hope to present such a derivation elsewhere. Rational human intelligence is a physical mechanism. And it is time for nothing less than construing a Mécanique rationnelle (“Rational Mechanics”) in the wake of J.-L. Lagrange’s Mécanique analytique (“Analytical Mechanics”).
In this connection, an incidental remark on style as it relates to writing mathematics is in order. Why is mathematics no longer written in the style of L. Euler and J.-L. Lagrange? The desire dating to the nineteenth century for making mathematics rigorous, whatever that means, seems to have eliminated the human factor. Maybe, one unspoken design of the compact style of current mathematical writing is somehow to make mathematics look more clinical, more objective, more professional. But is it really necessary that mathematics should only be understood by mathematicians?
As is proposed in the present paper, the prime sequence exposes an absolute limitation to rational human intelligence. In general, as an empirical phenomenon, mathematics is in the end something that the human brain does. It can be directly observed and studied only as brain activity. No level or type of rigor can disembody mathematics and make it into something transcendental.
Because mathematics is believed by many to be something like the Sacred Code of the Book of Nature, there has been a desire to lift it up to something like divine status. However, it is not possible to know mathematics beyond the limitations of rational human intelligence. One should always keep the human dimension in sight.
Just as the Greek miracle took place because man—and not the gods—was for the first time taken as the measure of everything, it is time for man also to become the measure of mathematics.
In my opinion, mathematicians like G. Frege and G. Cantor and others were looking for a transcendental level in mathematics that can simply not be attained. Both suffered breakdowns and there has been some speculation as to whether they overextended themselves intellectually.
Nothing is more self-evident than that the brain comes with absolute physical limitations. How else could it be? Is there anyone out there who wants to argue that the intelligence of the brain is as large as the final secrets of the universe itself?
The following strategy therefore recommends itself: One ought to focus on locating the limits of one’s own rational human intelligence. Once the limits have been established, anything else beyond these limits is just speculation. If I tried to comprehend what is beyond my own intelligence, I would need to step outside of my own brain, as it were. And if I tried to do that, I am sure that I too would suffer a serious breakdown.
But back to J.-L. Lagrange. J.-L. Lagrange’s legacy does not seem to have suffered the same fate as G. B. Pergolesi’s, G. Boole’s, and J. C. Maxwell’s. He is buried in the Pantheon in Paris and his name is prominently visible on the Eiffel Tower in Paris on the side facing the Seine.
Still, does the name J.-L. Lagrange resonate in the same way among the wider public as Pythagoras, Euclid, Archimedes, R. Descartes, B. Pascal, I. Newton, G. W. Leibniz, J(akob) Bernoulli, J(ohann I) Bernoulli, D. Bernoulli, L. Euler, or F. K. Gauss? It should. But I am not sure that it does. It is interesting to note that J.-L. Lagrange was born in the same year in which G. B. Pergolesi died, 1736.
By the way, G. B. Pergolesi’s most ardent admirer, A. E. M. Grétry, seems to have suffered a fate even worse than the subject of his admiration. One just wonders how many patrons of the afore-mentioned restaurant “The Memoirs of Grétry” in the Grétry Street in Brussels know who A. E. M. Grétry was.
Is the large scale effort of which the present paper is part and whose aim is to achieve a clear exposition of the totality of rational human intelligence betting on all the wrong horses?
In this regard, another remarkable property characterizes and unites the personalities and the works of G. Boole, J. C. Maxwell, and G. B. Pergolesi. After long interludes of oblivion, their stars have been—relatively speaking—sharply on the rise in the last 30 to 40 years or so, accelerating rapidly especially in the 1980s and 1990s, most of the acceleration occurring after my undergraduate years and much of it even after my graduate work. This means that, when I was a student, there would have been little incentive to recognize G. Boole, J. C. Maxwell, and G. B. Pergolesi as prime paragons of Western civilization. And in fact, my own interest in their personalities and their work has been the result of chance encounters in recent years.
As regards G. Boole, there is now a study of his logic and probability (first edition: 1976; second edition: 1986) [67] [68] , an edition of his correspondence with A. De Morgan (1982) [69] , a biography (1985) [70] , an edition of his correspondence with S. Jevons (1991) [71] , an edition of unpublished manuscripts on logic and its philosophy (1997) [72] , and a Boole anthology (2000) [73] , all works published after my undergraduate years, except one by Th. Hailperin, though only in its first edition.
As regards G. B. Pergolesi, there has been a flurry of activity roughly in the same recent decades, also accelerating in the 1980s and the 1990s. This activity includes world premiers in modern times of many musical works including his seemingly forgotten operas, conferences devoted to him, a new series entitled “Pergolesi Studies/ Studi Pergolesiani”, research centers founded in New York and Milan, and a guide to research [74] , to which I refer for more detail. B. S. Brook, F. Degrada, H. Hucke, D. Monson, and M. E. Paymer have been at the forefront of the revival of Pergolesi scholarship.
It may be noted in the margin that the music by A. E. M. Grétry has also made something of a comeback. And, in general, period interpretations of baroque works have been on the rise. For half of my life, the second Brandenburg concert was almost never played on natural baroque trumpets. Now, using a natural trumpet is de rigueur.
As regards J. C. Maxwell, the James Clerk Maxwell Foundation was formed in 1977 in Edinburgh and the house in which he was born serves as its headquarters. And there is now also the afore-mentioned biography by B. Mahon.
I am still a little bemused by the fact that what has directly and indirectly inspired my efforts to describe rational human intelligence has benefited from minor paradigm shifts just in recent decades, and in my lifetime. What exactly happened? I will treat it as a good omen for the efforts in question, such as they are.
The present acknowledgments began with the mention of G. B. Pergolesi’s style and the inspiration derived from it. It then appeared that the recent revival of his work parallels a revival of G. Boole’s oeuvre and therefore becomes a musical metaphor, as it were, of a changing intellectual climate.
It will be useful to buttress these two points further, first by detailing G. B. Pergolesi’s style a little more and second by showing that the revival of his music is not a fluke in the sense that—while there have been his detractors, some ardent—many others have considered his music unsurpassed and some even unparalleled.
Four observations on style. First, “natural” is a property that I should have added to the characteristics of G. B. Pergolesi’s style already mentioned above and also elsewhere. According to A. E. M. Grétry [75] ,
The truth of declamation constituting [G. B. Pergolesi’s] songs is as indestructible as nature (la vérité de déclamation qui constitue ses chants, est indestructible comme la nature).
Second, G. B. Pergolesi is in my opinion on quite a few occasions just ever so subtly mischievous in a way that I only rarely discern in the music of other composers. It seems to mean that he does not take himself too seriously. And that is good to know.
Third, citing an eyewitness account gathered in the course of his travels in Italy, Ch. Burney describes G. B. Pergolesi as a “slow composer” [76] . His biographer G. Radiciotti interprets Ch. Burney as stating that the composer was “an accurate worker using a file ([un] lavoratore accurato e di lima)” [77] . This seems like a mis- translation improving on the original.
But the fourth characteristic has perhaps been the most inspiring in the present context. It is the way in which G. B. Pergolesi’s lines of melody (supported by an accompaniment that never takes control but impeccably does all it possibly can to enhance the melodic line) run from the very beginning to the very end without a single note being out of place, and all this with—at almost every turn—plenty of originality and unexpected and interesting twists that surprise but never either disrupt the line or displease. Originality by itself could be classified as yet a fifth characteristic.
G. B. Pergolesi’s melodic lines stand as a metaphor of how one would like an intellectual argument to proceed. Again, style is everything. D. Monson has established that the composer “wrote the music for the vocal line before writing the bass and accompaniment” [78] . In the same way, the stepwise rigorous intellectual coherence of the main line of an intellectual argument is paramount.
This much about Pergolesi’s style. But what about his reputation? I select testimonies by the great philosopher J.-J. Rousseau (1712-1778), the great mathematician and student of the physics of music, J. Le Rond D’Alembert (1717-1783), the great contemporary French composer J.-Ph. Rameau (1683-1764), and—who else—the eternal J. S. Bach (1685-1750) himself, none of them Italians by the way. There have been detractors, a number of Germans and some English. Perhaps, at some point, someone will be able to find out what to make of it all.
But before adducing the testimonies in question, a unique property of G. B. Pergolesi’s legacy may be pointed out. It appears that, of the compositions that have been attributed to him at one point or another, perhaps 80% or 90% are not by him. There is nothing anywhere close to it in the history of music.
As regards the testimonies anticipated above, J.-J. Rousseau—who himself composed respectable music— called G. B. Pergolesi “inimitable (inimitable)” [79] .
All culminates, evidently, in G. B. Pergolesi’s Stabat mater, composed just before his death. The analogy has very often been made with W. A. Mozart’s (1756-1791) Requiem, which he composed on his deathbed. Did J.-J. Rousseau exaggerate when he called the opening duet of G. B. Pergolesi’s Stabat mater “the most perfect and the most touching that has ever come from the pen of any musician”? [80]
According to J. Le Rond D’Alembert, who by the way exerted much influence on the afore-mentioned J.-L. Lagrange in matters of mathematics and physics, G. B. Pergolesi was the “Rafael of Italian music” [81] .
There was much discussion in the eighteenth century as to whether either French or Italian opera music was superior. In that regard, A. E. M. Grétry reports that J.-Ph. Rameau, this paragon of French music in the eighteenth century and the successor to the Italian-born French composer J.-B. Lully (1632-1687), confided to his friend the Reverend Arnaud when he was about 60 years old, that, if he were 30 years younger, he would travel to Italy and compose in the style of G. B. Pergolesi [82] . But he felt that he was too old for change. What about that for a confession?
And then there is J. S. Bach. To my knowledge, the only work that he copied and adapted from another composer in full orchestration, and not just in a conversion for keyboard, is G. B. Pergolesi’s Stabat mater. A fitting tribute indeed. J. S. Bach schoolishly completes harmonies, adding the fourth note. But it is a matter of taste whether the result is an improvement.
G. B. Pergolesi has been adduced above, 1), as a metaphor for style, and then 2), for rediscovery, and then also 3), for excellence. But there is more. He also stands for the dawning of a new age and the arrival of modernity.
The focus is on Naples, once the second largest city of Europe (and the world), a city still known for its vibrant music scene, as evidenced in a recent motion picture by the actor and director J. Turturro. Thousands and thousands (if not hundreds of thousands) of music manuscripts rest in Naples’s libraries. It is a huge legacy that is only in recent decades beginning to be rediscovered in earnest. The neglect is owed in great part to the fact that, since G. B. Pergolesi’s time, Naples has known long episodes of decline.
There is much to be said for the notion that modern music came into its own in the early eighteenth century in Naples, finally completely moving away from the polyphony of the Renaissance, and G. B. Pergolesi was part of this new development. Polyphony has its masterworks. But to the modern ear, it has a certain otherworldly quality.
The new Neapolitan style was known as the “sweet new style (dolce stil nuovo)”. G. B. Pergolesi surpassed all other composers in the practice of it. In contrast to some other composers, he for the most part avoids ostentation through the coloratura that is so well known from the vocal music of the baroque period. Indeed, a principal virtue of G. B. Pergolesi’s music is its simplicity—to the extent that many have been surprised how music that looks so simple on the page can sound so good when performed.
The Neapolitan style was the beginning of a new era that stretches all the way to the present day. Music reached a new and final plateau and that is where it stayed. True, music later became more sophisticated in all kinds of ways pertaining to composition, performance, and instrumentation. But I do not believe that much of it clearly surpasses the Neapolitan style in beauty. What is more, music lost all its humor in the nineteenth century. Furthermore, protagonists do not at great length and spectacularly die in eighteenth century operas. That is a relief.
The Neapolitan style still remains relatively less known in spite of the revival of recent decades. Accordingly, one comes upon statements here and there in various media by those who, when encountering it accidentally, are a little perplexed as to how they missed it.
One limitation of the style in question is that its achievements are mostly in vocal music. Its contributions to instrumental music are limited. L(eonardo) Leo’s (1694-1744) six concertos for cello are an exception rather than the rule.
This means that knowing Latin (for the sacred music) and Italian (for the secular music), sometimes the Neapolitan dialect of Italian for comedic operas (opera buffa), much increases the appreciation of the music in question, and especially of G. B. Pergolesi’s music.
The language factor may form a bit of a barrier and prevent the music in question from breaking out from a certain niche.
And evidently, to appreciate G. B. Pergolesi’s sacred music, it is necessary to realize that it is very, very Catholic.
In mathematics, it is always enlightening to know who influenced whom. By analogy, in the quest for an appreciation of G. B. Pergolesi’s style, it helps to listen to those that were close to him in place, time, and person, those three main coordinates of the human condition. Just two striking anecdotes.
Ch. Burney transmits the following first anecdote. As a rebellious 14-year old who had just mastered the traditional fine points of composing, G. B. Pergolesi wanted his friends to take him home so “that he might indulge his own fancies, and write such Music as was most agreeable to his natural perceptions and feelings” and Ch. Burney adds that, “[t]he instant he quitted the conservatorio, he totally changed his style, and adopted the style of [L(eonardo)] Vinci [(1690-1730)]… and of [J. A.] Hasse [(1699-1783)]”.
L. Vinci, the first great master of the dolce stil nuovo, is to be distinguished from L. da Vinci (1452-1519), he of the Mona Lisa, who may have been distantly related I read somewhere. The anecdote explains something about G. B. Pergolesi’s unique originality.
The design of the present acknowledgments is to recognize debts owed to others. In that regard, a small measure of inspiration has been derived from G. B. Pergolesi’s afore-mentioned insistence on escaping from certain conventions. I believe that the present paper has a valid point of view, even if this point of view may fall into the cracks located between the traditional partitions of academic writing [83] .
L. Vinci died in 1730, perhaps poisoned, just when G. B. Pergolesi began composing, and could not have been influenced by him. I refrain from detailing reports that J. A. Hasse, who composed prolifically both before and after G. B. Pergolesi’s short creative life (1730-1736), changed his style after becoming acquainted with G. B. Pergolesi’s music.
A special case is L(eonardo) Leo (1694-1744). He comes closest in style in many ways to G. B. Pergolesi. He ain’t G. B. Pergolesi. But still, his music constantly pleases and it exhibits many, many moments of exceptional beauty and simplicity combined. Music reached a pinnacle in early eighteenth century (early settecento) Naples. Has this pinnacle ever truly been surpassed?
A second anecdote is as follows. G. B. Pergolesi admired his older contemporary L. Leo as a mentor. L. Leo may have been the first to truly master counterpoint, I read somewhere, but I leave that to musicologists. I see one more possible indication of a new age dawning. According to one account, G. B. Pergolesi invited L. Leo to a performance of his Mass in F, upon completion of which L. Leo warmly and openly embraced him and highly praised him [84] [85] . Once familiar with G. B. Pergolesi’s style, L. Leo began imitating it, like other older Neapolitan composers, sometimes copying him almost note by note [86] . L. Leo was once famous all over Europe. How many have heard of him nowadays? Still, there has been a little bit of a revival.
G. B. Pergolesi died at age 26. The way in which he was on occasion spitting blood from about age 20 and the fact that his three siblings had all died by age 2 led those who knew him to strongly suspect that he was not going to last all that long. Also, one of his legs was atrophied. It all makes one wonder how such an eternal genius could inhabit such a crippled body. The way in which, in just six years of activity, he compiled a musical legacy that is unsurpassed if not unparalleled has been the subject of much wonder.
What if I had not accidentally heard G. B. Pergolesi’s Stabat mater a few years back on an inflight sound system and not caught, on radio, just a couple of years ago the tail end of a performance of his La Serva Padrona in English and then his entire Mass in F?
Or had not accidentally stumbled on G. Boole’s Laws of Thought in a bookstore in the late nineteen nineties? Or had not been pointed to J. C. Maxwell’s theory of electromagnetism by an engineering student taking my class in ancient Egyptian literature after looking in vain for inspiration concerning rational human intelligence in the architecture of the computer, computer programming, the electrochemistry of the neuron, neural network theory, and electricity in general.
The serendipity of it all seems rather curious to me. Whatever the circumstances of the serendipity, my personal experience of it has been the experience of a major paradigm shift in my own priorities. Am I allowed to interpret the shift metaphorically as a good omen for a major paradigm shift in the study of the prime sequence and in the study of rational human intelligence?