Analytical and Numerical Study of the Reflection/Transmission Coefficients in Slight Viscoelastic Medium ()
1. Introduction
The estimation of the reflection/transmission coefficients of the seismic waves is paramount for the investigation of the natural medium and to know their geometrical proprieties. In a perfect elastic medium, these coefficients are computed from the impedance contrast between two neighbouring layers [1] -[3] . In the viscoelastic media in addition to the impedance contrast, the viscoelasticity contrast between the two neighbouring layers should be taken into account. Usually the viscoelasticity of the medium is quantified by using the quality factor , which is inversely proportional to the energy loss
, which is inversely proportional to the energy loss  of the seismic wave:
of the seismic wave:
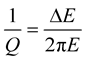 (1)
(1)
Buchen [4] has studied the propagation of the seismic wave SH in a layered and slight viscoelastic media. He used complex wave number to compute the reflection/transmission coefficients; the imaginary part of the wave number takes account the viscoelastic functionality. He noted that the difference between the reflection/transmission coefficients in the elastic and viscoelastic media is important when the quality factor contrast between two neighbouring layers is significant. Krebes [5] , has done the same study as Buchen [4] , but he considered the medium was highly viscoelastic. He noted that even by considering the medium highly viscoelastic, the equality of the quality factor between two neighbouring layers implies the independence of the reflection/transmission coefficients from the viscosity of the medium. The results of Buchen and Krebes, were confirmed by Carcione [6] , who studied also the effect of the anisotropy on the reflection/transmission coefficients.
In this paper, first we do an analytical study of the reflection/transmission coefficients in the slight viscoelastic medium. From this study we provide the analytical expressions of these coefficients for all possible incident wave (SH, P and SV), which allows to see clearly the contribution of the viscoelasticity on the reflection/ transmission coefficients. This analytical study is followed by a numerical example; through it we apply the analytical expressions on synthetic data. So far no study about the reflection/transmission coefficients in slight viscoelastic media has been more complete than this one.
2. Analytical Study
Reflection/transmission of plane seismic waves is a local phenomenon, involving local physical proprieties of two medium (1) and (2) at the discontinuity point . Locally, in the vicinity of the point
. Locally, in the vicinity of the point , we can consider that the interface is plane and having normal
, we can consider that the interface is plane and having normal  (Figure 1). At the point
(Figure 1). At the point  the seismic energy can be divided on reflected and transmitted, and it can generate two waves: reflected and transmitted.
the seismic energy can be divided on reflected and transmitted, and it can generate two waves: reflected and transmitted.
An incident P wave as an incident SV wave can generate reflected P or SV wave and transmitted P or SV wave. However, an incident SH wave can generates only reflected or transmitted SH wave. The reflected or transmitted waves which are different from the incident wave, they are called converted waves, such P-SV reflection for example.
In this study the incident wave is indicated by the subscript , the reflected wave by the subscript
, the reflected wave by the subscript 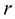 and the transmitted wave by the subscript
and the transmitted wave by the subscript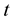 . The viscoelastic reflection/transmission coefficient are designed by the variables
. The viscoelastic reflection/transmission coefficient are designed by the variables .
.
In this section we put just the main equations leading to the  coefficients. More details are given in the thesis of Bouchaala [7] .
coefficients. More details are given in the thesis of Bouchaala [7] .
3. Displacement Continuity
The displacement of the wave particles at the instant  and the position
and the position 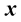 can be expressed as [8] ,
can be expressed as [8] ,
 (2)
(2)
where  is the source term,
is the source term, 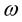 is the circular frequency,
is the circular frequency,  is the amplitude vector at the position
is the amplitude vector at the position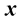 . In the orthonormal basis
. In the orthonormal basis  (Figure 2) the amplitude vector
(Figure 2) the amplitude vector  has the components
has the components  and can be written as,
and can be written as,
 (3)
(3)
 is the slowness, which can be computed from the velocity
is the slowness, which can be computed from the velocity , the propagation direction
, the propagation direction  and the quality factor
and the quality factor  by:
by:

Figure 1. Incident, reflected and transmitted waves in a medium composed from two layers (1) and (2), I is the intersection point between the incident wave and the interface, N is the unit vector normal to the interface at the point I.
 (4)
(4)
In the elastic case the slowness vector is real and independent form ,
,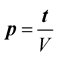 .
.
The continuity of the displacement vector at the point  (Figure 3) is expressed as:
(Figure 3) is expressed as:
 (5)
(5)
The displacement at the point  in the medium (1) is due to the incident and reflected waves:
in the medium (1) is due to the incident and reflected waves:
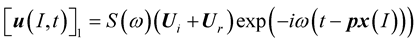 (6)
(6)
The displacement at the point  in the medium (2) is due only to the transmitted wave:
in the medium (2) is due only to the transmitted wave:
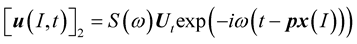 (7)
(7)
We use the expressions of the displacement given in the Equations (6) and (7) in the continuity Equation (5) and we obtain:
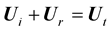 (8)
(8)
The projection of the Equation (8) on the unit vector  (Figure 3) gives:
(Figure 3) gives:
 (9)
(9)

Figure 3. The direct orthonormal basis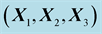 , the vector
, the vector 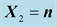 is perpendicular to the figure.
is perpendicular to the figure.
And in the incident plane 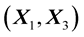 (Figure 3) it gives:
(Figure 3) it gives:
 (10)
(10)
4. Stress Continuity
The continuity condition of stress vector at the point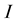 , is expressed by the following equation:
, is expressed by the following equation:
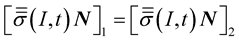 (11)
(11)
where  is the stress vector at the point
is the stress vector at the point , generated by the incident and the reflected waves (propagating in the medium (1)), and applied on the elementary surface having a normal vector
, generated by the incident and the reflected waves (propagating in the medium (1)), and applied on the elementary surface having a normal vector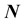 .
.
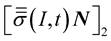 is the stress vector at the point
is the stress vector at the point 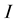 generated by the transmitted wave (propagating in the medium (2)), and applied on the elementary surface having a normal vector
generated by the transmitted wave (propagating in the medium (2)), and applied on the elementary surface having a normal vector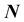 .
.
In the isotropic media, the generalized Hook’s law can be simplified as:
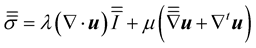 (12)
(12)
where  and
and 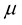 are the complex Lame coefficients, their imaginary parts contain the viscoelastic functionality of the medium. In the elastic case these coefficients are real.
are the complex Lame coefficients, their imaginary parts contain the viscoelastic functionality of the medium. In the elastic case these coefficients are real.
The projection of the Equation (12) in the orthonormal basis  (Figure 3), leads to the following expression of stress vector
(Figure 3), leads to the following expression of stress vector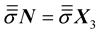 :
:
 (13)
(13)
where
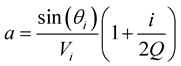 ,
, 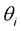 is the incident angle (14)
is the incident angle (14)
So, by using the Equation (14), the continuity condition (12) in theorthonormal basis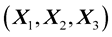 , we get a system of three equations:
, we get a system of three equations:
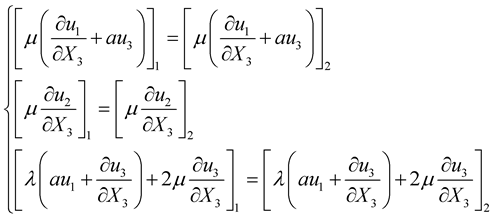 (15)
(15)
From the Equation (2) the derivation of the components of the vector displacement can be given as,
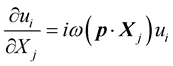 (16)
(16)
The system of Equation (15) contains one equation involving only the second component , corresponding to the displacement of the wave SH and also two other equations, involving the first and the third components,
, corresponding to the displacement of the wave SH and also two other equations, involving the first and the third components,  and
and , corresponding to the displacement of P and SV waves, respectively. This means, that the reflection/transmission problem can be divided in two sub-problems: P-SV and SH.
, corresponding to the displacement of P and SV waves, respectively. This means, that the reflection/transmission problem can be divided in two sub-problems: P-SV and SH.
 (17)
(17)
 (18)
(18)
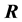 and
and  indicate the matrix of the reflection and transmission coefficients, respectively.
indicate the matrix of the reflection and transmission coefficients, respectively.
We use the derivation in the Equation (16) to get the projection in the orthonormal basis  of displacement and stress vectors due to the incident, reflected and transmitted waves of SH, SV and P waves, which are given in the Tables 1-4.
of displacement and stress vectors due to the incident, reflected and transmitted waves of SH, SV and P waves, which are given in the Tables 1-4.

Table 1. Component in the basis  of displacement vectors at the point
of displacement vectors at the point 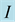 for incident, reflected and transmitted waves (SH Reflection/Transmission).
for incident, reflected and transmitted waves (SH Reflection/Transmission).

Table 3. Component in the basis 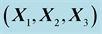 of the displacement vector at point
of the displacement vector at point  for incident, reflected and transmitted waves (Reflection/Transmission P-SV).
for incident, reflected and transmitted waves (Reflection/Transmission P-SV).

Table 4. Component in the basis 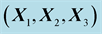 of stress vector at
of stress vector at  due to incident, reflected, and transmitted waves (Reflection/Transmission P-SV).
due to incident, reflected, and transmitted waves (Reflection/Transmission P-SV).
Before starting our analytical development, we remind the following results:
 (19)
(19)
where 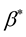 and
and  are the complex
are the complex 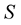 and
and 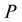 wave velocities which can be expressed from the real velocities
wave velocities which can be expressed from the real velocities 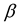 and
and 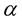 and the quality factors
and the quality factors 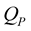 and
and 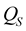 (see Appendix).
(see Appendix).
5. SH Problem
We assume SH incident wave, with the amplitude vector,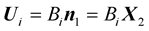 . The continuity Equations (9) and (15) at the interface show that the incident SH wave, generates only SH waves, reflected or transmitted.
. The continuity Equations (9) and (15) at the interface show that the incident SH wave, generates only SH waves, reflected or transmitted.
After using the projection of the stress vector in the basis 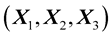 given in the Table 2 and replacing
given in the Table 2 and replacing 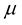 by its expression in Equation (19), the Equation (15) becomes,
by its expression in Equation (19), the Equation (15) becomes,
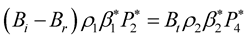 (20)
(20)
After using the Equation (9), the Equation (20) can be written as,
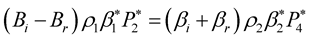 (21)
(21)
or
 (22)
(22)
The 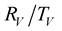 coefficients are defined as,
coefficients are defined as,
 (23)
(23)
After dividing the Equations (21) and (22) by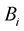 , we obtain expression of
, we obtain expression of 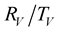 coefficients
coefficients
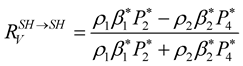 (24)
(24)
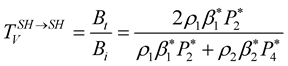 (25)
(25)
We replace the parameters indicated by an asterisk in Equations (24) and (25) by their expressions shown in the Appendix, to obtain the final expressions of the 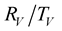 coefficients,
coefficients,
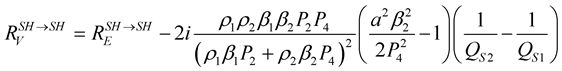 (26)
(26)
 (27)
(27)
where 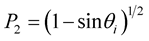 and
and .
.
The terms  and
and 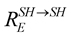 in the Equations (26) and (27), corresponds respectively to the reflection and transmission coefficients of the elastic media which are dependent on the impedance contrast
in the Equations (26) and (27), corresponds respectively to the reflection and transmission coefficients of the elastic media which are dependent on the impedance contrast  between the two media. The second term of the equations is due to the viscosity effect on the
between the two media. The second term of the equations is due to the viscosity effect on the 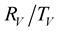 coefficients, it is proportional to the quality factor contrast,
coefficients, it is proportional to the quality factor contrast, 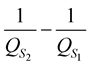 between the two media. This means that with a zero contrast in the quality factor, the
between the two media. This means that with a zero contrast in the quality factor, the 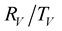 coefficients are similar to those of the elastic case.
coefficients are similar to those of the elastic case.
6. P-SV Problem
P and SV incident waves can generate reflected or transmitted P and SV waves. After using the projection of the displacement and stress vector in the basis 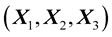 given in the Table 3 and Table 4, we replace
given in the Table 3 and Table 4, we replace 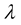 and
and  by their expressions in Equation (19), thecontinuity Equations (9) and (15) can be written respectively asFor P incident wave
by their expressions in Equation (19), thecontinuity Equations (9) and (15) can be written respectively asFor P incident wave
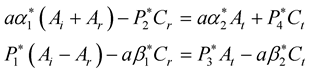 (27)
(27)
 (28)
(28)
For SV incident wave,
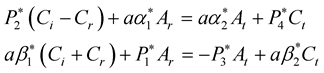 (29)
(29)
 (30)
(30)
The 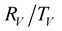 coefficients are defined asFor P incident wave,
coefficients are defined asFor P incident wave,
 (31)
(31)
For S incident wave,
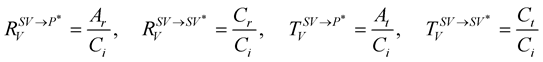 (32)
(32)
By combining the Equations (27) to (32),  coefficients can be expressed in matrix formFor P incident wave,
coefficients can be expressed in matrix formFor P incident wave,
 (33)
(33)
For SV incident wave,
 (34)
(34)
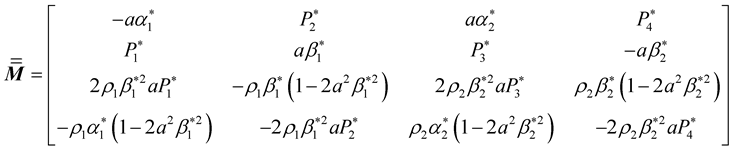 (35)
(35)
We invert the matrix 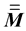 in the Equations (33) and (34), then we obtain the analytical expressions of all possible reflection and transmission coefficients from P and SV incident waves, under the assumption that
in the Equations (33) and (34), then we obtain the analytical expressions of all possible reflection and transmission coefficients from P and SV incident waves, under the assumption that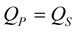 :
:
 (36)
(36)
Such the SH incident wave case, the above equations can be divided in two terms, the first one corresponds respectively to the reflection and transmission coefficients of the elastic media and the second one corresponds to the contribution of the viscosity. The contribution is proportional to the contrast of the viscosity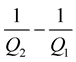 therefore if the quality factor contrast equals zero, we get back at the elastic case.
therefore if the quality factor contrast equals zero, we get back at the elastic case.
The exact expressions of the second terms in Equation (36) are given in the Appendix.
7. Numerical Study
Synthetic Data
To have further insight about the effect of the viscoelasticity on the  coefficients, we apply the above expressions of the coefficients on a synthetic data. We assume two cases, in the first case we assume a low impedance contrast between the medium (1) and the medium (2), and in the second case we assume a big impedance contrast between the two media (Table 5). The medium (1) in the first case has similar characteristic as a sandstone formation and as marlstone formation in the second case. The medium (2) has similar characteristic as a limestone formation in the two cases [9] .
coefficients, we apply the above expressions of the coefficients on a synthetic data. We assume two cases, in the first case we assume a low impedance contrast between the medium (1) and the medium (2), and in the second case we assume a big impedance contrast between the two media (Table 5). The medium (1) in the first case has similar characteristic as a sandstone formation and as marlstone formation in the second case. The medium (2) has similar characteristic as a limestone formation in the two cases [9] .
We should respect the slight viscosity assumption, for the choice of the quality factor values . For each case and each reflection or transmission, we choose:
. For each case and each reflection or transmission, we choose: 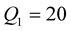 and
and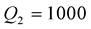 , in the first time then the inverse:
, in the first time then the inverse:  and
and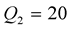 . The curves of the
. The curves of the 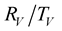 coefficients versus incidence angles for the chosen values of the quality factor, are compared to the elastic case
coefficients versus incidence angles for the chosen values of the quality factor, are compared to the elastic case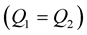 .
.
8. Results
The curves (Figures 4-13) of the 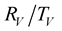 coefficients from all possible incident waves (P-SV, SH), show that the viscoelasticity of the medium disturbs there flection/transmission-coefficients around the critical angles (Table 6 and Table 7). The difference between the elastic
coefficients from all possible incident waves (P-SV, SH), show that the viscoelasticity of the medium disturbs there flection/transmission-coefficients around the critical angles (Table 6 and Table 7). The difference between the elastic 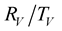 coefficients, indicated by the black color
coefficients, indicated by the black color

Table 6. Critical angles (Incident wave P).

Table 7. Critical angles (Incident wave S).
in the figures and the viscoelastic coefficients indicated by the blue and red colors can be significant. As we can note in the first case, where the modulus viscoelastic reflection coefficient around the critical angle reach 1.4, bigger than 1 because of the changing in the phase also, while in the elastic case the modulus is equal to 0.9.
The Figures 4-13 show also that when the number of the critical angles is high, as in the case 2, the  coefficients are more affected by the viscoelasticity of the medium.
coefficients are more affected by the viscoelasticity of the medium.
9. Conclusions
The above results show that in the viscoelastic media,  coefficients between two neighboring layers depend on the contrast of their quality factor. The effect of the contrast is effective around the critical angles, which depends on the incidence angle and the velocities of each layer. The number of the critical angles increases when the velocity contrast is large and in this case the
coefficients between two neighboring layers depend on the contrast of their quality factor. The effect of the contrast is effective around the critical angles, which depends on the incidence angle and the velocities of each layer. The number of the critical angles increases when the velocity contrast is large and in this case the  coefficients are more disturbed by the viscoelasticity of the medium. We noted that when the upper layer has bigger attenuation than the lower layer
coefficients are more disturbed by the viscoelasticity of the medium. We noted that when the upper layer has bigger attenuation than the lower layer , the curves display a discontinuity at the critical angle.
, the curves display a discontinuity at the critical angle.
The interpretation of the above observations is difficult to interpret and we do not know if it has a physical meaning or just a mathematical artefact. More understanding of the reflection/transmission mechanism in the viscoelastic media is necessary to interpret these results.
Appendix

Expression of the reflection-transmission coefficients (P-SV) in isotropic, inhomogeneous and viscoelastic medium
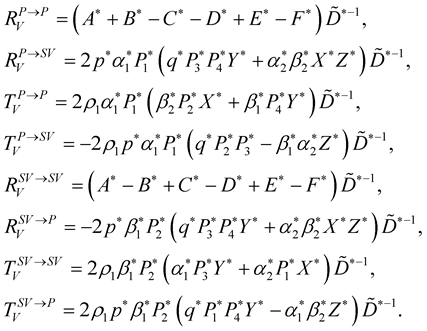
with: 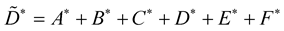

and 

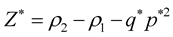

After doing the below substitution in the above expressions of reflection-transmission coefficients,

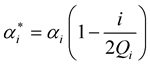 for
for 
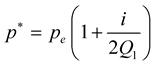
and  for P incident wave and
for P incident wave and 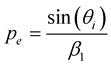 for S incident wave we obtain:
for S incident wave we obtain:

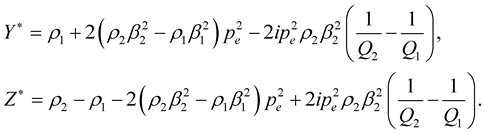
And also,

Now we compute 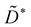 and
and 

With 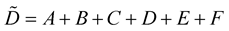


Table A1. Component in the basis  of stress vector at
of stress vector at  due to incident, reflected, and transmitted waves (Reflection/Transmission P-SV).
due to incident, reflected, and transmitted waves (Reflection/Transmission P-SV).