The Cauchy Problem for the Heat Equation with a Random Right Part from the Space Subφ (Ω) ()
1. Introduction
The subject of this work is at the intersection of two branches of mathematics: mathematical physics and stochastic processes.
The physical formulation of problems of mathematical physics with random factors was studied by Kampe de Feriet [1] . In the works [2] and [3] , a new approach studying the solutions of partial differential equations with random initial conditions was proposed. The authors investigate the convergence in probability of the sequence of function spaces of partial sums approximating the solution of a problem. The mentioned approach was used in the works [4] -[7] . In the paper [3] , the application of the Fourier method for the homogeneous hyperbolic equation with Gaussian initial conditions is justified. The conditions of the existence of the classical solution of this equation in terms of correlation functions are also studied. Homogeneous hyperbolic equation with random initial conditions from the space  is considered in [8] -[11] . The model of a solution of a hyperbolic type equation with random initial conditions was investigated in the papers [12] [13] . There is a study on a boundary-value problem of mathematical physics for the inhomogeneous hyperbolic equation with
is considered in [8] -[11] . The model of a solution of a hyperbolic type equation with random initial conditions was investigated in the papers [12] [13] . There is a study on a boundary-value problem of mathematical physics for the inhomogeneous hyperbolic equation with  -subgaussian in right part [8] [14] . The parabolic type equations of Mathematical Physics with random factors of Orlicz spaces have been studied in the papers [15] [16] . Further references can be found in [8] [17] -[21] .
-subgaussian in right part [8] [14] . The parabolic type equations of Mathematical Physics with random factors of Orlicz spaces have been studied in the papers [15] [16] . Further references can be found in [8] [17] -[21] .
We consider a Cauchy problem for the heat equations with a random right part. We study the inhomogeneous heat equation on a line with a random right part. We consider the right part as a random function of the space . The Gaussian stochastic process with zero mean belongs to
. The Gaussian stochastic process with zero mean belongs to  [22] . The conditions of existence with probability one of the classical solution of this problem are investigated. For such a problem has been got the estimation for the distribution of the supremum solution.
[22] . The conditions of existence with probability one of the classical solution of this problem are investigated. For such a problem has been got the estimation for the distribution of the supremum solution.
The paper consists of the introduction and three parts. Section 2 contains necessary definitions and results of the theory of the  space. In Section 3, we consider heat equations with random right-hand side. For such problem conditions of existence, with probability one, of classical solution with random right-hand side from the space
space. In Section 3, we consider heat equations with random right-hand side. For such problem conditions of existence, with probability one, of classical solution with random right-hand side from the space  are found. The estimation for distribution of supremum of this problem has been got in Section 4.
are found. The estimation for distribution of supremum of this problem has been got in Section 4.
2. Random Processes from  Space
Space
Definition 1. [23] An even continuous convex function ,
,  such that
such that  and
and 
for  and
and  is called an
is called an  function.
function.
Definition 2. [21] We say an  function
function  satisfies the
satisfies the  condition if there exist constants
condition if there exist constants ,
,  ,
,  such that
such that 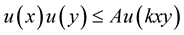 for all
for all ,
, .
.
Lemma 1. [21] Let  be an
be an  function. Then 1.
function. Then 1.  for
for  and
and ;
;
2.  for
for  and
and ;
;
3.  for
for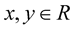 ;
;
4. The function  is non decreasing for
is non decreasing for .
.
Lemma 2. [21] Let  be the inverse to an
be the inverse to an  function
function  for
for . Then
. Then  is a convex increasing function such that 1.
is a convex increasing function such that 1.  for
for  and
and ;
;
2.  for
for  and
and ;
;
3.  for
for ;
;
4. the function  is nonincreasing for
is nonincreasing for .
.
Definition 3. [23] Let  be an
be an  function. The function
function. The function  is called the YoungFenchel transform of the function
is called the YoungFenchel transform of the function . The function
. The function  is an
is an  function as well.
function as well.
Let  be a standard probability space.
be a standard probability space.
Definition 4. [21] Let  be an
be an  function for which there exist constants
function for which there exist constants  and
and  such that
such that 
 for
for . The set of random variables
. The set of random variables ,
,  , is called the space
, is called the space  generated by the
generated by the  function
function  if
if  and there exists a constant
and there exists a constant  such that
such that  for all
for all .
.
The space  is a Banach space with respect to the norm [21]
is a Banach space with respect to the norm [21]  .
.
Definition 5. [23] The stochastic process  belongs to space
belongs to space ,
,  if
if  for all
for all .
.
Remark 1. [24] The Gaussian stochastic process  with zero mean belongs to
with zero mean belongs to , where
, where  and
and .
.
A Family of Strongly  Random Variables and a Family Strongly
Random Variables and a Family Strongly  Stochastic Processes
Stochastic Processes
Lemma 3. [21] If , then there exists a constant
, then there exists a constant  such that
such that .
.
Definition 6. [21] The random variable  is called strongly
is called strongly ,
,  random variable if
random variable if .
.
Properties and applications of  random variables and stochastic processes from
random variables and stochastic processes from  can be found in [21] .
can be found in [21] .
Definition 7. [7] A family  of random variables
of random variables 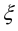 of the space
of the space  is called
is called  family if
family if
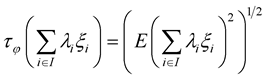
for all , where
, where  is at most countable and
is at most countable and ,
, .
.
Theorem 1. [7] Let  be a strongly
be a strongly  family of random variables. Then the linear closure
family of random variables. Then the linear closure  of the family
of the family  in the space
in the space  and in the mean square sense is a strongly
and in the mean square sense is a strongly  family.
family.
Definition 8. [21] The stochastic process  is called an
is called an  process if the family of random variables
process if the family of random variables  is an
is an .
.
Theorem 2. [7] Let  be a family of jointly strongly
be a family of jointly strongly  stochastic processes. Then
stochastic processes. Then  is a measurable space. If
is a measurable space. If  is a family of measurable functions in
is a family of measurable functions in  and the integral
and the integral  is well defined in the mean square sense, than the family of random variables
is well defined in the mean square sense, than the family of random variables  is an
is an  family.
family.
Theorem 3. [9] Let  be the
be the  -dimensional space,
-dimensional space,
 ,
,  ,
,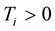 .
. . Assume that the process
. Assume that the process  is separable and
is separable and
 where
where  is a monotone increasing continuous function such that
is a monotone increasing continuous function such that  as
as . We also assume that
. We also assume that ,where
,where  and
and  is the inverse function to
is the inverse function to . If the processes
. If the processes  converge in probability to the process
converge in probability to the process  for all
for all , then
, then  converge in probability in the space
converge in probability in the space .
.
Theorem 4. [9] Let  and let
and let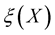 ,
,  , be a separable random field such that
, be a separable random field such that . Put
. Put  and assume that the partial derivatives
and assume that the partial derivatives
 and
and
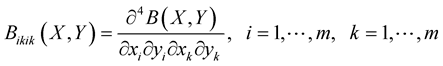
exist. Let there exist a monotone increasing continuous function ,
,  , such that
, such that  as
as  for
for ,
,  ,
,  and
and ,
, . Assume that
. Assume that
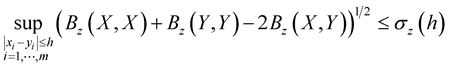
If  for all
for all  and for sufficiently small
and for sufficiently small  where
where , then with probability one the partial derivatives
, then with probability one the partial derivatives ,
,  ,
,  , exist and are continuous.
, exist and are continuous.
3. The Heat Equations with Random Right Part
We consider the Cauchy problem for the heat equation
 (1)
(1)
 , subject to the initial condition
, subject to the initial condition
 (2)
(2)
Let the function  is a random field sample continuity with probability one from the space
is a random field sample continuity with probability one from the space , such that
, such that ,
, . Let us denote
. Let us denote . Let
. Let  be a continuous function. Problem when the function
be a continuous function. Problem when the function  nonrandom has been seen in [25] .
nonrandom has been seen in [25] .
Lemma 4. Let  is a random field, sample continuity for each
is a random field, sample continuity for each  with probability one, there is a continuous derivative
with probability one, there is a continuous derivative  for
for  and satisfy condition
and satisfy condition
 (3)
(3)
Then for the function  for each
for each  the integral Fourier transform
the integral Fourier transform
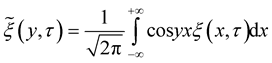
exist and .
.
Proof. Since, by Fubini’s theorem,  , we deduce that the integral
, we deduce that the integral  exist with probability one, and therefore the integral
exist with probability one, and therefore the integral , and therefore it implies from [26] that the integral Fourier transform
, and therefore it implies from [26] that the integral Fourier transform

exist, and the inverse integral Fourier transform
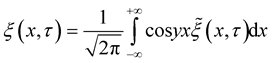
exist.
Theorem 5. Let the conditions of Lemma 4 be satisfied and
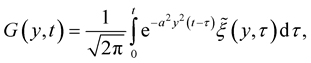
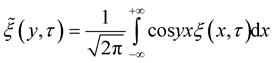
and
 (4)
(4)
If the following integrals exist
 ,
,  ,
,
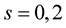
and for all 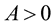 and
and  there exists a sequence
there exists a sequence ,
,  for
for , such that the sequence of integrals
, such that the sequence of integrals
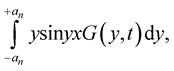 (5)
(5)
 (6)
(6)
converges in probability, uniformly for ,
,  , then
, then  is the classical solution to the problem (1) and (2).
is the classical solution to the problem (1) and (2).
Proof. Since the integrals (5) and (6) converges in probability uniformly for ,
,  , there exists a subsequence
, there exists a subsequence ,
,  as
as , such that
, such that

converges with probability one to
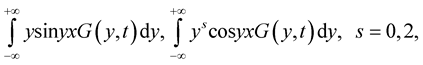
uniformly for ,
,  , Let
, Let
 (7)
(7)
By deriving (7) with respect to  and
and , we easily see that
, we easily see that
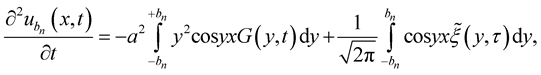
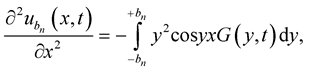

 Since for
Since for 
 converges to
converges to , and
, and  converges to
converges to  uniformly for
uniformly for ,
,  with probability one, we conclude that
with probability one, we conclude that  satisfies Equation (1).
satisfies Equation (1).
Indeed, 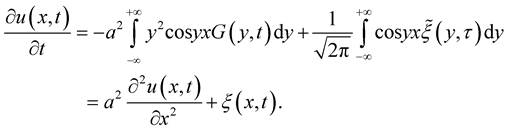
Lemma 5. [9] Let  be a random field, sample continuity from the space
be a random field, sample continuity from the space . Let
. Let  be the correlation function of the field
be the correlation function of the field . For all
. For all  assume that:
assume that:
1. The derivatives  exist;
exist;
2 
3. , at
, at  or
or .
.
Then Lebesgue integrals
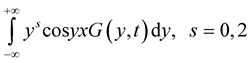
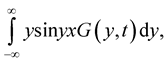
exist with probability one.
Proof. We shall prove the existence of the integral
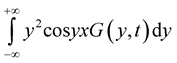
For existence of this integral with probability one it is enough to prove that there exists following integral

There is an inequality
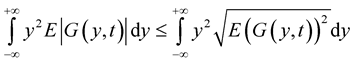
Consider

Integrating by parts and using the conditions of the lemma, we obtain for y ≠ 0
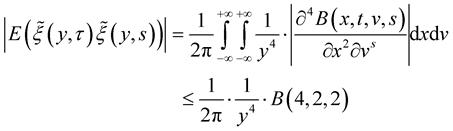
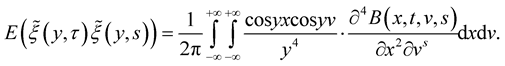
Then

Therefore
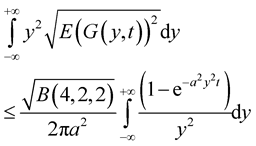
for . The latter integral converges under
. The latter integral converges under . The existence of integrals
. The existence of integrals ,
,  can be proved similarly.
can be proved similarly.
Lemma 6. [15] Let a function ,
,  and
and  be such that:
be such that:
1. 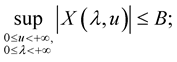
2.  for all
for all ,
, . Let
. Let ,
,  be a continuous increasing function such that
be a continuous increasing function such that  for all
for all , and the function
, and the function 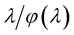 is increasing for
is increasing for , and for some constant
, and for some constant .
.
Then 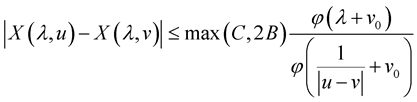
for all  and
and .
.
Corollary 1. Let in the conditions of Lemma 6 the function ,
,  ,
, . Then
. Then
 (8)
(8)
for all .
.
Proof. Indeed, it is easy to show that the function
 increases with
increases with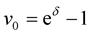 . Therefore in Lemma 6 taking function
. Therefore in Lemma 6 taking function 

 we obtain the inequality 8.
we obtain the inequality 8.
Corollary 2.
 . (9)
. (9)
 . (10)
. (10)
for some .
.
Remark 2. If in the conditions of Corollary 2 ,
,  , then for sufficiently small
, then for sufficiently small  inequality (9) and (10) will have the form
inequality (9) and (10) will have the form
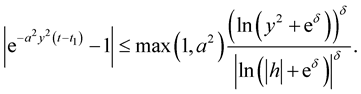

Let 


Theorem 6. Let  be a random field, sample continuous with probability one from the
be a random field, sample continuous with probability one from the  and the conditions of Lemma 4 and Lemma 5 hold,
and the conditions of Lemma 4 and Lemma 5 hold,
 For
For , where
, where  is a monotone increasing continuous function such that
is a monotone increasing continuous function such that  as
as , moreover,
, moreover,
 , (11)
, (11)
where , and
, and  is the inverse function to
is the inverse function to . Then the function
. Then the function  which is represented in the form (4) is a classical solution to the problems (1) and (2).
which is represented in the form (4) is a classical solution to the problems (1) and (2).
Proof. This theorem follows from Theorems 5 and 3.
Example 1. Let  be a function such that
be a function such that , for some
, for some  and all
and all . Then
. Then 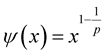 for
for  and condition (11) holds for all
and condition (11) holds for all 
 (12)
(12)
Condition (12) holds if , for
, for ,
,
 ,
, . In this case, the condition of Theorem 6 is satisfied if for
. In this case, the condition of Theorem 6 is satisfied if for  there exist constants
there exist constants  such that
such that
 , (13)
, (13)
For  all
all , and sufficiently small
, and sufficiently small .
.
Theorem 7. Let 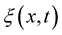 be a random field, sample continuous with probability one from the space
be a random field, sample continuous with probability one from the space , where
, where  is a function such that
is a function such that  for some
for some  and all
and all  and the conditions of Lemma 4 and Lemma 5 hold and
and the conditions of Lemma 4 and Lemma 5 hold and 
 ,
,  for some
for some ,
,  ,
, . Then the function
. Then the function  which is represented in the form (4) is classical solution to the problems (1) and (2).
which is represented in the form (4) is classical solution to the problems (1) and (2).
Proof. It follows from Lemma 5 that there exist integrals with probability one
 ,
, .
.
According to Theorem 5 to make the function  be the solution of problems (1) and (2) it is sufficient to prove that integrals (5) and (6) converge uniformly in probability in
be the solution of problems (1) and (2) it is sufficient to prove that integrals (5) and (6) converge uniformly in probability in ,
,  to the integrals
to the integrals
 ,
,  for any
for any ,
, . According to Theorem 6, using the Example (1), to make integral (5) and (6) converge in probability in
. According to Theorem 6, using the Example (1), to make integral (5) and (6) converge in probability in  the following conditions must hold
the following conditions must hold

Using generalized Minkovskoho inequality we obtain
 (14)
(14)
Let  and for sufficiently small
and for sufficiently small , using the inequality (10), we have
, using the inequality (10), we have
 (15)
(15)
Consider

It follows from Lemma 4 that 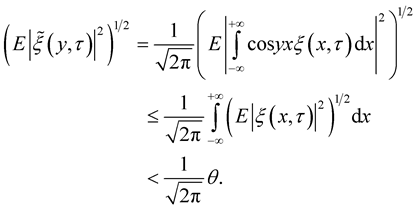
Therefore
 (16)
(16)
Let  then
then
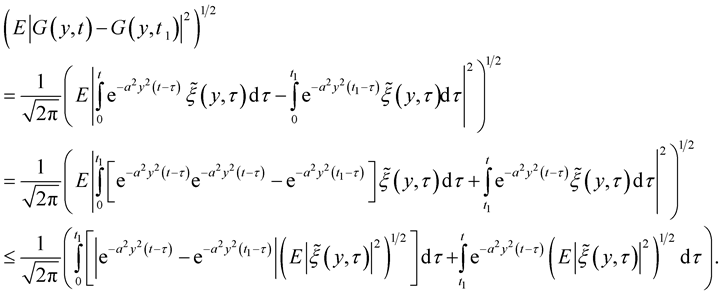
Let  and for sufficiently small
and for sufficiently small , using the inequality (9), we have
, using the inequality (9), we have
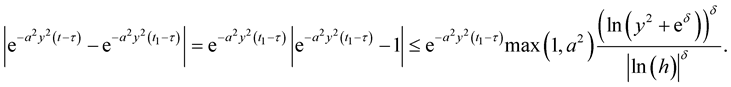
Therefore
 (17)
(17)
Thus we obtain from (14), (15), (16) and (17) that
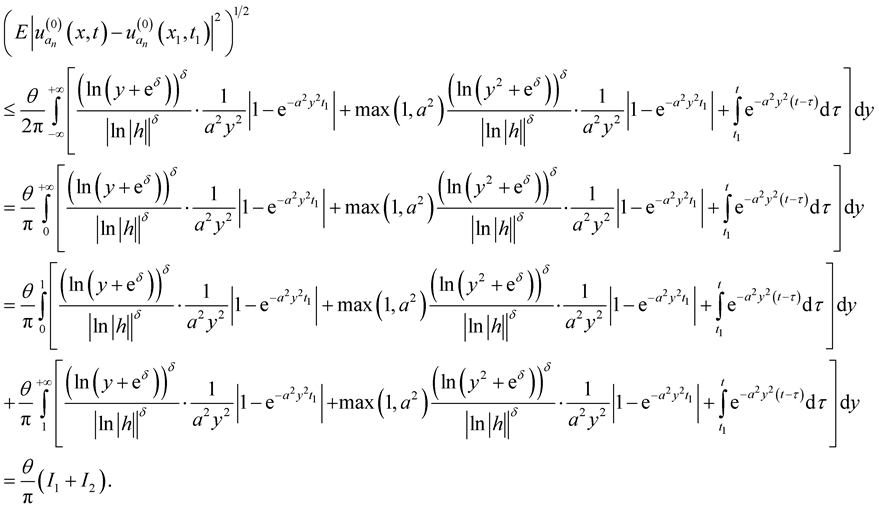
Consider
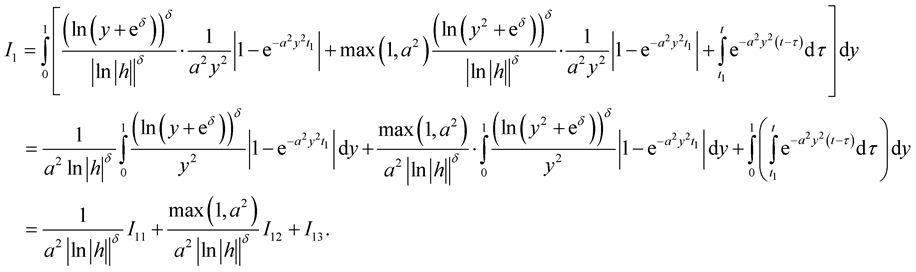
Since , we have
, we have
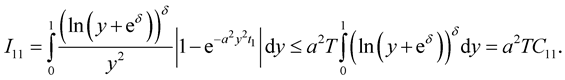
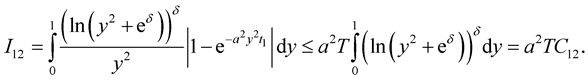
Using that ,
,  , then the
, then the  and for sufficiently small
and for sufficiently small , we have
, we have
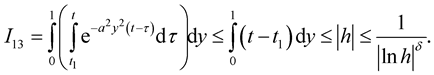
So we have

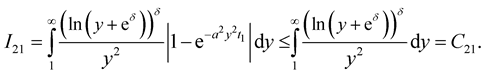
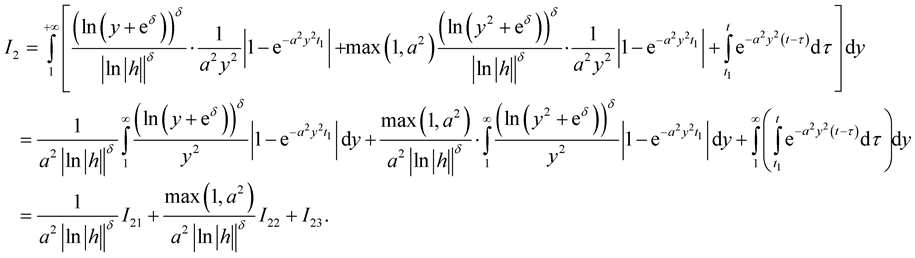
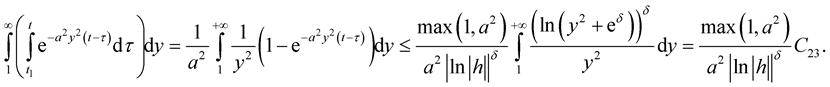
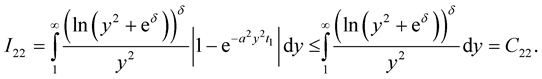
Therefore  Then for
Then for , we have
, we have where
where
 ,
,  are some constants.
are some constants.
Consider
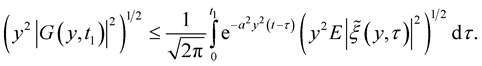

From Lemma 4, we obtain
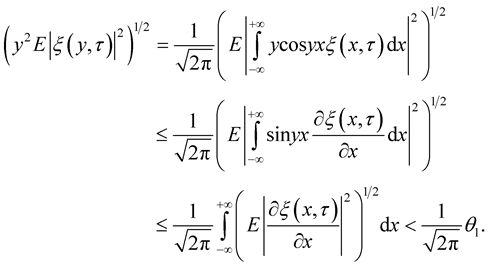
Similarly 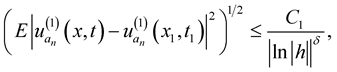
where ,
,  are some constants.
are some constants.
Consider
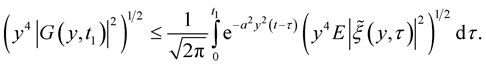
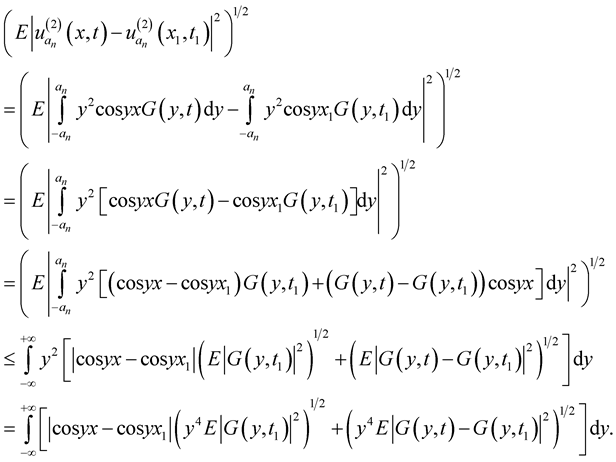
From Lemma 4 we obtain
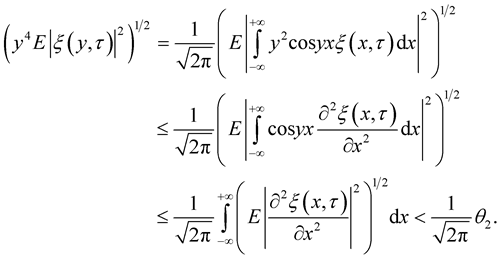
Then 
where 
 are some constants.
are some constants.
4. Estimates of the Distribution of the Supremum of a Solution
Theorem 8. [9] Let  be the
be the  -dimensional space,
-dimensional space,  ,
,  ,
, . Assume that
. Assume that  is separable and
is separable and . If
. If where
where  is a monotone increasing continuous function such that
is a monotone increasing continuous function such that  as
as , and
, and
 , where
, where  and
and  is the inverse function to
is the inverse function to . Then
. Then , for all
, for all  and
and , where
, where

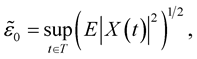

Theorem 9. Let the conditions of Theorem 6 hold
 .
.
where
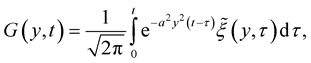
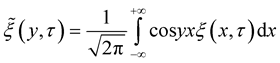
 . Then
. Then
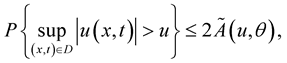
for all  and
and , where
, where
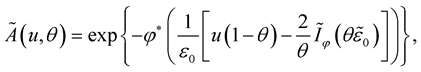
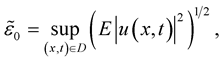

where  is a monotone increasing continuous function such that
is a monotone increasing continuous function such that  as
as , and
, and  is the inverse function to
is the inverse function to .
.
Proof. This theorem follows from Theorem 8.