The Ratcheting Behaviour of Stainless Steel Pressurized Piping Elbows Subjected to Dynamic Out-of-Plane Moments ()
1. Introduction
Pressurized piping is widely used in power plant, electric, and chemical industries. In addition to fluid pressure, piping components have to endure bending loads due to seismic loading. The plastic accumulation namely ratcheting occur in the structures under this kind of loading and lead to failures. Thus, during the design of pressurized piping today, especially that used in power plant industries, ratcheting and ratcheting fatigue must be under consideration. Experimental works to study the ratcheting of the straight pipes, elbows, branch and even piping system have also been carried out by EPRI (English [1] , Ranganath, Hwang and Tagart [2] , Yahiaoui et al. [3] -[8] , Hassan et al. [9] -[13] , Igaria et al. [14] , Feaugas and Gaudin [15] , Chen et al. [16] [17] ).
Yahiaoui et al. [8] tested 16 pairs of long and short radius 90 elbow pipes of carbon and stainless steel under conditions of steady internal pressure and either in-plane or out-of-plane resonant bending to simulate seismic conditions. It was shown that the maximum ratcheting strain occurred at crown and intrados positions for inplane bending. For out-of-plane bending, the direction of maximum strain was found to be at about 45˚ between the hoop and axial directions. Also, the direction of highest ratcheting was found to be along the hoop direction rather than the direction of maximum principal strain. Chen et al. [16] [17] experimentally studied multiaxial ratcheting for pressurized low carbon steel elbows under reversed bending. It was shown that the maximum ratcheting strain occurred mainly in the hoop direction at flanks.
Based on the Armstrong-Frederick nonlinear kinematic hardening rule, many constitutive models have been constructed to simulate the unaxial and multiaxial ratcheting of materials characterized by cyclic hardening or cyclic stable behaviors. A great number of cyclic plasticity constitutive models have been proposed in the last two decades for prediction of ratcheting such as Chaboche and his co-workers models [18] -[21] , Voyiadjis and his Co-workers [22] [23] , Ohno and Wang models [24] [25] , Ohno [26] , Hassan and Kyriakides [9] , Hassan et al. [10] , Hassan and Kyriakides [11] [12] , McDowell [27] [28] , Abdel Karim and Ohno [29] , Bari and Hassan [30] -[32] , Kang et al. [33] , Chen et al. [16] [17] [34] -[37] , Zakavi et al. [38] . Most of these models are based on the Armstrong-Frederick kinematic hardening rule with a modification of the dynamic recovery term.
2. Materials and Methods
In this paper, the nonlinear kinematic hardening model is used to study the ratcheting behavior of stainless steel piping elbows under conditions of steady internal pressure and dynamic out-of-plane bending at frequencies typical of seismic excitations. The experimental tests [8] are modeled and FE data obtained. The two sets of results are compared with each other.
3. Nonlinear Kinematic Hardening Models
The linear and nonlinear kinematic hardening models were first proposed by Prager [39] and Armstrong-Frederick [40] respectively. Nonlinearities are given as a recall term in the Prager rule. The kinematic hardening plasticity models are proposed to model the inelastic behavior of materials that are subjected to repeated loading. The nonlinearities are given as a recall term in the Prager rule [41] :
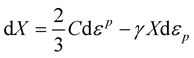(1)
where 
is the back stress tensor, 
is the equivalent plastic strain rate, 
and 
are two material dependent coefficients in the Armstrong–Frederick kinematic hardening model, and 
stands for the linear kinematic rule. The evolution equation of hardening can be integrated analytically to give [41] :
(2)
where 
according to the direction of flow, and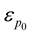 
and 
are the initial values, for example at the beginning of each plastic flow.
4. Review of Experimental Set-Up [8]
The experimental set-up for testing piping elbows under out-of-plane bending has been reported in reference [8] . Four pairs stainless steel of 90˚, 2 inch nominal pipe size (corresponding to an outside diameter of 60.3 mm), welding elbows were used. two thicknesses (extra strong, schedule 80 equivalent to a 5.54 mm thickness and standard weight, schedule 40 equivalent to a 3.91 mm thickness) and two bend radii (long and short) were chosen. The component identification and relevant dimensions of the elbows are given in Table1 The elbow material used conform to the ASTM specification commonly used in power plant piping. This is A403 WP 304L for austenitic steels. The elbow mechanical properties should in practice conform with the specifications (A312 TP304L) of the straight pipe. The mechanical properties of elbows (A312 TP304L) is given in Table2 Firstly
Table 1. Component identification and geometry (stainless steel) [8] .
*Components are labelled by a four-character coding: First character: S for stainless steel; Second character: L for long or S for short radius bends; Third character: S for standard weight or X for extra strong; Fourth character: 0 is used here to denote out-of-plane bendingme.
Table 2. Material (stainless steel) properties obtained by tensile tests.
the test components were pressurized independently to their design pressure, calculated using the ASME Code formula. The internal pressure was closely monitored and kept constant during testing. The frequency and design pressure of elbows is given in Table3 A pure out-of-plane bending moment applied at one end of a 90˚ welding elbow is reacted by a purely torsional moment at the other end. For the case of 90˚ welding elbows, the recognized mechanism of elastic deformation under pure out-of-plane bending is shown in Figure 1 [8] .
5. Finite Element Arrangement
To understand the general rule of ratcheting behaviour of pressurized piping, the experimental investigation has been researched and valuable results have been obtained. In the experimental conditions, it should be noticed that the structure size and loading conditions are limited. For the design of actual complex structures, FEA can be helpful to predict the ratcheting behavior of pressurized piping based on appropriate constitutive models. ABAQUS is one of the most famous finite element programs that used for structural response simulation under cyclic loading. Advanced constitutive model has been incorporated into ABAQUS. In this study, for all specimens the finite element code, ABAQUS, was used to study ratcheting behavior of pressurized elbows under dynamic moments. Type of elements used in the FE analysis is C3D8R. Number of elements used in the middle part of model and lateral are 1891 and 427 elements, respectively.
The nonlinear constitutive model used in the FEM analyses in this study is derived from formulations by Armstrong and Frederick. It is recommended that the model be calibrated with experimental data that is close to the expected strain range and loading history of the application. Stress-strain data is obtained from several stabilized cycles of specimens that are subjected to symmetric strain cycles. The material parameters 
and 
determine the kinematic hardening component of the model. Three different ways of providing data for the kinematic hardening component of the mode can be given: using half-cycle test data, using single stabilized cycle, or test data obtained from several stabilized cycles. Stress-strain data can be obtained from several stabilized cycles of specimens that are subjected to symmetric strain cycles.
The calibration procedure consists of several cylindrical bar tests, one of which subjected to monotonic tension until necking and others were under symmetric strain-controlled experiments with different strains. During these calibration tests, the stress state must remain uniaxial.
From symmetric strain-controlled experiments, the equivalent plastic strain equals the summation of the absolute value of the change in longitudinal plastic strains:
(3)
where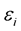 
total strain, 
is the measured stress and E is the elastic modulus.
The equivalent back stress, 
, equals one-half of the difference in yield stress between the end of the tensile loading and first yield of the subsequent compressive loading.
Table 3. The frequency and design pressure.
Figure 1. Cross-section distortion of elbow under out-of-plane bending moment [8] .
These results, corresponding 
data pairs may be plotted, and the kinematic hardening parameters,
and
, may be calculated by fitting Equation (2) to the data and selecting parameters minimize the sum of the square of the error between Equation (2) and the data [
,
].
6. Experimental and FE Results
Detailed results will be presented for four of the specimens (SLSO, SLXO, SSSO and SSXO) and summary results will be given for all specimens conducted. Typical strain response in presence of ratcheting in FE results are shown in Figure 2. Ovalization, instead of occurring, as in the in-plane case, at the intrados/extrados and elbow crown (position defined by ϕ = 0, 180˚), occurs at angular positions ±45˚ from the crown. The positions of maximum stress under out-of-plane bending moments, are the positions located at angles of ±45˚ along the mid-circumference from the elbow faces (crown). This confirms that, for pressurized 90˚ welding elbows under out-of-plane bending, the maximum strains occur midway along the circumference between the crown and intrados/extrados and their directions are along axes orientated at 90˚ between the hoop and axial directions. These strains are presented against measured response moment data and also against response moment data normalized with respect to the limit moment of the components. These are shown in Figure 3 and Figure 4 for the stainless steel components. It is noted from these four figures that the strain accumulation rises rapidly once initiated. Complete set of data for specimens SLSO is presented in Table4
7. Discussion
Results on four pairs of stainless steel, long and short radius piping elbows with two different thicknesses have been presented. The components were subjected to steady internal pressure and resonant, dynamic out-of-plane bending moments. The cyclic strain accumulation as a function of geometry and load level was assessed for all components. This paper, reviews the experimental observations and the FEA results of the structural ratcheting. Experimental and simulation results show that cyclic bending of elbows induces cyclic strain accumulation. The direction of maximum strain is at about 45˚ between the hoop and axial directions. Also, the direction of highest ratcheting was along the hoop direction rather than the direction of maximum principal strain. For all components, the cyclic strain accumulation was found to increase rapidly, once initiated. Typical data obtained ex-
Figure 2. Typical strain response in presence of ratcheting in FE results for specimen SLSO at a dynamic bending moment of 5603.
(a) (b)
Figure 3. (a) Experimental ratcheting data [8] and (b) FE analysis against moment levels for stainless steel.
perimentally and from FE model for specimens SLSO, SLXO, SSSO and SSXO are shown in Figure 3, Figure 4. The experimental and FE results illustrated by Figure 3 & Figure 4 show the onset of hoop ratcheting of pressurized elbows under out-of-plane bending for stainless steel elbows occur at moments of about 0.6 - 0.7 the limit moment.
8. Conclusion
The important conclusion of this paper is to show the properties of nonlinear kinematic hardening model to predict the cyclic loading behavior of the structures. In this study, stress-strain data and material parameters have been obtained from several stabilized cycles of specimens that are subjected to symmetric strain cycles. Both
Table 4 . Experimental and FE ratcheting data for specimen SLSO.
(a) (b)
Figure 4. (a) Experimental ratcheting data [8] and (b) FE analysis against moment levels for stainless steel.
experimental results and the FE analysis agree that ratcheting is influenced by the material stress-strain curve and load history. The rate of ratcheting depends significantly on the magnitude of the internal pressure, dynamic bending moment and material constants for nonlinear kinematic hardening model. The results show that the initial rate of ratcheting is large and then it decreases with the increasing cycles. The FE model predicts the strain ratcheting rate to be near that found experimentally in all cases that
. Otherwise, the results show that the FE method gives over estimated values comparing with the experimental data.
Acknowledgements
Appreciation is expressed to the technical staff of the Applied Mechanics Division of the Department of Mechanical Engineering at the University of Mohaghegh Ardabili (Iran) for their assistance with the work.
Notation
: Pipe Thickness
: Pipe mean radius
: Young’s modulus
: Applied dynamic moment
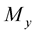: Yield strength
: Elbow limit moment under out-of-plane bending
: Allowable design stress intensity
: Ultimate strength
: Yield strength
: Bend characteristic = tR/r2
: Back stress tensor
: Back stress deviatoric tensor
: Initial size of the yield surface
: Materials constants for kinematic hardening
: Plastic strain tensor
: Equivalent plastic strain
: Angular position around the circumference of the bend (=0˚ at the crown)
: Test natural frequency
NOTES
*Corresponding author.