1. Introduction
In many developed countries skill-selective admission policies are viewed as an effective way to take advantage of the migration they face. The more skilled the migrants, the more they contribute to tax revenues, and the less they depend on government subsidies in the destination country. Moreover, in admitting skilled immigrants, policymakers address the concerns of the less skilled natives who are the most affected by migration flows [1] . Despite the advantages of skill selection, the actual adoption of this strategy remains low [2] . To explain the low extent of skill-selective immigration policies, Facchini and Mayda [3] point out two possible arguments. On the one hand, pressure groups could affect immigration policies, as was the case of the American Medical Association discussed by Bhagwati and Hanson [4] . On the other hand, immigrants entry through the family reunification channel creates uncertainty on the expected flow of migration. Therefore, policymakers are cautious about increasing the number of skilled migrants as they do not want to inflate the total number of migrants.
In this paper, we propose a different explanation of the phenomenon by analyzing the role of illegal immigration flows induced by a shift towards a more selective immigration policy.1 The theoretical model we propose is related to the theory put forward by Magris and Russo [5] , who analyze selective immigration policies from the point of view of fiscal revenues for the government of the destination country.2 Our approach is however different from the theory of immigration amnesties developed by these authors. In our model, there are different types of candidate migrants ranked by their skill level and they are assumed to prefer to be legal rather than illegal. Some of them will be accepted legally and the remaining will try to migrate clandestinely with a given probability of success. We show that an increasingly selective immigration policy can be detrimental for destination countries, as it could imply more illegal immigration flows. We derive the optimal quotas of legal migration for each type of candidate migrants: on the one hand, more legal immigration increases the fiscal basis, on the other one, such a policy decreases the burden of illegal migration, through a mechanism of substitution. In addition, we prove that, under mild hypotheses, an increase in the probability of entering clandestinely implies an increase in the number of legal migrants, that is a less selective immigration policy. In fact, by dislocating some migrants from the informal sector to the formal one, the consequence is that this policy will increase the fiscal base with a mitigate effect on the total number of migrants.
2. The Model
Consider migration flows from the origin country  to the destination country
to the destination country . We assume that the migration flows from the country
. We assume that the migration flows from the country  to country
to country  are mainly explained by wages differential between the two countries.3 Therefore, wages in the destination country are higher than those in the origin country. There are
are mainly explained by wages differential between the two countries.3 Therefore, wages in the destination country are higher than those in the origin country. There are  types of candidate migrants from country
types of candidate migrants from country , ranked by their skills. Let
, ranked by their skills. Let  be the number of type
be the number of type 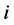 migrants, with
migrants, with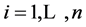 .
.  is the human capital of type
is the human capital of type  migrants. Suppose that
migrants. Suppose that
 (1)
(1)
and denote by  the quota of type
the quota of type  migrants allowed to enter into
migrants allowed to enter into  legally. We assume a constant return to scale technology of the type
legally. We assume a constant return to scale technology of the type , where
, where  is the production made possible by type
is the production made possible by type  migrant. Hence, each type
migrant. Hence, each type  of migrants, whether or not legal are they, receives a wage which is equal to his skill level
of migrants, whether or not legal are they, receives a wage which is equal to his skill level . The government applies a flat tax
. The government applies a flat tax  on the wage of each legal migrant and collects aggregate income taxes
on the wage of each legal migrant and collects aggregate income taxes .4 The government of the destination country
.4 The government of the destination country  is interested in selecting migrants who are able to enlarge sufficiently the fiscal basis. This is done in order to devote more resources to other objectives improving the welfare of the natives. We assume that government of country
is interested in selecting migrants who are able to enlarge sufficiently the fiscal basis. This is done in order to devote more resources to other objectives improving the welfare of the natives. We assume that government of country  has an aversion toward immigrants which assumes the form of a quadratic disutility function:
has an aversion toward immigrants which assumes the form of a quadratic disutility function:
 (2)
(2)
where  is the share of non-selected candidate migrants to enter the country
is the share of non-selected candidate migrants to enter the country  and who cross nevertheless successfully the border illegally. For the sake of simplicity, we assume that
and who cross nevertheless successfully the border illegally. For the sake of simplicity, we assume that  is the same value for each type of migrants, that we will denote
is the same value for each type of migrants, that we will denote . Being an illegal migrant implies some costs. Let
. Being an illegal migrant implies some costs. Let 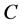 represents any type of costs related to illegal work. It is only when migrants are denied the right to enter legally into the country
represents any type of costs related to illegal work. It is only when migrants are denied the right to enter legally into the country  that they choose to hide. We assume that crossing the border legally is the first best for migrants, i.e.
that they choose to hide. We assume that crossing the border legally is the first best for migrants, i.e.
 (3)
(3)
At the same time, we assume that the utility  deriving from remaining in the
deriving from remaining in the  country is lower than the one a clandestine derives from a successful migration, legal or illegal, i.e. for each
country is lower than the one a clandestine derives from a successful migration, legal or illegal, i.e. for each , one has:
, one has:
 (4)
(4)
Under Conditions (3) and (4), all individuals in country  will try to migrate to
will try to migrate to . The first and second terms into the parenthesis of (2) express the opposition of natives towards legal and illegal migration flows, respectively. There are several reasons that explain natives attitude towards immigration. To mention only the economic arguments, Hanson, Scheve, and Slaughter [7] show that the less favorable US natives to immigration are those who live in states with a large population of migrants and with generous public goods provided to migrants. Facchini and Mayda [8] find a negative correlation between individual income and pro-immigration preferences when countries face a low skilled flow of migrants. Epstein and Weiss [9] mention several arguments that may explain why illegal immigrants are more costly to a country and therefore less desired by natives. One main argument is that illegal immigrants consume public resources without paying taxes and may increase social costs, if involved in crimes.
. The first and second terms into the parenthesis of (2) express the opposition of natives towards legal and illegal migration flows, respectively. There are several reasons that explain natives attitude towards immigration. To mention only the economic arguments, Hanson, Scheve, and Slaughter [7] show that the less favorable US natives to immigration are those who live in states with a large population of migrants and with generous public goods provided to migrants. Facchini and Mayda [8] find a negative correlation between individual income and pro-immigration preferences when countries face a low skilled flow of migrants. Epstein and Weiss [9] mention several arguments that may explain why illegal immigrants are more costly to a country and therefore less desired by natives. One main argument is that illegal immigrants consume public resources without paying taxes and may increase social costs, if involved in crimes.
3. The Optimal System of Quotas
In view of the above considerations, the problem of the government consists in choosing a vector  which maximizes total utility
which maximizes total utility , i.e.:
, i.e.:
 (5)
(5)
Following analogous lines as in Magris and Russo [5] , we are able to solve the maximization program of the government and to show a proposition which provides a characterization of the optimal share of legal migrants. The solution turns out to be intuitive once one recalls to mind that a more generous system of quotas will dislocate some potential illegal immigrants from the informal sector to the formal one, where individuals pay income taxes. Therefore the incentive of increasing legal migration is twofold: on the one hand, this policy increases the fiscal basis; on the other hand, the effect on total migration is mitigate since only a fraction q of those whose legal entry is denied will join the informal sector.
Proposition 1 The solution of the maximization problem (5) is such that there exists a 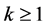 satisfying:
satisfying:
 (6)
(6)
Proof. Taking the partial derivatives of (5) with respect to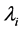 ,
,  , we get:
, we get:

Notice that at most one derivative  can be equal to zero and the second order conditions are verified since the objective function is strictly concave. If, for example,
can be equal to zero and the second order conditions are verified since the objective function is strictly concave. If, for example,  , this entails that
, this entails that . This is impossible insofar as inequalities (1) do hold. If we observe that
. This is impossible insofar as inequalities (1) do hold. If we observe that  for some
for some , we deduct that
, we deduct that  for all
for all  and
and  for
for . To show this, suppose for example
. To show this, suppose for example . Then, we get:
. Then, we get:
 (7)
(7)
If we substitute (7) into R1, we get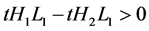 . By substituting into R3, we obtain
. By substituting into R3, we obtain , and so on. We provide hereafter the details of the optimization solution. Consider the derivative
, and so on. We provide hereafter the details of the optimization solution. Consider the derivative  evaluated at
evaluated at . If
. If , we get
, we get 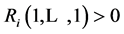 for any
for any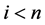 , and the solution is
, and the solution is
 . If
. If , we look if there exists a
, we look if there exists a  such that
such that  evaluated at
evaluated at
 is equal to zero. If the answer is positive, then the solution of the maximization problem will be
is equal to zero. If the answer is positive, then the solution of the maximization problem will be . Conversely, if
. Conversely, if 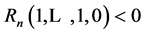 we look at
we look at : if it is positive or equal to zero, then the solution will be
: if it is positive or equal to zero, then the solution will be . If
. If , we look if there exists a
, we look if there exists a  such that
such that  evaluated at
evaluated at  is equal to zero. If the answer is positive, then the solution of the maximization problem will be
is equal to zero. If the answer is positive, then the solution of the maximization problem will be . On the contrary, if
. On the contrary, if 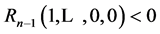 we look at
we look at . We therefore iterate this procedure until we find a
. We therefore iterate this procedure until we find a
 such that
such that , with
, with , and the optimal solution will be
, and the optimal solution will be
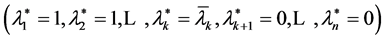 . Finally it is immediate to verify that, if
. Finally it is immediate to verify that, if , the solution will be
, the solution will be 
In view of the proposition mentioned above, one may wonder how the government would react if the probability of a successful illegal immigration would increase. To understand what happens, suppose that the solution of the maximization problem entails a  such that
such that  with
with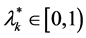 . The corresponding marginal utility of the government is:
. The corresponding marginal utility of the government is:
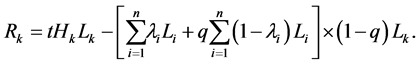
Taking the total derivative of  with respect to
with respect to  and
and , we get:
, we get:
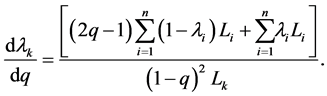 (8)
(8)
The Equation (8) fulfills the condition  when
when . When Equation (8) is satisfied, an increase in the share of migrants that cross the border illegally will force the government to change its policy and become less selective. This is due to the fact that when the probability to become clandestine is larger, an higher share of accepted migrants will not strongly increase the total number of migrants established in the country.
. When Equation (8) is satisfied, an increase in the share of migrants that cross the border illegally will force the government to change its policy and become less selective. This is due to the fact that when the probability to become clandestine is larger, an higher share of accepted migrants will not strongly increase the total number of migrants established in the country.
4. Conclusion
Rich countries view their welfare as being served, on the one hand, by selecting skilled would-be migrants and, on the other hand, by keeping illegal migrants away. Our analyses reveal that there can be a conflict between these two objectives. By adopting a more selective immigration policy, rich countries run the risk of attracting more illegal migrants. Put differently, flexible skill immigration policies reflect the fear of countries to face more illegal migrants flows. Undoubtedly, selective immigration policies are coupled with external enforcement (border controls and deportations) and internal enforcement (work site raids and employer sanctions) to cope with illegal immigration. One can therefore object that tougher skill selectivity triggers more illegal migration. However, border controls lead to the mobilization of substantial financial resources and, in the US case, the results of these policies are mixed. Record increases in border enforcement have failed to stop illegal immigration. The net flow of undocumented immigrants into the USA average over 500,000 per year and an estimated 11.5 million unauthorized immigrants had been living in the USA in January 2011 [10] [11] . The estimated probability of apprehension is 23.6 percent for migrants to the United States and 5.7 percent for Spain [12] . Increasing border and internal control expenditures can have negative effects on countries. Djajic [13] argued that efforts to control illegal immigration may trigger networks supporting clandestine foreign workers so that the result may be an increase in the overall stock of illegal immigrants. Myers and Papageorgiou [14] show that higher costs of border control lead the rich country to allow some immigration in order to reduce expenditures on border control. They also find that inequality in the rich country increases as border control becomes more expansive. In so far as illegal migrants are more costly to a country than the legal ones, this paper shows that it is in the interest of countries to adopt flexible skill policy. In our model, we show that less selective immigration policies can entail a positive effect for the destination country: they actually increase the fiscal revenue with, at the same time, a mitigate effect on total migration, since only a share of those who are denied to enter legally convert themselves into illegal workers, being the probability of joining the informal sector lower than one.
Acknowledgments
We are greatly indebted to Francesca Busetto for helpful comments and suggestions that improved the paper. We also thank Rémi Bazillier and Patrick Villieu for their suggestions.
NOTES
*Corresponding author.

1More illegal immigration as a response to a more restrictive immigration policies is not unlikely. A historical example is the end of the Bracero Program (1942-1964) which induced a large scale illegal entry in the United States.
2Hatton shows that the attitude towards immigration is determined to a greater extent by concerns about public finances and social spending than by concerns about the labor market.
3Demographic changes in the origin countries, immigration policies, networks are some non-wage factors that can explain the choice to migrate.
4Admittedly, natives also pay taxes. We are interested in migrants participation to fiscal revenues.