1. Introduction
In 2009, the idea of general integral control, which uses all available state variables to design the integrator, firstly was proposed by [1] , which presented some general integrators and controllers. However, their justification was not verified by mathematical analysis. In 2012, general integral control design based on linear system theory was presented by [2] , where the linear combination of all the states of dynamics was used as the integrator.
The results, however, were local. The regional as well as semi-global results were proposed in [3] , where the sliding mode manifold was used as the integrator, and then general integral control design was achieved by using sliding mode technique and linear system theory. In 2013, a class of nonlinear integrator, which was shaped by diffeomorphism, was proposed by [4] , where feedback linearization technique was used to analyze the closed-loop system stability. General concave integral control was proposed in [5] , where a class of concave function gain integrator is presented and the partial derivative of Lyapunov function is introduced into the integrator design. In consideration of the twinning of the concave and convex concepts, general convex integral control was proposed by [6] , where the method to design the convex function gain integrator is presented and its highlight point is that the integral control action seems to be infinity but its factually is finite in time domain. Although general concave and convex integral control are all bounded integral control, one major limitation of them is that the indispensable element of the integrator is limited to the partial derivative of Lyapunov function, another is the function sets, which are used to design the general concave and convex integrator and integral control action, only were limited to two kinds of function sets. These two limitations become a serious obstruction to design a high performance integral controller. In addition, the generalization of the integrator and integral control action, which is achieved by defining two function sets, respectively, was proposed by [7] , and its one drawback is that the integral control action could tend to infinity.
In consideration of the limitation of general concave and convex integral control, the aim of this paper is to propose a systematic and more generic method to construct general bounded integral control such that for a particular application, the control engineers not only can choose the most appropriate control law in hand but also have more freedom to construct the bounded integral control action and integrator. The main contributions are as follows: 1) three new function sets are defined, respectively; 2) three kinds of method to construct general bounded integral control action and integrator are proposed; 3) the indispensable element used to construct the integrator is not confined to the partial derivative of Lyapunov function [5] [6] and function set [7] , which is used to construct the integrator, and can be taken as any integrable function, which satisfies Lipschitz condition and the self excited integral dynamic is asymptotically stable; 4) the function sets used to construct the bounded integral control action have a wider range of choice than the corresponding function sets proposed by [5] -[7] ; 5) a class of positive define bounded gain function is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the control performance; 6) exact knowledge of Lyapunov function is not necessary and it only needs to satisfy some bounded information; 7) by using Lyapunov method and LaSalle’s invariance principle, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established. As a result, the generalization of the bounded integral control is achieved.
Throughout this paper, we use the notation  and
and  to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix
to indicate the smallest and largest eigenvalues, respectively, of a symmetric positive define bounded matrix , for any
, for any . The norm of vector
. The norm of vector
 is defined as
is defined as , and that of matrix
, and that of matrix  is defined as the corresponding induced norm
is defined as the corresponding induced norm  .
.
The remainder of the paper is organized as follows. Section 2 describes the system under consideration, assumption, definition and proof of Lemma. Section 3 addresses the method to construct general bounded integral control. Conclusions are presented in Section 4.
2. Problem Formulation
Consider the following nonlinear system,
 (1)
(1)
where  is the state,
is the state,  is the control input,
is the control input,  is the controlled output,
is the controlled output,  is a vector of unknown constant parameters and disturbances. The function
is a vector of unknown constant parameters and disturbances. The function ,
,  and
and  are continuous in
are continuous in  on the whole control domain
on the whole control domain . Let
. Let  be a vector of constant reference. Set
be a vector of constant reference. Set  and
and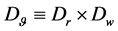 . We want to design a feedback control law
. We want to design a feedback control law  such that
such that  as
as .
.
Assumption 1: For each , there is a unique pair
, there is a unique pair  that depends continuously on
that depends continuously on 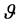 and satisfies the equations,
and satisfies the equations,
 (2)
(2)
so that  is the desired equilibrium point and
is the desired equilibrium point and  is the steady-state control that is needed to maintain equilibrium at
is the steady-state control that is needed to maintain equilibrium at , where
, where .
.
No loss of generality, we state all definitions, theorems and assumptions for the case when the equilibrium point is at the origin of , that is,
, that is, .
.
Assumption 2: No loss of generality, suppose that the function  satisfies the following inequalities,
satisfies the following inequalities,
 (3)
(3)
 (4)
(4)
where  is a positive constant.
is a positive constant.
Assumption 3: Suppose that there exists a control law  such that
such that  is an exponentially stable equilibrium point of the system (5) and the inequality (6) hold,
is an exponentially stable equilibrium point of the system (5) and the inequality (6) hold,
 (5)
(5)
 (6)
(6)
and there exists a Lyapunov function  such that the following inequlities,
such that the following inequlities,
 (7)
(7)
 (8)
(8)
 (9)
(9)
hold for all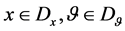 , where
, where  and
and  are all positive constants.
are all positive constants.
For the purpose of this paper, it is convenient to introduce the following definitions and Lemmas. For the convenient comparison with the general concave and convex integral control, it is necessary to explain that the following Definition 1 and 2 was proposed by reference [5] [6] , respectively.
Definition 1: 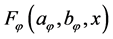 with
with  and
and  denotes the set of all continuous differential increasing bounded functions [5] [8] ,
denotes the set of all continuous differential increasing bounded functions [5] [8] ,

such that
 ,
,
 ,
, 
 ,
, 
 .
.
where  stands for the absolute value.
stands for the absolute value.
Figure 1 depicts the region allowed for one component of functions belonging to function set . For instance, for all
. For instance, for all , hyperbolic tangent function, arc tangent function, Amosin function [8] and so on, all belong to function set
, hyperbolic tangent function, arc tangent function, Amosin function [8] and so on, all belong to function set .
.
Definition 2:  with
with  and
and , denotes the set of all continuous differential increasing functions [6] ,
, denotes the set of all continuous differential increasing functions [6] ,


Figure 1. The region allowed for one component of functions belonging to function set .
.
such that
 ,
,

and given any , there exists a positive constant
, there exists a positive constant  such that
such that
 .
.
where  stands for the absolute value.
stands for the absolute value.
Figure 2 describes an example curve and the region allowed for the derivative reciprocal of one component of functions belonging to function set . For instance, for all
. For instance, for all , the functions,
, the functions,  ,
,  ,
,  and so on, all belong to function set
and so on, all belong to function set .
.
Definition 3:  with
with , and
, and  denotes the set of all continuous differential increasing functions,
denotes the set of all continuous differential increasing functions,

such that
 ,
,

 .
.
Figure 3 depicts the example curves for one component of functions belonging to function set . For instance, for all
. For instance, for all , the functions,
, the functions,  with
with  and
and ,
,  , and so on, all belong to function set
, and so on, all belong to function set .
.
Definition 4:  with
with  and
and  denotes the set of all continuous positive define bounded functions,
denotes the set of all continuous positive define bounded functions,

such that
 and given any
and given any , there exists
, there exists  such that
such that
 .
.
Figure 4 depicts the example curves and the region allowed for one component of functions belonging to

Figure 2. Example curve and the region allowed for the derivative reciprocal of one component of functions belonging to function set .
.

Figure 3. Example curves of functions belonging to function set .
.

Figure 4. Example curves and the region allowed for one component of functions belonging to function set .
.
function set . For instance, for all
. For instance, for all , the functions,
, the functions,  , and so on, all belong to function set
, and so on, all belong to function set .
.
Definition 5:  with
with 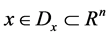 denotes the set of all integrable functions,
denotes the set of all integrable functions,

such that
 ,
,
 is an asymptotically stable equilibrium point of the self excited integral dynamic
is an asymptotically stable equilibrium point of the self excited integral dynamic
 for all
for all .
.
where  is a positive constant. For instance, for all
is a positive constant. For instance, for all , the functions,
, the functions,  and so on, all belong to function set
and so on, all belong to function set .
.
Lemma 1: Let  or
or  with
with  or
or , and then the function [6] ,
, and then the function [6] ,

is a positive define bounded increasing function, that is,  for all
for all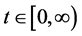 , where
, where  is the limit of
is the limit of  as
as . Its proof consults the reference [6] .
. Its proof consults the reference [6] .
Lemma 2: Let  or
or  with
with ,
,  and
and , and then the function,
, and then the function,

is bounded, that is,  for all
for all  and
and , where
, where  is a positive constant.
is a positive constant.
Proof: by definition of  and Definition 5, we have,
and Definition 5, we have,

Now, using Lemma 1, we obtain,
 .
.
Thus,  is bounded, that is,
is bounded, that is,  for all
for all  and
and .
.
Discussion 1: Comparing the two function sets  and
and  proposed by [5] [6] with the function set
proposed by [5] [6] with the function set , it is no hard to see that although they all claim that the function is continuous differential increasing function, the main differences are as follows: the limiting conditions of the function set
, it is no hard to see that although they all claim that the function is continuous differential increasing function, the main differences are as follows: the limiting conditions of the function set  is less than the function sets
is less than the function sets  and
and . Thus, the function set
. Thus, the function set  can completely includes the any functions belonging to the two function sets
can completely includes the any functions belonging to the two function sets  and
and .
.
Discussion 2: Comparing the function set [7] , which was used to generalize the integral control action, with the function set , the differences are the limiting condition about their derivatives, that is, the former demands
, the differences are the limiting condition about their derivatives, that is, the former demands  (
( ,
, and
and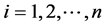 ). However, the latter only requires
). However, the latter only requires
 . Thus, the function set
. Thus, the function set  not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set
not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set  have a wider range of choice than the one proposed by [7] .
have a wider range of choice than the one proposed by [7] .
Discussion 3: Comparing the function set [7] , which was used to generalize the integrator, with the function set , the differences are that: the former is defined by resorting to Mean Value Theorem, therefore, it requires that the function is differential. However, the latter is defined by designing a self excited integral dynamic, and only demands its origin is asymptotically stable, and then differentiability condition is removed. Thus, it is not hard to see that the function set
, the differences are that: the former is defined by resorting to Mean Value Theorem, therefore, it requires that the function is differential. However, the latter is defined by designing a self excited integral dynamic, and only demands its origin is asymptotically stable, and then differentiability condition is removed. Thus, it is not hard to see that the function set  not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set
not only can completely include the any functions belonging to the function set proposed by [7] but also the functions belonging to the function set  have a wider range of choice than the one proposed by [7] .
have a wider range of choice than the one proposed by [7] .
Discussion 4: It is obvious that the bound of function,  , which is obtained by Lemma 2, is too conservative and even is not of interest. The situation, however, is not as bad as it might seem. As shown by Figure 2 and Figure 3, we can use
, which is obtained by Lemma 2, is too conservative and even is not of interest. The situation, however, is not as bad as it might seem. As shown by Figure 2 and Figure 3, we can use  or
or  as its approximate value in practice, corresponding to
as its approximate value in practice, corresponding to  small enough.
small enough.
3. Constructive Method
In general, integral controller comprises three components: the stabilizing controller, integral control action and integrator. Thus, a general integral controller can be given as,
 (10)
(10)
where
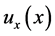 is an ordinary control law;
is an ordinary control law;
 is a positive define diagonal matrix;
is a positive define diagonal matrix;
 is a continuous differential increasing function with
is a continuous differential increasing function with ;
;
 is a positive constant vector or positive define vector function;
is a positive constant vector or positive define vector function;
 belongs to function set
belongs to function set ;
;
 .
.
Thus, substituting (10) into (1), obtain,
 (11)
(11)
By Assumption 1 and choosing  to be nonsingular and large enough, and then set
to be nonsingular and large enough, and then set  and
and  of (11), obtain,
of (11), obtain,
 (12)
(12)
Therefore, we ensure that there is a unique solution, 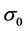 , and then
, and then  is a unique equilibrium point of the closed-loop system (11) in the control domain of interest. At the equilibrium point,
is a unique equilibrium point of the closed-loop system (11) in the control domain of interest. At the equilibrium point,  , irrespective of the value of
, irrespective of the value of .
.
Now, the design task is to provide methods to construct the bounded integral control action and integrator in the control law (10) such that  is bounded and
is bounded and  is an asymptotically stable equilibrium point of the closed-loop system (11) in the control domain of interest. To achieve this objective, the methods can be summarized as follows:
is an asymptotically stable equilibrium point of the closed-loop system (11) in the control domain of interest. To achieve this objective, the methods can be summarized as follows:
Method 1: If we choose , and then by definition of
, and then by definition of , it is easy to know that the integral control action is bounded for all
, it is easy to know that the integral control action is bounded for all . Thus,
. Thus,  can be taken as any positive define bounded vector function or positive constant vector, that is,
can be taken as any positive define bounded vector function or positive constant vector, that is,  with
with  and
and . Consequently, we have,
. Consequently, we have,
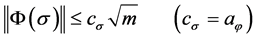 , and
, and
 .
.
As a result, the generalization of the general concave integral control is achieved.
Method 2: If we choose , and then design
, and then design  such that
such that
 ,
,
 , and
, and

hold for all  and
and . Thus, by Lemma 1 and 2, it is easy to know that this kind of integral control action is bounded in time domain, that is,
. Thus, by Lemma 1 and 2, it is easy to know that this kind of integral control action is bounded in time domain, that is,

where
 ,
,
 ,
,
 , and
, and
 .
.
As a result, the generalization of the general convex integral control is achieved.
Method 3: If we choose , constructive general bounded integral control can be divided into two cases: 1) if
, constructive general bounded integral control can be divided into two cases: 1) if  is bounded, and then
is bounded, and then  can be taken as any positive define bounded vector function or positive constant vector. The condition for
can be taken as any positive define bounded vector function or positive constant vector. The condition for  is the same as Method 1; 2) if
is the same as Method 1; 2) if  is unbounded for all
is unbounded for all , and then
, and then  needs to be designed like Method 2. The condition for
needs to be designed like Method 2. The condition for  is the same as Method 2. It is obvious that this is a more generic method to construct general bounded integral control because the function set used to construct the bounded integral control action has a wider range of choice than the corresponding function sets proposed by [5] -[7] . Moreover, it is worth noting that
is the same as Method 2. It is obvious that this is a more generic method to construct general bounded integral control because the function set used to construct the bounded integral control action has a wider range of choice than the corresponding function sets proposed by [5] -[7] . Moreover, it is worth noting that  can be designed like Method 2 when
can be designed like Method 2 when  is bounded.
is bounded.
In addition, it is convenient to introduce the variable,  , which is equal to
, which is equal to ,
,  and
and , respectively, corresponding to the above three kinds of choices of the function
, respectively, corresponding to the above three kinds of choices of the function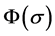 .
.
Based on the control law  and three kinds of integral control actions and integrators above, the following theorem can be established.
and three kinds of integral control actions and integrators above, the following theorem can be established.
Theorem 1: Under Assumptions 1 - 3, if there exists a positive define diagonal matrix 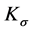 such that the following inequality,
such that the following inequality,
 (13)
(13)
and the inequality (20) hold, and then  is an exponentially stable equilibrium point of the closed-loop system (11). Moreover, if all assumptions hold globally, and then it is globally exponentially stable.
is an exponentially stable equilibrium point of the closed-loop system (11). Moreover, if all assumptions hold globally, and then it is globally exponentially stable.
Proof: To carry out the stability analysis, we consider the following Lyapunov function candidate,
 (14)
(14)
where
 ,
,  ,
,
 is a positive define
is a positive define  matrix;
matrix;
 is a
is a  matrix;
matrix;  is a
is a  matrix;
matrix;
 is a
is a  matrix,
matrix,  ,
, .
.
Obviously, Lyapunov function candidate (14) is positive define. Therefore, our task is to show that its time derivative along the trajectories of the closed-loop system (11) is negative define, which is given by,
 (15)
(15)
Substituting (12) into (11), we obtain,
 (16)
(16)
Now, by the above three kinds of choices of the function , we have,
, we have,
 (17)
(17)
Substituting (16) into (15), and using (3), (4), (6), (8), (9), (17) and , we obtain,
, we obtain,
 (18)
(18)
where

 and
and
 .
.
and then inequality (18) can be rewritten as,
 (19)
(19)
where
 ,
, .
.
The right-hand side of the inequality (19) is a quadratic form, which is negative define when
 (20)
(20)
Using the fact that Lyapunov function (14) is a positive define function and its time derivative is a negative define function if the inequalities (13) and (20) hold, we conclude that the closed-loop system (11) is stable. In fact,  means
means  and
and . By invoking LaSalle’s invariance principle [9] , it is easy to know that the closed-loop system (11) is asymptotically stable.
. By invoking LaSalle’s invariance principle [9] , it is easy to know that the closed-loop system (11) is asymptotically stable.
Discussion 5: Compared to general convex and concave integral control [5] [6] , it is easy to see that this paper is not a simple extension of them but proposes a systematic and more generic method to construct general bounded integral control. The main progresses are as follows: 1) the indispensable element  used to construct the integrator can be taken any functions belonging to function set
used to construct the integrator can be taken any functions belonging to function set  and is not confined to the partial derivative of Lyapunov function
and is not confined to the partial derivative of Lyapunov function , which is used to construct the integrator in [5] [6] ; 2) a positive define bounded gain function
, which is used to construct the integrator in [5] [6] ; 2) a positive define bounded gain function  is introduced into the integrator, which can be used to improve the integral control performance; 3) a class of new function set
is introduced into the integrator, which can be used to improve the integral control performance; 3) a class of new function set  is defined, and then the method to construct general bounded integral control action and integrator is extended to a wider function set
is defined, and then the method to construct general bounded integral control action and integrator is extended to a wider function set . As a result, this is a fire new and more generic method to construct general bounded integral control action and integrator; 4) we need not exact knowledge of Lyapunov function
. As a result, this is a fire new and more generic method to construct general bounded integral control action and integrator; 4) we need not exact knowledge of Lyapunov function  and only need it satisfy some bounded information. Moreover, if the partial derivative of Lyapunov function is attached into the function
and only need it satisfy some bounded information. Moreover, if the partial derivative of Lyapunov function is attached into the function , the stability conditions can be relaxed. All these mean that the control engineers have more freedom to design the integrator and bounded integral control action, and then a high performance integral controller is more easily found.
, the stability conditions can be relaxed. All these mean that the control engineers have more freedom to design the integrator and bounded integral control action, and then a high performance integral controller is more easily found.
Discussion 6: Compared to the generalization integrator and integral control action proposed by [7] , the main differences are as follows: 1) the integrators proposed by [7] are unattached with the integral control action. However, the integrators presented here are all educed by differentiating the nonlinear function, which is used to produce the integral control action; 2) the integral control actions proposed by [7] could tend to infinity. However, the integral control actions proposed here are all bounded. This means that this kind of integral control can devote its mind to counteract the unknown constant uncertainties and filter out the other action, and then actuator saturation is easy to be removed in practice; 3) a positive define bounded gain function  is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the integral control performance; 4) as mentioned at Discussion 2 and 3, the function sets
is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the integral control performance; 4) as mentioned at Discussion 2 and 3, the function sets  and
and  used to construct the integrator and integral control action, respectively, all have a wider range of choice than the corresponding function sets proposed by [7] .
used to construct the integrator and integral control action, respectively, all have a wider range of choice than the corresponding function sets proposed by [7] .
Remark 1: From the statement above, It is obvious that: First, five function sets for constructing general bounded integral control action is enumerated; Second, three general methods to construct the bounded integral control action are proposed; Final, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established. Under the domination of this theorem, all of them synthesize a systematic and more generic method to construct general bounded integral control together. Consequently, for a particular application, the control engineers not only can choose the most appropriate control law in hand but also have more freedom to design the bounded integral control action and integrator, and then a high performance integral controller is more easily found.
4. Conclusion
This paper is not a simple extension of general convex and concave integral control but proposes a systematic and more generic method to construct general bounded integral control. The main contributions are as follows: 1) three new function sets are defined, respectively; 2) three kinds of method to construct general bounded integral control action and integrator are proposed; 3) the indispensable element used to construct the integrator is not confined to the partial derivative of Lyapunov function [5] [6] and function set [7] , which is used to construct the integrator, and can be taken as any integrable function, which satisfies Lipschitz condition and the self excited integral dynamic is asymptotically stable; 4) the function sets used to construct the bounded integral control action has a wider range of choice than the corresponding function sets proposed by [5] -[7] ; 5) a class of positive define bounded gain function is introduced into the integrator, which provides the designer with additional degrees of freedom to improve the control performance; 6) exact knowledge of Lyapunov function is not necessary and it only needs to satisfy some bounded information; 7) by using Lyapunov method and LaSalle’s invariance principle, a universal theorem to ensure regionally as well as semi-globally asymptotic stability is established. As a result, the generalization of the bounded integral control is achieved.