A New Approach for the Exact Solutions of Nonlinear Equations of Fractional Order via Modified Simple Equation Method ()
1. Introduction
Nonlinear partial differential equations have shown a variety of applications in almost every field of life, such as in electromagnetics, acoustics, electrochemistry, cosmology, biological and material science [1] -[4] . Fractional differential equations can be considered as the general form of the differential equations, as they are involved with the derivatives of any real or complex order (for details see [3] ).
Knowing the importance of differential equations of fractional order, lots of authors are working to find the exact or numerical solutions of the equations. For examples, the adomian decomposition method [5] , Pade approximation method [6] and generalized differential transform method [7] [8] have been used to find the numerical solutions for fractional order differential equations. The 
-expansion method was introduced, by Wang et al. [9] , to find the travelling wave solutions of nonlinear evolution equations. This method was further extended [10] [11] to find the solutions of fractional order differential equations, the Jacobi elliptic function expansion method [12] , the tanh-function method for finding solitary wave solutions [13] , the homotopy perturbation method [14] , the first integral method [15] , the solitary wave ansatz [16] etc.
In this article, a new approach has been developed to find the exact solutions of nonlinear partial differential equations of fractional order by the fractional complex transformation [17] and modified simple equation method [18] [19] , in the sense of modified Riemann-Liouville derivative. For this, we first use the fractional complex transformation on these equations to convert into ordinary differential equations. Then, the modified simple equation method can be applied to find the exact solutions. Two applications are being considered to find the solution of nonlinear Burgers’ equation with time-space fractional derivatives, which has the following form [5] :
(1.1)
and time-spce fractioanl derivative foam drainage equation [11] :
(1.2)
The rest of the article is organized as follows, in section 2 the basic definitions and properties of the fractional theory are considered regrading to modified Riemann-Liouville derivative. In section 3, the modified simple equation method has been proposed to find the exact solutions for NPDEs of fractional order with the help of fractional complex transformation. The two applications are being considered to find the exact solution in section 4. In last section 5, the conclusion has been drawn.
2. Preliminaries and Basic Definitions
In this section, the extended method has been applied in the sense of the Jumarie’s modified Riemann-Liouville derivative of order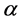
. For this, some basic definitions and properties of the fractional calculus theory are being considered (for details see [3] ). Thus, the fractional integral and derivatives can be defined following [20] [21] :
Definition 2.1 A real function
, is said to be in the space
, if there exists a real number 
such that
, where
, and it is said to be in the space 
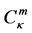if
,
.
Definition 2.2 The Jumarie’s modified Riemann-Liouville derivative, of order
, can be defined by the following expression:
Moreover, some properties for the modified Riemann-Liouville derivative have also been given as follows:
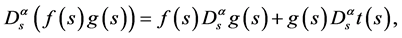
3. The Modified Simple Equation Method
In this section, the modified simple equation method [18] has been discussed to obtain the solutions of nonlinear partial differential equations of fractional order, in very easy way.
For this, we consider the following NPDE of fractional order:
(3.1)
where u is an unknown function and P is a polynomial of u and its partial fractional derivatives along with the involvement of higher order derivatives and nonlinear terms.
To find the exact solutions, the method can be performed using the following steps.
Step 1: First, we convert the NPDE of fractional order into nonlinear ordinary differential equations using fractional complex transformation introduced by Li et al. [17] .
The travelling wave variable
(3.2)
where K, L and M are non-zero arbitrary constants, permits us to reduce Equation (3.2) to an ODE of 
in the following form
(3.3)
Step 2: Suppose that the solution of Equation (3.3) can be expressed as a polynomial of 
in the form:
(3.4)
where 
s are arbitrary constants.
Step 3: The homogeneous balance can be used, to determine the positive integer m, between the highest order derivatives and the nonlinear terms appearing in (3.4).
Step 4: After the substitution of (3.4) into (3.3), we collect all the terms with the same order of 
together. Equate each coefficient of the obtained polynomial to zero, yields the set of algebraic equations for 
and
.
Step 5: After solving the system of algebraic equations, the variety of exact solutions can be celebrated.
4. Applications to the Modified Simple Equation Method
In the following subsections, two applications (given in Equations (1.1) and (1.2)) are being considered to find the exact solutions by the proposed method.
4.1. Nonlinear Time-Space Fractional Burgers’ Equation
In this section, the modified simple equation method has been applied to construct the exact solutions for the nonlinear space-time fractional Burgers’ Equation (1.1). It can be observed that the fractional complex transform
(4.1)
where K and L are constants, permits to reduce the Equation (1.1) into an ODE of the following form:
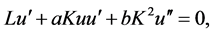(4.2)
Now by calculating the homogeneous balance (i.e.,
), between the highest order derivatives and nonlinear term presented in the above equation, we have the following form
(4.3)
where 
and L are arbitrary constants. To determine these constants substitute the Equation (4.3) into (4.2), and collecting all the terms with the same power of 
and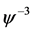 
together, equating each coefficient equal to zero, yields a set of algebraic equations.
(4.4)
(4.5)
and
(4.6)
The above Equation (4.6), yields the value
.
The general solution of the Equation (4.4) is
(4.7)
While 
and 
are arbitrary constants. Consequently to this, the exact solution of the Equation (1.1) has the following form
For, the value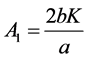 
the Equation (4.5) reduces to
which also gives the same results.
4.2. Nonlinear Time-Space Fractional Derivative Foam Drainage Equation
Applying the fractional complex transformation on the Equation (1.2), which reduces into the following form:
(4.8)
Now by calculating the homogeneous balance, which is
. We have the following form of the Equation (3.4)
(4.9)
where 
and 
are arbitrary constants. To determine these constants, equate the coefficients of
, 
and 
equal to zero, yields the set of algebraic equations.
(4.10)
(4.11)
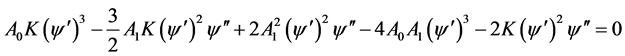(4.12)
and
(4.13)
The above Equation (4.13), yields the value
.
Case 1: The general solution of the Equation (4.10) is
where 
and 
are arbitrary constants. Consequently to this, the exact solution of the Equation (1.2) has the following form
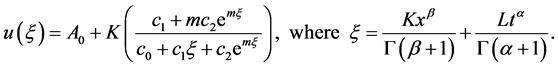
Case 2: For the value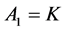
, the general solution of the equation (4.11) is
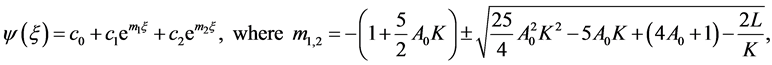
while 
and 
are arbitrary constants. Consequently to this, the exact solution of the Equation (4.1) has the following form
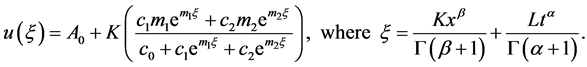
Case 3: For the value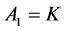
, the general solution of the Equation (4.12) is
where 
and 
are arbitrary constants. Consequently to this, the exact solution of the Equation (1.2) has the following form
Which are the required results.
5. Conclusion
The modified simple equation method has been extended to solve the nonlinear partial differential equation of fractional order, in the sense of modified Riemann-Liouville derivative. First, the fractional complex transformation has been used to convert the fractional order differential equations into ordinary differential equations. Then, the modified simple equation method has been used to find the exact solutions. The two applications have been considered to find the new exact solutions for the nonlinear time-space fractional derivative Burgers’ equation and time-space fractional derivative foam drainage equation. It can also be concluded that the proposed method is very simple, reliable and a variety of exact solutions to NPDEs of fractional order are proposed.