On the Definition of State Variables for an Internal State Variable Constitutive Model Describing Metal Deformation ()
1. Introduction
The author of this paper recently published a textbook entitled “Fundamentals of Strength—Principles, Experiment, and Applications of an Internal State Variable Constitutive Formalism” [1] . Within the constitutive modeling community, the title is self-explanatory and clear. There are many engineers tasked with modeling a deformation process, however, for whom this is not the case. An objective of this paper is to describe the title of this textbook for this broader community. The approach will be to draw an analogy with the most common internal state variable model—the Ideal Gas Law—and to demonstrate how a metal would behave if its deformation behaviors were well-described by an internal state variable model. The fact that the most common constitutive formalisms are shown to fail this test points to the need for an alternate approach. The textbook describes one of these in some detail. This paper is not intended to review the specific model that is the subject of the textbook, but to serve as a complement to the textbook and perhaps ease the use of internal state variable models by a broader community of scientists and engineers.
2. The Ideal Gas Law
High school chemistry students are introduced to the ideal gas law. This law specifies for a gas the relation between the pressure (P, N/m2 or Pa), absolute temperature (T, K), volume (V, m3), and quantity, which is described by the number of moles, n1. The Ideal Gas Law is written
 (1)
(1)
where R is the gas constant which equals 8.314 m3∙Pa/K/mole. Equation (1) is a mathematical representation (a constitutive law) of the “state” of the gas at any instance. State refers to “the totality of macroscopic properties associated with a system” [2] . In Equation (1), P and T are intensive state variables in that they are independent of mass. The volume V, however, is an extensive state variable because it varies with mass. It is convenient to divide the volume by the number of moles giving the specific volume, v (m3/mole), which is an intensive state variable. Equation (1) becomes
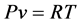 (2)
(2)
The essence of Equation (2) is that the three state variables—T, P, and v—uniquely define the state of the system. Secondly, the path from one state (T1, P1, and v1) to a second state (T2, P2, and v2) is unimportant. This implies “path independence”. To illustrate this, Figure 1 plots P versus v for an ideal gas. The curves identified as “T (K) isotherms” show how P varies with v at various temperatures according to Equation (2). Identified on Figure 1 are an initial state (1) and a final state (4). One could move from (1) to (2) by imposing an increase in v at constant pressure taking the system from (1) to (3) (with a concomitant increase in T) followed by a reduction in pressure at constant volume taking the system from (3) to 4) (with a concomitant decrease in T). Another path could involve moving along an isotherm from (1) to (2) (with a decreasing P and an increasing v) followed by an increase in pressure at a constant v taking the system from (2) to (4) (with an increasing T). A third path is the circuitous but direct path from (1) to (4). The point is that starting at (1), once at (4) the system has no memory of how it got there; the state is completely defined by the T, P, and v at (4). In turn, moving from (4) to a new state, e.g., (5) is unaffected by the path to (4).
3. Variables Defining the State of a Deformed Metal
In this section, the state variables characterizing a deformed metal are considered. Clearly, as in an ideal gas, temperature is one of these variables. One could argue that the pressure also should be included. However, most deformation processes occur at atmospheric pressure; accordingly, the pressure is only included as a state parameter when extremely high pressures are encountered, e.g., in metals subjected to high velocity plate impact or shock loading. Consider the mechanical test illustrated in Figure 2. In this test, a solid cylinder with a known, initial cross-sectional area (A0, m2) and a known, initial length (L0, m) on an (assumed) frictionless surface (fabricated from a very hard metal or ceramic) is subjected to an axial force (P, N). This is a compression test in which the application of the force P induces a permanent reduction of length (DL, m). To eliminate the crosssectional area as a variable, the force P is divided by the cross-sectional area A0 to give a stress, σ (N/m2 or Pa) according to
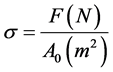 (3)
(3)
The stress σ is a likely candidate for a state variable. The change of length DL is divided by the initial length to give the strain ε accompanying the process according to:
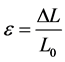 (4)
(4)
Because both DL and L0 have the same dimension, the strain is dimensionless. A final variable encountered in
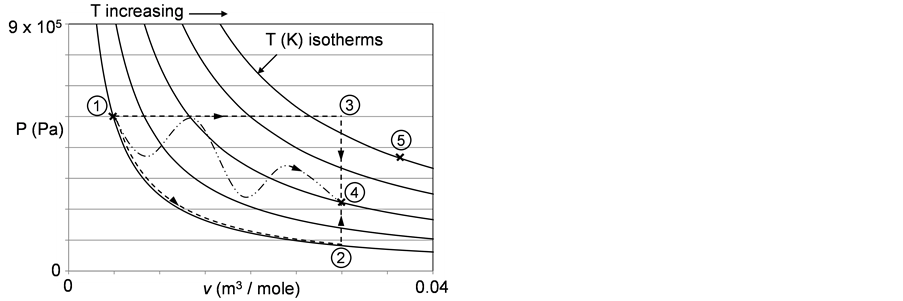
Figure 1. Variation of the pressure with the specific volume and temperature for an ideal gas. The concept of path independence is demonstrated by consideration of three distinct routes from state (1) to state (4).
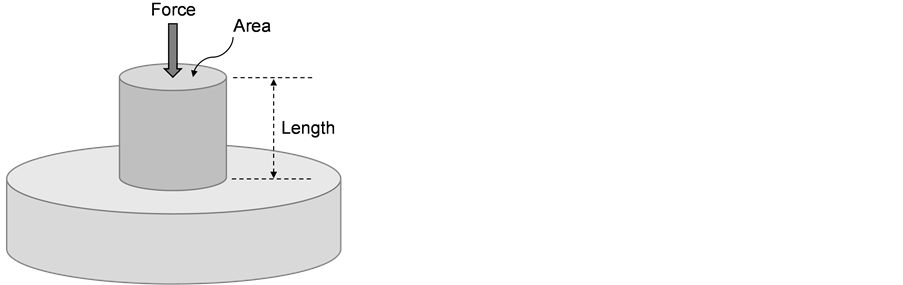
Figure 2. Configuration for a compression test of a solid cylinder with the cross-sectional area and length of the specimen identified.
mechanical tests is the rate at which the strain is imposed. This is described using the strain rate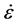 , defined as:
, defined as:
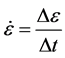 (5)
(5)
where Dε is the change in strain (dimensionless) over the time period Dt (s), which gives strain rate the dimension of s−1. While metals tend to be strain-rate insensitive in that their strength is usually weakly dependent upon strain rate, the opportunity for very large variations in strain rate makes this an important consideration. That is, the strain rate in a mechanical test using common test machines is on the order of 10−4 to 10−2 s−1. This implies that a strain of 0.20 is reached during the time period of 20 s to 2000 s, which is a convenient time period to run the test and acquire the measurements. But, the strain rates encountered during a bullet impact of armor or locally during a machining operation can easily reach 104 s−1. At this strain rate, a strain of 0.20 is reached within 20 μs!
Common constitutive laws for metal deformation relate the applied stress to temperature, strain, and strain rate:
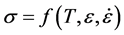 (6)
(6)
One example of this is a model proposed by Johnson and Cook [3] , written
 (7)
(7)
In this formulation, A, B, C, n, m, and Tr are constants and Tm is the melting temperature. For a specified temperature and strain rate—or for that matter for any temperature, strain-rate path—Equation (7) will predict how the stress varies with strain. The outstanding question is whether Equation (6), as well as the specific formulation given by Equation (7), represents a valid state variable model for metal deformation. This is considered experimentally in the following section.
4. Testing for Path Independence
An experiment was designed in 1987 to test the validity of Equation (6) as an internal state variable model [4] . The experiment involved compressing at room temperature two identical annealed copper specimens to the same strain. Sample A was compressed at a strain rate of 0.0001 s−1 to a final (unloaded) strain of 0.15. Sample B was compressed to the same strain at a strain rate of 9400 s−1. The latter experiment was performed in a split Hopkinson pressure bar (SHPB) with the specimen placed inside a donut that limited the total strain to 0.15. Figure 3 is a plot of the measured stress versus strain behavior on axes consistent with Equation (6). State (1) is the starting condition—annealed copper. During straining, the higher strain rate induces higher stresses in the sample2. The final state (2) consists of two samples at zero stress (the force in both specimens is brought to zero), room temperature, and a strain of 0.15. That is, the samples are indistinguishable in size and they are at a uniform stress (zero) and temperature. If Equation (6) were an applicable state-variable model, the two samples would be at an identical state. As in the perfect gas, the samples should be identical and should have no memory of how they were brought from (1) to (2). They should also exhibit identical stress versus strain curves when deformed from (2) at a specified temperature and strain rate to a new strain. This is precisely what was done next as part of this experiment.
To continue the experiment, both specimens were reloaded at room temperature and a strain rate of 0.001 s−1. As described above, these two specimens should behave identically if indeed they are in the same state. Figure 4 shows the resulting stress strain curves. The strain starts at 0.15, which is the final strain shown in Figure 3. Curiously, though, the stresses measured in Sample B are considerably higher than those measured in Sample A. This demonstrates that Samples A and B are definitely not identical; accordingly, they are not in the same state. There is some aspect of the higher strain rate path when compared to the slower strain rate path in Figure 3 that, even when strained to the same strain, has led to a higher strength material. This path dependence suggests that Equation (6) is not an internal state variable model, or that one or more of the variables listed in Equation (6) is not a valid internal state variable.
5. Why Is This Important?
While the inadequacy of strain as a state variable is evident, one might ask why this is important. The answer to this is partially in the path-dependence that accompanies Equation (6). However, if a modeler’s interest is a deformation process which is well described by a single temperature and strain rate, equations such as the constitutive formulation specified by Equation (7) can be fully adequate. With appropriate choice of model parameters, Equation (7) can be configured to predict the two stress-strain curves shown in Figure 3. The problem arises when changes in temperature or strain rate are imposed. Upon a change of strain rate, e.g., to 0.001 s−1 as in the sample B described above, Equation (7) is incapable of describing the trends shown in Figure 4.
In order to capture changes in temperature or strain rate, a constitutive model must accurately represent the operative kinetics of the deformation processes. With relation to chemical reactions, the term “kinetics” is used to describe the rates of reactions and dependencies on the chemical constituents. In deformation processes, kinetics refers to the dependencies of dislocation—obstacle interactions on temperature and strain rate [5] . A constitutive model must not simply reproduce a stress-strain curve, it must be able to accurately describe changes, e.g. the following derivatives,
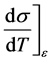 (8)
(8)

Figure 3. Variation of stress with strain for two identical copper test specimens deformed at room temperature and two strain rates.

Figure 4. Stress-strain curves—reload stress-strain curves— measured at room temperature and a strain rate of 0.001 s−1 on the two specimens described in Figure 3.
and
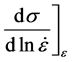 (9)
(9)
One example of where these derivatives become influential is in the formation of a neck in a tensile test. The French researcher Considère showed that the point of instability in a tensile test, i.e., the point at which the neck forms, is when3
 (10)
(10)
For the case of a material that exhibits power-law hardening defined by
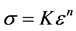 (11)
(11)
where n is the hardening exponent (usually, n < 0.5), it is easily shown that the instability strain εn equals the hardening exponent. For a material that follows a temperature and strain-rate dependent constitutive law, such as described by Equation (6), Equation (10) still applies but the total differential includes temperature and strain rate terms which will influence the instability strain.
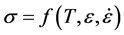 (6)
(6)
 (12)
(12)
It is rare in deformation scenarios that only the stress-strain curve under some prescribed (and constant) temperature and strain rate is of interest. Most deformation processes involve regimes of varying strain rate and/or temperature. The need to predict instabilities, such as the formation of a neck in a tensile test or shear band in a structure, is also quite common. This is why the model must be able to accurately describe the applicable deformation kinetics and why the state variables need to reflect the true state of the system.
6. Toward an Internal State Variable Constitutive Model
The results presented in Figure 4 strongly suggest that strain (ε) is not a valid internal state variable, because samples deformed to the same strain at different strain rates are not identical. As an alternative to strain, Mecking and Kocks [6] suggested use of the mechanical threshold stress 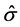 as an internal state variable4. The mechanical threshold stress is the yield stress at 0 K. It is an intrinsic measure of the stress at the onset of yielding without the assistance of thermal activation. The value of the threshold stress can be estimated by measuring the yield stress as a function of temperature and extrapolating to 0 K. Procedures to do this along with several examples are detailed in [1] . (See in particular, Sections 4.5, 4.6, 6.3, and 7.2 and the many examples in Chapters 8 - 10.)
as an internal state variable4. The mechanical threshold stress is the yield stress at 0 K. It is an intrinsic measure of the stress at the onset of yielding without the assistance of thermal activation. The value of the threshold stress can be estimated by measuring the yield stress as a function of temperature and extrapolating to 0 K. Procedures to do this along with several examples are detailed in [1] . (See in particular, Sections 4.5, 4.6, 6.3, and 7.2 and the many examples in Chapters 8 - 10.)
Although estimating the mechanical threshold stress can be tedious, an extensive set of experiments performed by Follansbee and Kocks demonstrated these measurements in copper over a range of strains and strain rates [7] . These measurements support the notion that strain is not a valid state variable. Figure 5 shows measurements (open diamonds) of the stress at a constant strain of 0.20 in copper as a function of strain rate. The “hockey stick” trend at strain rates exceeding ~1000 s−1 had been observed by many investigators [8] [9] in several materials and had been of great interest to the deformation community because of the implications for deformations at even higher strain rates. Follansbee and Kocks also estimated the mechanical threshold stress—the yield stress at 0 K—in samples deformed to a strain of 0.20 at seven strain rates (from 10−4 s−1 to 9500 s−1). The measurements included in Figure 5 as open boxes with an error bar demonstrate that the mechanical threshold stress increases with increasing strain rate in a manner that is similar to the variation of the stress at the strain of 0.20. Even the “hockey stick” trend is reflected at the higher strain rates. These measurements validated the notion that samples deformed to the same strain along different strain-rate paths are not identical.

Figure 5. Stress at a strain of 0.20 measured at room temperature on identical copper specimens from strain rates of 0.0001 s−1 to ~10,000 s−1. Included are measurements of the threshold stress for samples deformed at seven of the strain rates to the strain level of 0.20.
The mechanical threshold stress is one suggested internal state variable applicable to the deformation of copper. Sections 6.5 and 8.1 of [1] relate this variable to the stored dislocation density. Other threshold stress variables are introduced to model the contributions of additional strengthening mechanisms found in metallic alloys. The premise in [1] (see Section 6.3) is that the internal state variable model is of the form
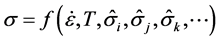 (13)
(13)
where 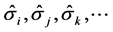 represent specific mechanical threshold stress variables associated with solute concentrations, defect densities, crystallographic orientations, etc. (For examples of these approaches, the reader is referred to Barbe, Decker, Jeulin, and Cailletaud [10] , Arsenlis and Parks [11] , and Horstemeyer, Baskes, Prantil, Philliber, and Vonderheide [12] ). The constitutive modeling community continues to work to define appropriate internal state variables to support the search for an ideal-gas like model for deformation.
represent specific mechanical threshold stress variables associated with solute concentrations, defect densities, crystallographic orientations, etc. (For examples of these approaches, the reader is referred to Barbe, Decker, Jeulin, and Cailletaud [10] , Arsenlis and Parks [11] , and Horstemeyer, Baskes, Prantil, Philliber, and Vonderheide [12] ). The constitutive modeling community continues to work to define appropriate internal state variables to support the search for an ideal-gas like model for deformation.
Acknowledgements
The author appreciates the support of Saint Vincent College in the writing of [1] and the compilation of this manuscript.
NOTES
1Recall that a mole is a quantity of a substance with as many particles (e.g., atoms) as found in 12 grams of the most abundant isotope of carbon (12C). This amounts to 6.022 × 1023 particles, which is referred to as Avogadro’s number.

2At the higher strain rate, the sample temperature will increase slightly because at these short time spans there is insufficient time for the heat generated by the work characterized by (F dL to flow to the surroundings. In annealed copper, this temperature rise is relatively small (~7 K) and it works to decrease the stress, which is in a direction opposite to the trends described in the following paragraph.

3This is easily derived starting with σ = F A, setting the differential dσ = 0, and invoking the constant volume condition.

4The term “yield” here refers to the temperature and strain-rate dependent stress at the onset of plastic flow in a sample in some specified state, which may or may not be the annealed state. The use of the term “prestrain” for the deformation conditions that produce a state in the material, and the use of the term “reload” for the experiment that measures the yield stress of samples in this state provides some clarification.