1. Introduction
In this article we make a modest attempt to provide an expository account of fractal interpolation from the point of view of a numerical analyst and an approximation theorist. No claim of completeness is made and there is likely a bias towards the interests of the authors in the selection of materials.
The basic focus of interpolation is the reconstruction of an unknown function in a continuum from its availability in some grid points and thereby links the discrete world with the continuous one. There are multitudes of interpolation methods using various families of functions; polynomial, exponential, rational, trigonometric and splines to name a few.
Despite of a large number of interpolation schemes available in the classical numerical analysis, it should be noted that all these conventional nonrecursive interpolation methods produce interpolants that are differentiable a number of times except possibly at a finite set of points. However, many real world and experimental signals are complex and rarely show a sensation of smoothness in their traces. Consequently, to model these signals, we require interpolants that are nondifferentiable in dense set of points in the domain. To address this issue, Barnsley [1] introduced Fractal Interpolation Function (FIF) using the theory of Iterated Function System (IFS) [2] .
Barnsley and Harrington [3] observed that if the problem is of differentiable type, the parameters of the IFS can be so chosen that the resulting FIF is 
-continuous. This observation leads to fractal splines—a hybrid born from the cooperation of fractal functions and splines. The fractal splines can include traditional splines as special cases—a fact that should be of interest to a numerical analyst. Further, in contrast to a traditional spline, a fractal spline 
possesses the derivative 
with varying irregularity that can be quantified in terms of fractal dimension, and one can use the fractal dimension of the graph of 
as an index for the analysis of the underlying experimental process.
Using the notion of FIF, Navascués constructed an entire family of fractal functions 
parameterized by a suitable vector 
in Euclidean space associated with a prescribed continuous function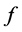 
on a compact interval
. Further, the operator 
that stems from this “fractal perturbation” was introduced and extensively studied by Navascués [4] -[6] . This tool facilitates the FIF theory to interact with fields such as functional analysis, approximation theory and operator theory.
2. Fractal Interpolation Theory: An Overview
A FIF can be slickly defined as an interpolant whose graph is a fractal in the following sense.
Definition 2.1 An IFS 
consists of a complete metric space 
with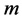 
continuous maps
. The IFS 
is called hyperbolic if each 
in 
is a contraction, i.e., if there exists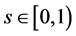 
such that 
for all
.
Given an IFS
, the set of nonempty compact subsets of 
is denoted by
. It is well-known that 
endowed with the Hausdorff metric is complete. Define the Hutchinson operator 
by
. For
, let 
denotes the 
-fold autocomposition of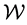
.
Definition 2.2 A set 
is called an attractor of 
(or a deterministic fractal associated with
) if 
for any arbitrary
, where the convergence is with respect to the Hausdorff metric. Also 
is said to be an invariant set if
.
A basic result in the theory of IFS is the following:
Theorem 2.3 (Barnsley [1] ). A hyperbolic IFS possesses a unique attractor, which is invariant under the Hutchinson operator.
Note that the contractivity of 
is not integral to the existence of an attractor. For instance, if 
is compact and each 
is continuous, then 
has an attractor, albeit unicity cannot be ensured [1] .
Next we describe how to obtain interpolants whose graphs are fractals in the sense of Definition 2.2. Let 
be a natural number. Let 
be real numbers, and
. Consider a set of data points
. Set
. For
, set
, and let 
be homeomorphisms such that
(1)
(2)
Let
. Consider 
continuous maps 
satisfying
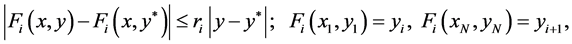(3)
where
, 
, and
. Now define 
For the IFS
, Barnsley presented the following seminal result.
Theorem 2.4 (Barnsley [1] ) The following hold:
1. The IFS 
has a unique attractor 
such that 
is the graph of a continuous function 
satisfying 
for
.
2. Let 
be endowed with the uniform metric
. If,
, then
has a unique fixed point
, and 
for any
. Further, the fixed point 
is the function satisfying condition given in (i).
Definition 2.5 The function 
which made its debut in the previous theorem and whose graph is the attractor of an IFS is called a Fractal Interpolation Function, FIF for short.
Most extensively studied fractal functions in the theory and applications heretofore are defined by the IFS 
with constituent maps
(4)
where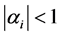
. The coefficients of the affine maps 
are determined through the conditions prescribed in (2), and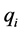 
are suitable continuous functions so that the maps 
satisfy conditions in (3). A possible explanation for the choice of this special class of IFS is that the corresponding FIF is explicitly integrable and a satisfactory theory for moment integrals can be developed. If in (4), 
are taken as affine maps for all
, then the IFS is a particular case, namely an affine IFS. and the corresponding FIF is termed as an affine FIF, which has received much attention. For instance, using affine FIFs, a procedure for the numerical quadrature of functions displaying some kind of fractal complexity is proposed in [7] .
The affine case has been extensively studied by the authors. In reference [8] , the operator of affine fractal interpolation is defined and developed. Its linearity and continuity is proved. In the same paper, the authors obtain some bounds of the approximation error, in terms of the scale factors and by means of the Lebesgue constant of the partition chosen. Sufficient conditions for the convergence of the procedure are also provided. Another interesting contribution is the finding of Schauder bases of the space
, consisting of affine fractal functions. Their existence is proved in the references [9] [10] , using scale vectors whose magnitude is bounded in different ways.
The polynomial IFS, that is the IFS obtained by taking
, 
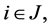to be suitable polynomials in (4) are also investigated (see, for instance, [11] [12] ). Following Theorem 2.4, the FIF 
corresponding to the IFS 
satisfies the functional equation
(5)
Often the graph of 
(cf. (5)) has noninteger Hausdorff-Besicovitch and Minkowski dimensions; 
may then be Hölder continuous but not differentiable. To put in a nutshell, the main differences of a FIF 
(to emphasize the dependence of 
on
) from the traditional interpolation techniques lie in 1) the construction via IFS theory that offers a self-similarity in small scales 2) the construction by iteration of the interpolant instead of using an analytic formula 3) the usage of scaling factors (which are strongly related to the fractal dimension of the graph of the interpolant) which offers flexibility in the choice of an interpolant in contrast to the unicity of a specific type of traditional interpolant.
For a given data set, with the help of so-called scaling factors
, 
, the interpolating curves may be modified at the discretion of the user, which indeed is a good news as far as geometric design environment is concerned. Though splines with parameters are available in the traditional numerical analysis as well, these parameters cannot influence the smoothness of the constructed interpolant. The closeness of fit of a FIF with the original function is mainly influenced by the determination of so-called vertical scaling factors. There does not exist a unified approach that can efficiently answer the question on “optimal” choice of these scaling factors. Given a
, task of finding an 
for which the fractal interpolant 
is close to 
is a constrained convex optimization problem [9] . Upper and lower bounds of the vertical scaling factors that constrain an affine fractal interpolation function within an axis-aligned rectangle are determined in [13] . Recently, this type of containment problem is solved with a general method that does not rely on the affinity of the IFS and successively employed by taking cubic FIF as an example [14] .
Since a FIF is defined recursively using an implicit functional equation, a possible objection to the fractal method may be that in principle, to obtain an actual interpolant, one needs to continue the iterations indefinitely. However, in practice, a small number of iterations gives a sufficiently good approximation. From the given 
data points and by using the injective maps 
we obtain values of the FIF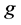 
exactly at 
distinct points at the 
-th iteration (see [5] ), thus the computation is very fast and a good view of the whole function is quickly obtained. Though a FIF 
is commonly expressed by a recursive functional equation as in (5), an explicit representation (in terms of an infinite series) of 
on 
can be given (see [15] ). Computing numerical approximations to attractors and evaluation of FIFs at specified points are based on addresses and code spaces [16] , and stable methods such as the chaos game algorithm can be used for computing FIFs. Therefore, there is no reason to resist the use of FIF with regard to the evaluation of the interpolant at a point.
As a class of continuous functions, the smoothness of FIFs is a valuable problem which has been studied by several researchers (see, for instance, [17] ). To get FIFs with more flexibility and diversity, FIFs with variable scaling parameters are constructed and analytical properties such as smoothness, stability, sensitivity analysis are investigated in [18] .
The following result was instrumental in the marriage of fractals and splines.
Theorem 2.6 (Barnsley and Harrington [3] ). Let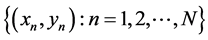 
be the prescribed set of interpolation data, where
. Let
, satisfy (2) and
satisfy (3). Suppose that for some integer
, 
and
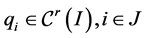. Let
If 
for 
and
, then the IFS 
determines a FIF
, and 
is the FIF determined by 
for
.
Based on this theorem several researchers have constructed fractal analogues of various traditional nonrecursive splines (see, for example, [3] [11] [12] [14] ) which indeed emerge as special cases of fractal splines when 
for all
. Thus the theory of FIF provides a wide spectra of interpolation schemes ranging from nowhere differentiable interpolants to infinitely differentiable interpolants such as polynomials. Adjective fractal in FIF should not be confused with irregularity, however, the name fractal interpolation function is used because of the flavor of the scaling in the definition and because some derivative of these functions is typically fractal. Since the graph of FIF is a union of transformed copies of itself, an alternative name could be self-referential function.
Apart from smoothness there are several other desirable properties such as approximation order, locality and shape preservation for an interpolant. In what follows, we attempt to compare the traditional and fractal interpolation with respect to these properties. It has been demonstrated that with suitable mild condition on the scaling factors, a smooth FIF has the same order of convergence as that of its classical counterpart which is to be considered along with the flexibility offered by the fractal method (see, for instance, [11] [12] ). It is not hard to see that the value of a FIF at a point 
in the interpolation interval depends not only on the data points 
for which 
is near to 
but on the entire data points, thus a fractal interpolation scheme is not local. In this regard the following points are worth to mention. We may have to sacrifice a certain requirement to achieve certain other. Even for interpolation with traditional cubic interpolant, to gain total localness we must sacrifice global continuity in the second derivative and vice versa. Similarly, for pronounced irregularity in the interpolant or a suitable derivative, we have to choose large values of 
(see [1] ), whereas a total locality may be gained by taking 
for all
. Putting it in different words, we are not replacing a completely local traditional interpolation scheme with a new one but with a more flexible and versatile scheme which recovers it.
The subfield of interpolation wherein one deals with the construction and implementation of interpolation schemes that constrain the range of an interpolant or its suitable derivative so as to yield a credible visualization of a prescribed data set by adhering to the geometric properties (for example, positivity, monotonicity, convexity) inherent in data is generally referred to as shape preserving interpolation or isogeometric interpolation. There is a plethora of traditional shape preserving interpolation schemes in the literature. However, these shape preserving schemes are unsatisfactory to handle situations wherein a prescribed data set possesses certain shape characteristics, and at the same time, data representing a certain derivative should be modelled with a function having irregularity in a dense subset of the interpolation interval. This issue motivated us to unify the two methodologies—fractal interpolation and shape preserving interpolation—that seem to be developing independently and in parallel (see, for instance, [14] [19] ). It should also be noted that for an effective exposition of FIFs to shape preserving interpolation we shall obviate the common assumption of polynomiality of the maps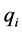 
in (5) and allow them to be rational functions.
As mentioned earlier, FIFs are self-referential. To model a function or a data set with non-self-referential nature Barnsley et al. [20] initiated the notion of hidden variable FIFs. For simulating curves that exhibit partly self-referential and partly non-self-referential nature, coalescence hidden variable FIF is introduced in [21] . Considering construction of a smooth interpolant with fractality (irregularity) in certain derivative, a closest competitor for fractal schemes may be subdivision schemes. For a comparison of these two traditions, the reader is referred to [14] . Though our main intent is to consider univariate fractal interpolation function, let us close this section by remarking that some progress towards the construction of fractal interpolation surfaces can be found in [22] -[25] .
3. Fractal Functions in Approximation
In this section we demonstrate that any continuous function defined on a compact interval can be regarded as a special case of a class of continuous fractal functions. This was first observed by Barnsley [1] and developed by Navascués (see, for instance, [4] -[6] ).
Let
. Here, we consider the special case of (4) wherein
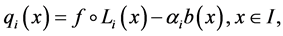(6)
is a continuous function satisfying
, 
, and
; 
.
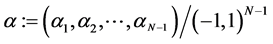Definition 3.1 The continuous function 
whose graph is the attractor of the IFS defined through the maps (4) and (6) is referred to as an 
-fractal function associated with 
with respect to 
and the partition
. The function 
is referred to as a base function.
In view of (5), 
satisfies the functional equation
(7)
Notice that if
, then
. Consequently, (7) associates a family of continuous functions with each fixed function
. The degrees of freedom offered by this procedure may be useful when some problems combined with approximation and optimization have to be approached.
Assume that the continuous function 
occurring in (6) depends linearly on
, say for instance, 
, where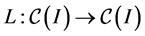 
is a linear and bounded operator with respect to the uniform norm or 
-norm on
. Then the map
, defines a linear operator referred to as an 
-fractal operator. Basic properties of this operator including the following among others are established in the references [4] -[6] .
Theorem 3.2 Let 
be such that 
and 
be the identity map on
.
1. The operator 
is a bounded linear map and
.
2. If
, then 
is injective.
3. For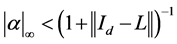
, the operator 
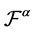is a topological isomorphism.
Remark: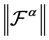 
represents the norm of the operator with respect to the uniform (or supremum) norm in the space
.
Estimates for the approximation of a continuous function by its fractal analogues can be obtained from the following Proposition.
Proposition 3.3 (Navascués [26] ) Let 
and let 
be such that
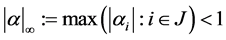. Then
.
From the fact that 
for 
and the above Proposition, it can be readily seen that for suitable choices of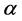
, the fractal function 
simultaneously interpolates and approximates
. In general, constructing a differentiable FIF by finding an IFS satisfying hypotheses of Theorem 2.6 is difficult, mainly when some specific boundary conditions are required. The following theorem describes a very general way of constructing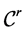 
-continuous 
-fractal function 
whenever the germ function
.
Theorem 3.4 (Navascués et al. [27] [28] ) Let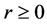 
and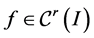
. If the scaling factors satisfy 
for all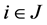
, the base function 
in (6) is selected such that 
is
—continuous, 
and 
for
, then the fractal function 
is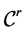 
-continuous.
Usually, a class of approximants are determined by considerations peculiar to the applications one is interested in; by considering the 
-image of the most fundamental approximation class, namely the class of polynomials, Navascués [4] has introduced the class of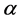 
-fractal polynomials and investigated its approximation and topological properties. In [5] , a family of fractal functions is assigned to several classes of real mappings like, for instance, maps defined on sets that are not intervals, maps integrable but not continuous and may be defined on unbounded domains. Recently, the authors have identified suitable elements of the IFS so that the fractal function 
preserves the fundamental shape properties of 
and deduced fractal analogues of some elementary theorems in shape preserving approximation [28] . This opens the door to shape preserving fractal approximation.
The operator 
of Theorem 3.2 can be extended to the Lebesgue spaces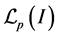
. In the reference [29] , the author defines fractal functions forming a Schauder basis for the space of 
-integrable functions, using the extended version of
.
4. Applications
The reader can undoubtedly discern with the fact that the fractal splines are friendly hybrid birds offering more versatility in the process of interpolation and approximation. Given the general scope of fractal interpolation and its interconnection with numerical analysis and approximation theory, it is not difficult to find applications of FIFs in fields such as geometric design, data visualization, physics and chemistry, image compression, and signal processing. Further, as classical splines are special cases of fractal splines, it should be possible to use fractal splines for mathematical and engineering problems where the classical spline interpolation does not work satisfactorily. In reference [26] , fractal interpolation of electroencephalographic recordings is used in order to describe the increase in the bioelectric complexity during some tests of attention in children and to compute other electroencephalographic parameters. Using theory of FIFs, low-cost procedures for the quantification and representation of EEG signals in the time and space domains are proposed in [30] .
As explained previously, an important application of fractal interpolation to the numerical analysis is the generalization of all the methods of interpolation and approximation, defining new families of fractal functions which contain the classical approximants (polynomial, spline, trigonometric) as a particular case.
Fractal interpolation can be used to compute the spectral content of an experimental signal as well. For instance, the Fourier powers can be computed by means of the moments defined in [1] . This procedure is developed in the reference [31] . The parameters obtained display the macroscopic cycles underlying the observed phenomenon.
Using mathematical tools similar to the previous one, we developed orthogonal expansions of a sampled signal, like for instance Legendre series ([32] ). These finite sums provide curves of approximation of the described phenomenon. In all cases, the goodness of the methods employed is analyzed. In general, we deduce an upper bound of the approximation error on the basis of the number of terms and the sampling step. These inequalities provide further sufficient conditions for the convergence of the procedure.
This concludes our very rapid survey of existing techniques and ideas in FIFs. Many works in this field are left out; however, we believe that the current exposition will provide an overall flavor of the subject to a numerical analyst/applied mathematician who is a novice to fractal interpolation and perhaps serves also as a titbit for an informed reader. Our earnest aspiration is that FIFs turn out to be a good servant for all those working with interpolation theory, and the topic of fractal interpolation and approximation can be found in all standard books on numerical analysis and approximation theory.