1. Introduction
The part of mathematics that deals with the properties of specific types of numbers and their uses in puzzles and recreational mathematics has always fascinated scientists and mathematicians (O’Beirne 1961 [1] , Gardner 1987 [2] ).
In this short paper, we will talk about digital roots—a well-established and useful part of recreational mathematics which materializes in as diverse applications as computer programming (Trott 2004) [3] and numerology (Ghannam 2012 [4] ). As will see, digital roots are equivalent to modulo 9 arithmetic (Property 1.6) and hence can be thought of as a special case of modular arithmetic of Gauss (Dudley, 1978) [5] .
Let us start out by the following existence theorem:
Theorem 1.1. Let 
be a natural number and let 
denote the sum of the digits of
. In a finite number of steps, the sequence 
becomes a constant.
Proof. Let
, where for any
,
. This implies that
If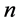 
is a one digit number, that is if
, then, 
is the required constant. Else, at least one of 
is positive and,
Thus, repeatedly applying the s operator, we will get a decreasing sequence of numbers. Once a term of this sequence becomes a single digit number, from then on the sequence will remain a constant.
Definition 1.1. Let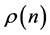 
denote the constant value the sequence 
converges to. We call 
the digital root of
.
Here are some simple properties that follow immediately from this definition:
Property 1.1.
, where 
stands for the geatest integer less than or equal to
.
Property 1.2. 
Property 1.3.
.
Property 1.4.
.
Property 1.5.
.
Property 1.6.
This 
symmetric matrix Table 1, which is formed by replacing the numbers in a regular 
multiplication table by their digital roots, is referred to as a Vedic square. Vedic squares have been used extensively to create geometric patterns and symmetries, and even musical compositions by highlighting specific numbers. For more information see Pritchard (2003) [6] .
Closely related to the concept of digital roots is that of additive persistence, which is defined as the number of (additive) steps required to obtain its digital root. We will denote the additive persistence of a nonnegative integer n by
. Clearly, for any single digit number n the additive persistence is 1.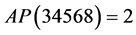
, because we need two steps to obtain
:
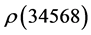Step 1. 
Step 2. 
The smallest number with additive persistence of 
is
1 followed by
’s. For more information on additive persistence see Hinden (1974) [7] .
Some Well-Known Results
Proposition 1.1. Digital root of a square is 1, 4, 7, or 9.
By Property 1.2, the digital root of 
is
which can only be 
.
Proposition 1.2. Digital root of a perfect cube is 1, 8 or 9.
Proof is similar to the one given above.
Proposition 1.3. Digital roots of the powers of a natural number x form a cyclical sequence. This cycle is the same for all numbers
, where k is any natural number:
This follows because for any
, 
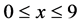and for any two natural numbers 
and 
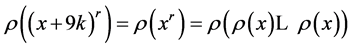
We can use Table 2 to compute digital roots of powers of large numbers. For example,
Proposition 1.5. Digital root of an even perfect number (except 6) is 1.
Proof. Every even perfect number 
is of the form
Table 1 . The multiplication table for digital roots is the familiar modulo 9 multiplication table with 0 replaced by 9.
Table 2. Digital roots of the powers of a natural number x form a cyclical sequence.
where 
is a Mersenne prime. By putting
, we have
Here, the last equality follows from properties 1, 2, and 3 above.
By proposition 1.2,
and
Hence the result follows.
To generalize the concept of digital roots to any other base
, one should simply change the 9 in the formulas to
. For more information on digital roots see Averbach and Chein (2000) [8] .
In the following sections, we will prove some results on digital roots of powers of numbers in an arithmetic progression as well as digital roots of Fermat numbers and star numbers.
2. Digital Roots of Powers of Numbers in an Arithmetic Progression
We start with the following Proposition 2.1. Let k, m and n be three consecutive terms in an arithmetic progression with common difference
. Let
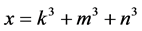
If d is not a multiple of 3, then
.
Proof. Let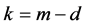 
and
. Then
Consequently, to prove the proposition, we must prove 
is divisible 3 by for any natural number m and for any natural number d that is not a multiple of three.
If m is divisible by 3, the result follows. So, let us consider the two cases:
Case 1.
. In this case
Since
,
Thus,
Case 2.
. In this case
Again,
Thus,
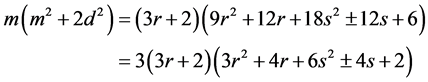
Remark. The restriction on 
is necessary. For example, let 
and
.
Then,
and
Using the fact that a sum is divisible by a positive integer if all terms are divisible by a positive integer we get Theorem 2.1. Let q be a multiple of three. Let 
be any q consecutive terms of an arithmetic progression whose common difference d is not a multiple of three. Let
Then,
.
For example, let
, 
, 
, 
, 
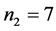and 
Then,
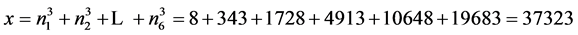
and
.
Again if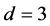
, this does not hold. As a counterexample,
, 
, 
, 
, 
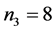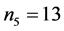and 
and
.
Corollary 2.1. Let q be a multiple of three. Putting
, we get that the sum of the cubes of q consecutive integers is divisible by 9. Putting
, we get that the sum of the cubes of q consecutive odd integers (even integers) is divisible by 9.
Although similar results do not necessarily hold for sixth powers, we show that they do for ninth powers. In fact, we find out that the restriction on d is not needed for ninth powers.
Proposition 2.2. Let 
be nine consecutive terms in an arithmetic progression with common difference d. Let
Then,
.
Proof. This follows by writing
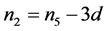
and noting that
Using the fact that a sum is divisible by a positive integer if all terms are divisible by a positive integer we get Theorem 2.2. Let 
be a multiple of nine. Let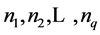 
be any 
consecutive terms of an arithmetic progression whose common difference d. Let
Then,
.
Corollary 2.2. Let 
be a multiple of nine. Putting
, we get that the sum of the ninth powers of 
consecutive integers is divisible by 9. Putting
, we get that the sum of the ninth powers of 
consecutive odd integers (even integers) is divisible by 9.
3. Digital Roots of Fermat Numbers
As is well-known, a Fermat number 
is defined as
For computational purposes the following recursion formula is useful:
Theorem 3.1. For
,
Proof. Since
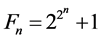
and for
,
Thus,
Thus,
and the formula follows.
Inspection of the first few Fermat numbers F0 = 3, F1 = 5, F2 = 17, F3 = 257, F4 = 655373, F5 = 4294967297…shows that for
, 
is 5 if 
is odd and 8 if 
is even. In fact, this is indeed true for all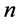
:
Theorem 3.1. Let 
be the 
Fermat number. Then,
Proof. Proof is by induction. Clearly, the claim is true for
. Assume it is true for
. Then,
Suppose 
is odd. Then
Suppose 
is even. Then
4. Digital Roots of Star Numbers
The 
star number (so called because geometrically these numbers can be arranged to represent hexagrams) is denoted as 
and is of the form
for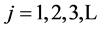 
So, 
, 
and so on. It is easy to show that
for 
Pictorially, 
can be represented as
•
and 
as
•
••••
•••
••••
•
depicting the six-cornered star shape.
Clearly, 
In factLemma 4.1. The digital root of a star number is always 1 or 4. In fact, the progression of digital roots of star numbers is 
Proof. Since the digital root of any integer is one of
, the digital root of a product of the form 
is 
(0 represented as 9). Consequently, the digital root of a product of the form 
is one of
. Hence the digital roots of star numbers are 
5. An Application
Here is a problem simple problem.
Prove that
is divisible by 9.
Here we will apply Proposition 2.1. We write
But by Proposition 2.1 the sum in each parenthesis is divisible by 9, and hence so is their sum, and their sum plus 9.
Here is another problem that can be solved using digital roots. Problems similar to this one can be found in Polya (1957) [9] and (Noller, et al. 1978) [10] .
Suppose we have a five-digit number. We are given that this number is divisible by 72. Starting with the first one, how many digits of this number must be disclosed before we can uniquely determine it?
Assume we are given the first digit, say 4. Obviously, more information will be needed before a unique solution is found. For example, 
, 
all fit the bill. So, assume now the second digit is also given, say 8. Again, we cannot find a unique solution based on this information:
, 
are all possible solutions. So, assume one more digit is given, say 9. We claim this would be enough to solve the problem.
If a number is divisible by 72, it must be divisible by both 8 and 9. But a number is divisible by 8 only if one of the two conditions holds: The hundreds digit is even and the last two digits are a multiple of 8 or the hundreds digit is odd and the last two digits are a multiple of 4 but not 8. Since in our example the hundreds digit is odd, the last two digits of the number we are looking for must be a multiple of 4 but not 8, that is, the last two digits must be one of 
On the other hand, to be divisible by 9, the digital root of the number must be 9.
Since
we know that the number must be
.