Existence and Uniqueness of Positive Solution for Third-Order Three-Point Boundary Value Problems ()
1. Introduction
In this paper, we consider the uniqueness and existence of the positive solution for the following third-order differential equation
(1)
or
(2)
with the following three-point boundary conditions
. (3)
Throughout this paper, we assume that 
may be singular at 
and/or 
and
. Here, the solution 
of the BVP (1)-(3) (or the BVP (2)-(3)) is called positive if
.
In the past few years, because of the extensive applications in mechanics and engineering, the existence of solutions or positive solutions for nonlinear singular or nonsingular three-point boundary value problems for third-order ordinary differential equations has been studied extensively in the literature (see [1] -[13] and references therein). For example, in the case of 
and 
is nonsingular at 
and
, Guo et al. [1] [2] established some existence results of at least one and at least three positive solutions for the BVP (1)- (3) by using the well-known Krasnosel’skii fixed point theorem and the Leggett-Williams fixed point theorem, respectively. By using the upper and lower solutions and the maximum principle, Yao and Feng in [14] and Feng and Liu in [15] studied the existence of solutions for the BVP (1)-(3) and BVP (2)-(3) with
, respectively.
Motivated mainly by the papers mentioned above, in this paper we will consider the uniqueness of the positive solution, the iteration and the rate of the convergence by the iteration for the nonlinear singular third-order three-point BVP (1)-(3). We study the existence of the positive solution for the nonlinear third-order three-point BVP (2)-(3) by using the Leray-Schauder fixed point theorem.
The rest of this paper is organized as follows. After this section, we present some notations and lemmas that will be used to prove our main results in Section 2. We discuss the uniqueness in Section 3. Finally, we discuss the existence in Section 4.
2. Preliminaries
In this section, we introduce definitions and preliminary facts which are used throughout this paper.
Definition 1 Let 
be a real Banach space. A nonempty closed convex set 
is called a cone of 
if it satisfies the following two conditions:
1) 
implies
;
2) 
implies
.
Definition 2 An operator is called completely continuous if it is continuous and maps bounded sets into precompact sets.
The following lemma plays a pivotal role in the forthcoming analysis.
Lemma 3 [9] Suppose that
, 
, then the unique solution of the following equation
(4)
with boundary conditions (3) is given by
(5)
where
(6)
(7)
and
We need some properties of functions 
and 
in order to establish the existence and uniqueness of positive solutions.
Lemma 4 For all
, we have
Proof The conclusion is obvious. The proof is completed.
Lemma 5 For all
, we have
(8)
Proof For all
, if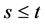
, it follows from (7) that
and
If
, then from (7) we have
The proof is completed.
Lemma 6 The Green’s function 
has the following properties:
(9)
(10)
Proof After direct computations, we easily get
(11)
(12)
From (11) and (12) we can get (9) and (10) respectively. The proof is completed.
3. Uniqueness
We shall consider the Banach space 
equipped with norm
.
Theorem 7 Suppose that
(H1) 
for any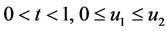
;
(H2) There exist 
such that
(H3) 
Then the BVP (1)-(3) has an unique positive, nondecreasing solution
, here
. (13)
Constructing successively the sequence of functions
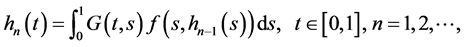(14)
for any initial function
, then 
must converge to 
uniformly on [0, 1] and the rate of convergence is
(15)
where
, which depends on the initial function
.
Proof Obviously, from (H1) we obtain
(16)
Let
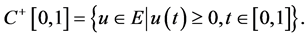
In view of Lemma 3, we define an operator T as
. (17)
By (H1) it is easy to see that the operator 
is increasing. Observe that the BVP (1)-(3) has a solution if and only if the operator T has a fixed point.
In what follows, we first prove 
In fact, for any 
there exist positive numbers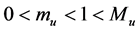 
such that
It follows from (H2) and (16) that
(18)
Using (17), (18), (8) and the condition (H1), we obtain
(19)
and
(20)
Equations (19), (20) and (H5) imply that
.
For any
, we let
(21)
and
(22)
Since the operator 
is increasing, (H1), (H2), (21) and (22) imply that
(23)
For
, from (H1), (17) and (22), it can obtained by induction that
(24)
From (23) and (24) we know that
(25)
so that there exists a function 
such that
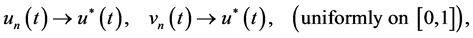(26)
and
(27)
From (H1) and (22) we have
This together with (26) and uniqueness of the limit imply that u* satisfy
, thus 
is a solution of the BVP (1)-(3).
Form (22), (23) and (H1), we obtain
(28)
It follows from (26), (27) and (28) that
Therefore,
So that (15) holds. Since 
is arbitrary in D we know that 
is the unique solution of the BVP (1)-(3) in D.
Remark If 
is continuous on
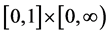, then it is quite evident that the condition (H3) holds. Hence the unique solution 
is in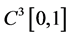
.
4. Existence
Now we are ready to discuss the existence of positive solutions for the BVP (2)-(3).
Theorem 8 Suppose that
(H4) 
and 
(H5) There exists positive number 
such that
(29)
where M is defined by (11).
Then the BVP (2)-(3) has at least one positive solution 
such that
(30)
Proof We consider the Banach space 
equipped with the norm
(31)
where
.
For
, define the operator S by
(32)
By Ascoli-Arzela Theorem, it is easy to known that the operator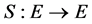 
is a completely continuous operator. The BVP (2)-(3) has a solution 
if and only if 
is a fixed point of operator S defined by (32).
Let
then 
is a bounded closed convex set of E. We show that
. For
, by (31) we have
which implies that
Therefore, by (9), (10), (29) and (32) we get
(33)
and
(34)
Then (33) and (34) show that
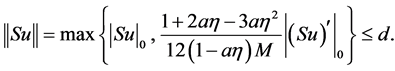
i.e.,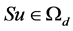
. Thus, by Leray-Schauder fixed point theorem, S has a fixed point
, which implies that BVP (2)-(3) has at least one positive solution 
satisfying (30). This completes the proof.
Acknowledgements
The authors thank the referee for her/his careful reading of the paper and useful suggestions. This work is supported by Hangzhou Polytechnic (KZYZ-2009-2) and the Natural Science Foundation of Zhejiang Province of China (LY12A01012).
NOTES
*Corresponding author.