Keywords
Negative Volume, Short Sales, Put Options, Mergers

1. Introduction
In their seminal paper on short selling at merger announcements, Mitchell, Pulvino and Stafford [1] set forth that acquirers who exchange stock with target firms release negative signals of depleted cash reserves. They observed significant negative cumulative abnormal returns on acquirer stock in stock mergers. On the day prior to merger announcement, stock prices commence a descent that continues through the next two days.
Informed traders, by definition (Easley, O’Hara and Srinivas, [2] ), gain by acting on privileged information. They use their knowledge of future price decreases to short sell sock, i.e. borrow stock, waiting till the price has declined, and then repay with cheaper stock. Borrowing occurs from institutional accounts and brokerage customer accounts as supported by Morck, Shleifer and Visny’s [3] finding that insider ownership of more than 25% was associated with increased short selling. Alternatively, they purchase put options or sell call options. With put purchases, the trader is purchasing the right to sell stock at a higher price than the market price. By selling call options on options that will not be exercised, the informed trader earns premiums. Liquidity traders trade to maintain an inventory of stock or in response to pressure from their clients. They may purchase stock that is losing value to obtain bargains or sell stock to avoid further losses. Their desire is not to profit from the merger announcement, but to hold a portfolio that achieves long-term growth (Abraham and Harrington [4] ). We construct a theoretical model that specifies that informed trader expectations of future stock prices as contained in short sale volumes and put purchase volumes form a lower bound while call sale volumes form the upper bound. The final stock price is set by stock sale volumes within these bounds. Additionally, we demonstrate that the liquidity traders of trading volume have such heterogeneous expectations of future stock prices that they set the final stock price with no bounds.
We extend the literature on trading responses to negative signals. Easley, O’Hara and Srinivas [2] theorized that upon receiving a negative signal, informed traders may sell calls or buy puts. They did not include profittaking by short sellers. We include short sale volumes as repositories of expectations of decreasing future stock prices. However, as short sale costs are high, short selling may terminate in a few rounds of trading so that the lower bound set by short sale volumes may be higher than that set by put buy volumes. This analysis is in accordance with observations of short selling at merger announcement by Mitchell, Pulvino and Stafford, [1] . Mitchell et al. [1] observed that informed traders short sold the acquirer stock in stock mergers and used the proceeds to purchase the target stock on the day before merger announcement. We recognize the role of liquidity traders in the trading environment. Our model incorporates trading by liquidity traders (usually institutional traders) in the form of stock and call option purchases, to purchase cheap stock and put purchases and stock sales to maintain liquidity. This is in accordance with Abraham and Harrington [4] who found that liquidity traders sell stock during the merger announcement period as measured by the decline in transaction costs from day −1 to day +2. Our inclusion of liquidity traders as market participants is in contrast to the perception in the literature that such traders are noise traders who are “willing to trade even though from an objective point of view they would be better off not trading” (Black [5] , p. 529). Most models of informed trading (Admati and Pfleiderer [6] ; Bamber, Barron and Stober [7] ) have suggested a tangential link between informed and liquidity trading. This study envisions a more direct link by placing both parties in the same trading environment.
The paper is organized into the following sections. Section 2 describes the impact of negative stimuli on informed trading with Section 2.1 explaining the lower bound based on short sale volumes and Section 2.2 explicating the lower bound based upon put buy volumes. Section 3 describes the establishment of final stock prices by informed traders with Section 3.1 on portfolio optimization with short selling and Section 3.2 on portfolio optimization with put buying. Section 4 is on the establishment of prices by liquidity traders. Finally, Section 5 provides conclusions.
2. The Impact of Negative Stimuli on Informed Trading
2.1. The Upper Bound
An informed trader, Trader 1, purchased call options on the acquirer stock prior to merger announcement with the expectation of forthcoming stock price increases. As stock prices commence their descent, Trader 1 sells calls at call bid prices. In the each round of trading, market makers adjust call bid prices at progressively lower levels as the value of call options shrinks with decreasing profitability of a call exercise strategy. Calls are typically purchased by call buyers who expect a reversal in the decline in stock prices, i.e. that the stock price of the acquirer stock will start rising again. They will continue to purchase calls as long as [Expected Stock Price − Exercise Price] > Call Premium, as this is the condition for profitability of exercise of a call option. The call premium increases in each round of trading in response to increasing demand for calls. It follows that call buyers will cease purchases of call options when the stock price falls sufficiently so that [Stock Price − Exercise Price] = Call Premium. At this point, call buyers will view further purchases of call options as increasingly unprofitable and cease buying. Trader 1 will no longer be in a position to sell calls and will cease trading.
 (1)
(1)
is an expression of the behavior of succinct intervals of the actual stock price V.  is the anticipated option price, O denotes option, x denotes optimistic Trader 1 evaluation, y denotes pessimistic Trader 1 evaluation and n denotes the number of informed trades with respect to time.
is the anticipated option price, O denotes option, x denotes optimistic Trader 1 evaluation, y denotes pessimistic Trader 1 evaluation and n denotes the number of informed trades with respect to time.
Trader 1 sells call options at the bid price in a market with falling actual and anticipated stock prices, V and 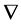 respectively. In successive rounds of trading, Trader 1 earns decreasing amounts of call premiums,
respectively. In successive rounds of trading, Trader 1 earns decreasing amounts of call premiums, 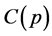 at progressively lower bid prices. In the final round of call selling, Trader 1 receives the minimum premium
at progressively lower bid prices. In the final round of call selling, Trader 1 receives the minimum premium 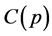 at time
at time 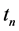 or
or . The incremental time period between the penultimate and final rounds of trading
. The incremental time period between the penultimate and final rounds of trading  describes the achievement of the minimum call premium. The actual stock price corresponding to the minimum call premium is the upper bound.
describes the achievement of the minimum call premium. The actual stock price corresponding to the minimum call premium is the upper bound.
 (2)
(2)
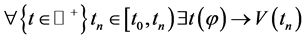 (3)
(3)
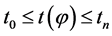 (4)
(4)
where
 call premium in the final round of trading, at time
call premium in the final round of trading, at time ;
;
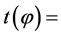 incremental difference in time between
incremental difference in time between  and
and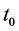 .
.
The upper bound is ultimately defined as the solution of the Fourier-Bessel function.
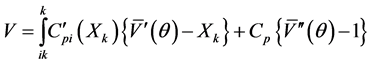 (5)
(5)
The orthogonality of the Fourier-Bessel function describes the upper bound where
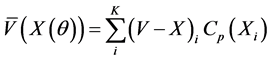 (6)
(6)
and
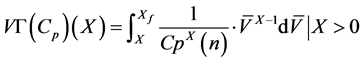 (7)
(7)
Let  can then be rewritten such that transparency can be lent to
can then be rewritten such that transparency can be lent to :
:
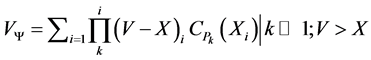 (8)
(8)
The upper bound was detected empirically in Abraham and Harrington’s [8] regression of call sale volumes on stock price changes on a sample of stock mergers from 2005-2007 in which call sale volume significantly reduced stock price changes 6 - 7 lags or 30 - 35 minutes after the release of the news about the stock merger .
.
2.2. The Lower Bound Based upon Short Sale Volumes
Informed traders meet their demand for stock with declining prices by short selling the acquirer stock. Trader 2 short sells stock by selling borrowed stock at a high price in the first round, then buying cheaper stock in the second round to repay the initial debt. This cycle is repeated in the third and fourth rounds of trading after which it ceases due to short-sale constraints. Short selling has been associated with restricted access to short-sale proceeds and insider prohibitions against short selling. Kosti and Pontiff [9] observed that 80% of mutual funds in their sample excluded short-sold stock. Trader 2’s expectation of stock price decreases is enshrined in the trading volume in Round 1. Market makers observe the demand for stock that is losing value, leading them to decrease stock bid prices. Stock that is borrowed in the second round of trading will have lower prices than those shorted in Round 1. More of this stock is borrowed in Round 2, as reflected in lower stock bid prices than Round. However, the aforementioned prevention of short selling after a few rounds ends short selling. If Trader 2’s demand for stock that is declining in value is satisfied, he or she will cease trading. However, another trader termed Trader 3 may represent the investor who seeks to obtain the greatest benefit from short selling, his or her short sale volume will contain the expectation of the maximum decrease in stock price due to short selling. The stock bid price corresponding to this final trading volume is the lower bound.
 (9)
(9)
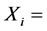 Number of shares short sold in Round 1;
Number of shares short sold in Round 1;
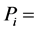 Sales price for shorted stock in Round 1;
Sales price for shorted stock in Round 1;
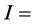 Interest expense to the short seller;
Interest expense to the short seller;
 Purchase price of shorted stock in Round 2.
Purchase price of shorted stock in Round 2.
Expression (9) outlines the trend of Trader 2’s infinitesimal return over a short interval. The negligible profit of the short seller for the i’th share of its corresponding j’th value tends to the depreciating end-of-day value. The interest rate I is trivial to the point of redundancy. Codependency of the share and its value along with the trivialization of I infers the number of shares for the final trade will be X (if nothing happens on the final day of trade this value is 1 and the entire equation is positive). The statement, thus, lends theoretical value to the gain of the short seller. We posit that the short seller’s gain is predicated on the time taken for the stock market to reach a constant (C) where the intervals of time are static but the number of static intervals reaches a tangible boundary. The integrated curl of the P trend within a time interval non-conducive to change lends objectivity to P.
Thus:
 (10)
(10)
Regulatory measures on the shares of Trader 3 set an irrational boundary that investors wish to make transparent. The fact that deregulation ends has little to do with post-regulation share values. The post-regulation boundary invites speculation about Trader 3’s perception of the market value. Thus the relationship between profitability prior to and post-regulation of short selling is tentatively greater than the actual price of the regulated stock.
2.3. The Lower Bound Based upon Put Buy Volumes
Let
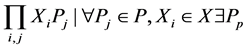 (11)
(11)
where
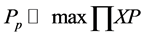 (12)
(12)
is a condition, then the following is implied
 (13)
(13)
We can propose an alternative method to arriving at the above generalized statement with the potential to disambiguate the final 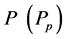 using a basic Fourier series:
using a basic Fourier series:
Let
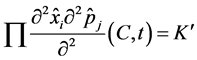 (14)
(14)
The general Fourier series indicates that
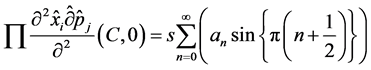 (15)
(15)
where s is a non-transparent dummy variable. If K' were transparent it would equal the right hand side of the equation and s would be a dividend. For some set of stocks purchased by Trader 2, the risk incurred by the investor is subject to constraint.
In the previous section, we defined Trader 3 as seeking the maximum benefit from short selling by repurchasing borrowed stock at the lowest price which in turn establishes the lower bound. This is the first lower bound. It is conceivable that Trader 3’s demand for stock that is decreasing in value is unsatisfied. This demand may be satisfied in the options market through the purchase of put options. Trader 3 may exercise put options by selling stock at a higher price than the prevailing market price, waiting for stock prices to decline in the next round of trading, purchase and then exercise more put options at a higher price than the market price and continue this pattern of trading until the gain on the put trade as depicted by Exercise Price − Stock Price < Put Premium. Diamond and Vereccchia [10] theorized that investors use put buying strategies to mitigate short-sale constraints. Danielson and Sorescu [11] empirically observed that the introduction of options results in trading shifting from short selling to put buying. The trader with the expectation of the greatest reduction in stock price below the exercise price will continue purchasing puts until he or she is the only put buyer, all others having satisfied their demand for negative volume and exited the market. The put buy volume of this trader in the final round of trading will contain the expectation that stock prices will decrease to their lowest level. Therefore, the stock price corresponding to this put bid price will be the second lower bound of the actual final stock price.
Empirically, Blau et al. [12] , observed that short-sale volumes for stocks with the most restrictive short-sale constraints contained greater predictability of stock returns than put-call ratios. This finding supports our contention that short sale volumes contain definite information about immediate stock prices. In contrast, put buying which may occur over several rounds of trading has less precise information about future stock prices.
3. The Establishment of Final Stock Prices by Informed Traders
Trading on the acquirer stock occurs in both the option and stock markets on the day prior to a stock merger announcement. At each round of trading in the stock market, traders sell or short sell acquirer stock. Market makers decrease ask prices so that the stock is sold at increasingly lower prices. Stock volumes reflect trader expectations of the extent to which the actual stock price < the forecasted stock price. We posit that stock volume represents the final price while option volume represents the bounds. Options buyers may seek higher returns by purchasing larger volumes of options while experiencing minimal loss in the event of non-exercise as option premiums are substantially lower than margined stock investments. We consider two cases. In the first case, short selling is permitted. In the second case, short selling is prohibited.
3.1. Portfolio Optimization with Short Selling
To recapitulate, Trader 2 sells the acquirer stock short until his or her demand for negative volume is met. His or her short sale volumes traded will reflect expectations of the lowest bid price for the stock. The bid price corresponding to the stock volume in the final round of trading is the final stock price for Trader 2. Other short sellers may be named Trader 2a, Trader 2b, or Trader 2c. Their trading volumes which are distinct from that of Trader 2 will set a range of final stock prices. For instance, Trader 2a’s short selling may be completed with a single transaction so that the market maker selling stock to Trader 2a reduces prices just once resulting in the final short sale occurring at a higher price than that of Trader 2. Given that such trading occurs on a single stock, and since investors hold portfolios of stocks, we employ the Elton et al. [13] formulation to specify the conditions for the creation of optimal portfolios with short selling. They define θ as the highest excess return to standard deviation of a stock. If Xi is the weight of each stock in the portfolio, the optimal portfolio will be a collection of stocks in different proportions (X values) such that  of the portfolio is maximized,
of the portfolio is maximized,
 (16)
(16)
Expression (16) may be expanded as follows:
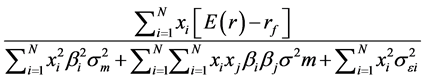 (17)
(17)
 Ratio of excess portfolio return above the risk-free rate to standard deviation of the portfolio;
Ratio of excess portfolio return above the risk-free rate to standard deviation of the portfolio;
 Expected return of a security;
Expected return of a security;
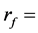 Risk-free rate of a security;
Risk-free rate of a security;
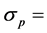 Standard deviation of the portfolio.
Standard deviation of the portfolio.
We subscribe to the Lintner [14] definition of short selling in which Xi may be capital gain which is negative of stock price appreciation. Each trader subjectively differentiates θ with respect to X so that each portfolio return is maximized at a different level of . In other words, different traders are satisfied with different levels of excess return to standard deviation. The stock price, Pn, corresponding to the excess return,
. In other words, different traders are satisfied with different levels of excess return to standard deviation. The stock price, Pn, corresponding to the excess return, 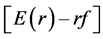 is the final optimal stock price for each trader.
is the final optimal stock price for each trader.
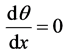 (18)
(18)
The first derivative of the numerator of (17) =
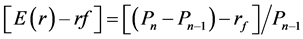 (19)
(19)
where
 Stock price in the final round of short selling at time
Stock price in the final round of short selling at time ;
;
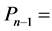 Stock price in the penultimate round of short selling at time
Stock price in the penultimate round of short selling at time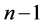 .
.
3.2. Portfolio Optimization with Put Buying
Trader 3 migrates to the options market purchasing put options on the acquirer stock. His or her put buy volumes traded will reflect expectations of the lowest bid (sale) price for the stock. The stock sale volumes for Trader 3’s counterparts in the stock market will set a range of final stock prices under the condition of no short selling. This is simply (10) with the stipulation that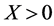 . Therefore, the final stock price = Pn, corresponding to the excess return,
. Therefore, the final stock price = Pn, corresponding to the excess return, 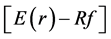 is the optimal stock price for each trader.
is the optimal stock price for each trader.
 (20)
(20)
The first derivative of the numerator of (17)
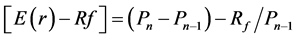 (21)
(21)
where
 Stock price in each round of put buying at time n which varies by stock trader;
Stock price in each round of put buying at time n which varies by stock trader;
 Stock price in the penultimate round of put buying at time
Stock price in the penultimate round of put buying at time .
.
4. Price-Setting by Liquidity Traders
Liquidity traders (typically, mutual funds) view stock that is continually decreasing in price over 3 days as either a buying opportunity for purchases of cheap stock or a selling opportunity to eliminate relatively weak performers while achieving positive long-term returns. Trading occurs primarily on days 1 - 5 following the merger. Abraham and Harrington [4] detected liquidity buying and selling during this time period by evaluating spreads. Market makers set spreads wide for informed traders and narrowed them for liquidity traders. Therefore, on days 1 - 2 spreads declined and completely vanished from days 3 - 5. We assume risk aversion with differing motivations for 1) liquidity selling volume and 2) liquidity buying volume. Adapting Friend and Blume’s [15] conceptualization of risk-aversion, we posit that both traders have risk-averse utility functions in which the first derivative of the utility of wealth is positive in the sense that utility increases with gains in wealth. Conversely, utility decreases with losses of wealth. However, the second derivative of the utility of wealth differs between the two traders. For traders who sell acquirer stock, the utility of wealth decreases with losses of stock values, or the second derivative of the utility of wealth is negative. For traders who purchase acquirer stock, the utility of wealth increases with losses of stock values, or the second derivative of the utility of wealth is positive.
For liquidity selling volume, Trader k is highly risk-averse to the extent of selling acquirer stock upon perceiving price declines. Friend and Blume [15] define  as the proportion of the net worth of an investor k placed in the portfolio of risky assets. We redefine
as the proportion of the net worth of an investor k placed in the portfolio of risky assets. We redefine  as equivalent to the weight of stock placed by this trader in a portfolio of risky assets. From Friend and Blume [15] ,
as equivalent to the weight of stock placed by this trader in a portfolio of risky assets. From Friend and Blume [15] ,
 (22)
(22)
where,
 Weight of stock in a portfolio of risky assets;
Weight of stock in a portfolio of risky assets;
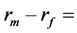 Market risk premium of stock;
Market risk premium of stock;
 Standard deviation of returns on a portfolio of risky assets;
Standard deviation of returns on a portfolio of risky assets;
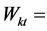 Wealth of trader k at time t contained in a portfolio of risky assets;
Wealth of trader k at time t contained in a portfolio of risky assets;
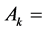 Arrow-Pratt coefficient of absolute risk aversion (Pratt [16] ); this is positive for Trader k
Arrow-Pratt coefficient of absolute risk aversion (Pratt [16] ); this is positive for Trader k
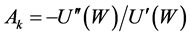
 Second derivative of the utility of wealth;
Second derivative of the utility of wealth;
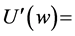 First derivative of the utility of wealth.
First derivative of the utility of wealth.
For liquidity buying volume, Trader l is less risk-averse than Trader k to the extent of purchasing acquirer stock upon perceiving price declines. Friend and Blume [15] define  as the proportion of the net worth of an investor l placed in the portfolio of risky assets. It is equivalent to the weight of stock placed by this trader in a portfolio of risky assets. From Friend and Blume [15] ,
as the proportion of the net worth of an investor l placed in the portfolio of risky assets. It is equivalent to the weight of stock placed by this trader in a portfolio of risky assets. From Friend and Blume [15] ,
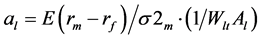 (23)
(23)
where,
 Weight of stock in a portfolio of risky assets;
Weight of stock in a portfolio of risky assets;
 Market risk premium of stock;
Market risk premium of stock;
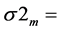 Standard deviation of returns on a portfolio of risky assets;
Standard deviation of returns on a portfolio of risky assets;
 Wealth of trader l at time t contained in a portfolio of risky assets;
Wealth of trader l at time t contained in a portfolio of risky assets;
 Arrow-Pratt coefficient of absolute risk aversion (Pratt [16] ); this is negative for Trader l
Arrow-Pratt coefficient of absolute risk aversion (Pratt [16] ); this is negative for Trader l

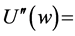 Second derivative of the utility of wealth;
Second derivative of the utility of wealth;
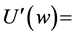 First derivative of the utility of wealth.
First derivative of the utility of wealth.
5. Conclusion
This paper creates a theoretical model that specifies that short sellers and put buyers trade in volumes that form the lower bound of future stock prices for acquirer stock that is continuously declining in value, while call sale volumes form the upper bound. The final stock price is set by stock sale volumes within these bounds. The trading volume of liquidity traders sets the final stock price with no bounds. We extend the literature on trading responses to negative signals by clarifying the role of short sale volumes in price-setting. Our model incorporates trading by liquidity traders (usually institutional traders) in the form of stock and call option purchases, to purchase cheap stock and put purchases and stock sales to maintain liquidity. Prior models of informed trading have suggested a tenuous link between informed and liquidity trading. This study envisions a more direct link by placing both parties in the same trading environment.