A Closed-Form Solution of a Kinetic Integral Equation for Rarefied Gas Flow in a Cylindrical Duct ()
1. Introduction
Research in the field of rarefied gas dynamics (RGD) involving the analysis and description of micro and nanoflows has been fundamental for the development of micro devices and new technologies, specially in the field of micro-electro-mechanical systems (MEMS) [1] -[5] .
The Boltzmann equation is the fundamental mathematical model for dealing with problems in RGD [6] . Investigations of its solution and associated kinetic models have found much attention in the last few years [7] - [13] . Numerical and analytical approaches have been developed, mainly in Cartesian coordinates [14] [15] .
The solution of Boltzmann-like problems is even more challenging in multidimensional and complex geome- tries, particularly, if one seeks for analytical approaches. In cylindrical coordinates, to overcome such difficulties, the integral form of the kinetic equations has been employed. In this context, several approaches have been proposed in the past years [16] - [19] , particularly related to the solution of the BGK model [20] , as, for example, the use of classical Legendre polynomials expansions [21] . A special approach used in an earlier work of Ferziger [22] , is based on a transformation proposed by Mitsis [23] , which allows us to recast the problem in cylindrical coordinates into a much simpler problem in plane Cartesian coordinates. The transformation, however, is restricted to some specific (simpler) physical cases.
Mitsis’ transformation [23] was used by Siewert and Valougeorgis [24] to develop a solution for the integral form of the S-model [25] kinetic equation, which is a vector equation, while the BGK kinetic equation is a scalar problem. It has been addressed in the literature, however, that the S-model is more appropriate than the BGK model to deal, for instance, with nonisothermal flows [24] [26] .
In this work, we use an spectral approach based on Hermite cubic splines expansions along with a collocation scheme to solve the vector integral form of the S-model kinetic equation for flow in cylindrical tube. Numerical results are obtained for the Poiseuille and thermal-creep problems. As in other analytical approaches [24] the solution is explicit, in terms of the spatial variable. However, the technique proposed in this work, that has been also effective to deal with the BGK integral equation [27] , may be extended to deal with the problems which include reflexive boundary conditions.
2. The formulation
The initial formulation of the problems we treat in this work, is the integro-differential formulation associated with the kinetic S-model [24] , for describing the behavior of gas flows in a cylindrical tube of radius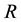 , with no variation in the axial direction, such that the distribution of particles and the boundary conditions depends on the spatial variable
, with no variation in the axial direction, such that the distribution of particles and the boundary conditions depends on the spatial variable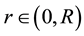 , written in dimensionless units, and the particle velocity vector
, written in dimensionless units, and the particle velocity vector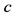 , also given in dimensionless units, expressed in the cylindrical coordinates. Still, in the initial formulation, the flow is subject to reflexive boundary conditions at
, also given in dimensionless units, expressed in the cylindrical coordinates. Still, in the initial formulation, the flow is subject to reflexive boundary conditions at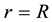 . In Ref. [24] , the authors follow a previous derivation regarding to the BGK model [28] to derive in details the integral form of the equation for the S-model, which describes the flow of a rarefied gas in a straight cylindrical duct of radius
. In Ref. [24] , the authors follow a previous derivation regarding to the BGK model [28] to derive in details the integral form of the equation for the S-model, which describes the flow of a rarefied gas in a straight cylindrical duct of radius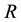 , which will be our starting point of this work. Since the derivations were done in details in [24] [28] , we do not repeat it here. We start, already, from considering the integral vector equation [24]
, which will be our starting point of this work. Since the derivations were done in details in [24] [28] , we do not repeat it here. We start, already, from considering the integral vector equation [24]
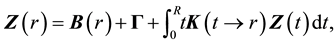 (1)
(1)
for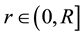 . In Equation (1) the inhomogeneous term
. In Equation (1) the inhomogeneous term  is given by
is given by
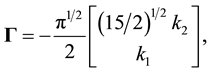 (2)
(2)
where the constants 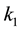 and
and 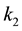 are defined so that
are defined so that 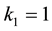 and
and 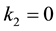 for the so-called problem of Poiseuille flow while
for the so-called problem of Poiseuille flow while 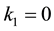 and
and 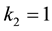 for the thermal-creep problem. Still, the kernel of integral equation is
for the thermal-creep problem. Still, the kernel of integral equation is
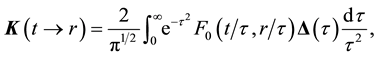 (3)
(3)
where
![]() (4)
(4)
and
![]() (5)
(5)
Here ![]() and
and ![]() are the modified Bessel functions of zero order, first and second kind [29] , respectively. Furthermore, in Equation (3),
are the modified Bessel functions of zero order, first and second kind [29] , respectively. Furthermore, in Equation (3),
![]() (6)
(6)
with
![]() (7)
(7)
![]() (8)
(8)
and
![]() (9)
(9)
Now, if we define [24] ,
![]() (10)
(10)
we can evaluate the quantities of physical interest for the gas flow, such as the velocity profile [24]
![]() (11)
(11)
and the heat-flow profile
![]() (12)
(12)
Consequently, we write the particle-flow rate as
![]() (13)
(13)
and the heat-flow rate
![]() (14)
(14)
The Equations (11) to (14) are used for both problems, Poiseuille and thermal-creep, depending on the specified values of the constants ![]() and
and ![]() which define the expression used for the source term given in Equation (2).
which define the expression used for the source term given in Equation (2).
Finally, we note that, in Equation (1), the term ![]() brings the information from the boundary condition, and it is not really an inhomogeneous term when reflexive boundary conditions are applied. For this reason, the only case considered in Ref. [24] was the diffuse reflection, where, at the end
brings the information from the boundary condition, and it is not really an inhomogeneous term when reflexive boundary conditions are applied. For this reason, the only case considered in Ref. [24] was the diffuse reflection, where, at the end![]() . At this point, in this work, we also disregard this term in our formulation and will comment on that later on in this text.
. At this point, in this work, we also disregard this term in our formulation and will comment on that later on in this text.
3. The solution
Firstly, we rewrite Equation (1) as,
![]() (15)
(15)
for![]() ,
, ![]() and for the case with no specular reflection,
and for the case with no specular reflection,![]() .
.
We then propose a solution to Equation (15) in terms of a truncated expansion of Hermite cubic splines functions [30] , as
![]() (16)
(16)
where ![]() are vectors
are vectors
![]() (17)
(17)
whose components (constants) ![]() and
and ![]() are to be determined. In regard to the splines functions
are to be determined. In regard to the splines functions![]() ,
,
first of all, we consider there to be ![]() knots
knots ![]() defined on the interval
defined on the interval![]() , such that
, such that ![]()
(see Appendix for details).
If we now substitute Equation (16) into Equation (15) we obtain
![]() (18)
(18)
which still can be expressed in the form
![]() (19)
(19)
with
![]() (20)
(20)
and
![]() (21)
(21)
At this point, we introduce a collocation scheme, such that, if we evaluate Equation (19) at the collocation points
![]() (22)
(22)
we end up with
![]() (23)
(23)
for![]() , which is a
, which is a ![]() linear system to the constants
linear system to the constants ![]() and
and ![]() used in expansion
used in expansion
given by Equation (16).
4. Computational Aspects
The procedure described in Section 3 may be considered quite straightforward. However the solution of the
linear system given by Equations (23), depends on the explicit evaluation of the integrals ![]() and
and
![]() , which are written in terms of the kernel, Equations (3) to (9), which clearly includes singularities
, which are written in terms of the kernel, Equations (3) to (9), which clearly includes singularities
that introduce numerical difficulties. In this way, a series of computational steps have to be taken into account.
As a first step, as used in previous works [24] [31] , for computational reasons, the modified Bessel functions are rewritten as
![]() (24)
(24)
such that Equations (4) and (5) are now expressed as
![]() (25)
(25)
for ![]() and
and
![]() (26)
(26)
for![]() . To be consistent, from now on, we consider the previously given integral equation kernel, Equation (3), expressed in the form
. To be consistent, from now on, we consider the previously given integral equation kernel, Equation (3), expressed in the form
![]() (27)
(27)
Continuing, if we look back to Equations (6) to (9), we can see that
![]() (28)
(28)
with
![]() (29)
(29)
![]() (30)
(30)
and
![]() (31)
(31)
where, again, the (constant components) matrices![]() ,
, ![]() ,
, ![]() are defined in Equations (7) to (9). More importantly, in writing the kernel as above, it is to point out that in these definitions, the only expression which effectively involves the term
are defined in Equations (7) to (9). More importantly, in writing the kernel as above, it is to point out that in these definitions, the only expression which effectively involves the term ![]() which induces a singular behavior, is the first one in the right hand-side. We note, however, that this same expression was part already of the BGK model kernel we had to deal in a previous work [21] .
which induces a singular behavior, is the first one in the right hand-side. We note, however, that this same expression was part already of the BGK model kernel we had to deal in a previous work [21] .
Finally, for future use, later on in this text, we can also express the kernel of the integral equation, in a matrix form,
![]() (32)
(32)
following, of course, the previous definitions given in Equations (7) to (9) and Equations (29) to (31). Here,
![]() (33)
(33)
![]() (34)
(34)
and
![]() (35)
(35)
Going back to the definition of the linear system we need to solve, Equations (23), we now focus our
attention in the definition of the functions ![]() and
and ![]() given in Equations (20) and (21).
given in Equations (20) and (21).
Considering that ![]() is the support of the spline function
is the support of the spline function![]() , in other words,
, in other words, ![]() ,
,
we note that
![]() (36)
(36)
if ![]() and
and
![]() (37)
(37)
if ![]() with
with
![]() (38)
(38)
In an analogous form,
![]() (39)
(39)
if ![]() and
and
![]() (40)
(40)
if ![]() with
with
![]() (41)
(41)
In fact, to be more specific, we can express the vector![]() , in terms of its components
, in terms of its components
![]() (42)
(42)
such that
![]() (43)
(43)
and
![]() (44)
(44)
where ![]() and
and ![]() are the constants to be defined in the proposed expansion, Equation (16), obtained as the solution of the linear system Equations (23). The terms
are the constants to be defined in the proposed expansion, Equation (16), obtained as the solution of the linear system Equations (23). The terms![]() , for
, for![]() , are defined in terms of expressions
, are defined in terms of expressions ![]() given in Equations (33) to (35),
given in Equations (33) to (35),
![]() (45)
(45)
if ![]() and
and
![]() (46)
(46)
if![]() . Similarly, the vector
. Similarly, the vector![]() , defined by Equations (39) and (40), is rewritten in a matrix form
, defined by Equations (39) and (40), is rewritten in a matrix form
![]() (47)
(47)
with
![]() (48)
(48)
and
![]() (49)
(49)
Here
![]() (50)
(50)
if ![]() and
and
![]() (51)
(51)
if![]() . Considering the explicit derivations above, at this point, we can rewrite the linear system defined in Equations (23), in the following form
. Considering the explicit derivations above, at this point, we can rewrite the linear system defined in Equations (23), in the following form
![]() (52)
(52)
and
![]() (53)
(53)
for![]() , where
, where
![]() (54)
(54)
for![]() ,
, ![]() and
and ![]() are given by the expressions shown in Equations (41)-(46) and
are given by the expressions shown in Equations (41)-(46) and
(50)-(51). Still, the terms ![]() and
and ![]() are defined by the components of the source term
are defined by the components of the source term![]() , so that
, so that
![]() (55)
(55)
and
![]() (56)
(56)
depending on the problem, as mentioned earlier: ![]() and
and ![]() for the Poiseuille flow;
for the Poiseuille flow; ![]() and
and ![]() for the thermal-creep problem.
for the thermal-creep problem.
The linear system given by Equations (52) and (53), is of order ![]() (or
(or![]() , which solution, the constants
, which solution, the constants ![]() and
and![]() , allow us to evaluate the quantities of physical interest such as velocity profile
, allow us to evaluate the quantities of physical interest such as velocity profile
![]() (57)
(57)
and the heat flow profile
![]() (58)
(58)
Numerical quadrature schemes
Searching for a general procedure, as much as possible, the basic approach for evaluating the integrals involved in this derivation was based on the use of the Gauss-Legendre quadrature scheme [29] with nodes ![]() and weights
and weights ![]() defined in the interval
defined in the interval![]() . In this form, convenient mappings, according to the integration interval, were used.
. In this form, convenient mappings, according to the integration interval, were used.
In this way, we define
![]() (59)
(59)
and we consider a quadrature scheme with ![]() nodes and weights for evaluating the integrals defined in Equations (27) to (29) as
nodes and weights for evaluating the integrals defined in Equations (27) to (29) as
![]() (60)
(60)
![]() (61)
(61)
and
![]() (62)
(62)
At this point, however, a special remark has to be done in regard to the evaluation of Equation (60). While
the general procedure described above works well as long as ![]() is not small―in fact, using
is not small―in fact, using ![]()
one obtains results which agree in seven digits with results obtained by the software Maple―the case ![]() has to be treated more carefully, if ones search for more accurate results as a general case.
has to be treated more carefully, if ones search for more accurate results as a general case.
To deal with that, we subtract (and add) from Equation (29) the expression
![]() (63)
(63)
In the resulting integral expression, we introduce the change of variables
![]() (64)
(64)
and, subsequently, once more, we add (and subtract) the integral term
![]() (65)
(65)
To be clear, when ![]() (we considered typically
(we considered typically![]() ) we evaluate
) we evaluate ![]() as
as
![]() (66)
(66)
with
![]() (67)
(67)
and
![]() (68)
(68)
The reasons for doing that is, firstly, the use of these additional functions results in a smoother function when approaching![]() . In addition to that,
. In addition to that, ![]() can be expressed as
can be expressed as
![]() (69)
(69)
where ![]() is the elliptic integral of the first order, that can be evaluated numerically by applying the algorithm given by [29] . Still,
is the elliptic integral of the first order, that can be evaluated numerically by applying the algorithm given by [29] . Still, ![]() , can be evaluated by using Maple, such that
, can be evaluated by using Maple, such that![]() . The integral
. The integral![]() , given by Equation (67), can be then evaluated without much difficulty by applying the scheme of Gauss-Legendre quadrature, by mapping
, given by Equation (67), can be then evaluated without much difficulty by applying the scheme of Gauss-Legendre quadrature, by mapping ![]() into
into![]() .
.
Therefore, in regard to the computational scheme, we note that ![]() is evaluated either by Equation (60) if
is evaluated either by Equation (60) if ![]() or Equation (66), if
or Equation (66), if![]() . This procedure is, in fact, analogous to the one we used to deal with the BGK model [21] [27] and it was implemented once we seek for increasing the accuracy of the final results, as we will comment later on in this text.
. This procedure is, in fact, analogous to the one we used to deal with the BGK model [21] [27] and it was implemented once we seek for increasing the accuracy of the final results, as we will comment later on in this text.
To all other integrations processes needed in this formulation, more specifically, the expressions given by Equations (46) and (51) as well as Equations (13) and (14), linear mappings from the integration interval to the interval ![]() were performed, to the use of the Gauss-Legendre quadrature scheme. Clearly, in the case of Equations (46) and (51) the dependence of the integration limits on the interval definition of the splines functions have to be taken into account to improve the computational results. In this way, we evaluate these equations as
were performed, to the use of the Gauss-Legendre quadrature scheme. Clearly, in the case of Equations (46) and (51) the dependence of the integration limits on the interval definition of the splines functions have to be taken into account to improve the computational results. In this way, we evaluate these equations as
![]() (70)
(70)
if ![]() and
and
![]() (71)
(71)
if![]() . Here we used
. Here we used
![]() (72)
(72)
![]() (73)
(73)
![]() (74)
(74)
and
![]() (75)
(75)
With this, we conclude the evaluation of the elements of the system given by Equations (52) and (53).
5. Numerical results
As input data in our program we need to specify the radius of the duct, ![]() , the order of the quadrature schemes
, the order of the quadrature schemes ![]() and the number
and the number ![]() of knots (associated to the splines functions) which will define
of knots (associated to the splines functions) which will define ![]() in the linear system given by Equations (52) and (53). We implemented a FORTRAN program and subroutines from LINPACK [32] were used to solve the linear system. The solution was then used to obtain the physical quantities of interest, the velocity and heat-flow profiles, Equations (57) and (58), and subsequently Equations (13) and (14).
in the linear system given by Equations (52) and (53). We implemented a FORTRAN program and subroutines from LINPACK [32] were used to solve the linear system. The solution was then used to obtain the physical quantities of interest, the velocity and heat-flow profiles, Equations (57) and (58), and subsequently Equations (13) and (14).
As a first test, to check and to have confidence in our approach, we reproduced all the results listed in Ref. [24] , for the velocity and heat-flow profiles (case![]() ), as well as velocity slips and particle flow rates for values of
), as well as velocity slips and particle flow rates for values of ![]() ranging from
ranging from ![]() to
to![]() . We do not repeat the results here since they were already reported in [24] .
. We do not repeat the results here since they were already reported in [24] .
As we mentioned earlier, the approach used in that work can be very accurate, since it works with a Cartesian coordinates problem associated with a very accurate discrete ordinates solution, after using Mitsis’ transfor- mation [23] . In order to get agreement in six to seven digits, for all cases, with Siewert and Valougeorgis’ results
(listed with seven digits) [24] , we used![]() ,
, ![]() ,
, ![]() and
and![]() , for
, for
![]() to
to![]() . If we use, for instance, lower order approximations as
. If we use, for instance, lower order approximations as![]() ,
, ![]() ,
,
![]() and
and ![]() results can also be reproduced, in general, with two to three digits of agreement with [24] , particularly for
results can also be reproduced, in general, with two to three digits of agreement with [24] , particularly for![]() .
.
We then investigated additional cases. To provide the results we list in Table 1 and Table 2, we used the first set of parameters listed above. In regard to Table 2, we remark that, the Onsager reciprocity relation [33] [34] , ![]() is verified. Still, the results listed in Table 2 have some agreement with Ref. [26] , within the accuracy
is verified. Still, the results listed in Table 2 have some agreement with Ref. [26] , within the accuracy
![]()
Table 1. Velocity and heat flow profiles in a duct with R = 1.
declared in that paper (0.5%). In addition to provide accurate results, it is important to remark that, the approa- ch proposed in this work may be used to simulate the case which includes specular reflection at the surface![]() , as we show in a subsequent work, and, a better description of the boundary effects is a relevant issue when it comes to the modeling of microflows.
, as we show in a subsequent work, and, a better description of the boundary effects is a relevant issue when it comes to the modeling of microflows.
6. Conclusion
In this work, we have used a classical spectral approach, based on the use of Hermite cubic splines combined with a collocation scheme, to obtain a solution, in a closed-form, to the S-model kinetic integral vector equation relevant to describe rarefied gas flow in cylindrical coordinates. The main purpose of this work was to verify the performance of this approach as an extension of an earlier work related to a simpler integral model equation, the BGK model, trying to derive, as much as possible, a general approach which can be now, in a subsequent work, extented to include the treatment of reflexive boundary conditions. The numerical results obtained showed good agreement with accurate results available in the literature.
Acknowledgements
The authors would like to thank CNPq of Brazil for partial financial support of this work. One of the authors (LBB) would like to thank the Mathematics Department of North Carolina State University for the kind hospitality during a visit when this work was written.
Appendix
The Spline Functions
We follow here the Hermite cubic splines functions as defined by Schultz [30]. In this way, we first consider the ![]() knots
knots![]() , defined in the interval
, defined in the interval ![]() as,
as,
![]() (76)
(76)
where, in this work, we use![]() . To express a function
. To express a function![]() , for
, for![]() , in terms of the spline functions, we write
, in terms of the spline functions, we write
![]() (77)
(77)
where ![]() are constants to be determined and
are constants to be determined and![]() . In fact, associated with each one of the knots, there are two spline functions
. In fact, associated with each one of the knots, there are two spline functions![]() , which are defined differently for even or odd values of
, which are defined differently for even or odd values of![]() ,
,
![]() (78)
(78)
for![]() . Here, we introduce
. Here, we introduce
![]() (79)
(79)
![]() (80)
(80)
and we consider that the spline functions are zero unless otherwise, to write
![]() (81)
(81)
![]() (82)
(82)
for![]() , and
, and
![]() (83)
(83)
Similarly, we write
![]() (84)
(84)
![]() (85)
(85)
for![]() , and
, and
![]()
(86)