1. Introduction
1.1. Aims and Scope
The purpose of this paper is to show that, if the mass density is assumed uniform within the core (nucleus or bulge) of a spiral galaxy, then, by Newtonian Mechanics and Euclidean Geometry, the mass density in the shell (the domain outside of the core containing the galactic disk) must vary as the inverse square of radial distance, while the angular velocity in this domain remains inversely proportional to radial distance, if the core-shell interface is sharply defined. These distributions of matter, in turn, will allow the equations of movement for the core and shell disks (perpendicular to the axis of rotation) to be derived and although these equations do not lead to spiral trajectories nevertheless any radial line of material points crossing the shell and passing through the core centre will be distorted, it will be shown, into a symmetric pair of spirals of Archimedes. It will be shown, moreover, that the bar portion within the core remains undistorted and merely rotates. We begin with some recent high resolution spectrographic observations.
1.2. Relevant Observations
There are two kinds of reliable observation that can be made on a spiral galaxy. The first is obtained from galaxies that present edge-on and the second from those spiral galaxies that we see face-on.
If the slit of a long-slit spectroscope is aligned with the disk of a spiral galaxy that presents edge-on, in the field of view of a telescope, the lines of the resulting spectrum appear distorted, since the upper portion of each spectral line is moved towards the high frequency end of the spectrum, if the mass in the upper portion of the galactic disk moves towards the observer, and vice versa for the lower portion of each spectral line. The Doppler shifts corresponding to these distortions therefore provide the circumferential velocity distributions in the galaxies concerned. The spectral lines have been found [1] -[3] to suffer distortions as in Figure 1 and the prototypes of this case are F568-3 and UGC 4325. It is with this type of spiral galaxy that we shall be concerned here.
The results of McGaugh, Rubin and Blok [1] for the edge-on galaxy F568-3 show that the circumferential velocity is proportional to radial distance from the axis of rotation out to a radius of about 14 seconds of arc. This marks the boundary to the core where an abrupt change occurs to a constant velocity of circulation of about 110 k∙ms−1. These results support earlier measurements by Swaters, Madore and Trewhella [2] .
Early measurements on M31, or NGC 224 (The Great Nebula in Andromeda), also show a central region within which circumferential velocity is close to proportional to radial distance, while again the velocity of circulation in the shell is constant. But there is a small region near the axis of rotation marked by substantial departures from linearity [4] -[6] .
2. Analytical Principles
Figure 2 represents a hypothetical sphere of identical mass-points distributed with uniform density and intended to correspond to the core of a spiral galaxy of the type under consideration. The plane, C, at the centre, perpendicular to the axis of rotation, is the core disk (the central disk perpendicular to the axis of rotation) as opposed to the shell disk (the outer disk perpendicular to the rotation axis).
Let r denote the position vector of a mass-point within the core. Then, as shown in works on potential theory. the material in the domain outside of r, if the distribution is assumed to be spherically symmetric, contributes nothing to the gravitational force acting on a point-mass m at radial distance r (Appendix A). The force of gravity on such a mass is directed to the centre O of the plane C (Figure 2) and equals  where
where

Figure 1. Distortion to spectral lines found for edge-on galaxies such as F 568-3 and UGC 4325.

Figure 2. A stylized, spherically symmetric, pointmass distribution. The central plane, C, rotates in the same fashion as a phonograph turntable.
 is the mass within
is the mass within  and G is the universal constant of gravity. This force is balanced by the centrifugal force due to rotation, but the angular velocity is low so that the assumption of spherical symmetry remains valid both for the core and the shell.
and G is the universal constant of gravity. This force is balanced by the centrifugal force due to rotation, but the angular velocity is low so that the assumption of spherical symmetry remains valid both for the core and the shell.
We have, for equilibrium in any plane parallel to C (planes perpendicular to the axis of rotation),
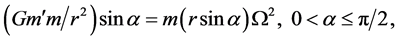 (2.1)
(2.1)
where 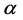 is the angle that r makes with the axis of rotation and
is the angle that r makes with the axis of rotation and  is the magnitude of the angular velocity with which the mass point, m, revolves about the axis.
is the magnitude of the angular velocity with which the mass point, m, revolves about the axis.
We now introduce the fundamental:
Hypothesis 2.1 The mass density is uniform within the core.
Under this hypothesis it follows that
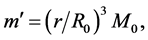
where  is the total mass of the core and
is the total mass of the core and 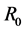 is its radius. Substituting in Equation (2.1) for
is its radius. Substituting in Equation (2.1) for 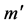 we get
we get
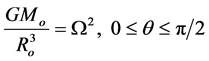 (2.2)
(2.2)
leading to
 (2.3)
(2.3)
for the square of the circulation velocity,  at the outer edge of the core disk, C. This, it will be shown, is also the velocity of circulation in the shell disk. The equation seems to be well known. Equation (2.2) gives the same angular velocity for all points of the core and the disk rotates in the same fashion as the turn-table of a phonograph. Thus have we proved:
at the outer edge of the core disk, C. This, it will be shown, is also the velocity of circulation in the shell disk. The equation seems to be well known. Equation (2.2) gives the same angular velocity for all points of the core and the disk rotates in the same fashion as the turn-table of a phonograph. Thus have we proved:
Theorem 2.1 If within a rotating spherical body of mass-points, constrained by gravity and inertia alone, the mass density is uniform then the central disk, perpendicular to the axis of rotation in that body, rotates in the same manner as a rigid disk.
The period of revolution of a point-mass anywhere in the core is 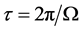 and, from Equation (2.2), we obtain the formula giving the mass density,
and, from Equation (2.2), we obtain the formula giving the mass density,  in the core
in the core
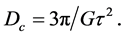 (2.4)
(2.4)
It follows that every point-mass within C orbits the axis of symmetry with the same period. This period is given by
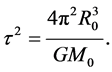 (2.5)
(2.5)
A point-mass not on the plane C of Figure 2 will also orbit the axis of symmetry with the above period, as already shown (Equations (2.1) and (2.2)), but must move, at the same time, relative to the plane C, due to the gravitational attraction of matter on the opposite side of C.
The component of the gravitational force perpendicular to the plane C, on a unit point-mass anywhere in the core, is (Figure 2)
 (2.6)
(2.6)
where z is the distance of the point above the plane C. Therefore
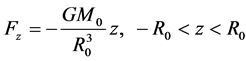 (2.7)
(2.7)
or, from Equation (2.2),
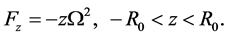 (2.8)
(2.8)
We therefore have for equilibrium in a direction perpendicular to the plane C
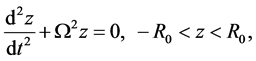 (2.9)
(2.9)
which is the equation of simple harmonic motion. The solution to this equation is
 (2.10)
(2.10)
where Z is the maximum value of z reached by the point-mass in its path.
3. Forces in the Core
3.1. Equation of Movement
Since the plane C in the core can be regarded as a rotating rigid disk we have, from Equation (B.9), if 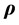 is the position vector of a point-mass in the plane C and V is its vectorial velocity [7] -[9] ,
is the position vector of a point-mass in the plane C and V is its vectorial velocity [7] -[9] ,
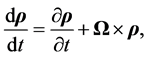 (3.1)
(3.1)
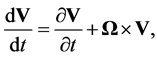 (3.2)
(3.2)
where
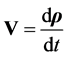 (3.3)
(3.3)
and d/dt denotes the total rate of change due to rotation of the axes fixed on C as well as changes relative to C, while  is the rate of change with the time, referred to C, as if the disk were stationary. The operator
is the rate of change with the time, referred to C, as if the disk were stationary. The operator  as used here, only has meaning when applied to a vector and in the case of a scalar quantity must be replaced by d/dt.
as used here, only has meaning when applied to a vector and in the case of a scalar quantity must be replaced by d/dt.
The equation of movement of a point-mass, m, in the core is, by Newton’s second law,
 (3.4)
(3.4)
where 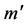 is the mass inside the radius
is the mass inside the radius  since the mass outside of this radius cannot make any contribution to the gravitational force on m (Appendix A).
since the mass outside of this radius cannot make any contribution to the gravitational force on m (Appendix A).
From our Hypothesis 2.1
 (3.5)
(3.5)
and from Equations (3.4) and (2.2) we now obtain for the core
 (3.6)
(3.6)
Substituting from Equation (3.2) we therefore have
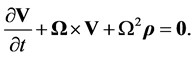 (3.7)
(3.7)
From Equations (3.3) and (3.6)
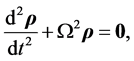 (3.8)
(3.8)
while from Equations (3.1)-(3.3)
 (3.9)
(3.9)
and, since
 (3.10)
(3.10)
and 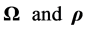 are perpendicular vectors, we have
are perpendicular vectors, we have
 (3.11)
(3.11)
whence, by Equation (3.8), we obtain the equation of movement of a point mass in the core
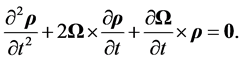 (3.12)
(3.12)
3.2. Conservation of Angular Momentum within the Core
From Equation (3.8) we obtain the condition
 (3.13)
(3.13)
and since
 (3.14)
(3.14)
it follows, from Equation (3.13), that
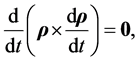 (3.15)
(3.15)
which leads to
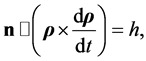 (3.16)
(3.16)
where h equals a constant and n is the unit vector normal to the core disk. The vector n is assumed here to be fixed. The area of the triangle traced out by the arm 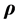 in time
in time  equals
equals 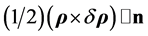 so that h/2 is the areal velocity. But from Equation (3.1)
so that h/2 is the areal velocity. But from Equation (3.1)
 (3.17)
(3.17)
and since (see Equation (3.10)) 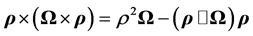 and since
and since  are perpendicular we get, from the two equations above,
are perpendicular we get, from the two equations above,
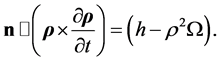 (3.18)
(3.18)
This equation describes the areal velocity as observed from within the rotating frame on C and should be compared to Equation (3.16) which applies relative to fixed external axes. A further illustration of this feature of the transformation from fixed to rotating frames is revealed by the following argument.
We choose the unit vector t tangential to the trajectory of a point mass on C (Figure 3) and, as above, n normal to the core disc so that (t, n, b) form a right-handed set. The components of the position, velocity and acceleration vectors relative to the rotating frame are [7] (these may be obtained from Equation (B.9)), if  is the angle that the radius vector makes with some fixed radial direction on C,
is the angle that the radius vector makes with some fixed radial direction on C,
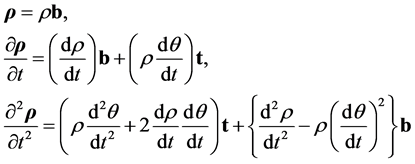 (3.19)
(3.19)
and substituting into Equation (3.12), again neglecting the precession term, we obtain, for the t-component,
 (3.20)
(3.20)
This ordinary differential equation may be solved by separation of variables, leading to
 (3.21)
(3.21)
where h again equals twice the areal velocity, as observable from an external fixed frame. Relative to fixed external axes, in contrast, we obtain from Equation (3.8), the well known relation
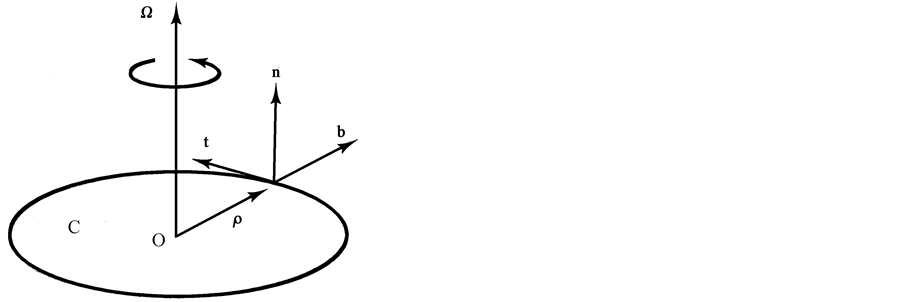
Figure 3. Turntable with embedded unit vectors (t, n, b).
 (3.22)
(3.22)
4. The Shell
4.1. Angular Velocities and Mass Density Distributions
Dark matter [10] was originally perceived as material with which we are familiar, but which emits levels of light flux comparable to the cosmological background black body radiation. The idea was invented to explain the odd mechanical behaviour of certain clusters of galaxies [11] [12] and such cold material may be assumed to surround galactic disks to form the major part of each shell. But distinctly unscientific ideas have crept in and, in the interests of precision, dark matter will be referred to here as cold-matter.
From Newton’s law of gravity, if 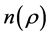 is the local angular velocity in the shell disk, where again
is the local angular velocity in the shell disk, where again  is radial distance from the axis of rotation, we have, equating the gravitational and centrifugal forces acting on a point-mass,
is radial distance from the axis of rotation, we have, equating the gravitational and centrifugal forces acting on a point-mass,
 (4.1)
(4.1)
where 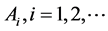 are constants,
are constants, 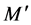 is the mass inside radius
is the mass inside radius  R is the effective outside radius of the shell and it has been assumed that we may expand
R is the effective outside radius of the shell and it has been assumed that we may expand 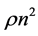 in powers of
in powers of  Therefore
Therefore
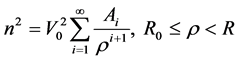 (4.2)
(4.2)
and
 (4.3)
(4.3)
It will now be shown that the mass density, 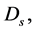 in the shell must vary as the inverse square of the radial distance;
in the shell must vary as the inverse square of the radial distance;
 (4.4)
(4.4)
where  equals a constant.
equals a constant.
For the mass 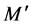 of hot-and cold-matter inside the radius
of hot-and cold-matter inside the radius  we have
we have
 (4.5)
(4.5)
and by Equation (4.3) this leads to
 (4.6)
(4.6)
This equation can be satisfied if  and
and
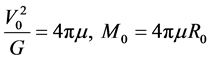 (4.7)
(4.7)
from which we get, on eliminating 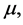
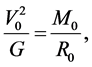 (4.8)
(4.8)
which is the same as Equation (2.3). Equation (4.4) is therefore sound, being entirely consistent with our hypothesis 2.1. By Equation (4.4) and the second of Equation (4.7), moreover,
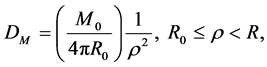 (4.9)
(4.9)
while Equations (4.2) and (4.3) lead to
 (4.10)
(4.10)
The total mass of hotand cold-matter within both the core and the shell, out to the radial distance 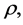 is, by Equation (4.9), therefore given by
is, by Equation (4.9), therefore given by
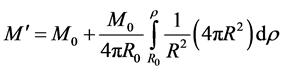 (4.11)
(4.11)
or
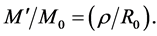 (4.12)
(4.12)
From these results we have:
Theorem 4.1 In a hypothetical spherically symmetric shell of mass-points surrounding a rotating spherically symmetric core of mass-points, constrained only by gravitation and inertia and in which the mass density remains uniform, the mass density in the shell diminishes with the inverse square of radial distance, while the angular velocity in the shell diminishes inversely with radial distance from the axis of rotation.
We also have by Equation (4.12) the:
Corollary 4.1 The ratio of total mass within any given radius in the shell to that of the core equals the ratio of that radius to the core radius.
4.2. Spirals on the Shell Annulus
From the first of Equation (4.10) it is clear that the circumferential velocity in the shell is constant and independent of  a fact to which abundant observational evidence testifies.
a fact to which abundant observational evidence testifies.
If therefore we draw two concentric circles mark a common diameter and then also mark off equal lengths along the circumferences of these two circles, starting from points on the common diameter, we will have located two points on the distorted diameter. In this way, using a number of concentric disks of different diameters, the entire curve into which the bar becomes distorted as, well as its progress, may be viewed.
But if we consider two concentric circles of radii  on the outer shell disk we get, on equating equal lengths along their circumferences and letting
on the outer shell disk we get, on equating equal lengths along their circumferences and letting 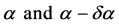 equal the angles subtended by the ends of the two equal length elements
equal the angles subtended by the ends of the two equal length elements
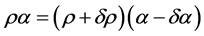 (4.13)
(4.13)
which leads to
 (4.14)
(4.14)
This ordinary differential equation may be solved by separation of variables, which leads to
 (4.15)
(4.15)
where A equals a constant. If we now change the line-origin from which the polar angle  is measured we get
is measured we get
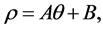 (4.16)
(4.16)
where B equals a constant, and this equation, and Equation (4.15) describe Archimedean spirals.
4.3. Potentials in the Core and Shell
The gravitational potential at a point in the outer shell will be defined here as the work done to move a unit point-mass from the specified point in the shell to an infinite distance from the core centre. Denoting this potential by V we obtain
 (4.17)
(4.17)
where  is the total mass inside the radius
is the total mass inside the radius  M is the total mass of the galaxy and R is its effective outer radius. Substituting for
M is the total mass of the galaxy and R is its effective outer radius. Substituting for 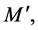 from Equation (4.12), we obtain
from Equation (4.12), we obtain
 (4.18)
(4.18)
so that , by Equation (2.2)
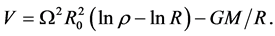 (4.19)
(4.19)
From Equation (3.6) we have, as the equation of movement for a mass-point in the shell referred to external fixed axes, noting that angular velocity, n, is now a function of 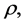
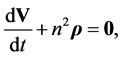 (4.20)
(4.20)
or, by Equation (3.3),
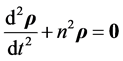 (4.21)
(4.21)
and, taking the scalar product with 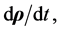 we get,
we get,
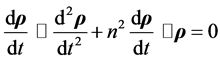 (4.22)
(4.22)
or
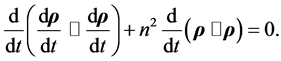 (4.23)
(4.23)
Substituting from the first of Equations (4.10) this becomes
 (4.24)
(4.24)
or, by Equations (2.2) and (2.3),
 (4.25)
(4.25)
From Equation (4.19) we see that the two terms in this equation equal the respective kinetic and potential energies of a unit point-mass in the shell.
For a point-mass in the core the equation of movement referred to external fixed axes is
 (4.26)
(4.26)
and taking the scalar product of this equation with  we obtain
we obtain
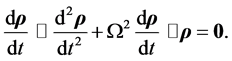 (4.27)
(4.27)
Proceeding as above we now have
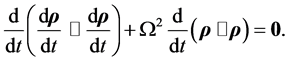 (4.28)
(4.28)
We may define the gravitational potential, V, of a point-mass located in the core as the work to move a unit point-mass from the point concerned to the core-shell boundary to which, by Equation (4.19), is added the work to take the point-mass from the core boundary to infinity so that
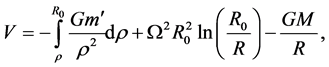 (4.29)
(4.29)
where  in this case, is the mass in the core contained within the radius
in this case, is the mass in the core contained within the radius 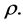 By Equation (3.5) we therefore obtain
By Equation (3.5) we therefore obtain
 (4.30)
(4.30)
and
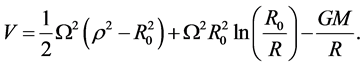 (4.31)
(4.31)
Once again the second term in Equation (4.28) represents twice the rate of increase of the potential energy of a unit point-mass in the core, while the first term equals twice the rate of increase of the kinetic energy of that point-mass. Equations (4.25) and (4.28) express the conservation of energy, respectively, in the shell and core.
5. Transformation of Axes Theorems
If we refer movements in the shell disk to axes fixed to its inner edge (the core-shell boundary), which rotates with angular velocity  we must replace the total differential operator of Appendix B by
we must replace the total differential operator of Appendix B by 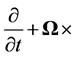 and we then get from Equations (3.9) and (3.10), omitting the term involving changes in
and we then get from Equations (3.9) and (3.10), omitting the term involving changes in 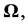
 (5.1)
(5.1)
and Equation (4.20) then leads to the equation of movement in the shell annulus,
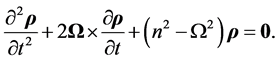 (5.2)
(5.2)
Taking the scalar product of this equation with  we now obtain
we now obtain
 (5.3)
(5.3)
which leads to
 (5.4)
(5.4)
Comparing this equation to Equation (4.23) we see that, in making the transformation from the equation of motion referred to fixed axes to that referred to rotating axes, rotating with angular velocity 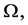 we must subtract a term
we must subtract a term  from the square of velocity in the kinetic energy term at the same time that we replace the operator
from the square of velocity in the kinetic energy term at the same time that we replace the operator 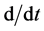 in the equation by
in the equation by  In other words the disk rotation has the effect of modifying the kinetic energy term.
In other words the disk rotation has the effect of modifying the kinetic energy term.
Moreover, from Equations (3.16) and (3.18) it is equally apparent that in calculating the areal velocity, transforming from fixed to rotating axes, we must subtract from h on the right-hand side of the equation the quantity  at the same time that we replace
at the same time that we replace  by
by  (for vectors), when obtaining the transformed equation for areal velocity. The quantity
(for vectors), when obtaining the transformed equation for areal velocity. The quantity 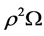 is (twice) the rate at which an arm fixed to the rotating core disk sweeps out area, or may be regarded as the modification in angular momentum due to the use of a rotating reference frame. Note that the areal velocity referred to fixed axes is h/2, and not h.
is (twice) the rate at which an arm fixed to the rotating core disk sweeps out area, or may be regarded as the modification in angular momentum due to the use of a rotating reference frame. Note that the areal velocity referred to fixed axes is h/2, and not h.
On the one hand, from Equations (3.16) and (3.18), (3.21) and (3.22), we arrive at the following theorem which is concerned with the conservation of angular momentum:
Theorem 5.1 In a hypothetical body of mass-points acted upon by gravitation and inertia alone, the mass density of which remains uniform within a central core, the areal velocity, as observed from the rotating core disk which is perpendicular to the axis of rotation, equals the areal velocity, as measured in an external fixed frame of reference, from which is subtracted the quantity 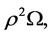 while the operator d/dt, applied to vectors, is changed to
while the operator d/dt, applied to vectors, is changed to 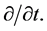
This is the modification to angular momentum due to the use of a rotating reference frame.
On the other hand, from Equations (4.23) and (5.4), regarding the conservation of energy, we have:
Theorem 5.2 In a hypothetical body of mass-points acted upon by gravitation and inertia alone, the mass density of which remains uniform within a central core, the kinetic energy per unit mass, as observed from the rotating core disk, perpendicular to the axis of rotation equals the kinetic energy per unit mass from which must be subtracted the quantity  when the operator d/dt applied to vectors is replaced by
when the operator d/dt applied to vectors is replaced by .
.
6. Discussion and Conclusions
6.1. Spiral Forms
Various proposals have been made in attempts to explain the spirals found on the shell disks of galaxies and, in particular, the density wave theory of Lin and Shu [13] has been thought to account for these features. What has been shown here, however, is the fact that a straight bar of distinguishable material distributed along a diameter across the core and shell annulus will become distorted due to the distribution of angular velocities on the shell annulus. This is given by the first of Equations (4.10). The bar within the shell becomes distorted into a symmetric pair of spirals of Archimedes, as shown by Equations (4.15) and (4.16) (Appendix C), while the portion within the core remains straight and merely rotates. Moreover, if the bar passes through the core center, the bar within the shell annulus becomes distorted into a symmetric pair of spirals of Archimedes.
Shown in Figure 4 are the two prominent dark lanes in M 51 (NGC 5194) and in Table 1 are presented measurements from the image of the polar angle and radius normalized in terms of the radius, 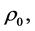 at which the dark lanes become tangled and less distinct along the two arms. In Figure 5 these points have been superposed on one of the Archimedean spirals described by
at which the dark lanes become tangled and less distinct along the two arms. In Figure 5 these points have been superposed on one of the Archimedean spirals described by 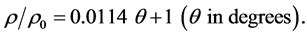
Many spiral galaxies [14] are barred spirals and the boundary of the shell domain in these cases is easily

Figure 4. Image of the two prominent dark lanes in M51 (NGC 5194) (NASA).

Table 1. Polar coordinates of points in the two principal dark lanes of M 51.
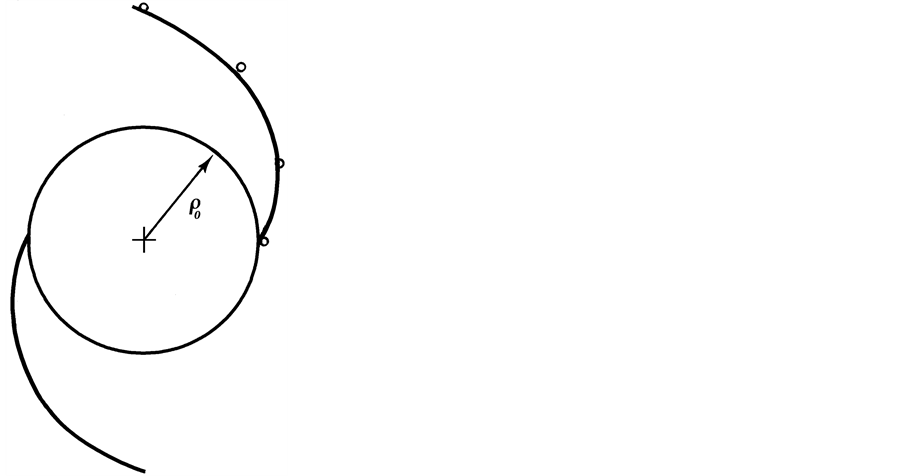
Figure 5. Points from the two prominent dark lanes (mirror imaged) in M51 (NGC 5194) superimposed on the Archimedean spiral .
.
found on the basis of the theory above. Only in the case of spiral galaxies such as F 568-3 and UGC 4325, however, does the inner shell boundary correspond to the core boundary.
The second term on the left-hand side of Equation (3.12) represents the familiar Coriolis force per unit mass. This force acts at right-angles to the arm joining the point-mass to O in Figure 3 and under steady rotation replaces the gravitational force. It is simple to show, however, from equations such as (3.6) or (3.8), (4.20) or (4.21) that spirals cannot represent mass trajectories. In fact, near the edge of the shell annulus, to obtain a trajectory in the form of a spiral of Archimedes Newton’s law of gravitation would have to be replaced by a law in which the force acting on a point-mass varies as the inverse cube of radial distance from the centre of the core.
6.2. Mass Density in the Core
The core rotates with angular velocity 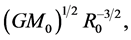 where
where 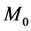 is the total mass of the galactic core and
is the total mass of the galactic core and
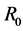 is its effective radius. For F586-3
is its effective radius. For F586-3  equals almost 14 seconds of arc or 1.23 × 1017 m [1] and from the above expression we obtain for the period of the core 7.73 × 1012 s or 0.25 × 106 Years. The core rotates much more rapidly than the outer shell. By Equation (2.3) and the above period, taking G equal to 6.67 × 10−11 Nm2∙Kg−2 and a solar mass [15] equal to 1.9891 × 1030 Kg we get a value of 1.8 × 1037 Kg or 9.3 × 106 solar masses for the galactic core of F 586-3. From the values above we then obtain for the mass density in the core of F 586-3 the value 2.31 × 10−15 Kg∙m−3. No hypothesis has been advanced concerning the constancy of mass density in the cores of spiral galaxies such as F568-3 and UGC 4325 but the figure above may have some significance in this regard.
equals almost 14 seconds of arc or 1.23 × 1017 m [1] and from the above expression we obtain for the period of the core 7.73 × 1012 s or 0.25 × 106 Years. The core rotates much more rapidly than the outer shell. By Equation (2.3) and the above period, taking G equal to 6.67 × 10−11 Nm2∙Kg−2 and a solar mass [15] equal to 1.9891 × 1030 Kg we get a value of 1.8 × 1037 Kg or 9.3 × 106 solar masses for the galactic core of F 586-3. From the values above we then obtain for the mass density in the core of F 586-3 the value 2.31 × 10−15 Kg∙m−3. No hypothesis has been advanced concerning the constancy of mass density in the cores of spiral galaxies such as F568-3 and UGC 4325 but the figure above may have some significance in this regard.
Equation (4.12) gives the entire mass of the galaxy. From our formulae the mass of F568-3 is equal to 1.46 × 1020 R Kg, where R is the effective outer radius in meters. Spiral galaxies are thought to have masses that lie in the range 109 - 1012 solar masses or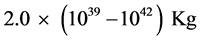 . Therefore, for F 568-3, a value of the outer radius of at least 1.4 × 1019 m seems to be required.
. Therefore, for F 568-3, a value of the outer radius of at least 1.4 × 1019 m seems to be required.
6.3. Conclusions
A stylized version of a galaxy of the same type as F 568-3 or UGC 4325 has been investigated analytically and, on the basis of the hypothesis that the mass densities in the cores of such galaxies remain uniform, the following principles have been established.
1. Four new and inter-connected theorems of Astrodynamics, which will be useful in further investigations, have been proven.
2. The central plane, C (Figure 2 and Figure 3), of the core domain rotates in the same fashion as a phonograph turn-table.
3. In the shell, the mass density of coldand hot-matter varies as the inverse square of radial distance (Equation (4.9), while the angular velocity remains inversely proportional to radial distance from the axis of rotation (first of Equation (4.10). Observations have been made on a number of spiral galaxies in exact agreement with the second of these conclusions, which therefore supports all of the principles that follow from it as well as the fundamental Hypothesis 2.1.
4. Spirals in spiral galaxies begin as straight bar shaped features extending across the shell annuli and core disks. Due to the (see 3 above) variations in angular velocity on the cores and shell disks, the bars become distorted into a pair of symmetrically disposed spirals of Archimedes outside of the core remaining undisturbed, apart from a rigid body rotation, within the core (Equations (4.15) and (4.16)).
These results, the precision of their agreement with recent high quality observations, and the simple hypothesis that supports them demand an explanation of the constancy of mass density in the cores of spiral galaxies and the significance of the results above is that it they simply forbid the existence of so called black-holes in the cores of spiral galaxies.
Acknowledgements
The author would like to express his sincere thanks to the reviewer, who has furnished some very helpful suggestions leading to improvements in the presentation of this paper and the patience of the typesetters in coping with fine adjustments to the mathematical notation.
Appendix A
Figure 6 shows a section through a spherical shell of constant thickness and uniform mass density. In order to determine the gravitational force exerted by the shell at an interior point, such as O, we construct a double cone through O and the section in Figure 6 contains the axis of the double cone and the centre of the sphere.
Let 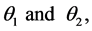 with respective complementary angles
with respective complementary angles  equal the angles in which circles with centres at O and radii
equal the angles in which circles with centres at O and radii 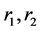 intersect the inner surface of the shell. If
intersect the inner surface of the shell. If 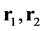 are the radius vectors from O to the respective surface elements
are the radius vectors from O to the respective surface elements  on the shell, we obtain for the forces acting on a point-mass, m, at O due to the two surface elements
on the shell, we obtain for the forces acting on a point-mass, m, at O due to the two surface elements
 (A.1)
(A.1)
From the formula
 (A.2)
(A.2)
for the solid angle, 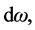 subtended at O by a shell element of area,
subtended at O by a shell element of area, 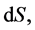 with unit normal outward drawn vector, n, we get
with unit normal outward drawn vector, n, we get
 (A.3)
(A.3)
where  is the mass per unit area on the shell. By a well known theorem concerned with the geometry of circles we have
is the mass per unit area on the shell. By a well known theorem concerned with the geometry of circles we have  and because the triangles
and because the triangles  and
and 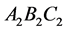 are right-angled triangles it follows that
are right-angled triangles it follows that 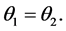 Therefore from Equation (A.3) we obtain
Therefore from Equation (A.3) we obtain
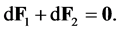 (A.4)
(A.4)
By considering the entire shell to be intersected by cones, such as those above, and summing we see that the shell exerts zero force on a point-mass located at an interior point. Clearly the shell does not have to be thin, as many thin shells may be nested together to form a thick-walled shell to which the theorem above still applies.
If the point O lies outside the shell a very different result is obtained, due to the properties of solid angle. In this case the force on m is directed towards the shell centre and equals  where M is the mass of the shell and r is the radial distance of O from its centre.
where M is the mass of the shell and r is the radial distance of O from its centre.

Figure 6. Gravitational forces acting inside a shell of uniform thickness and density, due to two elements of area where the shell has been intersected by a double cone through the point O.
Appendix B: Axes Embedded in a Rotating Body
B.1. The Euler Formula
Let (t, n, b) (Figure 3) be a right-handed set of mutually orthogonal unit vectors directed along the respective (t, n, b) coordinate lines (not necessarily cartesian). Then we require for the continued perpendicularity and length invariance of these unit vectors
 (B.1)
(B.1)
By differentiating these equations with respect to the time t (italics distinguish the symbol for the time from the unit vector t, which is presented in boldface text) we obtain
 (B.2)
(B.2)
and these equations are satisfied by
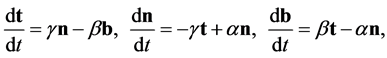 (B.3)
(B.3)
where 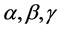 are constants. Denoting the vector product of two vectors [8] by the symbol
are constants. Denoting the vector product of two vectors [8] by the symbol 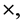 we can show, from these equations, that
we can show, from these equations, that
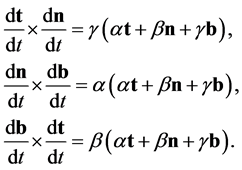 (B.4)
(B.4)
Because the vector products above lie in the same plane, since  and even
and even 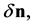 if n changes, must lie on a plane normal to the angular velocity vector,
if n changes, must lie on a plane normal to the angular velocity vector,  , it follows that
, it follows that
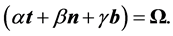
We have therefore shown that
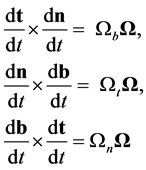 (B.5)
(B.5)
and from Equation (B.3) we now have
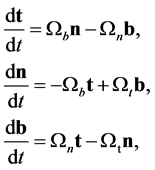 (B.6)
(B.6)
or
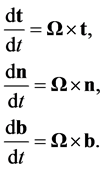 (B.7)
(B.7)
These equations describe the rates of change of the unit vectors fixed with respect to a turn-table rotating with angular velocity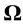 , as observed from an external fixed reference frame. If A is any vector, whatsoever, having constant components when referred to the above axes embedded within the rotating frame, it follows from Equations (B.7) that
, as observed from an external fixed reference frame. If A is any vector, whatsoever, having constant components when referred to the above axes embedded within the rotating frame, it follows from Equations (B.7) that
 (B.8)
(B.8)
B.2. Total Rate of Change
Changes can also occur within the rotating frame. To denote this remaining component of the vectorial rate of change with respect to the time, as observed from within the rotating reference frame and due to change with respect to the embedded (t, n, b) axes (as if they were fixed), we utilize the symbol for partial differentiation,  (the unit vector t is presented in bold-face text so that there is no confusion with the symbol for time). The symbol
(the unit vector t is presented in bold-face text so that there is no confusion with the symbol for time). The symbol  only has operational meaning when applied to a vector. When applied to a scalar it must be replaced by
only has operational meaning when applied to a vector. When applied to a scalar it must be replaced by 
When 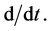 is applied, as an operator, to a vector it gives the total rate of change, due to rotation of the axes, as above, together with changes relative to those axes. By superposition we then have, for the total rate of change of any vector A due to changes with respect to the axes embedded in the rotating frame as well as due to forces engendered by the rotation itself,
is applied, as an operator, to a vector it gives the total rate of change, due to rotation of the axes, as above, together with changes relative to those axes. By superposition we then have, for the total rate of change of any vector A due to changes with respect to the axes embedded in the rotating frame as well as due to forces engendered by the rotation itself,
 (B.9)
(B.9)
where  now denotes the total rate of change with the time as observed from an external fixed frame of reference. We note that by Equation (B.9)
now denotes the total rate of change with the time as observed from an external fixed frame of reference. We note that by Equation (B.9)
 (B.10)
(B.10)
Appendix C: Spirals in Spiral Galaxies
Several cardboard or paper disks are cut with a range of diameters. These are then mounted concentrically on a pin which is fastened to a board. A diameter, D, is drawn in pencil across the set of disks. Then, by one of any number of methods, a given fixed length, L, is marked, again in pencil, along the circumference of each disk, commencing from the diameter, D. Each disk is then turned in the same sense until the marks representing the length, L, are brought to positions on a straight-edge set up to coincide with D. The portions of D originally collinear with the pin will then be seen to form a pair of symmetrically disposed spirals of Archimedes. Inside the innermost circle the portion of D is, of course, unaltered in shape.