Eigenstructure Assignment Method and Its Applications to the Constrained Problem ()
1. Introduction
Eigenstructure assignment method plays a capital role in control theory of linear systems. The state feedback control law is used in this end, leading to change eigenvalues or eigenvectors of the open loop to desired ones in the closed loop. This method is usually realized in order to perform optimal or stabilizing control laws ([1] -[9] ). These articles and the references therein constitute a comprehensive summary and an important bibliography on the control of linear systems with input saturation. Indeed, authors have used different concepts leading to many methods for eigenstructure assignment control laws to regulate linear systems with input saturation.
Throughout this paper, we will be interested in continuous time systems of the form
 (1)
(1)
The matrices A and B are real and constant:  and
and  with
with . The vector
. The vector  represents the state vector of the system and
represents the state vector of the system and  is the control vector. We suppose that the spectrum of the matrix A contains
is the control vector. We suppose that the spectrum of the matrix A contains  desirable or stable eigenvalues
desirable or stable eigenvalues  and
and  undesirable or unstable eigenvalues
undesirable or unstable eigenvalues . We also suppose that the pair
. We also suppose that the pair  is stabilizable.
is stabilizable.
Presence of undesirable eigenvalues makes System (1) unstable and, in [4] or in [10] , methods to overcome the instability of System (1), keeping unchanged the open-loop stable eigenvalues and the corresponding eigenspace  and replacing the remaining undesirable eigenvalues by other chosen values, were given. But, in these methods, additional conditions on System (1) should be satisfied.
and replacing the remaining undesirable eigenvalues by other chosen values, were given. But, in these methods, additional conditions on System (1) should be satisfied.
In this paper, we try to get rid of these additional conditions on System (1). First, we should give some outlines on the methods described in [4] or in [10] . In [4] , the method, called the inverse procedure, consists of giving a matrix  with some desirable or stable spectrum and then computing, when possible, a full rank feedback matrix
with some desirable or stable spectrum and then computing, when possible, a full rank feedback matrix  such that:
such that:
 (2)
(2)
and the kernel of  is the stable subspace. In this case, the spectrum of the matrix
is the stable subspace. In this case, the spectrum of the matrix  is stable since it is constituted by the desirable eigenvalues of A and the chosen spectrum of H. In other words, the eigenvalues of H will replace, in the closed-loop, the undesirable eigenvalues of A. With the change of variables
is stable since it is constituted by the desirable eigenvalues of A and the chosen spectrum of H. In other words, the eigenvalues of H will replace, in the closed-loop, the undesirable eigenvalues of A. With the change of variables  in the initial system, we get
in the initial system, we get
 (3)
(3)
which allows one to focus on the unstable part of this system.
The inverse procedure described in [4] ensures the existence of a matrix F that satisfies the conditions mentioned above and gives a way to compute it under the following conditions:
• The matrix H is diagonalizable; that is, there exist linearly independent eigenvectors  of H associated to some stable eigenvalues
of H associated to some stable eigenvalues .
.
• The endomorphism induced by the matrix A on the stable subspace is diagonalizable; that is, there exist linearly independent eigenvectors  of A in the subspace
of A in the subspace .
.
• The spectrum of A and the spectrum of H are disjoint.
• The matrix

is invertible.
Under these conditions and according to the method described in [4] , the matrix  is unique and is given by
is unique and is given by
 (4)
(4)
where  is the null vector of
is the null vector of .
.
In [10] , the condition b) is kept and a new assumption should be fulfilled:
1. the matrix  is invertible.
is invertible.
The method described in [10] consists of computing a matrix  such that its rows span the orthogonal of the stable subspace by taking, for example the first
such that its rows span the orthogonal of the stable subspace by taking, for example the first  rows of
rows of  and then, for a stable matrix
and then, for a stable matrix . Then, according to the method described in [10] , the feedback matrix
. Then, according to the method described in [10] , the feedback matrix  is given by
is given by  where
where  is the inverse matrix of the solution of the Sylvester equation
is the inverse matrix of the solution of the Sylvester equation
 (5)
(5)
and  is a matrix such that
is a matrix such that .
.
In this paper, we generalize the method described in [10] to a more general class of systems for which the condition d’) is not necessary. In fact, no additional condition is needed to deal with System (1). As in [10] , the feedback matrix F is always given by KV where K is an invertible matrix of  such that
such that  is the solution of the Sylvester Equation (5).
is the solution of the Sylvester Equation (5).
The methods described in [10] or in [4] are, in fact, partial pole placement methods in which the desirable eigenvalues of the matrix A are kept in the closed-loop. But, it may happen that these desirable eigenvalues are close to the imaginary axis which causes a slow convergence rate to the origin. To overcome this problem, a total pole placement is needed. The technique of augmentation (see [5] and [6] ) allows one to perform a total pole placement when the matrix B needs not be of full rank. This is possible with the inverse procedure [4] , but not with the method described in [10] since, under the condition 1, the matrix B is of full rank.
So, from one hand, the method that we present constitutes a generalization of the two methods described in [10] or in [4] without any other additional condition on the systems and, from another hand, allows one to make, if necessary, a total pole placement by the use of the augmentation technique.
The paper is organized as follows: In Section 1, definitions, notations and some known facts are presented to be used in the sequel. The main results are presented in Section 2 together with an illustrative example. Some particular cases are presented in Section 3. Section 4 is devoted to the total eigenstructure problem with the illustrative example of the double integrator.
2. Preliminaries
• 2.1. Notations and Definitions
•  is the identity matrix of
is the identity matrix of  for
for .
.
• Matrices of the form  are called scalar matrices for
are called scalar matrices for  and
and .
.
• If  is a
is a  real matrix, for some
real matrix, for some , its transpose, the
, its transpose, the  real matrix, will be denoted by
real matrix, will be denoted by .
.
• When we view  as an euclidean space, the usual inner product
as an euclidean space, the usual inner product  is considered, that is,
is considered, that is,

where  and
and  are two vectors of
are two vectors of .
.
• If  is a nonempty subset of
is a nonempty subset of , its orthogonal will be denoted by
, its orthogonal will be denoted by , that is•
, that is• 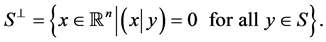
• For a real number , we define
, we define
• 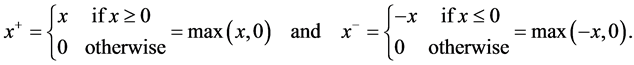
• If  is a
is a  real matrix, for some
real matrix, for some ,
,  will denote the coefficient of
will denote the coefficient of  corresponding to the
corresponding to the  row-column.
row-column.
• If  is a
is a  real matrix, for some
real matrix, for some ,
,  is the
is the  real matrix defined by
real matrix defined by

where  and
and 
• For real matrices (or real vectors)  and
and , we say that
, we say that  is less than or equal to
is less than or equal to  if every component of
if every component of  is less than or equal to the corresponding component of
is less than or equal to the corresponding component of . We then write
. We then write .
.
• If  is a
is a  real matrix, for some
real matrix, for some ,
,
(a)  is the kernel of
is the kernel of : the subspace of
: the subspace of  of vectors
of vectors  such that
such that .
.
(b)  is the image of
is the image of : the subspace of
: the subspace of  spanned by the columns of
spanned by the columns of  and also the set of vectors of the form
and also the set of vectors of the form  with
with .
.
• If  is a
is a  real matrix, for some
real matrix, for some ,
,  denotes its spectrum in the field of complex numbers
denotes its spectrum in the field of complex numbers .
.
• If  is a complex number then
is a complex number then  is the real part of
is the real part of .
.
2.2. Some Notes on the Stable-Unstable Subspaces
1. To System (1), we associate:
(a) The two polynomials
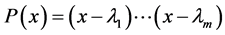
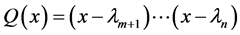
that are factors of the characteristic polynomial of .
.
In case of , polynomial Q is just the constant polynomial 1.
, polynomial Q is just the constant polynomial 1.
(b) The two subspaces of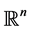 ;
;  and
and .
.
In case of , the subspace
, the subspace  is just the trivial subspace
is just the trivial subspace .
.
Remark 1
1. Since 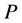 and
and  are coprime,
are coprime,  and
and  are complementary subspaces of
are complementary subspaces of . Moreover, we have
. Moreover, we have

and also
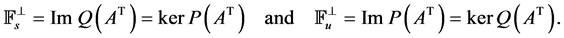
2. Since pair  is stabilizable, we have
is stabilizable, we have
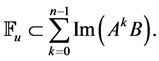
2.3. Some Notes on Sylvester Equation
Many problems in analysis and control theory can be solved using the well known of Sylvester equation. This equation is widely studied or used in the literature ([10] -[15] ). Since Sylvester equation plays a central role in the development of this work, we shall recall conditions under which it has a unique solution. A Sylvester equation is any equation of the form
 (6)
(6)
where M is a  real or complex matrix, N is a
real or complex matrix, N is a  real or complex matrix and C is a
real or complex matrix and C is a  real or complex matrix while matrix X stands for an unknown
real or complex matrix while matrix X stands for an unknown  real or complex matrix. The following well known result gives a sufficient condition for the existence and uniqueness of a solution of Sylvester Equation (6).
real or complex matrix. The following well known result gives a sufficient condition for the existence and uniqueness of a solution of Sylvester Equation (6).
Theorem 1
If spectrums of matrices M and N are disjoint,  , then Sylvester Equation (6) has a unique solution.
, then Sylvester Equation (6) has a unique solution.
2.4. System (1) with Constraints on the Control
Consider System (1) with the assumption that the control  is constrained to be in the region
is constrained to be in the region  of
of  defined by
defined by
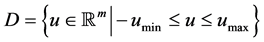
where  and
and  are positive vectors in
are positive vectors in . Note that the region
. Note that the region  is a non symmetrical polyhedral set as is generally the case in practical situations. Let us first consider the unconstrained case where the regulator problem for System (1) consists in realizing a feedback law as
is a non symmetrical polyhedral set as is generally the case in practical situations. Let us first consider the unconstrained case where the regulator problem for System (1) consists in realizing a feedback law as
 (7)
(7)
where  is chosen in
is chosen in  with full rank
with full rank . In this case, System (1) becomes
. In this case, System (1) becomes
 (8)
(8)
The stability of the closed loop System (8) is obtained if, and only if,
 (9)
(9)
for all eigenvalues  of the matrix
of the matrix . In the constrained case, the approach proposed in ([4] -[6] ) consists of giving conditions allowing the choice of a stabilizing controller (7) in such a way that the state is constrained to evolve in a specified region of
. In the constrained case, the approach proposed in ([4] -[6] ) consists of giving conditions allowing the choice of a stabilizing controller (7) in such a way that the state is constrained to evolve in a specified region of  defined by
defined by
 (10)
(10)
Note that the domain  is bounded only in case of
is bounded only in case of . In fact, when
. In fact, when , the subspace
, the subspace  has dimension
has dimension  and is a subset of this domain. Suppose now that there is a matrix
and is a subset of this domain. Suppose now that there is a matrix  such that
such that
 (11)
(11)
Hence, by letting , we get
, we get
 (12)
(12)
and then . We would get
. We would get  for all
for all  whenever
whenever . We say that D is positively invariant with respect to the motion of System (12). More generally, we give the following definition of positive invariance.
. We say that D is positively invariant with respect to the motion of System (12). More generally, we give the following definition of positive invariance.
Definition 1
A nonempty subset  of
of  is said to be positively invariant with respect to the motion of System (12) if, for every initial state
is said to be positively invariant with respect to the motion of System (12) if, for every initial state  in
in , the motion
, the motion  remains in
remains in  for every
for every .
.
The following theorem gives necessary and sufficient conditions for domain D to be positively invariant with respect to the motion of System (12).
Theorem 2 ([6])
The domain D is positively invariant with respect to the motion of System (12) if, and only if,
 (13)
(13)
where  is the real vector
is the real vector 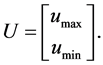
Till now, we have supposed the existence of a matrix H that satisfies Equation (11). The following result, which does not take into account the constrained problem, gives necessary and sufficient conditions for its existence.
Theorem 3 ([4])
 is positively invariant with respect to the motion of System (12) if, and only if, there is a matrix
is positively invariant with respect to the motion of System (12) if, and only if, there is a matrix  such that Equation (11) is satisfied.
such that Equation (11) is satisfied.
Note that  is positively invariant with respect to the motion of System (12) is the same as
is positively invariant with respect to the motion of System (12) is the same as  is stable by matrix A. If the constrained problem is taken into account, the following theorem gives necessary and sufficient conditions for positive invariance of the domain of states
is stable by matrix A. If the constrained problem is taken into account, the following theorem gives necessary and sufficient conditions for positive invariance of the domain of states .
.
Theorem 4 ([6])
The domain  is positively invariant with respect to System (8) if, and only if, there is a matrix
is positively invariant with respect to System (8) if, and only if, there is a matrix  such that Equation (11) is satisfied and
such that Equation (11) is satisfied and
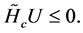
3. Main Results
At first, we compute, and fix in the sequel, some matrix  such that its rows span the subspace
such that its rows span the subspace . Since the dimension of the subspace
. Since the dimension of the subspace  is
is , the matrix
, the matrix  is of full rank
is of full rank .
.
Proposition 1 There is a unique matrix  such that
such that . This matrix is given by
. This matrix is given by
 (14)
(14)
and its spectrum is .
.
wang#title3_4:spwang#title3_4:spProof.
Let  be the endomorphism of
be the endomorphism of  canonically associated to matrix
canonically associated to matrix , that is,
, that is,
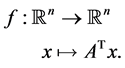
The subspace  is stable under f (that is, f(x) belongs to
is stable under f (that is, f(x) belongs to  whenever x is in
whenever x is in ). So, one can define the endomorphism g induced by f on
). So, one can define the endomorphism g induced by f on . Matrix
. Matrix , when identified with its column vectors, can be seen as a basis of
, when identified with its column vectors, can be seen as a basis of . In this basis, if we denote by L the matrix of g, we will have
. In this basis, if we denote by L the matrix of g, we will have
 (15)
(15)
Let now . By transposition of formula (15), we get
. By transposition of formula (15), we get . Since g is induced by f on
. Since g is induced by f on , its spectrum is
, its spectrum is  which is also the spectrum of Λ. Formula (14) derives from the fact that V is of full rank m and shows the uniqueness of the matrix Λ. ,
which is also the spectrum of Λ. Formula (14) derives from the fact that V is of full rank m and shows the uniqueness of the matrix Λ. ,
Proposition 2
For any matrix  such that
such that , there is an invertible matrix
, there is an invertible matrix  such that
such that  and
and  is of full rank
is of full rank .
.
Proof.
Let 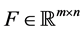 such that
such that . Since dimension of
. Since dimension of  is n − m, rank formula shows that F is of full rank m. Let now
is n − m, rank formula shows that F is of full rank m. Let now  such that
such that . Then,
. Then,  and then
and then . But matrix
. But matrix
 is invertible, so U = 0 and this shows that matrix
is invertible, so U = 0 and this shows that matrix  is invertible. Clearly,
is invertible. Clearly,  is invertible. For
is invertible. For , we have
, we have

Since , we have
, we have  and then
and then
 . So
. So
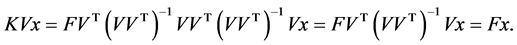
Since this equality holds for all , we have
, we have . Theorem 5 Let
. Theorem 5 Let  be a set of complex numbers stable under complex conjugation such that
be a set of complex numbers stable under complex conjugation such that  and
and  with spectrum
with spectrum . Then, there is matrix
. Then, there is matrix  of full rank
of full rank  such that
such that  and
and  if, and only if, Sylvester equation
if, and only if, Sylvester equation
 (16)
(16)
has a unique invertible solution  such that
such that .
.
wang#title3_4:spwang#title3_4:spProof.
The if part: Let  be of full rank matrix such that
be of full rank matrix such that  and
and . From Proposition 2, there is an invertible matrix
. From Proposition 2, there is an invertible matrix  such that F = KV. Since VA = ΛV , we get
such that F = KV. Since VA = ΛV , we get
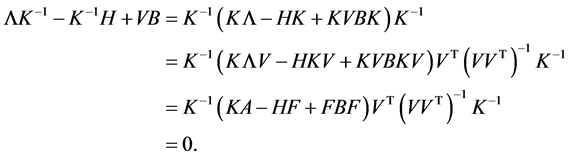
Then  is an invertible solution to Sylvester Equation (16).
is an invertible solution to Sylvester Equation (16).
The only if part: Suppose now that Sylvester Equation (16) has an invertible solution X and let . Matrix F = KV satisfies
. Matrix F = KV satisfies  because matrix K is invertible and then is of full rank m. We also have
because matrix K is invertible and then is of full rank m. We also have

,
Remark 2
Because we are focusing on the partial assignment problem, eigenvalues of matrix H should be desirable, that is, matrix H should be Hurwitz. The undesirable eigenvalues  of A must all be different from those of H. So, assumption
of A must all be different from those of H. So, assumption  in Theorem 5 above is necessary.
in Theorem 5 above is necessary.
Example 1 Consider the linear time-invariant multivariable system described by

with
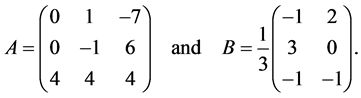
The control vector is submitted to the constraint  such that,
such that,

Eigenvalues of A are  and
and  and pair
and pair  is stabilizable. We get first the matrix
is stabilizable. We get first the matrix
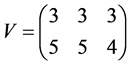
Note that the rows of V are orthogonal to the eigenvector of A associated to the stable eigenvalue  of A. We, then, choose the matrix
of A. We, then, choose the matrix
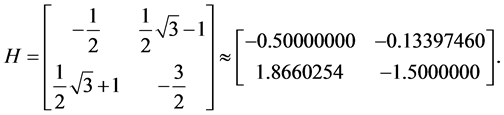
This matrix is not diagonalizable and its eigenvalues are . Besides, inequality (13) is satisfied. We use the formula
. Besides, inequality (13) is satisfied. We use the formula  to get
to get
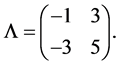
Then, we solve the equation (15) and use the inverse of its solution to get the feedback matrix
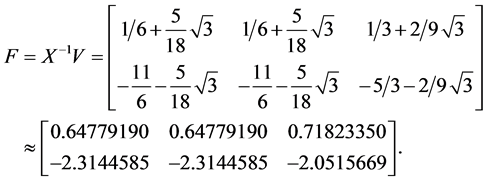
Finally,  is the unique eigenvalue of the matrix
is the unique eigenvalue of the matrix .
.
Figure 1 shows that, starting from two different and admissible controls, the corresponding trajectories, in the control space, converge to the origin without saturations.
3. Particular Cases
3.1. Case of Single Input Linear Systems
We discuss the particular case of single input linear systems, that is, when . As described in the general case, we start by computing matrix V which is in case of
. As described in the general case, we start by computing matrix V which is in case of  a row vector that is orthogonal to
a row vector that is orthogonal to  and is easy to get. Matrix
and is easy to get. Matrix  is only the real
is only the real ; the unique undesirable eigenvalue of
; the unique undesirable eigenvalue of . If we choose H to be a
. If we choose H to be a
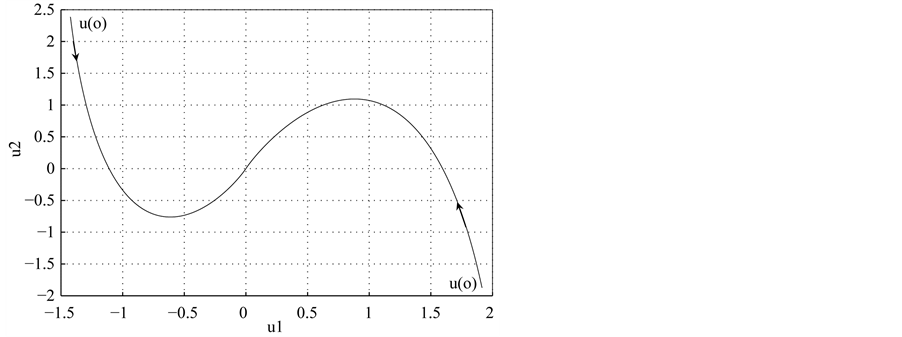
Figure 1. Trajectories of the system  from two different initial controls in
from two different initial controls in .
.
negative real number, Theorem 5 ensures that all matrices F (row vectors) are of the form KV where  is a nonzero real solution to the simple “Sylvester equation”
is a nonzero real solution to the simple “Sylvester equation”
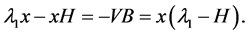
This equation has a nonzero solution if, and only if, the real number  is nonzero. That is,
is nonzero. That is,
 (17)
(17)
Formula  shows that
shows that  is a left eigenvector of
is a left eigenvector of  associated to the undesirable eigenvalue
associated to the undesirable eigenvalue  and then
and then  for every
for every . But pair
. But pair  is stabilizable, so
is stabilizable, so
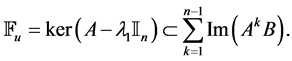
If we suppose that , then we should have
, then we should have
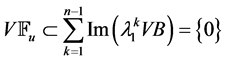
and then . We also have
. We also have  and
and . This shows that
. This shows that  which is not true.
which is not true.
As a consequence, we have the following result.
Proposition 3 For a given left eigenvector  of
of  associated to the unique eigenvalue
associated to the unique eigenvalue  and for a negative real number
and for a negative real number , we have
, we have  and matrix
and matrix  given by
given by
 (18)
(18)
The spectrum of  is then
is then .
.
3.2. Case Where the Matrix VB Is Nonsingular
We have seen in the last paragraph that, when , a necessary and sufficient condition for Sylvester Equation (15) to have nonsingular solution (nonzero real number in fact) is that the real
, a necessary and sufficient condition for Sylvester Equation (15) to have nonsingular solution (nonzero real number in fact) is that the real  is nonzero. We also have seen that this last condition;
is nonzero. We also have seen that this last condition; , is equivalent to the fact that pair
, is equivalent to the fact that pair  is stabilizable. In case of
is stabilizable. In case of , it may happen that pair
, it may happen that pair  is stabilizable but matrix
is stabilizable but matrix  is singular as will show the following example.
is singular as will show the following example.
Example 2
Consider System (1) with
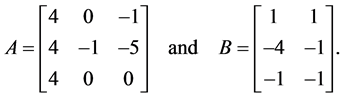
Eigenvalues of A are  and
and . The last desirable eigenvalue
. The last desirable eigenvalue  is associated to the eigenvector
is associated to the eigenvector  of
of  that spans the subspace
that spans the subspace . Matrix V is then
. Matrix V is then

Matrix  is singular since it is
is singular since it is
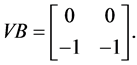
Controllability matrix is given by

and is of full rank 3. This shows that pair  is stabilizable since it is even controllable.
is stabilizable since it is even controllable.
The case of matrix  is nonsingular can be seen as a general case of
is nonsingular can be seen as a general case of  when
when . So, it deserves a special study that will be the aim in the sequel of this paragraph. In the following theorem, we give a necessary and sufficient condition for matrix
. So, it deserves a special study that will be the aim in the sequel of this paragraph. In the following theorem, we give a necessary and sufficient condition for matrix  to be nonsingular.
to be nonsingular.
Theorem 6
Matrix  is nonsingular if, and only if,
is nonsingular if, and only if,  and
and  are complementary subspaces of
are complementary subspaces of ; that is,
; that is, .
.
Proof.
The if part: Since VB is nonsingular, matrix B is of full rank m. To complete the proof of the if part, we shall show that  since the dimension of the subspace
since the dimension of the subspace  is n − m. Recall that VX = 0 for any vector X in
is n − m. Recall that VX = 0 for any vector X in . If now X is both in
. If now X is both in  and Im(B), then there is
and Im(B), then there is  such that X = BU and then
such that X = BU and then
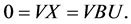
This shows that U = 0 since VB is nonsingular and, then, X = 0.
The only if part: From the fact that VX = 0 for any vector X in ; that is
; that is , V is of full rank m; that is
, V is of full rank m; that is . Moreover, from the fact that
. Moreover, from the fact that , we get
, we get
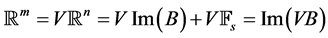
since V is linear. This shows that the rank of VB is m and that it is nonsingular. The following theorem gives another method to get a partial pole assignment under the assumption that  is nonsingular.
is nonsingular.
Theorem 7
Suppose that matrix  is nonsingular and let matrix
is nonsingular and let matrix  be such that
be such that
 ,
,  and
and  is nonsingular. Then,
is nonsingular. Then,
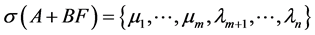
where .
.
wang#title3_4:spwang#title3_4:spProof.
Let  and
and . Then,
. Then,

This shows that  is a nonsingular solution to Sylvester Equation (16) and, by Theorem 5, that matrix
is a nonsingular solution to Sylvester Equation (16) and, by Theorem 5, that matrix  satisfies
satisfies
 ,
,
Example 3
Consider System (1) with
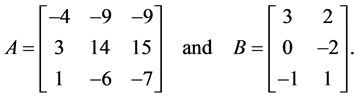
Eigenvalues of A are  and
and . The last desirable eigenvalue
. The last desirable eigenvalue  is associated to the eigenvector
is associated to the eigenvector  of
of  that spans the subspace
that spans the subspace . Matrix
. Matrix  is then
is then
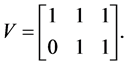
Matrix  is nonsingular and matrix
is nonsingular and matrix  is given by
is given by
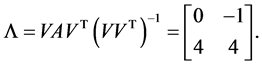
Now choose  that are the eigenvalues of the matrix
that are the eigenvalues of the matrix . Then,
. Then,

4. A Total Eigenstructure Problem
Note that, when m and n are equal, matrix V described in the last section is now any invertible matrix of . That is why, we suppose
. That is why, we suppose . Then matrix
. Then matrix  is simply
is simply  and Sylvester Equation (15) becomes
and Sylvester Equation (15) becomes
 (19)
(19)
where H is a real  matrix with desirable spectrum. So, if the unique solution X of Equation (20) is invertible, then the spectrum of
matrix with desirable spectrum. So, if the unique solution X of Equation (20) is invertible, then the spectrum of  and the one of H are equal, where matrix F is
and the one of H are equal, where matrix F is . Suppose now that
. Suppose now that . The technique of augmentation (see [5] and [6] ) consists of augmenting the matrix
. The technique of augmentation (see [5] and [6] ) consists of augmenting the matrix  by adding zeros in order to get a new matrix
by adding zeros in order to get a new matrix . One should also complete the control vector
. One should also complete the control vector  by fictive real numbers to get
by fictive real numbers to get . We also replace the assumption: “the pair
. We also replace the assumption: “the pair  is stabilizable” by “the pair
is stabilizable” by “the pair  is controllable.” System (1) which becomes
is controllable.” System (1) which becomes
 (20)
(20)
does not change. The matrix  is now a real
is now a real  matrix with some desirable spectrum
matrix with some desirable spectrum  which does not contain any eigenvalue of matrix
which does not contain any eigenvalue of matrix . If the unique solution
. If the unique solution  of Sylvester equation
of Sylvester equation
 (21)
(21)
is invertible, we let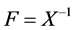 . The matrices
. The matrices  and
and  have the same spectrum
have the same spectrum . If
. If  is the matrix of the first
is the matrix of the first  rows of
rows of , then
, then  assigns the spectrum of
assigns the spectrum of 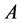 to
to .
.
Example 4
Consider the problem of stabilization of the following double integrator system
 (22)
(22)
with
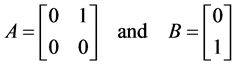
subject to the constraint . The matrix
. The matrix  and the vector
and the vector  are respectively augmented to
are respectively augmented to
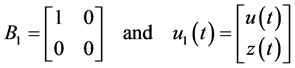
such that  where
where  and
and  are fictive positive real numbers. Let, for example,
are fictive positive real numbers. Let, for example,  and
and  to get the domain
to get the domain  in the Example 1. We choose the matrix
in the Example 1. We choose the matrix
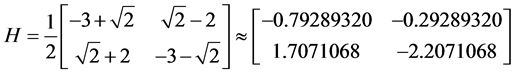
for which the eigenvalues are  and the inequality (13) is satisfied. Then, we solve the Sylvester equation (20) and get
and the inequality (13) is satisfied. Then, we solve the Sylvester equation (20) and get

The feedback matrix , which represents the first row of
, which represents the first row of , is then
, is then
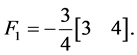
The spectrum of  is then
is then .
.
As in Figure 1 but in the state space, Figure 2 plots two trajectories in the state space starting from two different and admissible initial states and, thanks to the asymptotic stability of the system and the invariance positive property, shows the state convergence to the origin without leaving the domain imposed by the constraints.
5. Conclusion
A method for partial or total eigenstructure assignment problem was presented and examples to illustrate the method were given. The method uses Sylvester equation to find the feedback matrix F when some matrix  is given with a desirable spectrum that will replace all the undesirable eigenvalues of the initial matrix A of System (1) in the closed-loop. This method generalizes the one proposed in [10] without additional conditions on Sys-
is given with a desirable spectrum that will replace all the undesirable eigenvalues of the initial matrix A of System (1) in the closed-loop. This method generalizes the one proposed in [10] without additional conditions on Sys-
tem (5) and allows us to deal with the problem of asymmetrical constraints on the control vector. Examples to show its importance are presented.