1. Introduction
Hydrogenation is a key part of oil refining, and catalyst is the core of hydrogenation. It has been practically proved that the high reactivity and selectivity of a hydrogenation catalyst can be only achieved with the use of presulfurization. So far, the presulfurization of a hydrogenation catalyst is mainly controlled by experience, and thus is unable to realize the optimal and automatic operation or to achieve the catalyst’s optimal activity state. To solve the above problems, accurate and improved theories are needed to guide the practical operations of presulfurization. This set of theories is essentially the presulfurization kinetics laws, which implies the practical significance of presulfurization kinetics.
The kinetics of H2S + H2 mixture in vulcanization of supported or non-supported Co and Mo hydrogenation catalysts was already reported [1] . However, the authors ignored that presulfurization was a nonstationary gassolid uncatalyzed reaction, and did not consider the mass transfer resistance inside catalyst solid grains, which resulted in slight deviation between the models and the real situation [2] [3] . The existing research focuses mainly on the different process conditions when structurally different catalysts are used in presulfurization, but rarely on the kinetics. Based on the research achievements of other gas-solid noncatalytic reaction kinetics [4] -[11] , we aim to improve the presulfurization efficiency of a hydrogenation catalyst and the utilization rate of raw materials. Regarding the optimization of process control and operation, this study provides theoretical basis and potential necessity for investigating the presulfurization kinetics of hydrogenation catalysts. Along with the development of hydrogenation catalysts, studying the presulfurization kinetics laws of catalysts will become a hotspot in research of presulfurization of hydrogenation catalysts. Research of presulfurization of hydrogenation catalysts is significant for promoting the technical advancement in this field and improving the oil refining technology. In this study, the intrinsic kinetics of hydrorefining catalysts in presulfurization was investigated using fixed-bed penetrating method.
2. Experimental
2.1. Materials
The catalysts were paraffin hydrorefining catalysts (active components: WO3—25.00 w%, NiO—7.00 w%). The raw material in sulfurization was a mixture of H2S and H2 (molar ratio 1:3).
2.2. Experimental Installation Flow and Conditions
The experimental installation was divided into two parts: a sulfurization fixed micro-bed and an exhaust gas analyzer. A quartz tube (Φ6 × 1 mm) was chosen to be the fixed micro-bed reactor. Before the experiment, the catalysts were dried by a nitrogen flow at 300˚C for 1 h; then after heating to the reaction temperature, timing was started when the installation was stabilized and gas-exchanged to the sulfurization gas. The exhaust gas after sulfurization was injected via six-way-valve-generated pulses to a thermal conductivity cell for concentration detection. A cold trap was set between the reactor and the thermal conductivity cell to eliminate the effects of water generated during reaction. The spectra were recorded and processed by a chromatography workstation. The gas content variation in the thermal conductivity cell reflected the changes of H2S and H2 together. Since the gas mixture contained more H2, the signals due to H2 content variation were weak. Thus, the area of a peak on the spectrogram mainly reflects the H2S content variation during sulfurization.
After both internal and external diffusions were eliminated, about 0.2 g catalyst was weighed and dense-phase loaded to the middle part of the quartz-tube reactor. The catalyst was filled up-and-down with silica wool, which supported the catalyst and distributed gas. The experimental conditions were showed in Table 1. The temporal changes of H2S concentration from the fixed-bed’s outlet under different reaction conditions were measured at last.
3. Intrinsic Kinetics Model of Presulfurization
3.1. Building and Solving of Mathematical Model
The presulfurization of paraffin hydrorefining catalyst proceeds as follows:
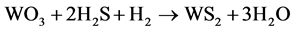 (1)
(1)
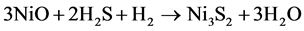 (2)
(2)
For simplification, the solid substrates WO3 and NiO are regarded as a whole, and then the reaction can be changed to:
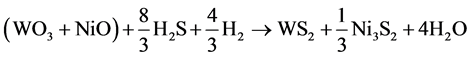 (3)
(3)

Table 1. Experimental conditions of intrintic kinetics.
In the gas mixture for sulfurization, the H2 is largely excessive compared with H2S, and thus the variation of H2 content during reaction could be ignored. Compared with the gas-phase reactants, the concentrations of solid reactants are approximately considered as non-changing or quasi-steady. Based on the unit reaction interface on the catalyst grains and with H2S as the target component, the equation expressing the intrinsic reaction rate of presulfurization is built as follows:
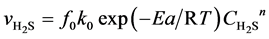 (4)
(4)
Here, 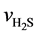 is the reaction rate of H2S, mol·m−2·s; f0 is the correction coefficient that stands for the effect degree of solid diffusion on reaction rate; k0 is the pre-exponential factor, m∙K∙s−2, Ea is the activation energy, kJ·mol−1; T is the reaction temperature, K;
is the reaction rate of H2S, mol·m−2·s; f0 is the correction coefficient that stands for the effect degree of solid diffusion on reaction rate; k0 is the pre-exponential factor, m∙K∙s−2, Ea is the activation energy, kJ·mol−1; T is the reaction temperature, K; 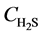 is the concentration of H2S, mol∙m−3; n is the reaction order.
is the concentration of H2S, mol∙m−3; n is the reaction order.
Then f0 and k0 are combined to K then:
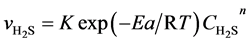 (4’)
(4’)
In this paper, suppose that the active components were homodispersed in the catalyst carrier to form a solid reactant system. The solid reactant grains are spheric, and the temperature difference inside a grain or between the interior and the exterior is ignored. After both internal and external diffusions are eliminated, we consider the effects of solid diffusion in the product layer, and the surface reaction at initial stage is the control step. Based on the above hypotheses and on the unit reaction interface on the catalyst grains, an unreacted shrinking core model is applied to the catalyst solid reactant grains [12] [13] . For a single grain:
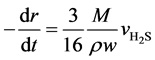 (5)
(5)
Here, r is the radius of the unreacted spherical catalyst, mm; t is the reaction time, s; M is the average molar mass of WO3 and NiO, g∙mol−1; ρ is the catalyst grain density, g∙cm−3; w is the mass fraction of WO3 and NiO in the catalyst.
Without considering interphase resistance, one dimension unhomogeneous model is used to express the beds of the fixed-bed reactor:
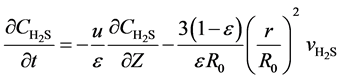 (6)
(6)
Here, u is the gas flow rate, m∙s−1; ε is the bed voidage; Z the bed height, m; R0 is the initial radius of the spherical catalyst, mm.
Integrate Equation (4’) and (6) along the bed, with the following initial and boundary conditions:
At t = 0, at any position on the bed, 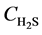 = 0, r = R0;
= 0, r = R0;
At z = 0, at any time, 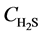 =
= , 0;
, 0;
At z = L, at any time,  =
= .
.
Equations (4) - (6) indicate that the undetermined parameters are activation energy Ea, pre-exponential factor k0, reaction order n, and correction coefficient f0, where 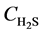 is a function of reaction temperature T, initial H2S concentration
is a function of reaction temperature T, initial H2S concentration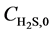 , time t, catalyst grain size R, and bed height z, while R is a function of t, whose analytic solution cannot be obtained easily. Equation (6) is usually a first-order differential equation and here it is solved using Crank-Nicholson’s method. Equation (5) is dispersed in the form of implicit trapezoid, and together with boundary conditions, a recursive equation set could be obtained as follows:
, time t, catalyst grain size R, and bed height z, while R is a function of t, whose analytic solution cannot be obtained easily. Equation (6) is usually a first-order differential equation and here it is solved using Crank-Nicholson’s method. Equation (5) is dispersed in the form of implicit trapezoid, and together with boundary conditions, a recursive equation set could be obtained as follows:
 (7)
(7)
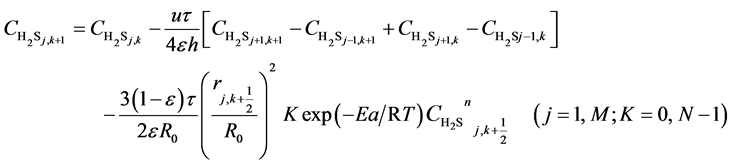 (8)
(8)
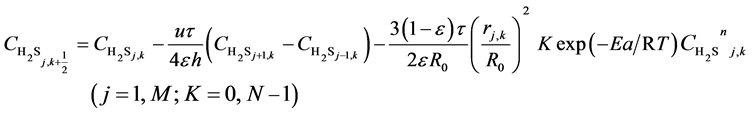 (9)
(9)
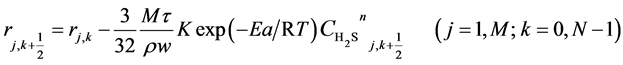 (10)
(10)
 (11)
(11)
Here, h is the bed step, τ is time step, subscript k is time grid, N is number of time grids, subscript j is axial bed grid, M is number of bed grids, and M + 1 is the bed virtual grid used in computation of the time point next to M. The target function is the minimum of sum of squared residuals between the experimental data and the model predicted values. The parameters in the intrinsic kinetic equations for presulfurization of hydrogenation catalysts are optimized and computed using a simplex method: activation energy Ea = 250.3 KJ∙mol−1, pre-exponential factor k0 = 1.2 × 1010 m∙K∙s−2, and reaction order n = 1.
3.2. Significance Test
The significance of the kinetics model was tested using F statistic, correlation coefficient, rank sum test [14] , and the absolute deviation between the experimental value and the model predicted value of H2S content at the fixed-bed’s outlet. Figure 1 shows the comparison between the experimental results and the model predicted results, and the straight line was y = x. Clearly, the experimental results and the predicted results under all experimental conditions were distributed evenly at two sides of y = x (Figure 1), indicating low general deviation and high consistence.
Table 2 shows the results of statistical tests. Clearly, the kinetics model obeys the requirements of rank sum test; F statistic is far larger than the critical statistic at the corresponding confidence level; correlation coefficient > 0.99; the difference between the positive and negative absolute deviations is not large and the average absolute deviation is 4.61%. All these results indicate that the kinetics mathematical model is significant.
4. Discussion
4.1. Effects of Temperature on f0
By solving the mathematical model, it is found that f0 is a function of temperature and reaction time. Since this functional expression is very complex and unsolvable, the effects of temperature and time on f0 are discussed separately.
Figure 2 shows the temporal changes of f0 with reaction temperature. Clearly, along with the rising temperature at the fixed time, f0 first decreases in the form of a power function and finally approaches 0 (Figure 2). For endothermic or exothermic reaction, the temperature rise at the initial stage would increase the reaction rate. But in the paper f0 decreases along with the temperature rise, and consequently, the increasing rate of reaction rate decreases with temperature rise. This is because during the presulfurization which is a gas-solid uncatalyzed reaction, the temperature rise will accelerate reaction, but on the other hand, as the reaction progresses, the porosity of the catalyst solid grains will decrease, manifested as shrinkage in large pores, blockage in small pores, and reduction in average pore size. The temperature rise will accelerate reaction and increase the conversion rate, but the resulting dense solid layer will block the gas diffusion and generally slow down the mass transfer and

Figure 1. Comparation H2S outlet concentration between the experimental value and predicted value.

Table 2. Statistical test of intrinsic kinetics model.
reaction rate, manifested as the decreasing f0 with the temperature rise. However, the effect of temperature on f0 is not significant compared with the effect of temperature on pre-exponential factor, and thus at the initial stage, the generally temperature rise will accelerate the reaction. With further temperature rise, f0 stabilizes and approaches 0, probably because the solid products block the catalyst’s pores more severely and thus control the whole reaction more effectively. When the resistance was infinitely large, f0 and thus the reaction rate were both 0.

Figure 3. Effect of sulfiding time on f0.
4.2. Effects of Time on f0
Figure 3 shows the changes of f0 with reaction time at varying temperature. Clearly, with the extension of reaction time, f0 decreases linearly and thus the reaction rate gradually declines. This is because at the initial stage, the fresh catalyst provided large reaction interface and thus the consumption of H2S per unit time increases and the reaction is accelerated. As the reaction progresses, the unreacted cores in the catalyst grains shrinks in radius, and the reaction surface area decreases in squared way; consequently, the solid products block the whole mass-transfer process and reduce the reaction rate. Moreover, the changing trend of f0 with time is smoother at high temperature than at low temperature, and f0 is smaller at the same time point (Figure 3). This is because sulfurization is an exothermic reaction; along with the temperature rise at the initial stage, the reaction rate is accelerated significantly, and thus a product layer is formed earlier on the surface of solid grains, which severely blocks the gas diffusion, and thus the effects of solid diffusion on reaction rate are enhanced. At the later stage, the temperature rise is unfavorable for the reaction, and the generating rate of solid residues is reduced. Thus, the blocking effects of solid residues on gas diffusion do not change much with the temperature rise. As a result, the f0 at different temperatures but the same time point changes slightly.
5. Conclusions
The theoretical and experimental investigations of the intrinsic kinetics of hydrorefining catalyst in ex-situ presulfurization have been able to arrive at the following conclusions.
1) The newly-built presulfurization kinetics model is significant with reasonable parameters.
2) The presulfurization of paraffin hydrorefining catalyst displays an activation energy of 250.3 KJ∙mol−1.
3) The presulfurization of paraffin hydrorefining catalyst displays a reaction order of 1.
4) In the newly built kinetic equation, f0 reflects the effects of solid diffusion on reaction, as f0 decreases along with the temperature rise or the extension of reaction time. The introduction of f0 into the intrinsic kinetic model makes the predicted results closer to the experimental values and thus increases the prediction precision.
5) The unreacted shrinking core model can reveal the presulfurization of single grains of a hydrogenation catalyst.
Acknowledgements
The authors are grateful to the Provincial Key Laboratory of Oil and Gas Chemical Technology of Northeast Petroleum University in China for financial support.