The World’s under Five Population—Do We Really Have Good Data of Its Size in Medicine? ()
1. Introduction
During the last decades, “forensic auditing” has opened a new way to take a quick look into important socioeconomic and demographic data. With the help of a mathematical tool, “forensic auditing” detects hints for operational inefficiencies, system flaws or deliberate fraud. This tool is called the “first-digit law”. The first-digit law, which is also called “Benford’s law” [1] , explains the frequency distribution in many naturally occurring data sets. Benford’s law is based on the observation that some numbers occur more frequently than others in various real life data sets.
Albeit Varian 1972 [2] suggested that Benford’s law could be used to judge the “honesty of purportedly random scientific data” [3] . In social sciences it remained virtually unused in this capacity for medicine. Some data in medicine have been investigated for their compliance with Benford’s law in medicine (e.g. on physical constants, death rates [1] and a pre-vaccination measles incidence in Preston, England [4] ), but it was almost neglected for what now appears to be of great value–—its ability to unmask questionable data sets.
Although the exact mathematics of Benford’s law is beyond the scope of our article, we would like to show that its intuitive correctness is easy to understand. A village with 10 children needs to double (to grow 100%) before the first-digit be replaced by a “2” (e.g. 20) as the first number for the number of the village’s children. The number of children than needs to grow by 50 %, so that the first number is replaced by a “3” and consecutively by only 25% to replace the first number by a “4”, so that it ends up in this example with 400 - 499 children. Another striking example is the money the villagers have on their account. When they have $100 in the first year growing by (theoretically) 100% each year, then all their accounts have a “1” in front for the first year. A “2” will be in front for the most part of the second year, but not for the whole year, because in the end of the second year it will be already a “4”—after two years of doubled income the villager would have $400. This shows that it is much easier—meaning here more frequent—to reach the lower numbers than the higher ones. This fact is addressed in Benford’s law, which shows that in many data sets the small numbers are much more prevalent than the higher ones.
Our objective was to investigate whether the important demographic; the number of children worldwide younger than 5 years old, is reliable enough to justify its use in the generation of other statistical data in the fields of medicine, public health, education and development.
We applied this law to published data of the world’s population younger than five years. This number is extremely important in medicine, public health and education, because it influences important political decisions, which affecting paediatrics (under five morality, infant mortality rate), public health (life expectancy, orphan rate) and moreover education (youth literacy rate, school participation).
In the light of recent successes to detect fraudulent data by this method (e.g. the socioeconomic data of the Greek government when entering the European Union [5] ) and the importance of a correct number for children younger than five years for various policies concerning sustainable development, we used Benford’s law to investigate the reliability of this numerical dataset.
2. Methodology
Mathematically Benford’s law states that the probability of a leading occurring number 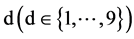 can be calculated through the following equation:
can be calculated through the following equation:
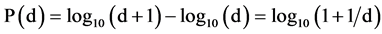 [3]
[3]
This distribution after Benford’s law shows that the number “1” occurs as leading number much more often than all other numbers—in around 30.1% of the cases; the number “2” in around 17.6%, the number “3” in 12.5%, the number “4” in 9.7%, the number “5” in 7.9%, the number “6” in 6.7%, the number “7” in 5.8%, the number “8” in 5.1% and the number “9” in 4.6% [3] .
The expected frequencies for the second, third and fourth number can be calculated in a similar way [6] . They show probabilities of their occurrence (now for the numbers 0 - 9) for the second digit between 12% for the “0” and 8.5% for the “9” and already for the fourth digit approaching an almost uniform distribution of 10% [7] .
Natural demographic data, covering more than two orders of magnitude, having no artificial cut-off point and providing more than five data in each group are likely to satisfy the law of Benford well [8] -[10] .
Data deviating and non-conforming with the probabilities of the law are therefore suspicious of systemic data challenges, arbitrary assignment of numbers, irregularities, psychological considerations, errors or plain fraud.
We applied Benford’s law to the available international data for one of the most important demographic indicators; the worlds under five population, which is widely used by important institutions. We used the data of each country in UNICEF’s survey “The State of The World’s Children” from Unicef’s reports of 2012, 2013 and 2014 (dealing with data from 2010, 2011 and 2012 [11] -[13] ).
In order to examine whether the deviation between the observed numbers and the expected numbers after the Benford law for first digits is at random or not we used the Chi-square test with an alpha value of 0.05, 8 degrees of freedom for each single year and 26 for the combination of three years. The null hypothesis (H0) was, that the numbers are correct (H1: There is a flaw in the numbers and they are not correct). In case the null hypothesis was not rejected we further scrutinized the data with the Benford law applied for the second digit (using an alpha of 0.05 and 9 degrees of freedom).
3. Results
1) Data evaluation: “The State of The World’s Children” from 2012-2014 [11] -[13] .
Data from 196 (2014: 197) countries were reviewed and all data concerning the world’s population younger than five years were counted manually for the frequency of the occurrence of all numbers from 1 - 9 in the first position. Results of observed and expected values are summarized together with the parameters in Tables 1-3 and graphically shown in Figure 1.
2) Direct comparison of the reported data.
3) Calculation of the significance of the findings:
For 2012, 2013 and the combined calculation 2012-2014 chi-square was higher than the cut-off value for the

Table 1. Summary of the observed values.

Table 2. Summary of the expected values.
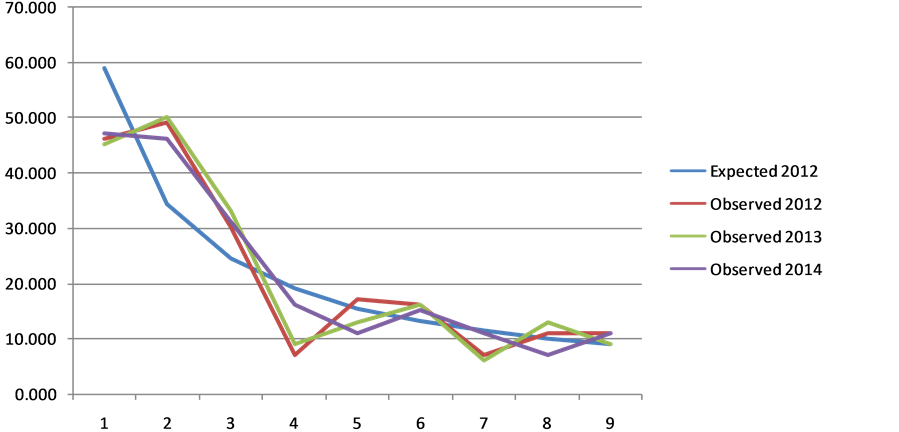
Figure 1. Observed and expected frequencies (Observed numbers from the reports 2012—14 for the first digit and expected values for the 2012 Benford distribution [the Benford distribution 2013 equals 2012 and for 2014 it is so similar that for the sake of the graph’s clarity it was avoided]).
chi-square distribution on a level of significance of 0.05 (alpha = 0.05) and the respective degrees of freedom [14] [15] . The null hypothesis had to be rejected.
In 2014 chi-square for the population younger than five years is 11.73 for the first-digit and 11.04 for the second digit. Being lower than the cut off the null hypothesis is accepted.
The rejection of the null hypothesis means that the numbers observed in the publication are not following Benford’s law for 2010, 2011 and for the three year period.
The acceptance of the null hypothesis for 2014 means that the numbers follow Benford’s law for 2014.
4. Discussion
Forensic accounting introduced the first digit law in order to scrutinize data sets to determine whether they are of natural origin or not [3] . When data sets are of natural origin, span several orders of magnitude and are not subject to artificial limitations they follow (for example in socioeconomic and demographic datasets) a distribution of their numbers, which was described as this “first-digit” first by Newcomb [16] , than by Benford [1] .
To our surprise the knowledge of this mathematical relation is not used widely in medicine until now. We are of the opinion that the first-digit law constitutes a valuable and quick tool to identify data-sets which need a closer scrutiny and it is a method, which is accessible to the clinician without the help of a trained statistician.
We used Benford’s law to scrutinize one of the most important data sets for policy making and programme evaluation in public health. Unicef publishes every year a report called “The state of the world’s children” [11] -[13] . Unicef considers this report as one of their “flagships publications” [17] .
The data from this report is used by international organizations, programme managers and legislators worldwide [17] . They all count on the accuracy of this data, collected and adjusted through a well known organization with a very good reputation.
Because in this article we could not scrutinize all the available data, we decided to choose the data for the size of the world’s population under 5 years of age, because this number influences many other important considerations such as the calculation of several other variables, ratios and parameters. In paediatric medicine and public health, the under five mortality, the incidence and prevalence of paediatric conditions or the life expectancy and the number of children needing to be fed in every major natural disaster are needed. In education, school attendance rates, population growth, the orphan ratio or the number of schools are examples of important indicators.
We were surprised to find that data in the reports of 2012 and 2013 significantly deviate from the expected values. The same is true for the compilation of the data from 2012 to 2014.
The Benford distribution only states this fact without offering an explanation or a reason for the deviation of the data from a natural distribution. But it shows that a deeper evaluation of the data is needed. The reasons can range from computational challenges or systemic operational discrepancies to psychological challenges or even conscious manipulation possibly influenced by struggle for international funding.
The data in the 2014 report was still quite different from the expected distribution (see Figure 1), but not significantly different from the expected values. Because of this discrepancy we evaluated the second digit for this data also and found the result confirmed.
An explanation for this sudden and significant change of the data quality in one year is not easily available, especially as Unicef did not supply us with any hint of a fundamental change in the way they collected their data for the 2014 report. If the change in data quality holds for subsequent years, then it is a very positive and laudable change. Nevertheless we would suggest that this data might be scrutinized by mathematically more demanding procedures such as the tests of Komolgorov-Smirnov and Kuipers [17] [18] which are outside the scope of this paper and its authors.
The purpose of this paper was to show that Benford’s law can be an indicator of when data needs more careful scrutiny, even when coming from well established sources and put together with care, expertise and experience. We wanted to raise awareness of the need for a certain degree of suspicion even towards established data sources, and that this evaluation tool is available and can be applied by the not statistically trained clinician.
The following limitations of our study need to be considered. Limitations to this study include the fact that two countries were classified as having no population under 5 years. For Niue this was a question of the initially used dimension (thousand), for the Vatican the reason is obvious. Some countries might be considered by scholars more as semi-independant territories and the status of other places, which are not incorporated, are not totally clear. 2014 was the first report which cited Southern Sudan as an independent country and therefore changed the first number without a change of data just through the existence of a new entity.
Nevertheless, we could raise the suspicion that this important data was not really reliable and accurate during recent years. Digital analysis through the Benford distribution has shown that data is not only imperfect due to the difficulties inherent in world-wide data collection, which we all appreciate (remote areas, dictatorships, no money to pay the collectors, computer challenges etc.)—but that there may be other systematic flaws, as is well known in other socioeconomic data (e.g. tax evasion [2] ), but this has not been widely discussed in medicine.
5. Conclusion
The data available on the number of children under five years of age living in this world seems not to be as reliable as it is sometimes thought. Despite some improvements in 2014, we should critically reflect the importance of this finding for future planning and funding in public health, medicine and education.