Some Properties of Analytic Functions with the Fixed Second Coefficients ()
1. Introduction
Let 
be the set of functions 
that are analytic in 
and normalized by
And let 
be the class of all functions 
that are analytic and have positive real part in 
with
.
Nunokawa investigated some properties of analytic functions which are not Caratheodory, that is, which are not in
. Furthermore, he has found the order of strongly starlikeness of strongly convex functions in 
(see: [1] [2] ).
Now, for a fixed
, let 
consist of functions 
of the form
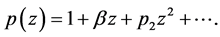
And let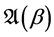 
consist of analytic functions 
of the form
where the second coefficient 
is fixed constant.
In [3] [4] , Ali et al. have extended the theory of differential subordination developed by Miller and Mocanu [5] , to the functions with fixed second coefficients. And Lee et al. [6] and Nagpal et al. [7] have applied the results, to obtain several extensions of properties for univalent functions with fixed second coefficients.
In this paper, we investigate some argument properties for analytic functions 
with fixed second coefficients and positive real part. And we apply our results to the normalized univalent functions with fixed second coefficients.
We need the following Lemma for functions with fixed initial coefficient.
Lemma 1 [3] Let 
and 
be continuous in
, analytic in 
with 
and
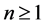. If
then
and 
where
(1)
Here, we note that the inequality (1) implies that
since
.
2. Lemmas
Lemma 2 Let 
be analytic in 
and 
in
. Suppose that there exists a point 
such that
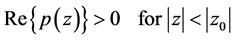
and
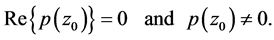
Then
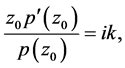
where 
and
.
Proof. Let us put
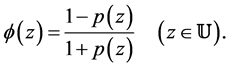
Then
, 
for 
and
. And we note that
By Lemma 1, we have
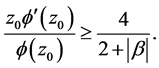
Hence
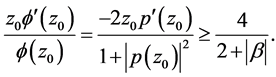
And this inequality implies 
is a negative real number which satisfies
Now, we put
. For the case
,
(2)
For the case
,
(3)
Hence, by (2) and (3),
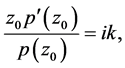
where 
and
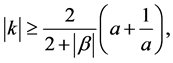
Hence the proof of Lemma 2 is completed.
Lemma 3 Let 
be analytic in 
and 
in
. Suppose that there exists a 
such that
and
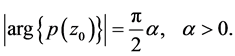
Then
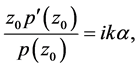
where
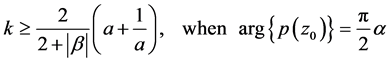
and
with
Proof. Let us put
Then
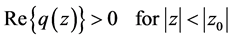
and
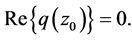
Let us put
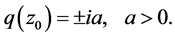
Applying Lemma 2, we get
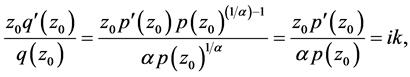
where 
with
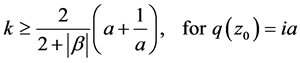
and
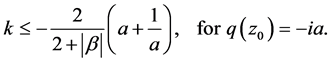
3. Argument Estimates for Functions with Fixed Second Coefficient
Theorem 4 Let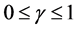 
and 
satisfy
Then
where
(4)
Proof. Suppose that there exists a point 
such that
and
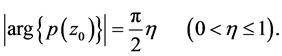
By Lemma 3, we can obtain that
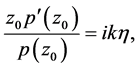
where
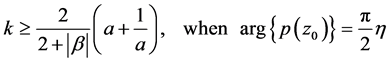
and
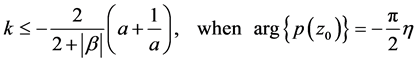
with
. For the case
,
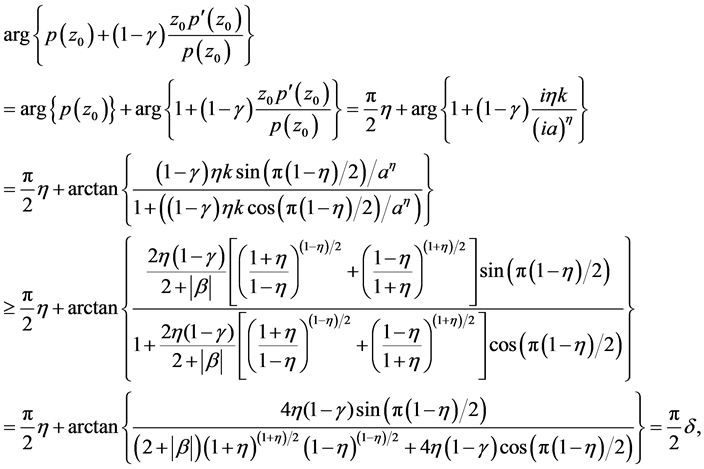
which is a contradiction to the assumption. For the case
, using the same method, we can obtain a contradiction to the assumption.
Remark 5 If
, then Theorem 4 reduces the result in [[8] , Theorem 3].
Theorem 6 Let 
and 
satisfy
(5)
Then
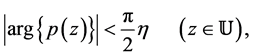
where
(6)
Proof. If there exists a point 
such that
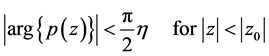
and
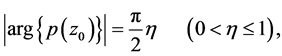
then Lemma 3 gives us that
If
, then we have
. Therefore, we see that
with
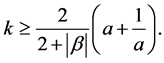
Hence
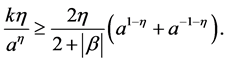
Now, we define a function 
by
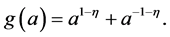
Then
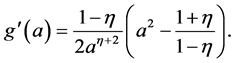
Hence 
takes the minimum value at
. Therefore,
Thus we have
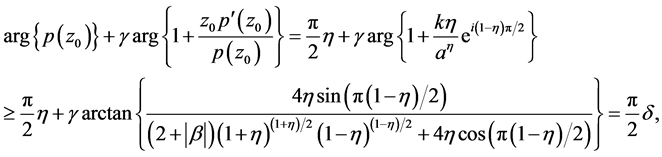
which contradicts the condition (5). And if
, applying the same method we have
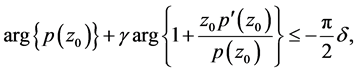
which contradicts the condition (5). And this completes the proof of the Theorem 6.
Remark 7 If
, then Theorem 6 reduces the result in [[8] , Theorem 1].
Theorem 8 Let 
and
(7)
for some
, 
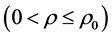
, where 
is given by
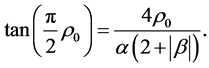
Then
Proof. Suppose that there exists a 
such that
and
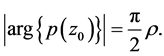
By Lemma 3, we can obtain that
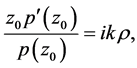
where 
with
and
For the case
,
(8)
since
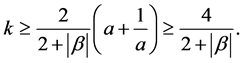
Now, we define
Then
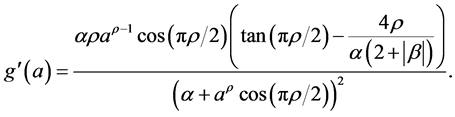
Define
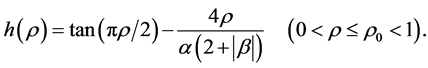
Then 
and
. Furthermore,
for all
. Hence 
for all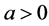
. And
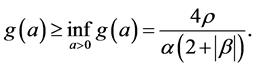
By (8), we have
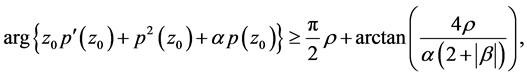
which is a contradiction to the hypothesis. For the case 
, using the same method, we can obtain a contradiction to the assumption.
Remark 9 If
, then Theorem 8 reduces the result in [[9] , Theorem 2.1].
4. Corollaries
For a function
, 
is called strongly starlike of order
, 
, if
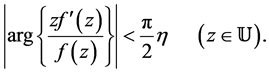
And 
is called strongly convex of order
, 
, if
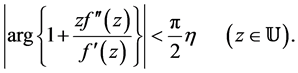
Using these definitions and Theorem in Section 3, we can obtain the following corollaries.
Corollary 10 Let 
and
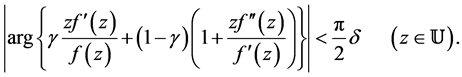
Then 
is strongly starlike of order
, where 
is given by (4).
Putting 
in Corollary 1, we can obtain the following Corollary.
Corollary 11 Let 
be a strongly convex function of order
. Then 
is a strongly starlike function of order
, where 
is given by
Corollary 12 Let 
and 
satisfy
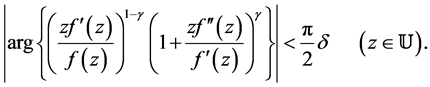
Then 
is strongly starlike of order
, where 
is given by (6).
Corollary 13 Let 
and
where 
is given by (7). Then 
is strongly starlike of order
.