Perspective of Adaptive CN System for Forecasting Congestion of Road Traffic Flow ()
1. Introduction
It is clear that present road traffic networks and communication networks (CN) have not well cooperated. The answer is obvious: Simply we can say that we haven’t had the essential core scientific knowledge concerning the road traffic flow. Since the author has well analyzed the road traffic dynamics [1] , he will be able to challenge the difficult subject that has long time been left behind. The subject is the problem concerning the CN for road traffic flow management system. The most important subject to be solved is how to forecast or avoid the traffic congestion. If the congestion was forecasted, the traffic flow management should make an action to suppress the congestion and to go to the highest efficient transportable road system from the economical viewpoint.
CN is inevitable and has contributed to our present society and no exception of the road traffic system. We have at present a big system of the Global Positioning System (GPS) which has been applied to the Car Navigation System that is operated by huge CN. Today’s navigation system does not have a forecasting ability. The most necessitated subject for the traffic management is the traffic forecasting system. If the forecasting ability is applied, we may have a counter method against the congestion.
If the traffic situation could be forecasted, the adaptive sign boards may be available and the intelligent sign board will be possible. Viewing from the CN, those are not high technology. The role of CN has not been sufficient to meet such a demand. We need more sophisticate ways to give the information to drivers as prompt as possible and let every driver know the short term forecasted traffic situation.
Since the traffic flow situation can change so fast, it becomes quite different one after 30 seconds as we always experience. Thus the informed past knowledge of traffic congestion cannot be useful for present drivers. We need forecasted information about congestions that may occur in very near future. But today’s road management cannot do it, because today’s delivering traffic information is the past stochastically analyzed one that cannot estimate the near future traffic situation. Many researchers have noticed this point. The author picked a reference up here which surveyed the published papers concerning short term forecasting of road traffic flow [2] . Viewing from the papers published, they are much the same and they are too sophisticated to be practical.
In order to make a cooperation between road traffic management and CN, the author firstly should mention the essence on the theory of road traffic flow based upon the Weber-Fechner Law (WFL) [3] [4] .
The key parameter is the speed  (characteristic speed), which will be mentioned in 2. And the speed
(characteristic speed), which will be mentioned in 2. And the speed  is the speed that gives the maximum transportation volume (the most economically efficient flow).
is the speed that gives the maximum transportation volume (the most economically efficient flow).
Before discussing the CN to be applied, we need to get the knowledge of the road traffic behaviors. Thus as the first step, we shall see the related theories on the road traffic flow. The first step is to obtain the characteristic speed which is designated by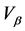 . The most efficient speed is
. The most efficient speed is .
.
2. Characteristic Speed 
2.1. WFL Equation in Road Traffic Flow
WFL is the psychophysical law (history: [3] , brief explanation: [4] ) that was discovered in 1834 and 1846 [3] . The law mentions the relationship between stimulus and sensation (e.g. eye(s) senses the outside image as a stimulus, and feeling of speed in a moving vehicle as a sensation). The formulation of the stimulus-sensation relationship is as follows: “the sensation is proportional to the logarithm of the stimulus level”.
From observing the road traffic flows, the author discovered the relationship between the distance-headway between subsequently moving vehicles (distance from head to head), which is denoted by X (X1 and X2 in Figure 1(a)) and speed V can obey the WFL. Then the exponentially it can be written like
 (1)
(1)
X: distance-headway in meter (m)
X0: X at V = 0 V: speed (m/s)
β: constant (s/m)
According to our observation, the average of  is about 7 - 15 m. β is a constant that depends on the quality of road; smaller β shows a good road.
is about 7 - 15 m. β is a constant that depends on the quality of road; smaller β shows a good road.
Although the original formula of law is logarithmic one, the author rewrites it like (1), because the mathematical discussion is easy to develop.
Our discussion will follow the MKS units.
X can be determined by
 (2)
(2)
where T is the time-headway (time difference between subsequently moving two vehicles).
Vβ was defined from βV = 1 in (1) like
 . (3)
. (3)
2.2. Flow at Speed of 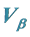
Vβ is the boundary speed of free flow and congestion. When the vehicle speed V is smaller than Vβ (V < Vβ), the flow becomes congestion, and when V > Vβ, the non-congestion flow is guaranteed. In this subsection, we should know it theoretically. At this condition of V = Vβ, X will be
 (4)
(4)
Since 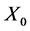 is 7 - 15 m, (4) becomes about 20 - 45 m. We shall see the flow of Vβ.
is 7 - 15 m, (4) becomes about 20 - 45 m. We shall see the flow of Vβ.
The row of vehicles has a tendency to make a bunching flow as shown in Figure 1(a) which shows the flow is going to bunch. Due to the driver’s general behavior, both X1 and X2 will soon become , and final flow becomes like that shown in Figure 1(b), of which speed becomes Vβ. Figure 1(b) can also appear in case of green signal flow at an intersection which is the forced laminar flow.
, and final flow becomes like that shown in Figure 1(b), of which speed becomes Vβ. Figure 1(b) can also appear in case of green signal flow at an intersection which is the forced laminar flow.
We should note that the distance-headway X becomes eX0 (20 - 45 m) at this condition.
l There is a flow simulations referring to the liquid flow. If we take this idea, the flow shown in Figure 1(b) can be said the laminar flow. In case of traffic laminar flow, Vβ can be called critical speed. But since the value of Vβ can differ from place to place even on the same road, then it was also defined as the characteristic speed of road.
2.3. Behavior of Flow at Vβ
As mentioned above, Vβ is the speed of vehicle row at the condition of laminar flow as shown in Figure 1(b). This type of flow may be only theoretical and cannot continue for long time because this condition strictly forces the drivers to obey to move with the speed Vβ. Thus the situation shown in Figure 1(b) cannot be maintained long time and length of row must be limited. And if the speed becomes less than Vβ (V < Vβ), the speed of vehicle row goes to congestion and the distance-headways approach to  (7 - 15 m). That is to say:
(7 - 15 m). That is to say:
1)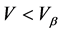 : Toward congestion 2)
: Toward congestion 2) : Free flow
: Free flow
2.4. Determination of Vβ from Actual Flow
Vβ is the only parameter to be used for controlling the traffic flow. But we should know how Vβ can be determined from the practical measurements. As mentioned just end of the above 2.2 (●), Vβ is not the inherent parameter of the road, and it may have different values at the different places along the road.
Here we should admit to refer the essence in the author’s derived algorithm to determine it as follow:
 (5)
(5)
Vtav: Total average of V (speed)Ttav: Total average of T (time-headways)T<3: Average of time-headways less than 3 seconds.
Details of the above have been mentioned in p. 56 in [1] . Each parameter mentioned above can be determined by measuring many vehicles at the specific position of road which should include curves, slopes or impairments, etc. Note that when Ttav = T<3, Vtav = Vβ. When the time-headway T becomes T<3, the flow becomes laminar one as shown in Figure 1(b).
The example of the actual values of Vβ that calculated from (5) is shown in Table 1.
2.5. Natural Appearance of 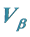
Figure 2 shows how Vβ can naturally appear in case of vehicles moving from flat to up-slope portion of a road. The flow speed declines unconsciously when vehicles encounter the up-slope from flat portion. The decline of speed can occasionally be Vβ like that shown in Figure 2, which is just before the congestion. If the speed farther declined and became less than Vβ, the flow becomes congestion and distance-headways should be  as shown.
as shown.
2.6. Congestion
There are two types of congestion: One is natural and another is artificial.
3. Natural Congestion
3.1. Driver’s Sensation
Each driver has a common sensation (habit) to follow the foregoing vehicle as close as possible. The process of appearance of laminar flow is shown in Figure 1(a), in which the distance-headway X1 and X2 are both decreasing and finally all distance-headways become  in average. If this row of
in average. If this row of 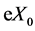 became long enough, the row of flow becomes quasi-laminar flow like Figure 1(b) and the speed becomes V ≒ Vβ.
became long enough, the row of flow becomes quasi-laminar flow like Figure 1(b) and the speed becomes V ≒ Vβ.
Since the laminar flow cannot permit disorder, when the speed of any one of the vehicles deviates due to driver’s sensation, the laminar flow may be destroyed and the flow goes into congestion.
3.2. Up-Slope
A typical example is shown in Figure 2. The vehicle speed decreases when it encountered an up-slope portion of road from flat portion. The figure shows the case where the speed became a critical speed of Vβ. This phenomenon occurs unconsciously, more speed retardation becomes the cause of the congestion.
Since the time-headway T cannot change with the slope, if we denote both decreasing amount of X and V are 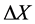 and
and , respectively, from (2)
, respectively, from (2)
 . (6)
. (6)
At the slope, the distance-headway X becomes . Figure 2 shows the case of
. Figure 2 shows the case of
 . (7)
. (7)

Table 1. Example of values of Vβ for different road.
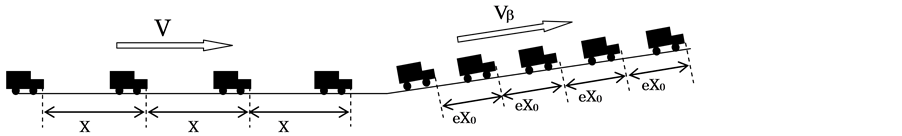
Figure 2. Natural appearance of Vβ by up-slope (distance-headways at flat portion were averaged and shown as X).
If  becomes a little bigger, the distance-headway becomes smaller than eX0, and the flow goes into congestion.
becomes a little bigger, the distance-headway becomes smaller than eX0, and the flow goes into congestion.
4. Artificial Congestion
A typical artificial congestion is the case of intersections. In this case the flow becomes the series of bunched flow like that shown in Figure 1(b). The one lane alternative flow is also the same in case of road impairment or accident. The same phenomena may occur with the case of up-slope mentioned above 2.
l I. Taking into account of (2), (1) can be written like
 (8)
(8)
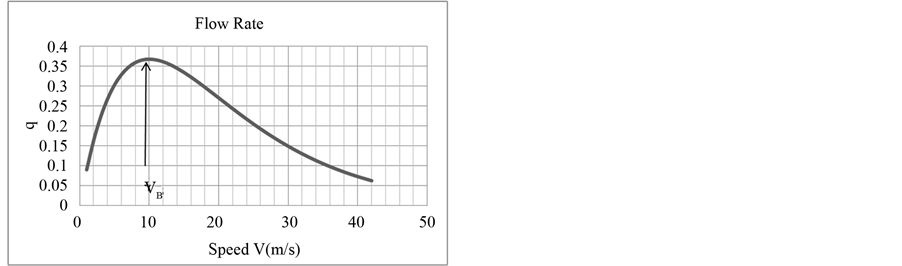
from dT/dV = 0, we can derive the minimum T; (Tmin), at V = Vβ. Then qmax (=1/Tmin) is the maximum flow. See the graph that shows V = Vβ gives the maximum flow rate.
We should note that the driver can control the speed V only. The Weber-Fechner Law can be applied when X is considerably small, for example X < 300 m for expressway and X < 150 m for the other road.
l II. Transportation Volume Q and Optimum Speed Definition: . (9)
. (9)
From (8),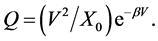 (10)
(10)
From  Maximum Q, (Qmax), can be obtained at
Maximum Q, (Qmax), can be obtained at
 (11)
(11)
The maximum transportation efficiency can be obtained at the condition of (10). See the graph.

5. CN System for Forecasting of Traffic Flow
5.1. Role of CN for Traffic Managements
In order to realize the non-congesting traffic, a short term forecasting system and optimization of road traffic flow are essential. The tactics are as follows:
1) Send the bottleneck (smallest Vβ) in the specific road span via CN.
2) Suggest the driver the recommended speed of 2Vβ via CN.
3) Send the message to drivers of both 1) and 2) from Control Center via CN.
We know from ●I that the maximum flow rate (qmax) can be attained at the speed of Vβ. And the maximum transportation volume (efficiency) can be obtained at 2Vβ (●II). Then we should add 4) as 4) Indicate speed of 2Vβ as the limit of speed via CN.
Those messages can be shown by the sign boards at the roadsides, which should be adaptively changed.
5.2. Forecast of Flow
We need the measured data of each vehicle speed V and time-headway T. Those measurements can be carried out by sensors and the results are sent via CN to the Center (Traffic Information Center) which processes the data and the necessitate information should sent to the sign boards on the road side.
Figure 3 shows the assumed Vβ’s obtained from (4) by the measured data (V and T) of vehicles. This typical figure shows the road span in which it has three slopes as shown. Each slope has the inherent Vβ and we assume here the magnitude of Vβ is like that shown as
 . (12)
. (12)
That is, the smallest one is  which means the slope of the span 2 - 3 in Figure 3 has the smallest Vβ.
which means the slope of the span 2 - 3 in Figure 3 has the smallest Vβ.
As we have seen in 2.5, if the flow rate q is increased, the congestion shall begin at the smallest Vβ portion on the road, and in this case  is the smallest of which portion is the span 2 - 3.
is the smallest of which portion is the span 2 - 3.
By knowing the above in advance, the traffic flow can be forecasted or estimated. If we measure the flow at far behind portion of which Vβ is larger than , we can forecast that the flow at the portion of 2 - 3 span is going to congestion or not.
, we can forecast that the flow at the portion of 2 - 3 span is going to congestion or not.
l Vβ at intersection is similar with that shown in Figure 3, which is shown in Figure 4.
Each span between intersections has an inherent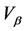 , but it may depend on the signal periods or patterns. However in principle, we can treat the intersections as the same with that shown in Figure 3.
, but it may depend on the signal periods or patterns. However in principle, we can treat the intersections as the same with that shown in Figure 3.
5.3. CN System of Data Process for Traffic Flow
Figure 5 shows the conceptual image of CN system. The key essence is as follows:
1) Sensing the data by sensors (S1,S2) at both portions: S1 at the biggest Vβ and S2 at the smallest Vβ.
2) The data (speed V and time-headway T) are sent to DP (data processing) Sub-center which carries out the time sequentially averaging of both V, T and flow rate q.
3) The results are sent to the Center.
We can also say the system shown in Figure 5 is the road traffic forecasting system, because the sensor S2 in

Figure 3. The bottleneck is the span 2 - 3 which has the smalllest Vβ.
Figure 5 is watching the flow at the weakest portion (bottleneck; smallest Vβ), which means the first congestion occurs at this portion when flow rate (density) increased. The data of S2 are real timely processed at the DP Sub-center. The Center should disseminate it far behind Sign Board that every driver looks at. If we see Figure 5, moving vehicle on the flat portion (far behind of bottleneck) can see in advance the possible congestion peril.
5.4. Adaptive Sign Board
Figure 6 shows the conceptual image of the adaptive road traffic flow management with CN system.
The contents should be as follows:
1) Speed limit: 2Vβ, because this speed gives the most economical benefits.
2) Existing of congestion: place.
3) Accidental bottleneck: place.
The disseminating the above information to drivers concerning present state of the traffic flow over the area should be very useful. The system shown in Figure 6 can operate to meet such needs. The roadside sign board can adaptively be changed in a short term, for example every 30 sec.
In Figure 6, The Speed Sign Board shows the recommended speed (speed limit) that should be changed timely from the Center. The Information Board can indicate the information concerning flow management, for example, the reason of speed limitation.
6. Conclusions
Firstly, we should notice that the road traffic phenomena are not complicated, because the author has cleared this fact by finding that the relationship between distance-headway and speed obeys the Weber-Fechner Law that is shown in (1).
We have seen in this article that the important role of Communication Network (CN) in road traffic management and control. The summarized results are as follows:
1) Definition of characteristic speed of road by .
.
This speed is the critical speed of moving vehicle row with the highest density, and theoretically, if the row speed becomes less than Vβ, the flow goes to congestion.

Figure 5. CN system for data acquisition and processing of traffic flow.
2) Finding 
The most economically effective flow speed.
3) Importance of Sensor and Communication Network (CN)
The CN is inevitable for making the adaptive road traffic flow management by the short term forecasting.