Optimizing Query Results Integration Process Using an Extended Fuzzy C-Means Algorithm ()
1. Introduction
In the past few years, the amount of data manipulated daily has increased dramatically, and will continue to increase exponentially with the huge insertion of data throw social networks, e-commerce web sites and even in big services companies, such as hotel chains.
In data warehousing, we can find several architecture types; the first with one data warehouse, where data are extracted from sources, transformed and then loaded into it; even though, dirty data can steal in, and disturb the decision making. The second architecture, is based on multiple data warehouses that could be distributed, as a result of vertical, horizontal or other type of DWs fragmentation. We can also find architectures based on a set of data marts, in this case, data sources are integrated between each other. Another case of study is based on federated heterogeneous, autonomous and physically separated data warehouses which are seen as a single component to the final user. In multiple DWs based architectures, the user writes his query in a specific query language then the query is partitioned into several sub queries to be executed over the disparate, heterogeneous data warehouses. The next step consists of the integration of the query results into one formulated result responding to the user query.
During the results integration process, one of the major problems in this phase is to eliminate duplicated data sets, not only syntactic duplication but also semantical, from which a classification process can be used.
Researches studies are maintained in order to improve solutions to data cleaning and data redundancy elimination, by introducing new algorithms based on statistical solutions such as [1] .
Many works focused on algorithms like Naive Bayesian algorithms, decision trees or SVM. Others focused on combining two algorithms to create a new classification algorithm [1] .
Unfortunately, most of these solutions show their limits in large data sets or Olap queries case and do not treat efficiently the semantic redundancy problem, like using Naive bayesan algorithm that has strong feature independence assumptions and there are no large data sets as input.
Using SVM, Naive bayesean or decision trees is not suitable in the case of records from multiple domain; they are generally used for multiple data bases from single domain but provide limited results.
Thus, to fill this gap, we are going to propose a solution based on proposing an improved FCM (fuzzy C-means) classification algorithm by using topic ontology.
The novel algorithm allows finding similarities and classifying heterogeneous data that represent the same entity of reality but differently, classify the hierarchical items in order to represent the degree of aggregation in the OLAP queries results, and this is by reducing the number of iterations and the recalculation of clusters centroids referring to precalculated matrix.
So, in the second section, we are going to present an overview of the most popular existing works related to this topic, then in sections 3 and 4, we will introduce the improved FCM algorithm and give some experimental results and comparison with the standard FCM algorithm. Then, in Section 5 we discuss the perspectives and future works to be done.
2. Recall of the Fuzzy C-means concept
The fuzzy C-means algorithm was developed by C. Bezdek in 1983 [2] [3] . It aims to regroup any sets of numerical data into classes or clusters, after an iterative process, so the items in the same class are as similar as possible, and it may to an item to belong to two clusters with different membership degree between 0 and 1.
The use of this algorithm was basically for pattern recognition [4] [5] like detection of spam e-mails and it is recently used for applications such as link spam detection [6] , Then used for image segmentation, modeling and identification .
The FCM is a fuzzy clustering algorithm based on the optimization of a quadratic criterion of classification, where each class is represented by its center of gravity.
The algorithm requires knowing the number of classes in advance and generates classes through an iterative process by minimizing an objective function.
The first step is to specify as input the number of clusters, but it still anunsupervised algorithm.
Then initializing randomly the partition matrix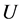 , which contains
, which contains 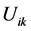 items , where
items , where 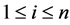 is the number of the ith element with
is the number of the ith element with 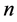 the total number of items, and
the total number of items, and 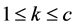 is the kth cluster with
is the kth cluster with 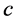 the total number of clusters .
the total number of clusters .
Each 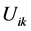 represents the membership degree of the ith item to the kth class (between 0 and 1).
represents the membership degree of the ith item to the kth class (between 0 and 1).
Technically, every item has a membership degree with every cluster, but it has a strong connection with one than another.
To insure good portioning, the 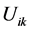 items must satisfy the conditions bellow:
items must satisfy the conditions bellow:
1) 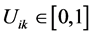
2) 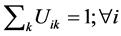
After initializing the partition matrix, the next step is to recalculate the new centroids for each cluster and update the membership degrees.
To normalize the 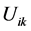 linearly to make their sum equal to 1, the FCM uses a parameter
linearly to make their sum equal to 1, the FCM uses a parameter 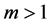 generally initialized at 2.
generally initialized at 2.
The equation used to revaluate the membership degrees is:
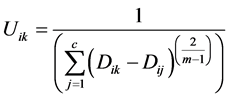 (1)
(1)
and the equation used to recalculate the {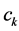 } centers is given as follow:
} centers is given as follow:
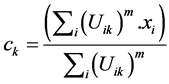 , (2)
, (2)
with 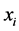 is a vector representing an item from the data set.
is a vector representing an item from the data set.
The FCM uses equations (1) and (2) in an iterative process until the value of:
![]()
where ![]() is a minimized objective function used to revaluate the partition matrix, and defined as:
is a minimized objective function used to revaluate the partition matrix, and defined as:
![]() (3)
(3)
![]() is a parameter used to control the breakpoint of the iterative process.
is a parameter used to control the breakpoint of the iterative process.
3. Problem with the FCM algorithm
when we analyzed the FCM algorithm, we found that it is sensitive to the number of cluster as input, and depends on the context, also it could not treats non numerical values, so in our case; query results integration, the values could be textual or numerical which represents a problem.
The fuzzy C-means algorithm combines local and global information in the computation of relative fuzzy membership function which makes it take more time in clustering process.
That’s why we thought that we can improve it by improving the execution time of its sensitive points: calculation of the partition matrix, the initializing of the number of clusters and the update of the partition matrix and recalculation of new centroids.
4. Presentation of the solution
4.1. What Is topic ontology and how it works?
An ontology as defined by [7] ; is an explicit specification of a conceptualization, it is shared understanding of some domain of interest and a shared uderstanding of some domain interest. Several methodologies has been developed to solve the integration issue, one of them is the use of ontology, which founded in the field of philo- sophy.
Three approaches are found in using ontology in data integration process, as shown in [8] : Single ontology approach; which use a global ontology shared between all the heterogeneous sources, the second approach is the Multiple ontology approach, characterized by the usage of local ontology for each data source. Every data source has his own ontology and its integrated in harmony with the others. the problem in this case, is that by using many local ontologies we are facing the same problem as the first one, if they are not sharing a common vocabulary, we need to define ontology for the set of local ontologies. The last approach is called hybrid ontology approach, this one seems to be the more convenient for big projects, in which data sources may be extremely different, so it propose to use a shared vocabulary to integrate local ontologies that are defined on each data source.
There are many types of ontologies: Top-level ontlogy: describe very general concepts like time, space, which are independent of a particular problem or domain [9] , Domain ontology, Task ontology, and topic ontology: these are the most specific ontologies, concepts in topic ontologies are described in a application language and a specific domain vocabulary.
The used system is based on integrated topic ontology in a federated heterogeeous data warehouses, the system architecture is described as bellow:
Every component as shown in (Figure 1), may have his own local ontology, these local ontologies are integrated into one global ontology used in query processing and in the construction of the global federation schema. This system is using SQL as a high level query language to formulate user query.
4.2. Our contribution
The experiments discussed in this paper have been tested in a context of disparate heterogeneous data warehouses, on which users want to execute queries despite the location or the representation of data.
Every component has his topic ontology then the local ontologies are included into one global topic ontology to rely to the semantic problems during the query reformulation, the system contains a data localization map that locates the components where the data wanted is, as we presented in previous paper [10] .
After locating data and rewriting sub queries from the initial user query, the results must be integrated into one final result to answer the initial query. In this phase, the problem that persists is how we can integrate data from different sources knowing that they have different structure, semantic and representative form. So in this case we have to find a solution to clean data by eliminating redundancy and reformulating data sets in a standardized form applying the aggregation functions stored in repository.
The queries manipulated in this work are OLAP queries, executed over multiple data warehouses in hotelier domain. The problem that occurs during the query processing, is that after the results integration, the data sets may contains duplicated data; by duplication we mean semantic duplication, since the data warehouses are heterogeneous, we may have two results represented differently, but in fact they refer to the same entity of reality. We can also face the presence of incomplete information during the results integration, the outlier’s problem, and the loss of information in case of different aggregation level between sources; in this case we take by consideration the hierarchical dimension of data.
To fill the gap of data duplication elimination, we have chosen to apply the FCM as an unsupervised clustering algorithm and improve it by using the topic ontology that we already have in our system.
By studying the FCM algorithm and the different applications where it was used, we found that we can apply it in data sets cleaning process in heterogeneous OLAP results and optimize it to give more efficient results.
To improve the FCM algorithm, we first thought improving the partition matrix first initialization by using the data dependency table (Table 1), which represents the dependency between every elements of the global ontology, and dependency degree based on the RDF representation of data as triples
the degree is automatically assigned during the creation of new item in the global ontology it is equal to 1 if two items are synonyms , 0 if they have no relationship and the level in the hierarchy if it is super or sub classes.
![]()
Figure 1. Data warehouses federation management system using ontology.
Calculating the number of clusters
The first intervention in the improvement process of the FCM algorithm was by fixing the total number of clusters ![]() as a calculated input, since the first problem that diminish the performance of this algorithm is that its sensitivity to the number of clusters that generally initialized randomly, so either the number of clusters decreases by merging classes or increases by creating more classes or groups (called also clusters).
as a calculated input, since the first problem that diminish the performance of this algorithm is that its sensitivity to the number of clusters that generally initialized randomly, so either the number of clusters decreases by merging classes or increases by creating more classes or groups (called also clusters).
In our case and to optimize the performance of the FCM algorithm we first fix the number of clusters attributes from the initial user query plus for each one we add three classes, one representing sub class category and the second representing the super class category of the class in question and the last one represents the synonyms class. For example, if the user query is:
SELECTA, B
FROMF, D1, ..., Dn
WHERE C1 AND C2
GROUP BYB
HAVINGCn
ORDER BYO
We have for the attribute A, three classes, and the same thing for the attribute B. So the number of initial clusters is fixed for each attribute.
By calculating the degree of similarity between attributes, the second step is to calculate the degree of similarity between records formed by these attributes, so the redundancy detection becomes easy.
by using the proposed method, the initializing of the partition matrix based on the RDF matrix takes less time than with the existing FCM algorithm (Table 2), and the iterative process to update the partition matrix is also executed in optimized way .
The type of redudancy tested in our work is the semantic redundancy, since we used a topic ontology to refer to, in case of ambigus conflict between data, during the integration process, the improved FCM algorithm could cause an agressivedata redundancy elemination, due to an ambigus criteria extracted from the topic ontology, and then clustering unredundent items.
In a future work, we count implementing a verification step during the clustering phase , to avoid this problem.
5. Conclusions
![]()
Table 1. Relation between concepts (RDF Matrix).
![]()
Table 2. Performance comparison between the improved and the unimproved FCM algorithms.