Propagation of Dark Solitary Waves in the Korteveg-Devries-Burgers Equation Describing the Nonlinear RLC Transmission ()
1. Introduction
In recent years, nonlinear discrete system has received considerable attention. There are two main reasons for this interest: the development of experimental techniques making it possible to realize experiment in complicated periodic nonlinear structure and the potential for all-optical switching applications. The nonlinear electrical lines are very convenient tools for studying quantitatively the fascinating properties of wave propagation in nonlinear dispersive media [1] [2] . In particular, they provide a useful way to check directly how the nonlinear excitations behave inside the nonlinear medium by means of probes related to an oscilloscope. The first studies of soliton on electrical lattices have been done by Hirota and Suzuki [2] . Qualitatively, the origin of soliton in nonlinear electrical line is explained by the balance between the effect of dispersion (due to the periodic location of capacitor in the nonlinear electrical lines) and nonlinearity (due to the voltage dependence of the capacitance). The nonlinear transmission lines (NLTLs) are discrete systems but approximate the continuum system quite well, as will be seen below [1] [3] . The NLTLs provide a useful way to check how the nonlinear excitations behave inside the nonlinear medium and to model the exotic properties of new systems [3] . Depending on device technology and design, NLTLs can easily be fabricated and integrated with resonant tunneling diodes (RTDs) using InP technology [4] [5] . Let us also point out that, recently, NLTLs have proven to be of great practical use in extremely wideband (frequencies from dc to 100 GHz) focusing and shaping of signals [6] which is usually a hard problem. Various investigators have discovered the existence of solitons in NLTLs, through both mathematical models and physical experiments. Interestingly, in constructing proposed nonlinear RLC network, we were motivated with a very interesting example of nanobio electronics problem. Namely, Sekulić et al. [7] have recently modeled ionic currents along microtubules in the eukaryotic cells, they have analytically analyzed the possible use of microtubules as protein structure for building biomolecular nanoscale NLTLs in the context of the polyelectrolyte character of these cytoskeletal filaments [8] . Solitary wave propagation is one of the important phenomena associated with the NLTL. It has been analyzed theoretically that there could exist solitary waves with both bright and dark soliton solutions in the NLTL with nonlinear element replacing the loaded shunt inductors or the shunt capacitors [9] -[11] . Many soliton equations describing nonlinear systems are known and solitons themselves have been observed (directly or indirectly) in various media. However, there are only a few systems where solitons are easily and directly observed in controlled laboratory experiments. So, finding exact solutions is important to understand the mechanism of the complicated nonlinear physical phenomena. In the recent decade, several methods for finding the exact solutions to nonlinear equations of mathematical physics have been proposed, such as trigonometric function series method [12] , the modified mapping method and the extended mapping method [13] [14] , homogeneous balance method [15] , tanh function method [16] , extended tanh function method [17] , hyperbolic function method [18] , rational expansion method [19] , sine-cosine method [20] , Jacobi elliptic function method [21] , F-expansion method [22] , and so on. Our goal is to present a method to computational study of solitary waves in nonlinear RLC transmission lines. A circuit model of a NLTL with N identical cells is given in Figure 1. The series inductance is due to magnetic field effects, and the capacitance is due to electric field coupling between the lines. The losses in the transmission media are depicted by the series and the shunt resistors. These resistors represent the finite conductivity of the conductors and the dielectric insulator between the conductors, respectively. The resistors r1 and r2, accounting for the transmission line losses, the linear inductance L, and the voltage-dependent capacitance C(Vn) are the circuit parameters. The resulting circuit is referred to as a distributed model of a nonlinear RLC transmission lines.
In this work, after writing the discrete equation of the NLTL trough the Kirchhoff’s laws, we apply the perturbative method to reduce the previous equation to the well-known KdV-Burgers equation. This equation has solitary wave solution namely the dark soliton. Then we numerically investigated the propagation of this dark soliton through the line. Numerical investigations show also the impact of the dissipation on the soliton and the possible chaotic behavior. The remainder of the paper is organized as follows: in Section 2 we present the model of the NLTL understudy and we derive the equation governing modulated waves in the network. In Section 3, numerical simulations confirm the propagation of solitary wave through the line. This paper is concluded in the last.
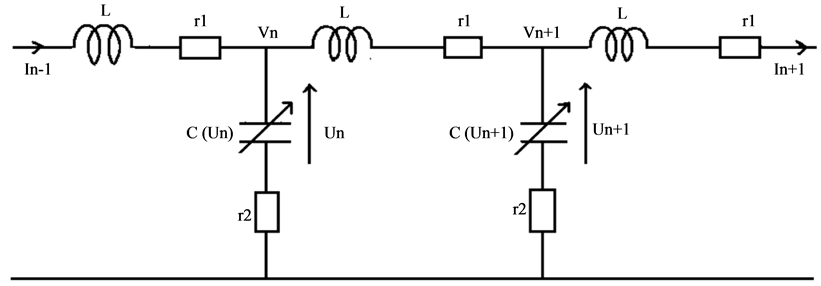
Figure 1. Schematic representation of the nonlinear electric line.
2. Model and Its Analytical Consideration
We consider a nonlinear transmission line which consists of a number of RLC blocks connected as illustrated in Figure 1. The capacitance-voltage relationship can be approximated by a second-order polynomial [1] [7] [9] [14] [17] [23] -[25]
 (1)
(1)
where C1 is a constant corresponding to the capacitance of the nonlinear diode at the dcbias-voltage U0. The nonlinear parameters 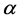 and
and  are assumed to be positive or negative constants.
are assumed to be positive or negative constants.  and
and 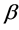 are nonlinear coefficients that determine electric charge Qn stored in the n-th capacitor in the line, and Un is the voltage across the n-th capacitor. For the diode the sign of
are nonlinear coefficients that determine electric charge Qn stored in the n-th capacitor in the line, and Un is the voltage across the n-th capacitor. For the diode the sign of  is negative and the sign of
is negative and the sign of  is positive and vice versa for the MOS. By applying the Kirchhoff’s laws to transmission line we obtain
is positive and vice versa for the MOS. By applying the Kirchhoff’s laws to transmission line we obtain
 (2)
(2)
Next, measuring time in units of 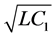 , we express Equation (2) in the following dimensionless form:
, we express Equation (2) in the following dimensionless form:
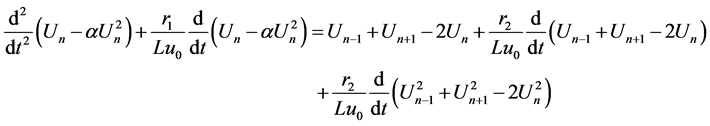 (3)
(3)
Starting from the semi-discrete model given by Equation (3), we develop a continuum model in the standard way, i.e. the right-hand side of (3) can be approximated with partial derivatives with respect to distance , from the beginning of the line, assuming that the spacing between two adjacent sections is
, from the beginning of the line, assuming that the spacing between two adjacent sections is  (This is spatial sampling period equals the length of each element). Therefore, an approximate continuous partial differential Equation (3) can be obtained by using the Taylor expansions of Un + 1(t) and Un − 1(t), both around the reference value Un(t). We regard the following equation as a continuum model of the transmission line that retains the effect of discreteness in the fourth-order term:
(This is spatial sampling period equals the length of each element). Therefore, an approximate continuous partial differential Equation (3) can be obtained by using the Taylor expansions of Un + 1(t) and Un − 1(t), both around the reference value Un(t). We regard the following equation as a continuum model of the transmission line that retains the effect of discreteness in the fourth-order term:
 (4)
(4)
Setting dimensionless voltage F, such that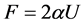 , after some extensive manipulations [26] , we obtain the equation describing the developing solitonic pulses:
, after some extensive manipulations [26] , we obtain the equation describing the developing solitonic pulses:
 (5)
(5)
with,  To derive the previous equation, we used within the perturbative method [27] the Gardner-Morikawa transformation that guarantees the balance between the nonlinearity and dispersion in series expansion as follows:
To derive the previous equation, we used within the perturbative method [27] the Gardner-Morikawa transformation that guarantees the balance between the nonlinearity and dispersion in series expansion as follows:
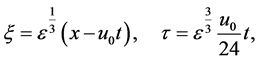 (6)
(6)
and a further transformation of constants and variables such as
 (7)
(7)
where  is an indicator of the slowness. Equation (5) governs the propagation of traveling on linear waves in the network. This equation is well known as the perturbed KdV equation. In particular, in the absence of dissipative terms (r1 = r2 = 0) it can support the well-known pulse soliton solution of the KdV (Korteweg-de Vries) equation. The KdV equation is the generic model for the study of weakly nonlinear long waves. It arises in physical systems which involve a balance between nonlinearity and dispersion at leading-order. For example, it describes surface waves of long wave length and small amplitude on shallow water and internal waves in a shallow density-stratified fluid. Many other applications for the KdV equations so exist, such as plasma waves, Ross waves and magma flow. Also, the KdV equation is integrable. This means that a collision between KdV solitary waves is elastic; after the collision the solitons retain their original shape with the only memory of the collision being a phase shift. The explicit solution for interacting KdV solitons was developed using the bilinear transformation method, by Hirota [2] . Which has a soliton solution explicitly described as
is an indicator of the slowness. Equation (5) governs the propagation of traveling on linear waves in the network. This equation is well known as the perturbed KdV equation. In particular, in the absence of dissipative terms (r1 = r2 = 0) it can support the well-known pulse soliton solution of the KdV (Korteweg-de Vries) equation. The KdV equation is the generic model for the study of weakly nonlinear long waves. It arises in physical systems which involve a balance between nonlinearity and dispersion at leading-order. For example, it describes surface waves of long wave length and small amplitude on shallow water and internal waves in a shallow density-stratified fluid. Many other applications for the KdV equations so exist, such as plasma waves, Ross waves and magma flow. Also, the KdV equation is integrable. This means that a collision between KdV solitary waves is elastic; after the collision the solitons retain their original shape with the only memory of the collision being a phase shift. The explicit solution for interacting KdV solitons was developed using the bilinear transformation method, by Hirota [2] . Which has a soliton solution explicitly described as
 (8)
(8)
In the case of finite  and
and 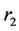 the exact solution of Equation (8) can no longer be obtained. However, in the framework of the perturbation theory as applied to KdV equation on the basis of the inverse scattering method [28] , a soliton-like pulse
the exact solution of Equation (8) can no longer be obtained. However, in the framework of the perturbation theory as applied to KdV equation on the basis of the inverse scattering method [28] , a soliton-like pulse
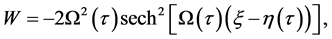 (9)
(9)
is obtained, where the quantity  and
and  obey the equations
obey the equations
 (10)
(10)
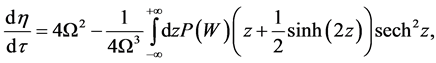 (11)
(11)
where  and
and 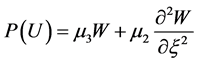
 (12)
(12)
where  and
and  corresponds to the unperturbed soliton’s amplitude. This shows that
corresponds to the unperturbed soliton’s amplitude. This shows that  decreases as
decreases as  increases.
increases.
Another particular case, when we set  and
and  Equation (8) is commonly called the Korteweg-de Vries-Burgers equation. This equation plays an important role in applications. In certain cases, the coefficient
Equation (8) is commonly called the Korteweg-de Vries-Burgers equation. This equation plays an important role in applications. In certain cases, the coefficient  in equation (8) may be negative. In those cases, the perturbed KdV equation describes the development of instability. For
in equation (8) may be negative. In those cases, the perturbed KdV equation describes the development of instability. For  and
and , perturbation describes a variable depth in shallow water theory;
, perturbation describes a variable depth in shallow water theory;  corresponds to a constant depth gradient. The KdV equation with
corresponds to a constant depth gradient. The KdV equation with  finds a similar application in the description of nonlinear ion acoustic waves in an inhomogeneous plasma [28] .
finds a similar application in the description of nonlinear ion acoustic waves in an inhomogeneous plasma [28] .
3. Numerical Investigations
In order to study the behavior of the soliton along the cascaded maps, we numerically solve Equation (3) using the fourth-order Runge-Kutta scheme with a normalized integration time step . The parameters of the line are: L = 470 μH, C1 = 320 pF. At the input of the line, we launch as initial solution the dark solution obtained above. Figure 2, Figure 3 and Figure 4 show the propagation of these solutions through the line.
. The parameters of the line are: L = 470 μH, C1 = 320 pF. At the input of the line, we launch as initial solution the dark solution obtained above. Figure 2, Figure 3 and Figure 4 show the propagation of these solutions through the line.

Figure 2. The pulse decay of an initial pulse V(n = 0) = ‒sech2(n − n0) at n0 = 25 cell and different times, with α = 0.21 V−1, r1 = 1 Ω; r2 = 0.1 Ω.

Figure 3. The pulse decay of an initial pulse V(n = 0) = −sech2(n−n0) at n0 = 25 cell and different times, with α = 0.21 V−1, r1 = 0.1 Ω; r2 = 1 Ω.
It can be seen that the soliton keep its shape when traveling down the line. Dark soliton appears as an intensity dip in an infinitely extended constant background. It has been investigated in many theoretical and experimental papers [29] [30] . The dark solitons have attracted much attention due to their potential applications [31] . For example, using structures created during the propagation and interaction of the dark solitons, many types of all-optical switches may be written [32] . Other applications of the dark solitons involve the optical logic devices [33] and waveguide optics as dynamic switches and junctions [34] . They are also considered in signal processing and communication because of their inherent stability [35] . Compared with the bright solitons, they have better stability against various perturbations such as fiber loss, mutual interaction between neighboring pulses, the Raman effect, and the superposition of noise emitted from optical amplifiers. These solutions are plotted for cell 25. Coherent structures and chaotic states are well known as two distinct states of nonlinear dissipative wave
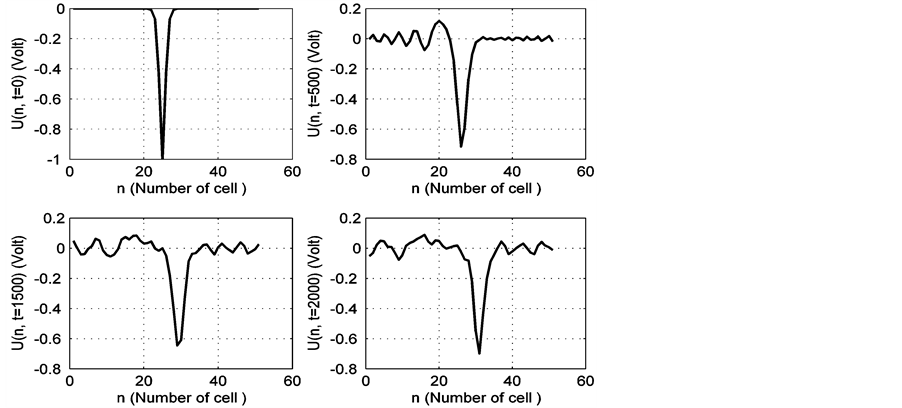
Figure 4. The pulse decay of an initial pulse V(n = 0) = −sech2(n − n0) at n0 = 25 cell and different times, with α = 0.21 V−1, r1 = 0 Ω; r2 = 0.0 Ω.
 (a)
(a)  (b)
(b)
Figure 5. The evolution of dark soliton solution of an initial pulse V(n = 0) = −sech2(n − n0) at n = 25 cell with α = 0.21 V−1, r1 = 1Ω; r2 = 0.1 Ω.
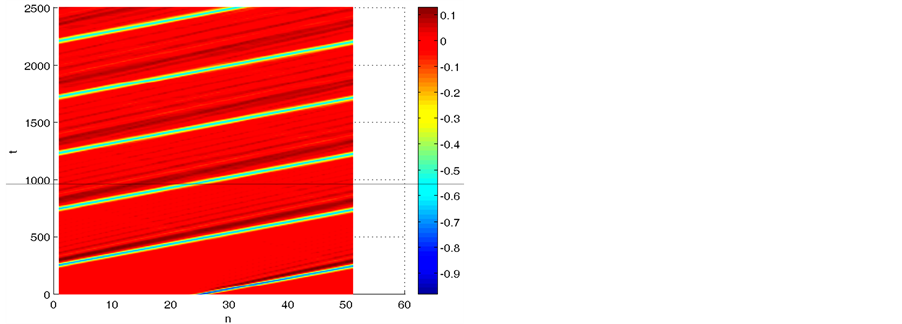 (a)
(a) (b)
(b)
Figure 6. The evolution of dark soliton solution of an initial pulse V(n = 0) = −sech2(n − n0) at n = 25 cell with α = 0.21 V−1, r1 = 0.1 Ω; r2 = 1 Ω.
 (a)
(a) (b)
(b)
Figure 7. The evolution of dark soliton solution of an initial pulse V(n = 0) = −sech2(n − n0) at n = 25 cell with α = 0.21 V−1, r1 = 0 Ω; r2 = 0 Ω.
systems. However, these states sometimes occur and propagate together in some systems. Figure 5, Figure 6, Figure 7 depict the incoherent evolution of dark solitons through the line. This incoherent evolution of dark soliton can also be evidenced from the nonreproducibility of experiments devoted to their propagation in the nonlinear medium, as observed by Ablowitz et al. [36] in the context of fluid dynamics that is, considering modulated periodic Stokes waves in deep water. For two different experiments with initial identical signals generated by the wave maker, the resulting temporal evolutions of the surface displacement at a given position in the tank are graphed against each other to produce a “phase plane” plot indicating the level of reproducibility.
4. Conclusion
In this paper, we have studied analytically and numerically dark soliton. These solutions have been also obtained in microtubules protein structure. We have used the nonlinear transmission line analog of this structure to derive a nonlinear lattice equation governing the voltage equation of the system. This lattice equation was then treated analytically, by means of the continuum medium approximation. The latter is a variant of the perturbation method, which takes into regard the discreteness of the system by considering the carrier (dark) wave as a discrete (continuum) object. This approach allowed us to derive, in the wavelength approximation, a nonlinear perturbed KdV equation. The KdV model was then used to predict the formation of dark soliton. Numerical simulations performed in the framework of the nonlinear lattice equation, with initial conditions borrowed from the exact KdV solution, revealed that the dark soliton propagated through the line. Furthermore, it was shown how certain physical parameters of the configuration may affect the results. We numerically found soliton profile and characteristics (amplitude and width) that are in very good agreement with the analytical predictions. Our study also shows the presence of chaos in the system.
Acknowledgements
S.Y.D. is very grateful for the support of the Higher Teachers’ Training College of Maroua through his Director, and to A. M and A. S.