Color Information Encoding Based on Phase-Truncated Gyrator Transform Domain ()
1. Introduction
Optical cryptography techniques have emerged as one of the next generation technologies, in which optical image encryption techniques have been widely studied because of their inherent advantages of high-speed and paralleloptical signal processing. Refregier and Javidi first proposed a double random phase encoding (DRPE) based on the 4-f optical correlator to encode an input image into stationary white noise [1] . Since then, various subsequent DRPE based optical encryption schemes have been introduced [2] -[6] . In all these image encryption techniques, as a monochromatic light is used to illuminate a real color image, color information is lost during decryption process. Since color images provide more information than gray scale images and also the additional color information contribute to a higher level of security. Zhang and Karim proposed a color encryption method based on an indexed image and DRPE [7] . The color image encryption techniques have been further extended [8] -[11] . However, the above proposed optical encryption techniques belong to the category of symmetric cryptosystems, in which the encryption keys are identical to the decryption keys. Qin and Peng proposed an asymmetric cryptosystem based on a phase-truncated Fourier transform (PTFT) to remove the linearity of the DRPE [12] . Recently, the PTFT-based encryption method has been found to be vulnerable to a specific attack based on iterative Fourier transforms, when the two random phase masks (RPMs) are used as public keys to encrypt different plaintexts [13] . The PTFT-based cryptosystem has been researched to resist against specific attack [14] -[16] .
In this paper, for the first time, to our knowledge, a new asymmetric color image cryptosystem based on gyrator transform (GT) domain is proposed. In this method, the color image is divided into R, G and B channels. Each of these channels is independently attached to the first RPM placed at the image plane and then gyrator transformed. The transformed image is phase-truncated to get first encoded image and amplitude-truncated to produce first decryption phase key. The transformed image is attached to the second RPM placed at the gyrator transform plane and then again gyrator transformed. The resulted image is phase-truncated to get second encoded image and amplitude-truncated to generate second decryption phase key. The proposed system provides transformation angles of GT as additional keys and decryption phase keys as asymmetric keys. Consequently, a high robustness against existing attacks can be achieved. Numerical simulations show the validity and viability of the proposed technique.
2. Gyrator Transform
The gyrator transform (GT) is defined as a linear canonical transform which produces the twisted rotation in position-spatial frequency planes of phase space. Thus, the GT operation of a two-dimensional function 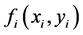 with parameter
with parameter , known as transformation angle, is defined as [17]
, known as transformation angle, is defined as [17]
 (1)
(1)
where 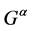 denotes gyrator transform operator,
denotes gyrator transform operator,  and
and  are the input and output coordinates, respectively. The GT can be realized by an optimized flexible optical system having plano-convex cylindrical lenses. The angle parameter
are the input and output coordinates, respectively. The GT can be realized by an optimized flexible optical system having plano-convex cylindrical lenses. The angle parameter  is changed by the proper rotation of these lenses [18] . Recently, the gyrator transformbased security systems for gray image [19] [20] and color image [11] [15] [16] have been extensively studied.
is changed by the proper rotation of these lenses [18] . Recently, the gyrator transformbased security systems for gray image [19] [20] and color image [11] [15] [16] have been extensively studied.
3. Proposed Method
In this method, an original color image is segregated into R, G and B color components. For simplicity, only red component is considered for the proposed cryptosystem. Let 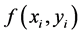 be original color image.
be original color image. ,
,  and
and  be its red, green and blue components, respectively. For simplicity, only red channel is illustrated. The subscript r has been used for red component. Let
be its red, green and blue components, respectively. For simplicity, only red channel is illustrated. The subscript r has been used for red component. Let  and
and 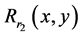 be independent random phase masks at input and transform planes, respectively. The RPM
be independent random phase masks at input and transform planes, respectively. The RPM  multiplied by
multiplied by  is gyrator transformed at rotation angles
is gyrator transformed at rotation angles  and then phase truncated to obtain encoded image
and then phase truncated to obtain encoded image . The resulted image
. The resulted image  multiplied by
multiplied by  is gyrator transformed at rotation
is gyrator transformed at rotation  and then phase truncated to get final encoded image
and then phase truncated to get final encoded image  [12] .
[12] .
 (2)
(2)
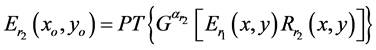 (3)
(3)
The operator  denotes phase truncation. Similarly, the amplitudes truncations of both
denotes phase truncation. Similarly, the amplitudes truncations of both 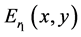 and
and  generate first and second asymmetric phase keys.
generate first and second asymmetric phase keys.
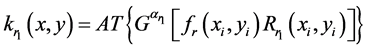 (4)
(4)
 (5)
(5)
where  indicates the operator of amplitude truncation.
indicates the operator of amplitude truncation.
The decryption process is straightforward and much simpler compared with encryption process.
 (6)
(6)
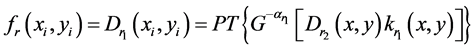 (7)
(7)
The blue and green channels are encrypted and decrypted by the same procedure.
The encryption process is performed digitally whereas the decryption process can be implemented using optoelectronic device. The GT can be implemented by using three generalized lenses (indicated as ,
,  and
and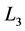 ) with fixed equal distances
) with fixed equal distances  between them. Each generalized lens corresponds to the combination of two identical plano-convex cylindrical lenses of the same power. The first and third identical generalized lenses of focal length
between them. Each generalized lens corresponds to the combination of two identical plano-convex cylindrical lenses of the same power. The first and third identical generalized lenses of focal length 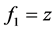 are rotated with respect to each other. The second generalized lens of a focal length
are rotated with respect to each other. The second generalized lens of a focal length  is fixed. These lenses are properly rotated to vary the transformation angle
is fixed. These lenses are properly rotated to vary the transformation angle  [18] .
[18] .
The optical setup is shown in Figure 1 & Figure 2. For convenience, only the red channel is considered. The encrypted red-channel  is multiplied with decryption phase key
is multiplied with decryption phase key , displayed on first Spatial Light Modulator (SLM), illuminated by a collimated beam and then optically transformed by first GT. The intensity of image recorded by a CCD 1 camera. Now the transformed image is multiplied with decryption phase key
, displayed on first Spatial Light Modulator (SLM), illuminated by a collimated beam and then optically transformed by first GT. The intensity of image recorded by a CCD 1 camera. Now the transformed image is multiplied with decryption phase key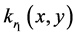 , displayed on the second SLM, illuminated by the collimated beam and then optically transformed by second GT. The intensity of image is recorded by the CCD 2 camera. The same process is repeated with encrypted greenand blue-channels to obtain corresponding green and blue channels. Finally, the decrypted color channels are combined into decrypted color image by using a computer system.
, displayed on the second SLM, illuminated by the collimated beam and then optically transformed by second GT. The intensity of image is recorded by the CCD 2 camera. The same process is repeated with encrypted greenand blue-channels to obtain corresponding green and blue channels. Finally, the decrypted color channels are combined into decrypted color image by using a computer system.

Figure 1. Optical setup for proposed color image decryption system.
 (a)
(a) (b)
(b)
Figure 2. Simulation results of the proposed method: (a) Original color image with 512 × 512 pixels to be encoded; (b) encrypted image with all correct keys (c) real part of the first decryption phase key; (d) real part of the second decryption phase key; (e) retrieved image with arbitrary phase key; (f) recovered image with no phase keys; (g) reconstructed image with the transformation angle for each channel changed by 0.3 but all the other parameters are correct; (h) decrypted image with all right keys.
4. Numerical Simulation Results
Numerical simulations have been carried out on a Matlab 7.11.0 (R2010b) platform to test the feasibility and security of the new proposal. The original color image having size  pixels is shown in Figure 2(a). The first and second transformation angles of the GT for red, green and blue channels are, respectively,
pixels is shown in Figure 2(a). The first and second transformation angles of the GT for red, green and blue channels are, respectively, 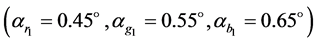 and
and . The encrypted image produced by three-multiplexed channels is shown in Figure 2(b). The real parts of three-multiplexed channels of first and second asymmetric phase keys are, respectively, illustrated in Figure 2(c) and Figure 2(d). The retrieved images with arbitrary phase key and with no phase keys are demonstrated in Figure 2(e) and Figure 1(f), respectively. The recovered images with the transformation angle for each channel changed by
. The encrypted image produced by three-multiplexed channels is shown in Figure 2(b). The real parts of three-multiplexed channels of first and second asymmetric phase keys are, respectively, illustrated in Figure 2(c) and Figure 2(d). The retrieved images with arbitrary phase key and with no phase keys are demonstrated in Figure 2(e) and Figure 1(f), respectively. The recovered images with the transformation angle for each channel changed by 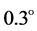 and with all correct keys are demonstrated in Figure 2(g) and Figure 2(h), respectively. As can be seen from Figures 2(e)-(g), corresponding decrypted images provide no valuable information about the original color image. That means the original image can only be obtained if all the decryption keys are accurate as shown in Figure 2(h).
and with all correct keys are demonstrated in Figure 2(g) and Figure 2(h), respectively. As can be seen from Figures 2(e)-(g), corresponding decrypted images provide no valuable information about the original color image. That means the original image can only be obtained if all the decryption keys are accurate as shown in Figure 2(h).
To evaluate the reliability of the proposed algorithm quantitatively, the mean square error (MSE) is introduced and defined as
 (8)
(8)
where  and
and 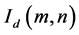 indicate the original and decrypted image at pixel position
indicate the original and decrypted image at pixel position , respectively.
, respectively. 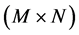 represents the size of the image.
represents the size of the image.
In Figure 2(b), the MSE values of encrypted result with all the correct keys are  for red, green and blue channels, respectively. These values are very high, which indicate that no information about the original image can be obtained. The calculated MSE values corresponding to Figure 2(e) and Figure 2(f) for red, green and blue channels are
for red, green and blue channels, respectively. These values are very high, which indicate that no information about the original image can be obtained. The calculated MSE values corresponding to Figure 2(e) and Figure 2(f) for red, green and blue channels are  and
and , respectively. The high MSE values, for arbitrary phase key and no phase keys, sufficiently reveal the strength of the proposed algorithm. The MSE values for a very small error of
, respectively. The high MSE values, for arbitrary phase key and no phase keys, sufficiently reveal the strength of the proposed algorithm. The MSE values for a very small error of  in transformation angle of GT for red, green and blue is
in transformation angle of GT for red, green and blue is . The high MSE results adequately demonstrate the robustness of the proposed system.
. The high MSE results adequately demonstrate the robustness of the proposed system.
In attack analysis, first the known plaintext attack is considered, in which an attacker knows all the transformation angles and attempts to produce decryption keys from a fake color image of size  pixels as shown Figure 3(a); the real parts of the first fake decryption key and second fake decryption key are displayed in Figure 3(b) and Figure 3(c). The decrypted image with all fake keys with correct transformation angles is illustrated in Figures 3(d). That means an unauthorized user can not retrieve the original image. So, the proposed technique can resist against brute force attack.
pixels as shown Figure 3(a); the real parts of the first fake decryption key and second fake decryption key are displayed in Figure 3(b) and Figure 3(c). The decrypted image with all fake keys with correct transformation angles is illustrated in Figures 3(d). That means an unauthorized user can not retrieve the original image. So, the proposed technique can resist against brute force attack.
Second, the robustness of the proposed technique against occlusion attacks on the encrypted data has been examined. The 50%- and 70%- occluded encrypted images are shown in Figure 4(a) and Figure 4(c), respectively. The calculated MSE values corresponding to recovered images with all correct keys as displayed in Figure 4(b) and Figure 4(d) for red, green and blue channels, are 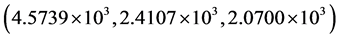 and
and , respectively.
, respectively.
Third, the robustness of the proposed method against noise attacks on the encrypted data has also been checked. The Gaussian and speckle noised encrypted images with variance 0.1 are displayed in Figure 5(a) and Figure 5(c), respectively. The resulted MSE values corresponding to retrieved images with all right keys as depicted in Figure 5(b) and Figure 5(d) for red, green and blue channels, are 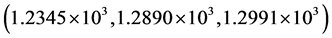 and
and , respectively.
, respectively.
From above results, it can be concluded that if the encrypted data is destroyed by occlusion or degraded by noise in storage and transmission process, the decrypted image with all right keys is recognizable. Therefore, the proposed method has certain robustness against occlusion and noise attacks.
The sensitive degree of the transformation angle is analyzed and then calculated. The sampling interval is fixed at the range , sampling length is taken at 0.01 and other decryption keys are used with correct values. The corresponding MSE curves between original red, green and blue channels and their corresponding decrypted images are depicted in Figures 6(a)-(c). These MSE curves have very narrow downward peaks. The MSE of red channel is quite sensitive as compared to green and blue channels. The value of MSE function becomes zero at
, sampling length is taken at 0.01 and other decryption keys are used with correct values. The corresponding MSE curves between original red, green and blue channels and their corresponding decrypted images are depicted in Figures 6(a)-(c). These MSE curves have very narrow downward peaks. The MSE of red channel is quite sensitive as compared to green and blue channels. The value of MSE function becomes zero at 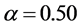 with correct decryption keys. The zero-MSE value indicates that the original image is decrypted completely.
with correct decryption keys. The zero-MSE value indicates that the original image is decrypted completely.
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 3. Known plaintext attack: (a) Fake color image with 512×512 pixels; (b) real part of the first fake decryption key; (c) real part of the second fake decryption key; (d) retrieved image with all fake keys with correct transformation angles.
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 4. Test of occlusion attack: (a) encoded image with 50% occlusion; (b) corresponding reconstructed image image with all accurate keys; (c) encoded image with 75% occlusion; (d) corresponding reconstructed image with all exact keys.
 (a) (b) (c) (d)
(a) (b) (c) (d)
Figure 5. Test of noise attack: (a) encoded image having Gaussian noise with variance 0.1; (b) corresponding decrypted image with all correct keys (c) encoded image having speckle noise with variance 0.1; (d) corresponding retrieved image with all right keys.
 (a)
(a)  (b)
(b)  (c)
(c)
Figure 6. (a) MSE versus variation in transformation angle for red channel; (b) MSE versus variation in transformation angle for green channel; and (c) MSE versus variation in transformation angle for blue channel.
5. Conclusion
A new information encryption system based phase-truncated gyrator transform domain is presented. The original color image is separated into 
 and
and  channels. The separated three RBG channels avoid the interference of crosstalks efficiently. The two random phase masks are encryption keys which are used as public keys. The two asymmetric phase keys are decryption keys which are employed as private keys. That means only authorized users can decrypt the original information. The transformation angles of GT as supplementary keys significantly enhance the security of the proposed system. The numerical simulations have shown the effectiveness of this method.
channels. The separated three RBG channels avoid the interference of crosstalks efficiently. The two random phase masks are encryption keys which are used as public keys. The two asymmetric phase keys are decryption keys which are employed as private keys. That means only authorized users can decrypt the original information. The transformation angles of GT as supplementary keys significantly enhance the security of the proposed system. The numerical simulations have shown the effectiveness of this method.
NOTES
*Corresponding author.